“用相似三角形解決問題2”教學設計
劉學俊

《2011版初中數學課程標準》明確提出:將數學作為一門“承載教育使命的課程”,導致“作為教育任務的數學”具備了諸多有別于數學科學的特征.這樣的數學是“為學生準備的數學”——無論是需要學習的主題,還是用于展開學習的素材.這就為我們教師的教學設計提供了更廣闊的思路,恰好筆者在教學“用相似三角形解決問題2”時,依據這一理念進行了巧妙設計,效果很好!
一、從學生興趣出發,準備問題情境
以春晚節目《逗趣》中的手影戲剪輯為情境,激發學生興趣,引入課題.
二、從學生認知層次出發,準備探索新知的流程
1.中心投影的意義.(在學生聯系實際后直接下定義:像這樣,在點光源的照射下,物體所產生的影稱為中心投影.學生很容易接受)
2.中心投影中影子和光源的確定.(已知光源會畫影子和根據影子找出光源是學生必須掌握的,也是對現行教材的內容補充.這兒學生容易理解,只是老師需要強調一下規范作圖的要求.因此我設計了兩個層次的活動:一個是基本作圖,一個是綜合運用,如圖所示)
(1)請畫出圖中雙胞胎姐妹在路燈下的影子,請確定圖中路燈燈泡所在的位置.
(2)一天晚飯后,姐姐小麗帶著弟弟小剛出去散步,經過一盞路燈時,小剛突然高興地對姐姐說:“我踩到你的‘腦袋了.”你能確定小剛此時所站的位置嗎?如果此時小剛的影子與姐姐小麗的影子一樣長,你能在圖中畫出表示小剛身高的線段嗎?
3.正確區分中心投影與平行投影.(在此我設計了兩個內容:一是數學實驗室,即對比平行投影的性質探索在中心投影下物高和影長的關系;二是在此基礎上小結一下平行投影與中心投影的異同)
(1)取兩個長度相等的小木棒,將它們直立擺放在不同的位置,固定光源,測量木棒的影長.它們的影長相等嗎?
(2)改變光源的位置,木棒的影長發生了什么變化?
(3)改變小木棒的高度,木棒的影長發生了變化嗎?
(4)如圖的影子是在太陽光下形成的還是在燈光下形成的?(在學生判斷之前,老師要求他們先小結中心投影與平行投影的異同,這時學生的方法可能不太一樣,教師再加以引導)
三、從學生核心思維的提升出發,設計實際運用問題
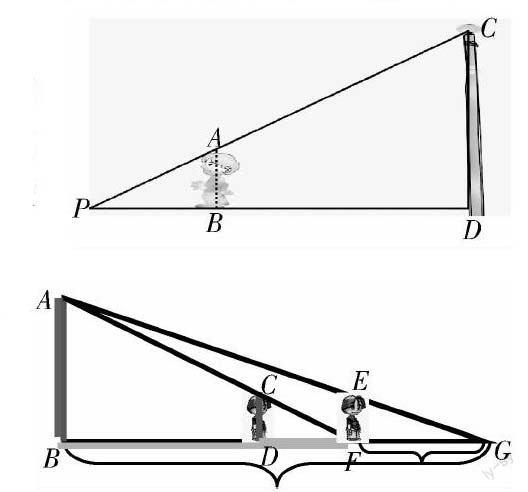
問題:某同學身高AB=1.60 m,他從路燈桿底部的點D沿直線前進4 m到點B,此時其影長PB=2 m.求路燈桿CD的高度.
變式:河對岸有一根路燈桿AB,在燈光下,小明在點D處測得自己的影長DF=3 m,沿BD方向到達點F處再測得自己的影長FG=4 m.如果小明的身高為1.6 m,求路燈桿AB的高度.
四、思維拓展
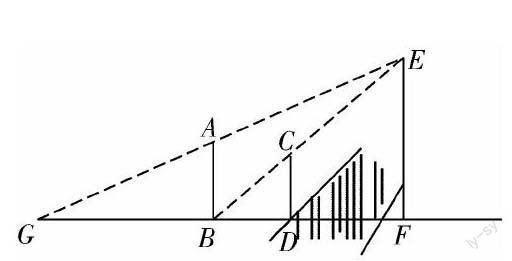
如圖,有兩根直立于地面的電線桿AB,CD,其中CD在河邊上,且AB=10 m,CD=8 m.河對岸有一高桿路燈EF,它的著地點F與兩電線桿的著地點B,D在同一直線上.在強燈光照射下,電線桿CD的影子的頂端恰好與電線桿AB的底部(B)重合.今測得影子DB=10 m,電線桿AB的影子BG=25 m.求路燈燈桿的高度(EF)與河的寬度(DF).
五、課堂小結:通過本節課的學習,你有哪些收獲?
1.中心投影的意義;
2.如何正確區分中心投影和平行投影;
3.綜合運用判定三角形相似的條件和三角形相似的性質解決問題.
六、預設和設計反思
本節課立足從學生熟悉的生活情境——燈光下的手影引起學生的共鳴,從而聯想到他們的實際體會;其次再通過實際操作探索中心投影的含義,對比平行投影加以區別;最后通過尋找相似三角形來解決實際問題,問題的難度一個比一個加深,意在不斷提升學生的思維層次.真正從“為學生準備的數學”出發,數學來源于生活,但又高于生活,有思維含量的提升!

