基于倒頻譜的無噪聲運動模糊圖像快速復原算法

魏　鑫，陳廣鋒

(東華大學 紡織裝備教育部工程研究中心， 上海 201620)

基于倒頻譜的無噪聲運動模糊圖像快速復原算法

魏鑫，陳廣鋒

(東華大學 紡織裝備教育部工程研究中心， 上海 201620)

摘要：針對當前運動模糊圖像復原算法主要集中在非實時性研究，著重考慮算法的執行質量而不考慮算法執行效率的問題，提出了基于倒頻譜的無噪聲圖像的快速復原算法.該算法對無噪聲模糊圖像進行倒頻譜處理，從倒頻譜圖中直接得到圖像的模糊方向和模糊距離.對于尺寸較大的圖像，在執行倒頻譜算法前先使用雙線性插值算法實現圖像壓縮，再進行倒頻譜操作.通過比較各種復原算法的執行效率及效果，采用維納濾波對圖像進行復原.通過對多幅模糊圖像進行仿真復原試驗，在獲得了良好的復原效果的同時也取得了較高的執行效率.

關鍵詞：運動模糊； 雙線性插值； 倒頻譜； 維納濾波； 圖像復原

成像器件對目標成像時，在曝光時間內感光介質與被照物影像間存在相對運動而帶來的成像模糊稱為運動模糊[1].對傳送帶上的工件進行表面缺陷檢測時，得到的必然是具有運動模糊特性的圖像.

運動模糊圖像復原已得到廣泛的重視和研究，并且國內外研究提出的各種復原方法已經取得了一定的成效[2].運動模糊圖像的退化模型中使用最廣泛的為點擴散模型，眾多研究者研究了很多獲取點擴散函數(PSF)參數的方法.有的方法通過鑒別曲線來求圖像運動模糊的長度，即將微分自相關圖像各列實施求和，得到一條鑒別曲線，曲線上會出現一對共軛的相關峰，這對相關峰對稱分布在零頻尖峰兩側，鑒別出這兩個相關峰的位置，就可以得出運動模糊點擴散函數的尺度[3].文獻[1]中使用倒頻譜和Radon(隨機)變化的方法確定了PSF參數.文獻[3]利用測量傅里葉譜中黑帶間隔距離確定模糊長度，使用圖像灰度值方向微分確定模糊方向.文獻[7]中使用Garbor濾波器和模糊圖像的傅里葉譜進行卷積，通過比較不同方向的響應來得到模糊角度，使用徑向基函數神經網絡(RBFNN)確定模糊長度.文獻[8-9]提出了通過計算模糊圖像梯度的功率譜來獲得頻域內明暗相間的線條，計算線條間的距離和線條方向來獲取PSF參數，本質上與其他方法無區別.文獻[10]所提出的圖像去模糊方法的創新之處在于圖像復原部分使用了基于全變分的復原算法，該算法對于運動模糊和離焦模糊情況均有很好的復原效果，但效率較低，256像素×256像素的Cameraman圖像需要使用1.7 s才能實現圖像的復原.以上算法都試圖成為通用算法，考慮的因素較多，造成算法的效率低下.雖有文獻[10]研究了快速復原算法，但這種快速是相比其他算法的，并不是絕對的快速，即不適用于傳送帶上圖像的實時復原.

在專門用于傳送帶的影像測量系統中，模糊圖像中很少存在噪聲影響，但對算法的效率要求高.本文針對這種特殊需求，綜合考慮常見壓縮算法的優缺點，提出了先使用雙線性插值算法對圖像進行壓縮，保證了圖像的信息熵不會過度減小，再使用倒頻譜法獲取PSF參數，最后比較各種復原算法的執行效率和效果，選擇最符合實時在線測量系統的復原算法.

1圖像壓縮

用于實時在線檢測的工業相機像素往往不高，但一般也有100萬像素.這樣的相機拍出來的圖像尺寸也較大，增大了算法的計算量，延長了計算時間，因此在倒頻譜前需要對圖像進行壓縮處理.

1.1常見壓縮算法分析

常見的圖像壓縮算法有霍夫曼編碼、離散余弦變換(DCT)、小波壓縮和雙線性插值算法等.前兩種壓縮算法僅改變圖像的編碼冗余，圖像尺寸并不下降，不僅無法減少后續算法的計算量，而且由于圖像質量下降，導致圖像的信噪比降低，反而影響倒頻譜算法的準確度.而小波圖像壓縮的特點在于壓縮比高、壓縮速度快，壓縮后能保持信號與圖像的基本特征不變[4].但是小波壓縮時相當于對原圖添加了低通濾波器，同時對原圖做“下二采樣”(即序列僅保留下標為偶數的元素)，因此，經過小波壓縮的圖像必然丟失了原圖中的高頻信息.

1.2雙線性插值算法

在圖像的雙線性插值算法中，目標圖像中新創造的像素值，是由源圖像位置在它附近2×2區域的4個臨近像素的值通過加權平均計算得出的.此算法也具有低通濾波器的性質，使高頻分量受損，可能使圖像輪廓變得模糊.雙線性插值示意圖如圖1所示.

圖1　雙線性插值示意圖Fig.1　Bilinear interpolation schematic

如圖1所示，x軸方向的線性插值為

(1)

其中：R1=(x,y1).

(2)

其中：R2=(x,y2).

y軸方向的線性插值為

(3)

由于雙線性插值算法綜合考慮了臨近像素的影響，對高頻分量的過濾較少，且算法直接在空域操作，因此，算法壓縮效果較好，執行效率較高.

1.3兩種壓縮算法下圖像質量及壓縮效率對比

由于壓縮后的圖像尺寸已經改變，因此，均方誤差、峰值信噪比等全參考質量評價方法不適用.本文使用信息熵對小波壓縮和雙線性插值這兩種算法壓縮后的模糊圖像質量進行評價.圖2為接插件殼體的模糊圖及其分別經小波壓縮和雙線性插值后得到的壓縮圖像.

(a) 模糊原圖

(b) 小波壓縮圖

(c) 雙線性插值壓縮圖

從圖2中很難直觀發現兩種壓縮算法所得圖像質量的區別，不同壓縮算法的壓縮效率及效果對比如表1所示.由表1中的數據可看出，雙線性插值算法較小波壓縮算法在效率上有了很顯著的提高. 從圖像質量角度來說，相比于雙線性插值算法，小波壓縮算法處理后的信息熵增大更多，即圖像質量下降更為劇烈.對兩種壓縮算法執行過程分析可知，因小波壓縮算法中存在“下二采樣”操作，破壞了原圖像的連續性，導致圖像信息熵增大，圖像質量下降；雙線性插值算法相當于對圖像進行了低通濾波操作，因此圖像被輕微模糊，信息熵略有下降.鑒于雙線性插值算法的執行效率高，以及壓縮后圖像質量下降較少的優點，本文在執行后續倒頻譜和復原算法前使用該算法進行圖像壓縮.

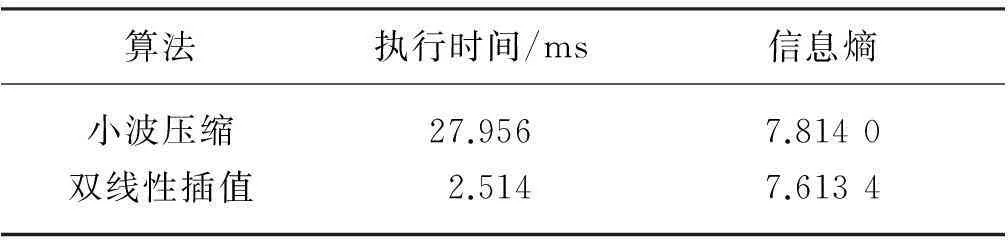
表1　不同壓縮算法的壓縮效率及效果對比

注：未模糊圖像信息熵為7.5954，模糊未壓縮圖像信息熵為7.6206， 尺寸為816像素×219像素.

2圖像的退化和復原

2.1圖像的退化和復原模型

圖像的運動模糊過程可以被模型化為一個退化函數和一個加性噪聲項[1].輸入圖像f(x,y)，得到退化圖像g(x,y).假設H是一個線性、位置不變性的過程，空間域給出的退化圖像可由式(4)給出.

g(x,y)=h(x,y)*f(x,y)+n(x,y)

(4)

其中：h(x,y)為退化函數的空間描述；*為空間卷積.對應頻域下的描述為

G(u,v)=H(u,v)F(u,v)+N(u,v)

(5)

其中：大寫字母項為式(1)中相應項的傅里葉變換.因為本文并不考慮噪聲的影響，故式(5)中N(u,v)=0. 圖3為圖像的退化和復原過程圖.

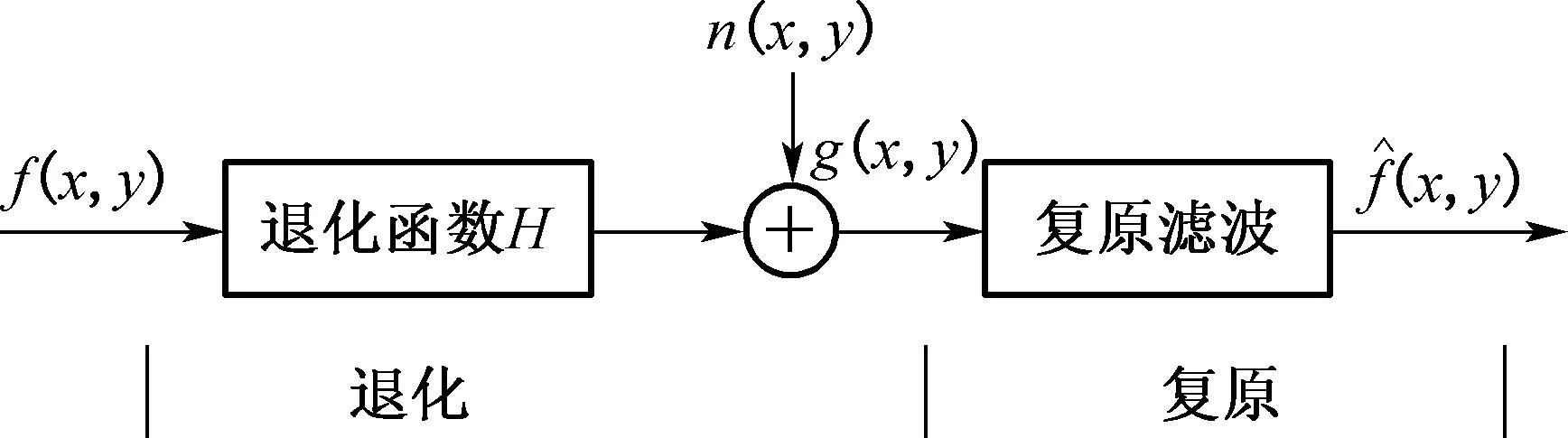
圖3　圖像的退化和復原過程Fig.3　Image degradation and restoration processes

2.2勻速直線運動退化模型

在圖像采集過程中被拍攝物和攝像機之間的相對運動會造成圖像的模糊.假設T表示曝光時間，f(x,y)表示勻速直線運動的物體，g(x,y)表示運動模糊產生的退化圖像，x0(t)和y0(t)分別表示物體在x軸和y軸方向上運動時的變化分量，勻速直線運動模糊圖像的退化模型可以表示為

(6)

對式(6)進行傅里葉變化后并整理，可得

(7)

對比式(5)和(7)可知，

(8)

式(8)即為任意方向勻速直線運動模糊圖像退化模型的傳遞函數.

3倒頻譜法鑒定模糊參數

3.1倒頻譜定義及意義分析

倒頻譜最初定義來自文獻[5]，定義為

Cg(p,q)=F-1[log10|G(u,v)|]

(9)

參閱文獻[1-2]，倒頻譜可表示為

8．宋高似孫《夜宿金庭洞》：“夙聞桐柏山，下有金庭洞；五云所出沒，千翠相迎送；川明芝自燁，夏冷雪猶凍；沙泉涇陽水，蒼碧孕陰峒；天光抱瓊臺，神力扶蘭棟；其左聞蒼蚪，其西翔紫鳳……”[14]

Cg(p,q)=Cf(p,q)+Ch(p,q)

(10)

其中：Cf(p,q)為原始圖像倒頻譜；Ch(p,q)為點擴散函數倒頻譜.

圖2中各圖所對應的倒頻譜圖如圖4所示，其模糊角度為60°，模糊距離為20像素.

(a) 原圖倒譜圖

(b) 小波壓縮圖倒譜圖

(c) 雙線性插值壓縮圖倒譜圖

圖4中的亮點對應于原圖中的低頻分量，亮線的方向就對應于原圖中的低頻方向.對于運動模糊圖像，模糊方向上的像素處于低頻，垂直于模糊方向則對應圖像的高頻部分.因此對應圖4中各圖，60°方向有條很明顯的亮線.不同之處在于，圖4(a)中沒有其他方向的亮線，圖4(b)有很明顯的水平和垂直方向的亮線，圖4(c)中有微弱的水平和垂直方向的亮點.其原因在于：在圖4(b)中，原圖的中的高頻部分經小波壓縮后被剔除，模糊方向上低頻的主導優勢被弱化，其他方向上的低頻得以顯示；而雙線性插值算法也有低通濾波器的效果，故圖4(c)的原圖也被稍微模糊，導致其水平方向出現亮點.

3.2模糊參數獲取及精度比較

在圖4(a)和4(c)中，可以直接找到倒譜中的最小值點(有兩個)，兩點的連線方向即為運動模糊方向，兩點連線的距離為模糊長度的兩倍.而圖4(b)受水平、垂直方向亮點的影響，無法直接通過找最小值點來得到模糊參數.文獻[2]使用了Canny算子和灰度形態學來確定兩個最小值點的位置，顯然效率低下.

在不同模糊方向(α)及模糊長度(L)的條件下，先使用雙線性插值算法壓縮圖像，再使用倒頻譜得到的PSF參數，結果如表2所示.

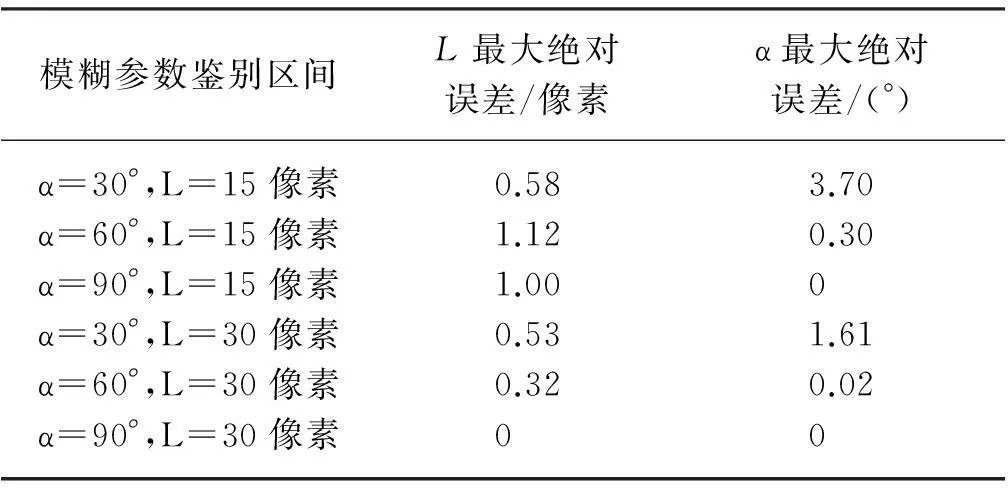
表2　不同測試條件的鑒別結果精度比較

本文雖然討論的是無噪聲運動模糊圖像的復原，但是從對圖4的分析中還可以得到以下結論，即當添加一定程度的高斯噪聲時，用倒頻譜法仍可以準確計算出PSF參數.高斯噪聲在圖像中屬于高頻，會影響原圖的低頻部分，故在倒頻譜圖中不會顯現，但卻縮短了倒頻譜圖的亮線.當圖像噪聲強度一定時，原圖中運動模糊方向的低頻仍占主導地位，倒頻譜中仍有亮線.噪聲強度再大時，低頻部分也被噪聲淹沒，倒頻譜圖上只有最中心的一個亮點，從而無法判定PSF參數.

對接插件殼體的模糊圖的添加均值為0和方差為0.001的高斯噪聲，再用本文的方法計算PSF參數，計算出模糊角度為60.945°，模糊長度為20.61像素，其倒頻譜圖如圖5所示.對比圖4(c)和5可發現，圖5中亮線的長度明顯縮短.

圖5　添加高斯噪聲的倒頻譜圖Fig.5　Cepstrum with Gaussian noise added

4運動模糊圖像復原試驗

經典的圖像復原算法有逆濾波、維納濾波、規則化濾波和Richardson-Lucy濾波.逆濾波復原要求模糊圖像的信噪比高，規則化濾波要求對原始圖像和噪聲的一些統計特性有先驗知識，Richardson-Lucy濾波雖是目前應用最廣泛的非線性迭代圖像復原技術，但多次迭代造成算法效率下降.綜合圖像復原質量和效率，本文選擇維納濾波.

4.1仿真運動模糊圖像復原

圖6為接插件殼體的原圖(816像素×219像素)、模糊圖、未壓縮復原圖和壓縮后復原圖的對比，其模糊角度為60°，模糊長度為20像素.

(a) 原圖

(b) 模糊圖

(c) 未壓縮復原圖

(d) 壓縮后復原圖

圖7為Cameraman的原圖(256像素×256像素)、模糊圖、未壓縮復原圖和壓縮后復原圖的對比，其模糊角度為60°，模糊長度為20像素.

(a) 原圖

(b) 模糊圖

(c) 未壓縮復原圖

d) 壓縮后復原圖

4.2實際模糊圖像復原

圖8和9分別為流水線上不同時刻工件的實拍圖(696像素×514像素)和壓縮后復原圖對比，分別為試驗3和4，且圖8測得模糊角度為90°，模糊長度為10像素，圖9測得模糊角度為92.71°，模糊長度為10.05像素.

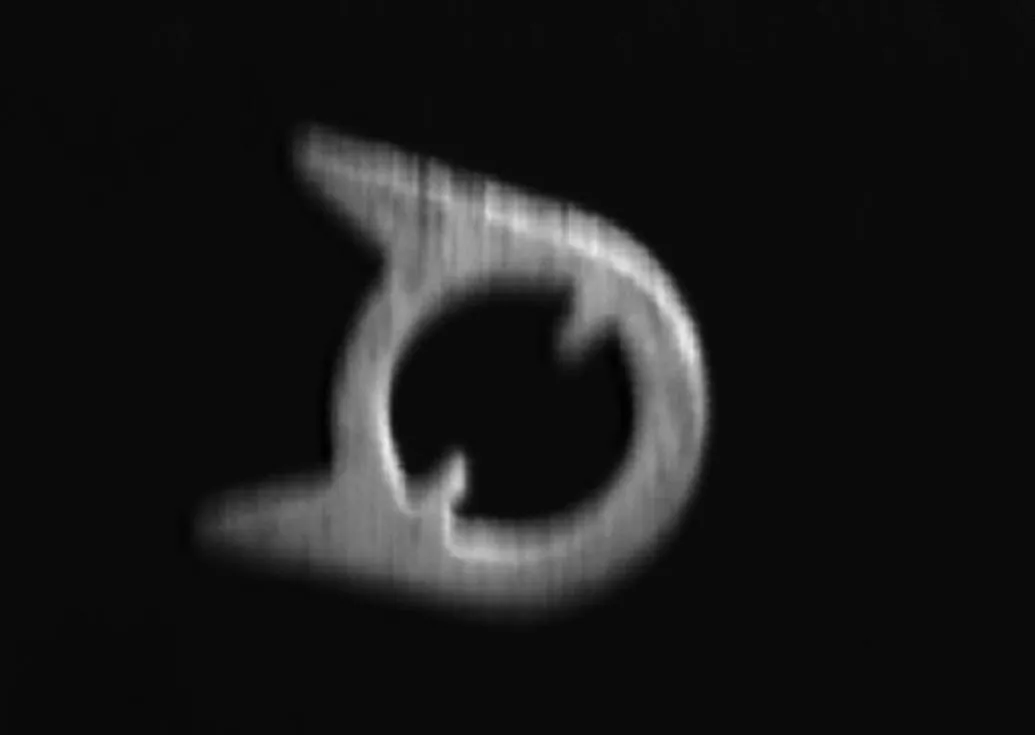
(a) 實拍圖

(b) 復原圖

(a) 實拍圖

(b) 復原圖

表3分別計算了4組試驗的復原效率和復原后圖像的信息熵.其中算法執行時間包括雙線性插值算法壓縮圖像時間、壓縮圖像倒頻譜并獲得的PSF參數時間和維納濾波復原時間.以試驗4為例，本文算法3部分的執行時間分別為1.8，6.5和9.4ms，如若未執行圖像壓縮，3部分的執行時間分別為0，26.1和37.5ms.由此可見，模糊圖像復原的執行時間主要花費在復原算法上.

表3　不同試驗的效率和效果對比

在不使用壓縮算法的情況下，文獻[1-3,5,7-9]中獲取PSF參數的方式一般包括傅里葉變化、濾波和形態學處理，它們的處理步驟均要多于本文的倒頻譜后取最小值法的處理步驟.由于雙線性插值屬于計算機擅長的線性運算，在保證圖像質量的情況下將圖像的大小壓縮至原來的1/4只需很短的時間，但后續操作的效率可以提高4倍.文獻[10]提出的快速復原算法的快速性是相對其他非線性復原方法的，雖然復原效果較好，但在模糊類型已知且不考慮噪聲的情況下，效率遠不及維納濾波復原.綜上所述，本文方法在獲取PSF參數和復原時都有更高的執行效率.

5結語

不同于以往只重視運動模糊圖像復原效果的研究，本文提出了先對模糊圖像進行雙線性插值壓縮，再經倒頻譜處理后快速地得到PSF參數，最后利用維納濾波對圖像進行復原的算法.該算法具有快速性和一定的抗噪聲能力，對比試驗的結果也表明算法具有良好的復原效果.本文試驗得到的執行時間是在Matlab中直接得到的，并未使用編譯后的函數，因此，如果使用OpenCV進行相同的操作，算法會更加高效，可以滿足實時在線復原的應用需求.

參考文獻

[1] 謝飛，車宏，蔡猛. 一種基于倒頻譜鑒別模糊參數的圖像復原算法[J]. 電光與控制，2011，18(7)：49-54.

[2] 王鵬飛. 運動模糊圖像復原算法研究[D]. 重慶：重慶大學光電工程學院，2013：2.

[3] 鄭輝. 運動模糊圖像復原技術的研究與實現[D]. 長沙：國防科學技術大學計算機學院，2007：16-19.

[4] 張德豐. Matlab數字圖像處理[M]. 2版. 北京：機械工業出版社，2013：253-254.

[5] ROM R. On the cepstrum of two-dimensional functions(Corresp)[J]. IEEE Transactions on Information Theory，1975，21(2)：214-217.

[6] GONZALEZRC， WOODSR E. Digital image processing[M]. 3版. 北京：電子工業出版社，2013：515-523.

[7] DASHR， MAJHIB. Motion blur parameters estimation for image restoration[J]. Optik，2014，125：1634-1640.

[8] GOVINDAN S， SARAVANAKUMAR S. Fast blur kernel estimation with texture preserving DRD for motion deblur[J]. Procedia Engineering，2012，38：442-447.

[9] MICHAL D， LIBOR M， TOMAS F. Blurred image restoration: A fast method of finding the motion length and angle[J]. Digital Signal Processing，2010，20：1677-1686.

[10] FANY H， WEIX M， QINS Y. Fast and robust deblurring method with multi-frame images based on PSF estimation and total variation optimization[J]. Optik，2013，124：2285-2291.

Fast Restoration Algorithm of Noise-Free Images Based on Cepstrum

WEIXin,CHENGuang-feng

(Engineering Research Center of Advanced Textile Machinery, Ministry of Education, Donghua University, Shanghai 201620, China)

Abstract:For the problem of current motion blurred image restoration focusing on non-real-time research, that is, focusing on the quality of the algorithm rather than considering the executed efficiency of the algorithm, a fast restoration algorithm of noise-free images based on cepstrum is raised. The blur direction and blur length are directly generated from the cepstrum, which is elaborated by the algorithm of noise-free image. For images with large size, a compression of bilinear interpolation is completed initially then goes the cepstrum of the compressed image. The wiener filtering for image restoration is selected under the comparison with various restoration algorithm, regarding the efficiency and effectiveness. Hence through the deblur experiments on blurred images, restoration effect can be demonstrated along with the high performance efficiency.

Key words:motion blur; biliner interpolation; cepstrum; wiener filtering; image restoration

文章編號：1671-0444(2016)02-0228-06

收稿日期：2015-04-01

基金項目：中央高?；究蒲袠I務費專項資金資助項目(2232013D3-44)

作者簡介：魏鑫(1990—)，男，安徽蚌埠人，碩士研究生，研究方向為智能檢測. E-mail: weixin3032503@163.com 陳廣鋒(聯系人)，男，副教授，E-mail: chengf@dhu.edu.cn

中圖分類號：TP 753

文獻標志碼：A