廣義不變凸函數多目標規劃的對偶性
◎雷 鳴 李文鈺 姜元政
(北華大學數學與統計學院,吉林 吉林 132013)
廣義不變凸函數多目標規劃的對偶性
◎雷 鳴 李文鈺 姜元政
(北華大學數學與統計學院,吉林 吉林 132013)
本文討論了不變廣義凸函數多目標規劃的對偶理論,弱對偶,直接對偶和逆對偶定理.將文[1],[2]的結果給予推廣.
不變廣義凸函數;多目標規劃;對偶理論
【項目】吉林省教育廳“十二五”科學技術研究項目:吉教科合字[2015]第133號.
一、引 言
多目標規劃的對偶理論在多目標規劃理論中占有重要的地位,它對多目標最優化問題中的求解以及最優性條件的揭示中都起到重要的作用.因此,好多學者都在不斷地進行深入的研究.
本文討論了如下形式的多目標規劃(VP)和其對偶規劃(VD)的對偶理論.
其中x∈En,f(x),g(x)和h(x)分別為p維、m維和s維的向量函數.?uΤg(x)+vΤh(x)?表示每個分量都是uΤg(y)+vΤh(y)的p維向量函數u∈Ep,v∈Es,λ∈Ep稱(VD)為(VP)的Lagrange對偶問題.
文獻[1]和文獻[2]分別討論了偽凸和擬凸多目標規劃的對偶理論.本文就不變凸函數的一般情況給出了它的對偶理論.從而推廣了文[1],[2]的結果.
二、定義與引理
記P={x|x∈En,g(x)≤0,h(x)=0,x≥0},稱P為多目標規劃(VP)的可行域.
D={w|w=(y,u,v),u≥0,λΤf(y)+uΤg(y)+vΤh(y)=0}為(VD)的可行域.
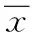
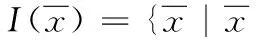
定義2 稱F(x)是集合X?En上的次線性泛函,如果F(x)滿足:
(1)正齊次性:對?α≥0及x∈X,有F(αx)=αF(x)成立;
(2)次可加性:對?x,y∈X,有F(x+y)≤F(x)+F(y)成立.
我們構造如下的單目標規劃:
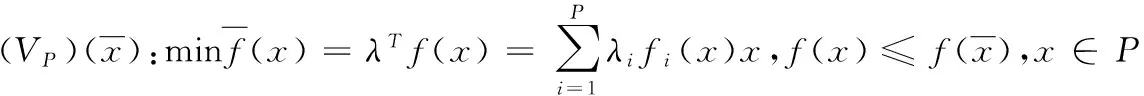
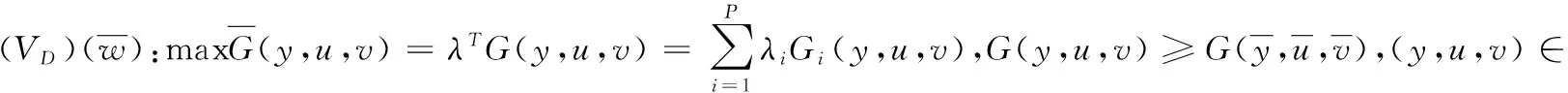
三、(VP)與(VD)的對偶理論
對于廣義F-凸函數而言,原問題(VP)的對偶問題(VD)具有如下形式,仍將其記為(VD).其可行域仍記為D,即
定理1 (弱對偶定理)若存在次線性泛函F(x),使f(x),g(x),±h(x)的每個分量函數都是P上的關于F(x)的F-凸函數.則對任意的x∈P,w=(y,u,v)∈D及λ∈Λ+,都有λTf(x)≥λG(y,u,v)成立.
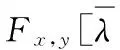


不難證明,在定理1,2,3中將F-凸函數分別換成F-擬凸和F-偽凸函數時,則各定理仍然成立.即(VP)與(VD)之間關于有效解仍是對偶的.在此不予重述.
[1]林銼云.多目標非線性規劃的對偶理論[J].高等學校計算數學學報,1981,3(1):18-26.
[2]林銼云.多目標廣義凸規劃對偶理論[J].江西大學學報,1988,3(3):3-13.
[3]MAHanson.OnSufficiencyoftheKuhn-Tuckercomditious.J.Math.Anal[J].1981,80(2):545-550.

