基于奇異值分解的慣性測量組合減振系統非線性剛度識別
張鵬飛,蘇華昌,吳家駒
?
基于奇異值分解的慣性測量組合減振系統非線性剛度識別
張鵬飛,蘇華昌,吳家駒
(北京強度環境研究所,北京,100076)
介紹了基于奇異值分解的復解析小波脊線提取方法,并用仿真算例進行了驗證。設計了基于沖擊響應的非線性剛度識別程序。采用半正弦沖擊對慣組減振系統的非線性特性進行試驗研究,驗證了方法的可行性,分析了非線性系統剛度和阻尼的變化規律。對于非線性特征比較明顯的結構,使用該方法的參數識別結果具有較高精度。
非線性剛度;小波變換;奇異值分解;小波脊線
0 引 言
結構動力學分析與試驗相關性研究的目的是通過試驗結果修改數學模型,然后用修正后的數學模型計算復雜振動載荷下的響應,這對于線性系統來說困難不大。然而,火箭和航天器實際上呈現出某種程度的非線性品質[1]。非線性可能是由結構(端頭快速連接)、幾何(飛船的支撐機構)和材料性質(阻尼減振器)等因素造成的。雖然業內已有許多非線性系統的結構動力學分析軟件,但是大多數都需要知道特征化的非線性特征。因此,通過試驗識別結構非線性特征是一個亟待解決的問題。
慣性測量組合(慣組)是測量導彈運動姿態的裝置。為了提高慣組在振動環境中的適應性,經常將慣性敏感器件通過橡膠減振器連接到載體上[2]。慣組小系統頻響特性測量結果表明,這個彈性環節呈現出很強的非線性。圖1為實測的慣組角振動傳遞率隨頻率的變化曲線,其傳遞率特征隨激勵量級的變化很大,系統的增益和諧振頻率隨激勵量級下降,這表明系統呈現出含有漸軟剛度的非線性特征。
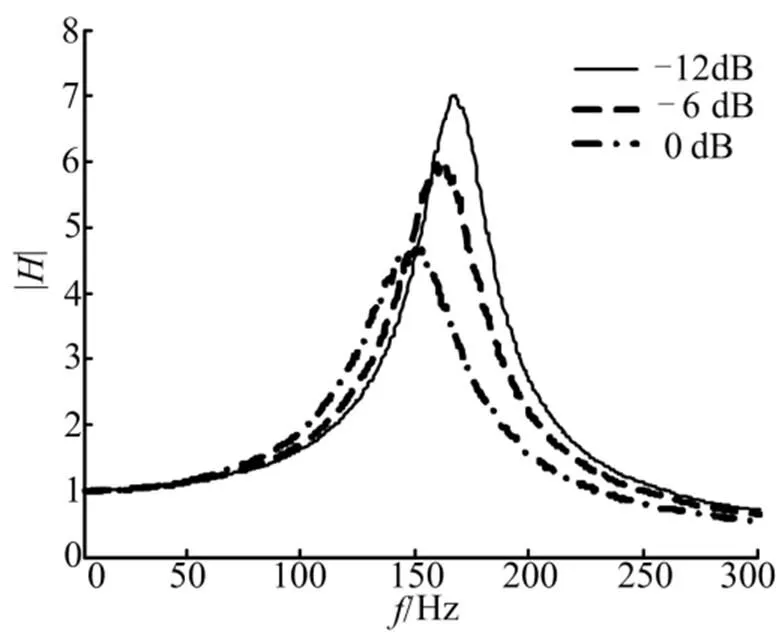
圖1 慣組減振系統角振動傳遞率
目前,對于減振器非線性剛度的識別,多是基于靜剛度或正弦定頻試驗的剛度曲線,使用最小二乘原理進行擬合[3,4]。然而減振器使用環境多數存在沖擊載荷,在更接近真實使用環境下對非線性參數的識別結果更加適用。本文基于非線性減振系統的沖擊響應,給出了基于復解析小波和奇異值分解的非線性剛度識別方法,識別出剛度-載荷曲線,并用含橡膠減振器的慣組試驗數據進行了驗證,結論對于慣組減振器系統非線性參數識別和建模具有一定的參考價值。
1 基于奇異值分解的復解析小波脊線提取法
非線性系統的沖擊響應具有非平穩信號特征。小波脊線能較好地揭示信號瞬時頻率的變化情況。復解析小波變換將小波變換和Hilbert變換緊密結合在一起,具有一定的自適應分析能力。通過復函數連續小波變換得到小波尺度譜后,使用奇異值分解(Singular Value Decomposition,SVD)方法降噪,然后通過求小波系數的模極大值點來提取小波脊線[5~7]。該方法更加適用于試驗獲得的低信噪比信號的小波脊線提取。
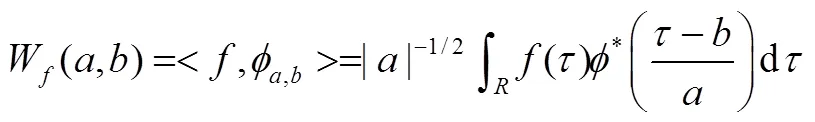
復解析小波函數具有如下的表達形式:
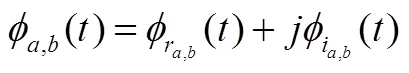
(3)
式中
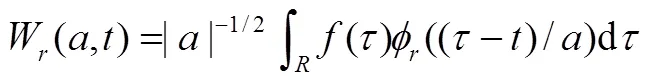
(5)
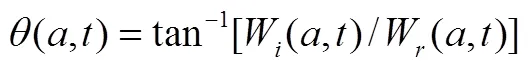
(7)
由小波變換的定義可知,小波變換相當于一系列帶通濾波器對信號進行多帶通濾波,帶通濾波器的中心頻率和帶寬與尺度成反比,且帶寬隨中心頻率的變化自動調節,體現了對信號的自適應分析能力。復解析小波變換實現了信號帶通濾波和Hilbert變換的統一,自適應地提取信號的包絡等特征。
小波尺度譜可定義為

在某一時刻小波系數的最大值滿足
(9)
當取不同的值,所有的最大值點的集合形成了小波脊線。理論上可以通過直接求出時頻面上每一時刻小波系數的模極大值來獲得信號中各分量對應的小波脊線,這是最簡單的一種脊線提取方法,但極易受到噪聲干擾,因此不適合工程應用。
SVD是一種常用的時頻濾波方法,可用于消除信號中的隨機噪聲成份,提取信號中的周期成份[9],本文選取該方法對小波尺度譜進行降噪。設矩陣表示信號的小波尺度譜,在奇異值理論中,秩為的×階矩陣的奇異值分解可表示為
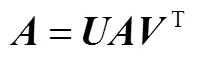
式中和分別是×階和×階正交矩陣,=diag(σ1,σ2,…,σ,0,0,…,0)是×階對角矩陣,其對角元素為的奇異值,并按降序排列。根據Frobeious范數意義下矩陣最佳逼近定理,信號在小波域中有用的信號主要由前個較大的奇異值反映,噪聲信號由后面較小的奇異值反映,去掉代表噪聲信號的較小奇異值,則源信號中的噪聲被去除。為了確定有用的奇異值,首先定義奇異值σ所占能量比重為
(11)
然后,給定一個閾值,將滿足r<(=1,…,)的奇異值置零,再進行奇異值分解的逆運算,最終得到矩陣,那么矩陣就是矩陣的秩為的最佳逼近矩陣,就是降噪后的小波尺度譜。
對小波尺度譜進行SVD濾波后,就可以通過選取各個時刻小波系數模極大值點對應的尺度來提取小波脊線。
2 仿真算例
為了驗證復解析小波及其脊線提取方法在非平穩信號處理中的先進性,取仿真信號進行試驗。仿真信號由下式給出:
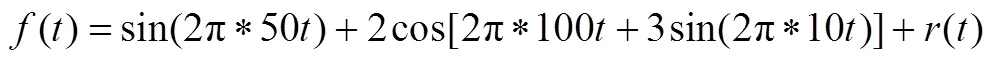
式中()是方差為1的白噪聲,[0,1]。

圖2 信號f(t)的時域波形

a)直接模極大值法
b)基于SVD的復解析小波模極大值法
圖3 不同方法所得()小波脊線的對比
3 非線性剛度識別
3.1 非線性系統的數學模型
根據圖1中所表現出來的慣組減振器系統的非線性特征,本文對減振器采用立方剛度模型表征。這種情況下,力-位移關系具有以下形式[10]:
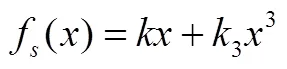
(14)
式中為質量;為阻尼系數。
3.2 非線性剛度識別程序設計
對于式(14),采用諧波平衡法求解,可以得到頻率和振動幅值間存在如下的關系:
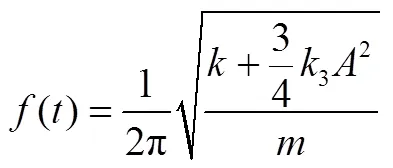
根據式(15),當已知質量時,根據自由衰減信號的小波脊線提取的頻率和幅值信息,采用最小二乘原理可以識別出和。對于粘性阻尼,自由衰減信號存在指數形式的包絡曲線:
(16)
非線性剛度的識別程序可以匯總為:
a)用敲擊法或基礎激勵法測得系統的加速度自由衰減時間歷程;
b)用數字積分獲得位移自由衰減時間歷程;
c)連續復解析小波變換;
d)SVD濾波降噪;
e)取小波系數模極大值得到脊線;
f)從脊線計算瞬時頻率的包絡;
g)由衰減包絡擬合得到的曲線識別出非線性參數值。
4 實際信號分析
用包含橡膠減振器的慣組來檢驗上述方法。慣組通過橡膠減振器連接在振動平面上,電動振動臺對振動平臺施加半正弦沖擊激勵。振動控制點在振動平面上,慣組上安裝加速度傳感器測量減振后信號,試驗原理如圖4所示。圖5為實測的慣組減振后加速度自由衰減時間歷程。
在Matlab軟件中使用數字積分法對加速度信號進行積分,獲得位移的自由衰減時間歷程。初始速度和初始位移的影響可通過離散小波變換消除積分結果中的直流分量和趨勢項來消除。對位移信號進行連續小波變換得到小波尺度譜,并選取每個時刻下小波系數模的最大值,得到如圖6所示的小波尺度譜的等高線和脊線。
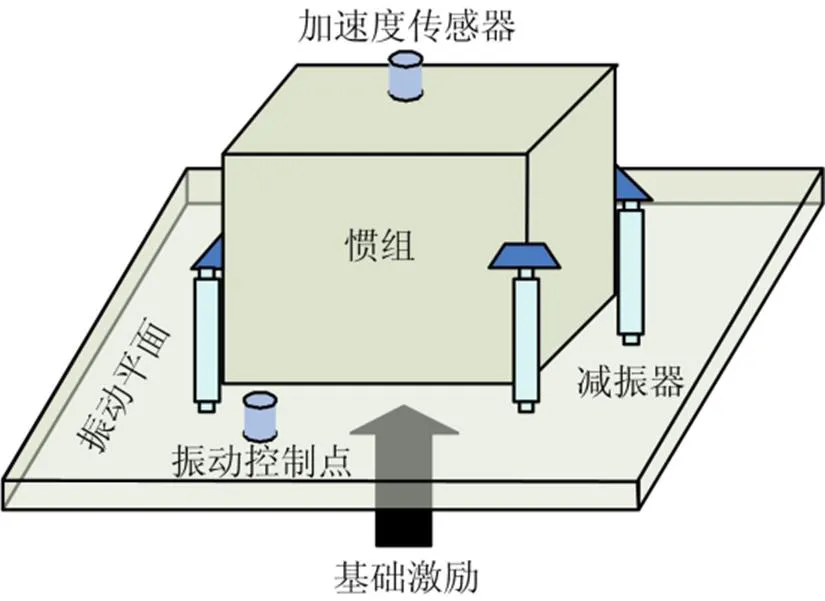
圖4 慣組基礎激勵試驗原理
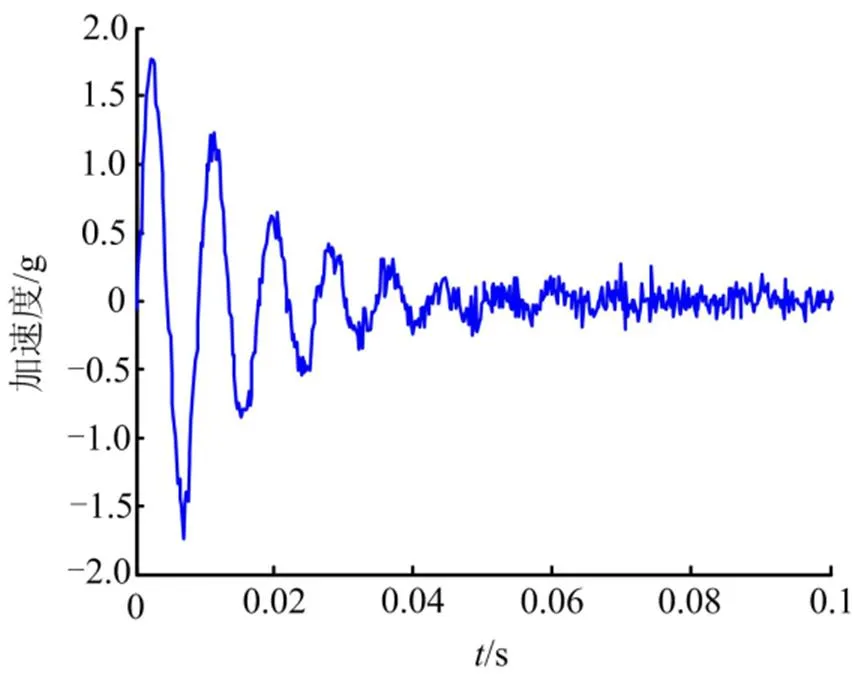
圖5 自由衰減時間歷程
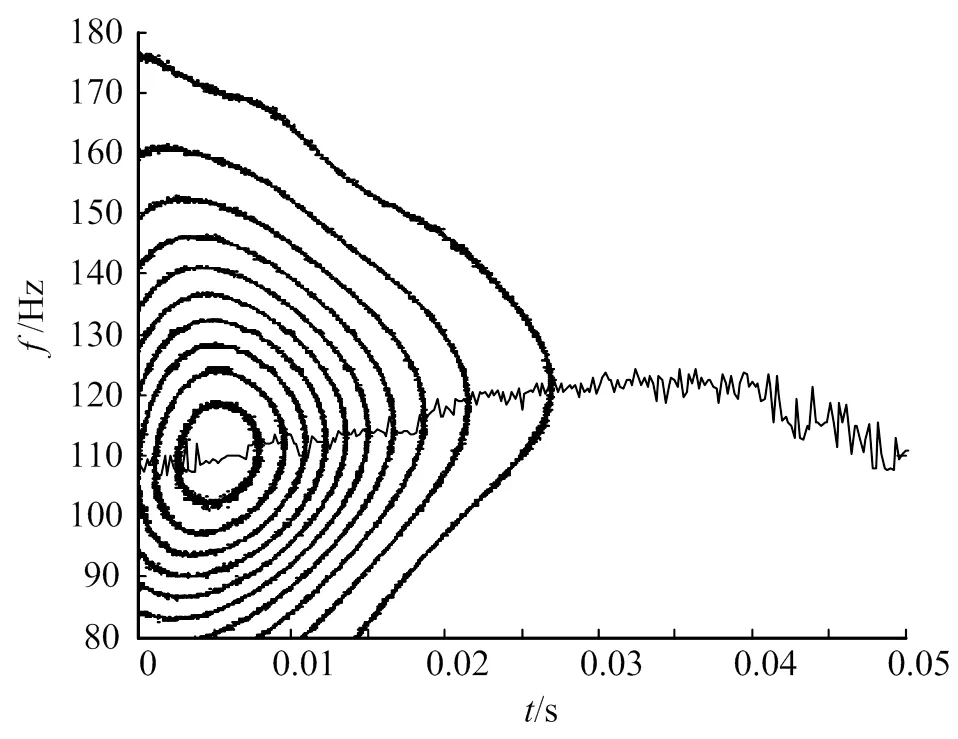
圖6 小波尺度譜的等高線和脊線
由于信號噪聲較大,提取到的脊線不光滑。通過SVD法對時頻譜進行降噪,閾值取0.02,降噪后的小波尺度譜等高線和脊線如圖7所示。SVD降噪后脊線光滑,準確反映了瞬時頻率隨時間的變化。

圖7 SVD降噪后的小波尺度譜等高線和脊線
對位移自由衰減信號進行Hilbert變換后獲得其幅值包絡曲線,結合小波脊線得到瞬時頻率隨振動幅值變化的曲線,如圖8所示。取固定時間間隔為0.1 s,隨著的平移,計算出結構粘性阻尼隨時間的變化函數,進而得到阻尼比關于振動幅值的函數,如圖9所示。
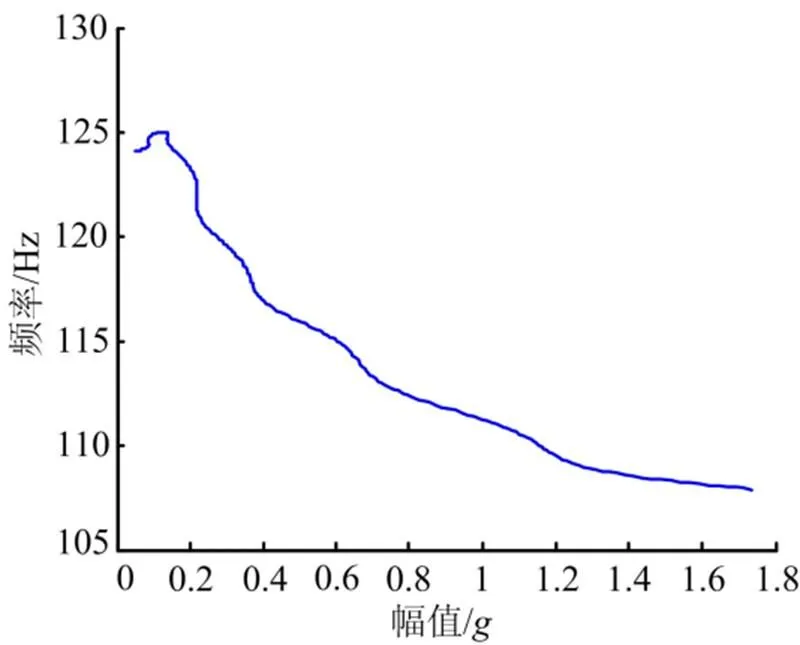
圖8 瞬時頻率隨振動幅值的變化
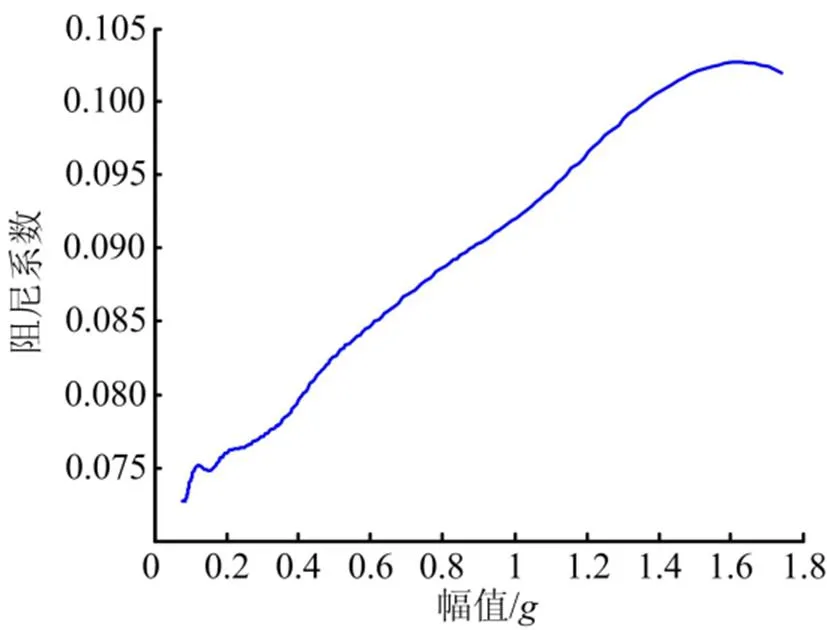
圖9 阻尼系數隨振動幅值的變化
根據式(15),進一步得到如下關系:
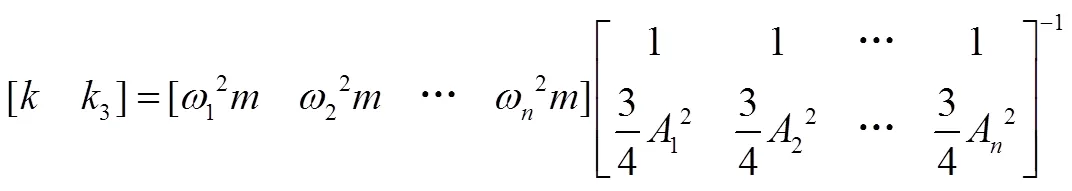
式中為采樣點數。
將圖8中的頻率和幅值代入式(17),得到最小二乘意義下的剛度和。從該組試驗數據識別出慣組減振系統的線性剛度=5.66×106N/m,立方剛度=-1.68×1013N/m3。
試驗的識別結果表明橡膠減振器符合漸軟系統的非線性特征:隨加載量級加大剛度變小,阻尼增大。根據沖擊響應識別出的非線性剛度特征與文獻[3]中使用定頻激勵法的結果規律一致。根據識別出的頻率和阻尼特性,可以擬合出結構的非線性頻響函數隨不同加載量級的分布,如圖10所示。從圖10可以看出,隨著加載量級的增加,結構的共振頻率降低,共振幅值降低,這與圖1中的試驗結果規律一致。為了驗證參數識別的精度,將上述識別出的非線性剛度參數代入式(14)中,使用4階Runge-Kutta法得到相同激勵下的響應曲線,并與實測曲線進行對比,如圖11所示。從圖11中可見,實測曲線與計算曲線符合很好,說明識別出的和具有較高精度。

圖10 擬合后的非線性頻響函數

圖11 實測與計算結果對比
5 結 論
本文在電動振動臺上模擬沖擊使用環境,對慣組減振系統的非線性特性進行研究,主要得到以下結論:
a)利用基于SVD的復解析小波脊線提取方法,準確地得到減振后自由衰減信號的時頻分布。試驗表明SVD法能有效降低噪聲的影響,有利于準確提取小波脊線,進而得到慣組減振系統的頻率-幅值曲線。
b)根據慣組減振系統的傳遞特性試驗數據所表現的特點,建立了軟特性三次剛度動力學模型。考慮到減振器的使用環境多數存在沖擊載荷,設計了基于沖擊響應的非線性剛度識別程序。
c)使用慣組減振系統半正弦沖擊試驗的自由衰減數據進行非線性參數識別,驗證了模型和識別方法的有效性。分別在頻域和時域對參數識別結果與試驗進行對比,表明非線性剛度識別具有較高的精度。研究結果對于慣組減振器系統非線性參數識別和建模具有一定的參考價值。
[1] 李欣業, 陳予恕, 張琪昌. 火箭非線性動力學行為研究中的若干問題[J]. 河北工業大學學報, 2001, 30(6): 74-78.
[2] 姚建軍. 捷聯慣導系統不同隔振模式的比較[J]. 強度與環境, 2009, 36(2): 19-27.
[3] 樊文欣, 楊桂通, 趙俊生, 李雙虎. 金屬橡膠減振器非線性建模及仿真研究[J]. 車用發動機, 2009(5): 53-56.
[4] 韓德寶, 宋希庚, 薛冬新. 橡膠減振器非線性動態特性的試驗研究[J]. 振動工程學報, 2008, 12(1): 102-106.
[5] Staszewski W J. Identification of non-linear systems using multi-scale ridges and skeletons of the wavelet transform[J]. Journal of Sound and Vibration, 1998, 214(4): 639-658.
[6] 吳宏鋼, 秦毅, 秦樹人. 基于重分配配算法和奇異值分解的多小波脊線提取[J]. 振動與沖擊, 2009, 28(12): 9-14.
[7] Brenner M. Nonstationary dynamics data analysis with wavelet-SVD filtering[R]. AIAA-2001-1586, 2001.
[8] 張家凡, 易啟偉, 李季. 復解析小波變換與振動信號包絡調解分析[J]. 振動與沖擊, 2010, 29(9): 93-96.
[9] 錢征文, 程禮, 李應紅. 利用奇異值分解的信號降噪方法[J]. 振動、診斷與測試, 2011, 31(4): 459-463.
[10] 陳前, 高雪. 結構動力學中的非線性問題[M]. 北京: 機械工業出版社, 2012.
Identification of Nonlinear Stiffness of Inertial Measurement Unit with Vibration Absorber System Based on Singular Value Decomposition
Zhang Peng-fei, Su Hua-chang, Wu Jia-ju
(Beijing Institute of Structure and Environmen Engineering, Beijing, 100076)
Wavelet ridge extracting method based on singular value decomposition(SVD) was introduced. A numerical example was actualized to validate the method. Programs of identifying nonlinear stiffness based on impulse response were designed. The experiment of inertial measurement unit with rubber vibration absorber under the load of half sine pulse was conducted to validate the feasibility of the method. The changing regularities of nonlinear stiffness and damp were analysed. Using this method, the parameter identified results are high precise to nonlinear system.
Nonlinear stiffness; Wavelet transformation; Singular value decomposition; Wavelet ridge curve
1004-7182(2016)03-0068-05
10.7654/j.issn.1004-7182.20160316
V214
A
2015-06-10;
2015-08-03
張鵬飛(1986-),男,工程師,主要研究方向為結構動力學

