“線性代數”教學實踐改革探討

代愛鳳 李瑜鳳

[摘 要] “學習的最終目的不只是為了學到課本上的知識，還要注重學生能力的發展”這一新課程理念促使了教學模式和方法的多樣化。以線性代數課程教學過程為例，有針對性地探討了合作學習的教學模式以及案例教學法在教學實踐改革中的具體實施過程，以供同行參考。

[關 鍵 詞] 線性代數；合作學習；案例教學法；教學改革

[中圖分類號] G642 [文獻標志碼] A [文章編號] 2096-0603（2016）28-0190-01

線性代數是 高等院校有關專業的一門基礎課，是學習專業知識必需的基礎知識和重要工具。但就線性代數課程本身而言，它需要嚴謹的邏輯思維以及繁瑣的計算過程，這使得很多學生對這門課程失去了學習的信心和興趣，從而大大降低了大學生學習數學的主動性和積極性。為了讓學生更好地掌握理論知識和更好地培養大學生的綜合素質，教師需要針對線性代數這門課程的相關知識點，并結合學生的學習現狀，改變傳統的教學（思維）模式和教學方法。

一、教學模式的改革

要建立以培養學生對知識的分析和創新應用能力為目標的“合作學習”教學模式。該教學模式主要是以小組討論的形式體現。教師需要把班級中的學生按照他們的綜合能力水平平均分配到每個小組中，以小組為單位進行討論和學習，采用提問—討論—回答的討論式模式進行學習。這給學生提供了一個自學、自說、自練的平臺，在學習理論知識和應用知識的同時，對學生的綜合素質也進行了培養。

二、教學方法的改革

需要改變傳統的“以教師為中心的教和以測驗為目的的學”的教師單一授課方式，通過案例引入，以提高學生對線性代數這門課程學習的興趣和積極性，通過小組討論，查閱相關資料，解決問題，進而達到掌握理論知識的目的。

（一）興趣案例式教學

興趣案例教學法是為了提高學生學習的興趣，引入一個案例，然后分析案例，再進行相互討論，從中運用我們所學的知識和技能，以及將要學習的知識來解決這類問題，進而掌握理論知識的一種教學方法。例如，在講完矩陣的概念以后引入一個案例，來提高學生學習的興趣，小組討論后得出結論。

案例：齊國大將田忌與齊王進行賽馬比賽，約定各出上、中、下三個等級的馬匹進行比賽，比賽共3場，勝者得1分，勝負者得-1分。同等級的馬進行比賽，齊王贏。若齊王的中等馬對田忌的上等馬，或齊王的下等馬對田忌的中等馬，則田忌贏，齊王和田忌賽馬的出場順序如下：

上、中、下上、下、中中、上、下中、下、上下、中、上下、上、中將這6種策略依次編號，寫出齊王獲勝的矩陣。

（二）與數學建模相結合的應用性案例式教學

理論知識是分析解決實際問題的工具，因此，在授課過程中還要注重對學生綜合解決問題能力的培養。下面以交通問題為案例，具體講解一下教學的過程。

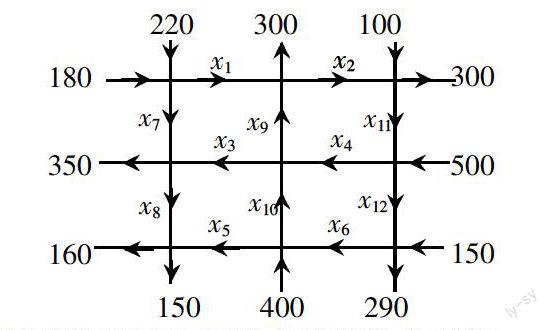
1.模型準備（提出問題）：下圖為某城市的交通圖，現已經調查到每條道路每小時的車流量.圖中的數字表示該條路段的車流數.

（1）建立以道路流量為均衡點的線性方程組。

（2）分析哪些流量數據是多余的。

2.模型假設：每個交叉路口進入和離開車數相等，而且均為單行車道。

3.模型建立：根據圖示和上述假設，列出線性方程組。

4.模型求解：求解上述線性方程組，在求解的過程中利用行列式或矩陣的相關知識。

5.模型分析：根據（A，b）的行最簡形進行問題分析。

（三）問題式教學

美國教育家魯巴克認為：“最精湛的教學藝術遵循的最高準則，是學生自己提出問題。”因此，在讓學生掌握理論知識的過程中，還要培養學生提出、分析、解決問題的能力。

具體實施過程：教師提前把任務書或學案發給學生，上課時，由學生自己提出問題，即可以是在預習過程中遇到的任何疑問，然后各個小組針對這些問題進行具體討論，各個小組進行答疑，最后教師再根據討論結果進行進一步的補充和總結。在提問、討論、答疑的過程中，不僅提升了他們學習的積極性和主觀能動性，而且在掌握理論知識的同時，也提高了他們的團隊合作能力和分析解決問題的能力。

結合當前的經濟建設和社會發展對高素質應用型人才培養的需求，通過合作學習式課程改革不僅可以讓學生學好扎實的數學理論知識，還培養了他們的自學能力、團隊協作能力及分析解決問題的能力，使他們更具有競爭力。

參考文獻：

[1]劉春林，李寶娣.線性代數與案例教學的體會與思考[J].湖南理工學院學報（自然科學版），2016（2）.

[2]王劍.問題驅動教學在線性代數教學中的應用[J].天津職業技術師范大學學報，2016（6）.

[3]趙曉.應用型本科院校線性代數教學的若干建議[J].東莞理工學院學報，2016（5）.

[4]戴立輝，陳翔.考研線性代數重點內容及常見題型[J].教育教學論壇，2016（47）.

[5]薛慶平.論如何將實例結合在線性代數教學中[J].赤峰學院學報（自然科學版），2016（17）.

[6]盛瑩，王洪曾.淺談線性代數課程改革與創新[J].數學學習與研究，2016（15）.

[7]蔡海鷗.《線性代數》教學方法探索[J].首都師范大學學報（自然科學版），2009（5）.

[8]李尚志.從問題出發引入線性代數概念[J].高等數學研究，2006（5）.