淺談微分與積分之間的關系
摘 要: 本文主要以均勻和非均勻物質分布為基礎,采用了局部均勻求近似,利用極限得精確的數學思想方法,探討了導數和積分是處理均勻量中的乘法和除法在處理相應的非均勻事物的發展,簡單地分析積分和微分之間的關系。
關鍵詞: 微積分 均勻 非趙紅妮均勻
由于物體運動過程中某一時刻的瞬時速度、曲線在一點處的切線問題、函數的最值、曲線長、曲線圍成的面積、曲面圍成的體積、物體的重心等這一系列問題的出現促使了微積分的誕生。國際數學家教育委員會前主席、荷蘭數學家H.Freudental說:“沒有一種數學思想以它被發現時的那個樣子發表出來,一個問題被解決以后,相應地發展成為一種形式化的技巧,結果使得火熱的思考變成冰冷的美麗。”
任何事物都有其微觀和宏觀不同的表現形式,現將其簡單地歸納如下。
通過上表可以看出,任何事物都有兩面性的體現,而我們所探討的微分與積分也是在初級教學中乘法除法的一個延伸,用以解決實際中的問題。
1.均勻與非均勻物質變化率
現以均勻與非分布的物質從質量分布的細密程度、單位長度上的變化、變化率、函數表達式及圖形來對比兩者之間的共性和不同。
通過表2可以看出,非均勻分布與均勻分布基本類似,非均勻物質在各方面的表示都是均勻物質的推廣,由線性函數到非線性函數,從直線到曲線,均勻物質是非均勻物質分布的特殊情況,而非均勻物質是均勻物質的推廣。
2.微積分方法的本質(物質細棒)
不管從微觀還是宏觀角度而言,解決的基本思想方法是一樣的“局部均勻求近似”“利用極限得精確”;導數與定積分分別是處理均勻量的商和積在處理相應的非均勻量中的發展;均勻物體用乘除法,非均勻物體采用微積分。
3.微分與積分的關系
現以線密度為μ(x),求質量為m(x),探討微分與積分的關系。
1)在微小一段[x,x+Δx]上對μ(x)以“不變代變”,求質量m(x)增量的近似值。
對上式兩邊求微分可得=μ(x),則m(x)為μ(x)的原函數,而μ(x)是m(x)的導函數,兩者之間是原函數與導函數的關系。
2)同理是否可在[a,b]區間上對導函數μ(x)以“不變代變”求原函數m(x)增量的近似值呢?上述這個例子是否具有普遍性?
假設F= f(x)dx成立,則可推出F(x)= f(u)du,u∈(a,b)。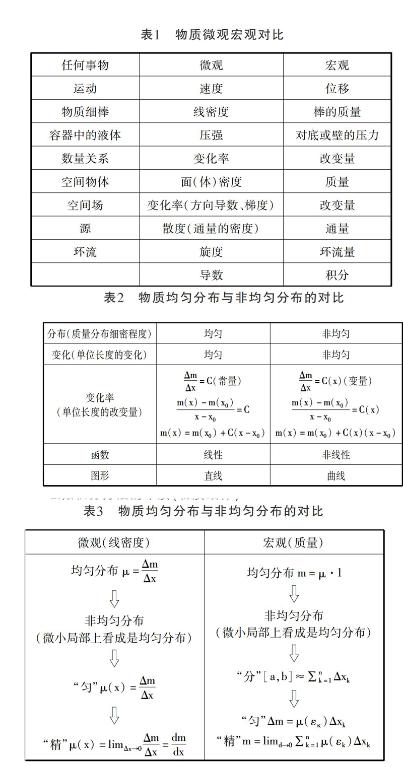
若f(x)是[a,b]上的連續函數,則有
假設f(x)是[a,b]上的連續函數,則有
通過上式可以看出
4.總結
1)導數和積分是商和積的發展,即導數和積分是處理均勻量中商和積兩個概念在處理相應地非均勻量事物的發展,也就是說導數和積分是處理均勻量中的乘法和除法在處理相應的非均勻量事物的發展;
2)積分是微分的無限累加,求積分的關鍵在于求微分;
3)求微分就是尋找所求量的微小增量的線性主部,通常可先尋找所求量非均勻分布的某一量,由于此量的變化造成非均勻分布,將此量在微小局部以“不變代變”便可得到所求微分。

