水平與豎向加速度-時程曲線疊加效應下邊坡永久位移計算的極限上限分析

王志斌，湯祖平,趙煉恒，程肖

(1. 湖南科技大學 土木工程學院，湖南 湘潭 411201；2. 上海市政工程設計研究院有限公司深圳分院，廣東 深圳 518013; 3. 中南大學 土木工程學院，長沙 410075)

?

水平與豎向加速度-時程曲線疊加效應下邊坡永久位移計算的極限上限分析

王志斌1，湯祖平2,趙煉恒3，程肖3

(1. 湖南科技大學 土木工程學院，湖南 湘潭 411201；2. 上海市政工程設計研究院有限公司深圳分院，廣東 深圳 518013; 3. 中南大學 土木工程學院，長沙 410075)

摘要：實際邊坡動力穩定性受地震豎向與水平方向效應共同作用，傳統邊坡地震永久位移計算方法較少考慮豎向地震波影響，采用實際地震的豎向與水平方向加速度-時程曲線共同效應更符合工程實際。基于極限分析上限法和Newmark剛塑性滑塊模型，提出一種基于實際水平向與豎向地震加速度-時程曲線的邊坡永久位移計算改進方法，以3個工程邊坡為例，探討了兩組具有代表性實測典型水平和豎向地震地面運動記錄對邊坡地震永久位移計算的影響。研究結果表明：不考慮豎向地震加速度-時程曲線時，本文方法可蛻化為與前人方法兼容；不同地震波的豎向與水平地震動時程曲線的疊加效應不同，豎向地震對邊坡永久位移的影響不可忽略。

關鍵詞：邊坡；地震永久位移；加速度-時程曲線；Newmark法；極限分析上限法

1965年，Newmark[1]提出了估算地震滑移量的剛塑性滑塊模型，并給出了采用邊坡滑移量代替安全系數以評價邊坡的抗震性能的建議。過去50年中，基于Newmark“滑塊模型”，許多學者結合土工試驗與實際震害資料，進一步探討了地震作用下邊坡的永久位移問題[2]。Chang等[3]將Newmark的剛塑性滑塊模型應用在自然邊坡的地震穩定性分析中，基于極限分析上限法推導了直線型滑面和對數螺旋滑面邊坡永久位移的計算公式；You 等[4-5]采用極限分析上限法，結合Newmark“滑塊模型”的概念，給出了水平地震效應下邊坡與加筋邊坡永久位移的設計圖表。現有大部分研究均只考慮了水平向地震效應[6-8]，但大量地震譜記錄都表明震中部位的豎向加速度峰值往往也較大[9-13]，關于豎向地震效應對邊坡抗震性能影響的研究日益受到學者們的重視和關注[14]。欒茂田等[15]基于兩種曲面滑動面(圓弧和光滑漸變非圓弧)，并考慮水平向與豎向加速度響應，對于滑體位移計算模型進行了改進。分析表明：潛在滑動體的地震位移總是小于僅考慮水平向地震響應加速度時所得到的位移，且滑體位移取決于滑體上水平向與豎向地震響應加速度的綜合作用。Ling等[16]采用極限平衡法和Newmark滑塊模型對陡坡的安全系數與永久位移進行了研究，研究表明：豎向地震效應對陡坡穩定性影響顯著。當水平加速度較大時，豎向加速度對邊坡抗震性能和永久位移的影響不容忽略。Simonelli等[17]應用數值分析方法，針對干砂所組成的無限土坡，選取具有不同頻譜特性的多個實測地震加速度時程曲線，考慮水平與豎向地震加速度的不同組合方式對邊坡永久位移進行分析，分析結果表明：當邊坡永久位移高于厘米級時，豎向加速度影響可以忽略。黃建梁等[18]將豎向加速度幅值固定為水平向加速度幅值的2/3，假定3種水平與豎向地震疊加情況對算例邊坡進行計算，計算表明可以忽略豎向地震加速度的影響。同樣，針對無限邊坡，Jacques等[19]給出了考慮豎向與水平向地震效應下永久位移的計算方法，但研究結果表明：豎向地震效應顯著影響邊坡永久位移。上述研究成果表明，同時考慮水平向和豎向加速度效應對邊坡永久位移的影響時，以往不考慮豎向加速度效應的方法可能低估了同時疊加豎向與水平向地震動效應的影響[20-21]。

此外，傳統方法往往為簡化分析過程，假定豎向與水平地震波波形一致，并假定豎向地震波為水平地震波量值的固定比值。然而，實際地震中豎向地震波與水平方向的地震波的時程曲線并非一致，波形一致假定和量值比例假定可能導致較大誤差。

本文基于極限分析上限法和強度折減技術，提出了一種基于實際水平與豎向方向的地震加速度-時程曲線的邊坡地震永久位移計算方法。采用極限分析上限法，結合Newmark“滑塊模型”的概念，按照地震波水平與豎向加速度-時程曲線特性，提出一種基于水平加速度-時程和豎向加速度-時程曲線的邊坡永久位移計算方法，探討兩組具有代表性實測典型水平和豎向地震地面運動記錄對邊坡永久位移的影響。

1基于水平加速度-時程曲線的邊坡永久位移簡化計算方法

基于極限分析上限分析方法，采用對數螺旋面旋轉破壞機構開展地震作用下邊坡永久位移分析。破壞機構引用Chen[22]、Chang等[3]和You等[4]提出的經典機構，并考慮了豎向地震影響效應[23]，如圖1所示。

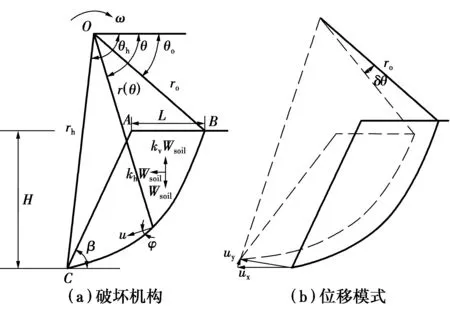
圖1　邊坡旋轉破壞機構[3-4] ,[22-23] Fig.1　Rotational failure mechanism for slope

圖1中：H為邊坡豎直高度，m；β為邊坡傾角，(°)；kv表示豎向地震加速度系數；kh表示水平地震加速度系數，且kv=αv/g，kh=αh/g，αv、αh分別為豎向和水平地震加速度；g為重力加速度；θ0和θh為角度參數，用于描述對數螺旋線破壞機構形態；r為與θ定義相對應的極徑；r0為θ=θ0相對應的極徑；φ為巖土材料內摩擦角。同時，本文應用了如下假定：1)分析問題基于平面應變條件考慮；2)巖土體材料假定為理想剛塑性體，服從摩爾庫倫強度準則，并遵循相關聯流動法則；3)邊坡內部孔隙水壓力效應、巖土體抗剪強度參數c和φ因地震影響而發生弱化均不考慮；4)引入水平和豎向效應時采用常見的擬靜力方法。

水平和豎向地震作用下邊坡處于臨界極限狀態時，外力功率包括滑體自重和地震力所做功率，內部耗能沿滑面發生[23]。邊坡滑體自重功率、豎向和水平地震效應所做功率和間斷面BC發生的內部耗能計算過程參見文獻[3，4，22] 。

為進行對比計算并簡化分析過程，類似傳統Newmark“滑塊模型”分析方法，首先假定豎向地震波與水平地震波波形一致，并假定豎向地震效應為水平地震效應量值的固定比例值，即kv=λkh成立(λ為kv相對于kh的比例系數)。地震效應下，邊坡處于臨界狀態時，水平地震加速度系數kh恰好達到臨界屈服加速度kc，由功率平衡方程可得

(1)

進而獲得邊坡的屈服加速度kc

(2)

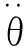
(3)

由式(2)和(3)可得

(4)

式(1)～(4)中：θ0和θh分別為基準線OB和OC與水平線的夾角；γ為材料容重，kN/m3；ω為剛性滑體ABC的角速度；f1～f3，f4～f6為無量綱表達式；l為滑動體重心到轉動圓心O點的距離；G為滑體的重力大小。具體表達式見文獻[3-4]，[18]。

由式(4)可以看出，坡體的轉動加速度是一個與作用在坡體上的地震水平加速度有關的函數。在確定出坡體地震屈服加速度后，對式(4)進行二次積分，便可得到滑塊ABC的累計轉動滑移量，因此，通過幾何關系可求得邊坡坡腳的水平永久位移

(5)

式中：C為位移系數。

(6)

以上分析過程即為假定豎向與水平地震波時程波形一致，并假定豎向地震波時程幅值為水平地震波時程幅值的固定比值，以基于水平加速度-時程曲線的邊坡永久位移簡化計算方法。實際地震中豎向地震波與水平向地震波的時程曲線并非一致，波形一致假定和量值比例假定可能導致計算結果出現較大誤差。以下進一步提出基于水平與豎向加速度-時程曲線的邊坡永久位移計算思路與方法。

2基于水平與豎向加速度-時程曲線的邊坡永久位移計算方法

2.1基本步驟

采用極限分析上限法，結合Newmark“滑塊模型”的概念，以往僅基于水平加速度-時程曲線的邊坡永久位移計算方法直接以水平屈服加速度評估邊坡處于臨界極限平衡狀態，進而估算邊坡地震永久位移量，基本步驟可以概括為：

1)確定臨界屈服加速度，其中臨界屈服加速度為使邊坡處于臨界極限平衡狀態需施加的水平向地震加速度；

2)對于給定水平加速度時程曲線中大于水平屈服加速度的部分進行二次積分便求得滑塊的總位移。

本文由于同時引入了水平和豎向地震影響效應，直接以水平和豎向屈服加速度評估邊坡處于臨界極限平衡狀態時存在困難。故本文通過引入工程實際中常用的以安全系數Fs=1.0為標準來評判邊坡是否處于臨界極限平衡狀態，由此確定邊坡安全系數Fs=1.0為節點對應的水平和豎向臨界屈服加速度，進一步對給定的水平和豎向加速度時程曲線中大于水平和豎向臨界屈服加速度的部分進行二次積分求得對數螺旋線滑塊的總位移。

該分析思路實際上依然是基于Newmark“滑塊模型”假定進行的，區別在于：以往以水平臨界屈服加速度評估邊坡第一次處于臨界極限平衡狀態，本文以水平和豎向地震時程波效應下，邊坡第一次安全系數Fs恰好等于1.0為標準來評判邊坡達到了臨界極限平衡狀態。基于水平與豎向地震加速度-時程曲線計算邊坡永久位移的基本步驟可以概括為：

1)基于實際水平與豎向地震加速度-時程曲線，將水平和豎向地震動時程曲線在有效影響時長范圍內劃分為時間步非常短的多個時間節點；結合強度折減技術，通過從第一個時間節點開始向后遍歷水平和豎向加速度-時程曲線每個時刻，對邊坡進行穩定性分析，結合數學插值方法找出邊坡安全系數Fs第一次等于1.0的時刻(為保證計算精度，設置相對誤差限值為10-3)，此時刻即邊坡開始滑動的時刻；由此獲得相應此刻的水平地震加速度值kh和豎向地震加速度值kv，進一步獲得此時刻邊坡的滑裂面參數(θ0，θh) ，并假定此后邊坡在地震作用下以此滑裂面保持不變。

2)依據所確定第一次滑動的滑動面參數(θ0，θh)，可以通過動力平衡方程求得開始滑動以后邊坡每一時刻的加速度，通過兩次積分便可以求出邊坡在這段時間內所產生的位移，將其累積疊加在一起即為邊坡在整個地震過程中的永久位移。

2.2計算方法和原理

2.2.1強度折減法基本原理采用強度折減法求解邊坡安全系數的物理意義為：對潛在滑動土體的抗剪強度參數折減Fs倍，邊坡恰好過度到臨界平衡狀態[24]。經折減后的巖土材料抗剪強度參數(cf，φf)變為：

(7)

式中：Fs為強度折減系數；c和φ為初始抗剪強度參數，cf和φf為折減后的抗剪強度參數。

2.2.2穩定性分析當邊坡同時受豎向和水平地震影響效應時，滑體外功率和內耗能所滿足的動力平衡方程為

(8)

結合強度折減原理，為確定豎向和水平地震影響效應下邊坡的安全儲備，將原始抗剪強度指標c和φ按式(7)折減并代入式(8)，有

(9)

式中：φf=arctan(tanφ/Fs)，且系數f1～f3，f4～f6中內摩擦角φ均由φf=arctan(tanφ/Fs)替代。

根據極限分析上限定理，式(9)給出了豎向和水平地震影響效應下邊坡安全系數FS的一個上限意義的隱式解答式。當θh、θ0滿足條件

(10)

(11)

時，函數Fs(θh,θ0)取得一個極值，進而得到邊坡安全系數FS的一個基于上限定理意義的解答。

根據上限解答的基本意義，當邊坡體外力做功和內部耗能值為最小時與其對應的安全系數才為邊坡的最小安全系數。即強度折減系數Fs的上限意義解答實際上轉化成了一個最優化問題。對于兩個或兩個以上不同的自變量或自變量組合能得到多個該不同條件下的邊坡臨界狀態。將求Fs最小值問題轉化為約束非線性最優化問題，同時，由于安全系數FS實際上是一個隱函數，因而在進行優化計算時還需要進行迭代運算。通過引入MATLAB中求解單目標多變量非線性約束函數Fmincon函數[25]，編程采用序列二次規劃法進行優化迭代計算，詳細過程可參見文獻[26-27] 。

以上分析過程通過引入工程技術人員熟悉的強度折減技術進行邊坡臨界失穩狀態描述。遍歷地震動時程曲線范圍，尋找到某一時刻的水平和豎向地震影響效應作用時邊坡安全系數Fs第一次恰好等于1.0判定為邊坡第一次達到臨界極限平衡狀態，該臨界狀態即為邊坡開始滑動的時刻，與該臨界狀態對應的水平和豎向加速度即為臨界屈服水平和豎向加速度。

2.2.3地震作用下邊坡開始滑動時刻及臨界滑動面的確定同時考慮水平和豎向地震加速度-時程曲線時，由于并未假定λ=kv/kh為常量，則kv、kh兩者的比例關系不確定，故不能基于傳統Newmark滑塊法如式(9)采用屈服加速度的概念來判斷邊坡的產生滑動的時刻。自1955年Bishop提出強度折減法以來，許多學者都采用此概念來評價邊坡的穩定性，即分析邊坡的臨界狀態。對一個特定邊坡(給定邊坡參數β、γ、c、φ)，以下采用強度折減的概念來判斷邊坡在水平和豎向地震時程效應下邊坡開始產生滑動的初始臨界狀態。具體描述為：

將水平和豎向地震動時程曲線有效影響時長劃分為時間步dt非常短的由(n)個時間節點(t(1)、t(2)、……、t(n-1)、t(n))組成的(n-1)個時段，通過從第一個時間節點t(1)開始向后遍歷水平和豎向加速度-時程曲線第i時刻(kv(i)、kh(i))所對應的Fs(i)，首先找到第一個kv(j)、kh(j)使邊坡失穩的時間點，此瞬時時刻即Fs(j)≤1.0。同樣優化求解并記錄上一瞬時時刻(j-1)邊坡的安全系數Fs(j-1)(Fs(j-1)>1.0)。假定邊坡安全系數在兩個瞬時時刻t(j-1)與t(j)之間線性變化，通過簡單的線性插值法求出邊坡開始滑動(Fs=1.0)的時刻(t(j-1)+Δ)，如圖2所示，其中Δ由三角形的相似原理求得。

(12)

式中：dt為加速度-時程的時間步長取值。

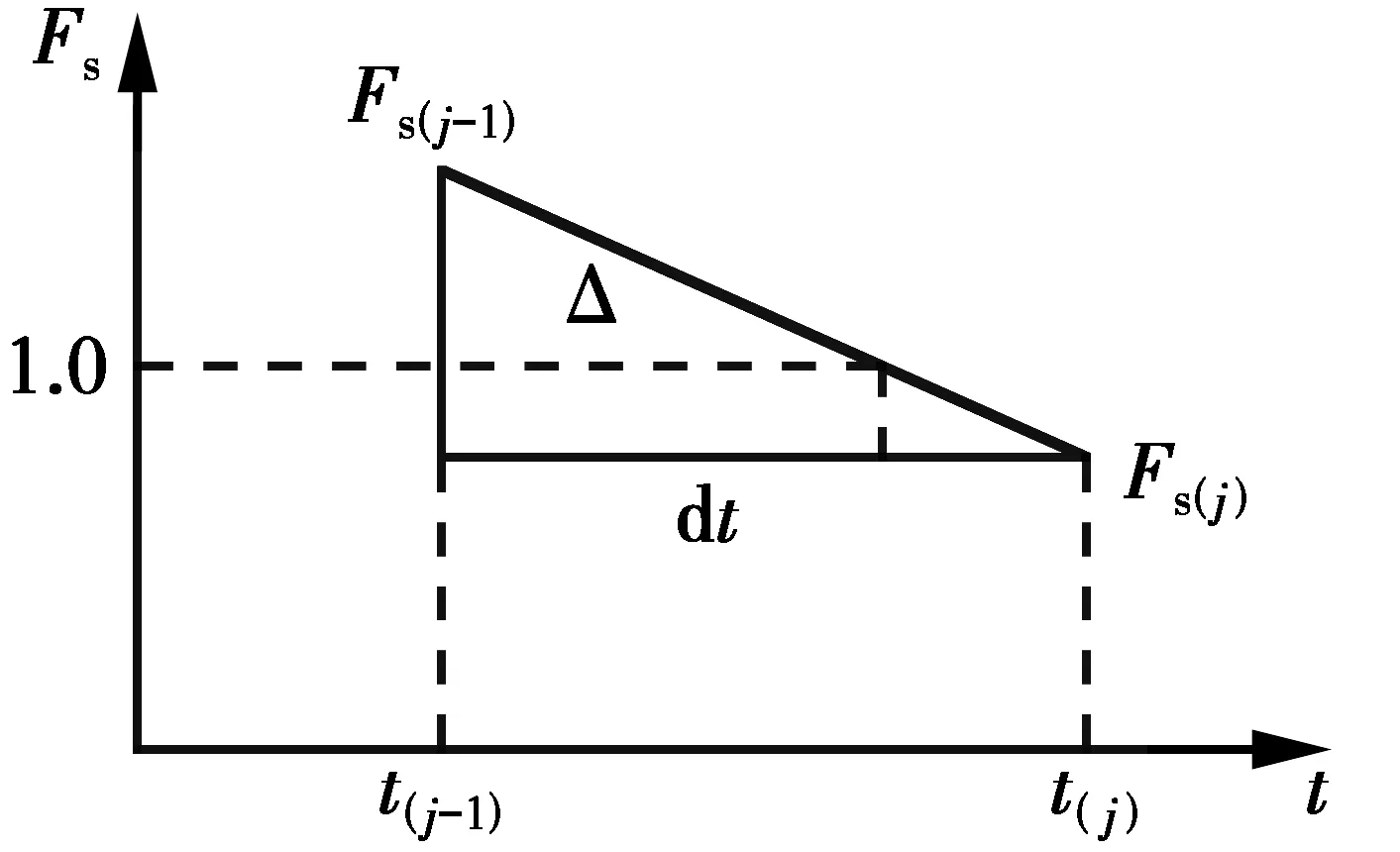
圖2　確定邊坡處于臨界滑動時刻的安全系數示意圖Fig.2　Determination of the time that slop begins to

由于假定地震加速度kv、kh在dt內為線性變化，故可依據第t(j-1)時刻的地震加速度(kv(j-1)、kh(j-1))和第t(j)時刻地震加速度(kv(j)、kh(j))求出第(t(j-1)+Δ)時刻(邊坡的臨界極限平衡狀態)的地震加速度(kv(j-1+△)、kh(j-1+Δ))。并將(kv(j-1+Δ)、kh(j-1+Δ))帶入式(9)，采用上述2.2.2節中的序列二次優化法對函數f(θ0，θh)進行了優化求解，校核邊坡最小安全系數是否為Fs(j-1+Δ)≈1.0(實際操作過程中，校核邊坡最小安全系數完全等于1.0非常困難，本文設置相對誤差限值為10-3，即認為在該時間步長內安全系數計算值符合要求。事實上，這樣處理所導致的安全系數計算值差異非常小，影響后續邊坡滑裂面參數取值也非常細微)。由此得到此刻邊坡開始滑動的滑裂面參數(θ0、θh)，并假定此后邊坡在地震作用下以此滑裂面保持不變。進一步對給定的加速度時程曲線中大于屈服加速度的部分進行二次積分求得對數螺旋線滑塊的總位移。

同時需要說明的是：對于某一特定邊坡而言，同時考慮某一特定地震波的水平向和豎直向加速度時，二者的臨界屈服加速度“組合”并不是唯一的。本文在選取兩者“組合”時，是依據該地震波時程范圍內兩者“組合”的第一個使邊坡達到臨界失穩狀態的時刻點。而非任意或者所有可能導致邊坡達到臨界狀態的“組合”。這樣實施的原因實際也符合僅考慮水平地震加速度-時程曲線時Newmark滑塊法計算邊坡永久位移的思想：在水平地震加速度-時程曲線上找到第一個使邊坡達到臨界失穩狀態的時間點，并認為邊坡的臨界滑裂面在出現永久位移的過程中不變。當然，實際中水平向和豎直向地震效應對邊坡的影響非常復雜，本文所選擇的計算策略僅為理想條件下的簡化，后續值得進一步研究。

2.3邊坡永久位移的計算

水平和豎向地震影響效應下，當邊坡恰好在第q時刻達到臨界失穩狀態，滑體內外功能處于動力平衡的方程式(3)變為

(13)

式中：(kv(q)、kh(q))為第q時刻的豎向和水平地震加速度。參數(θ0，θh)為第q時刻邊坡開始滑動的滑裂面參數，可通過編制優化程序求得。

由式(13)可得出地震作用下第q時刻的邊坡角加速度

(14)

在確定出邊坡的轉動角加速度以后，對給定的水平和豎向加速度時程曲線中大于水平和豎向臨界屈服加速度的部分進行二次積分，便可得到滑塊ABC的累計轉動滑移量，則邊坡坡腳的水平永久位移為

(15)

3算例與參數分析

3.1算例分析

僅輸入Northridge的水平地震波(圖7(a))采用You等[4]分析算例進行對比分析。本文方法得到的邊坡永久位移為4.20 cm，與原文計算結果4.20 cm一致，速度和位移時程曲線分別如圖3和圖4所示。同時，本文方法獲得的邊坡臨界滑裂面幾何參數和安全系數(θ0，θh，Fs)為(53.322，98.848，0.999)，與采用You等[4]所提方法進行重新編程運算所得的分析結果(θ0，θh，Fs)=(53.356，98.807，1.0)吻合，表明當只考慮水平向加速度時，本文方法蛻化為與前人方法兼容。

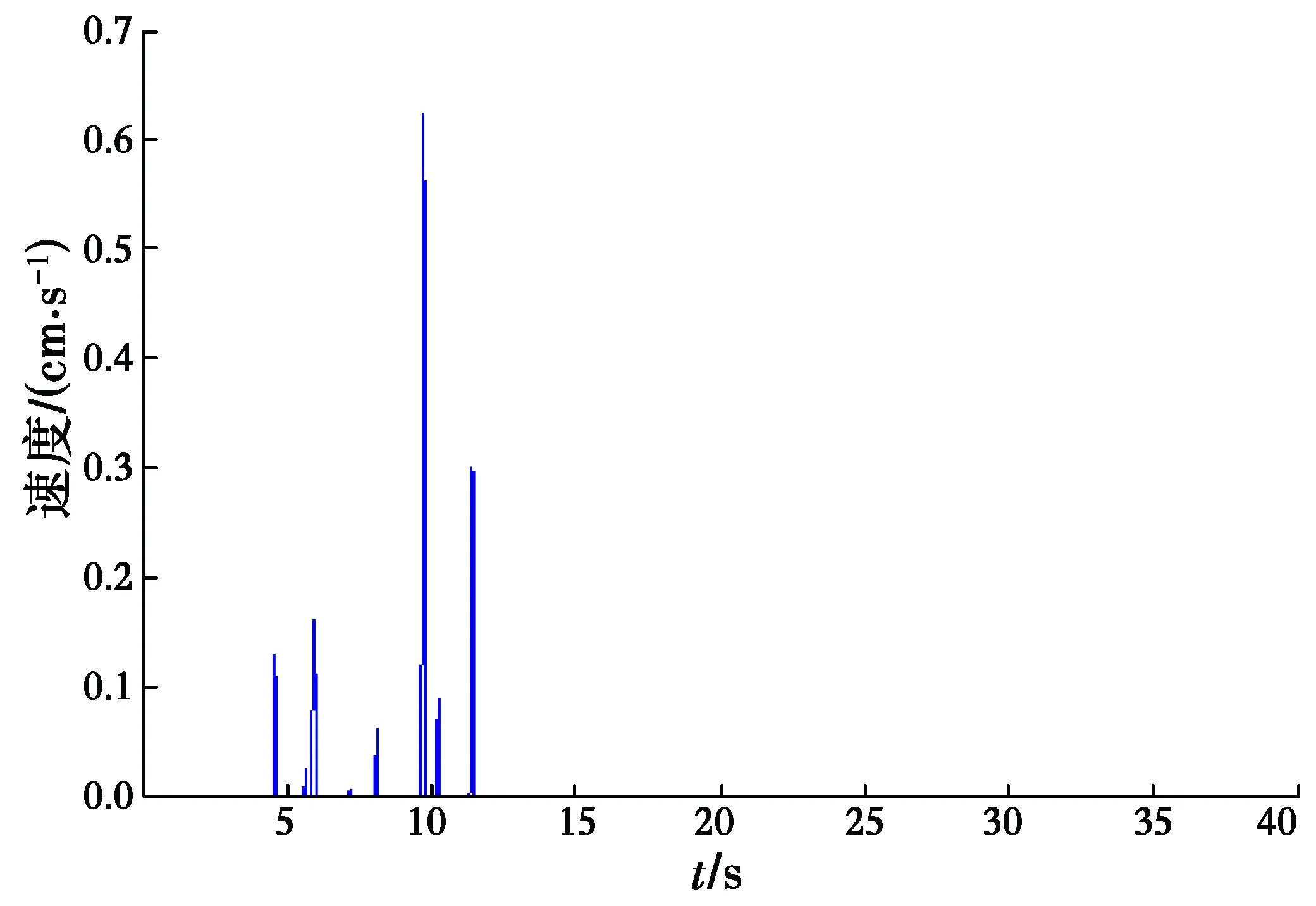
圖3　臨界失穩狀態下滑塊角速度-時程曲線Fig.3　Slop angular velocity-time

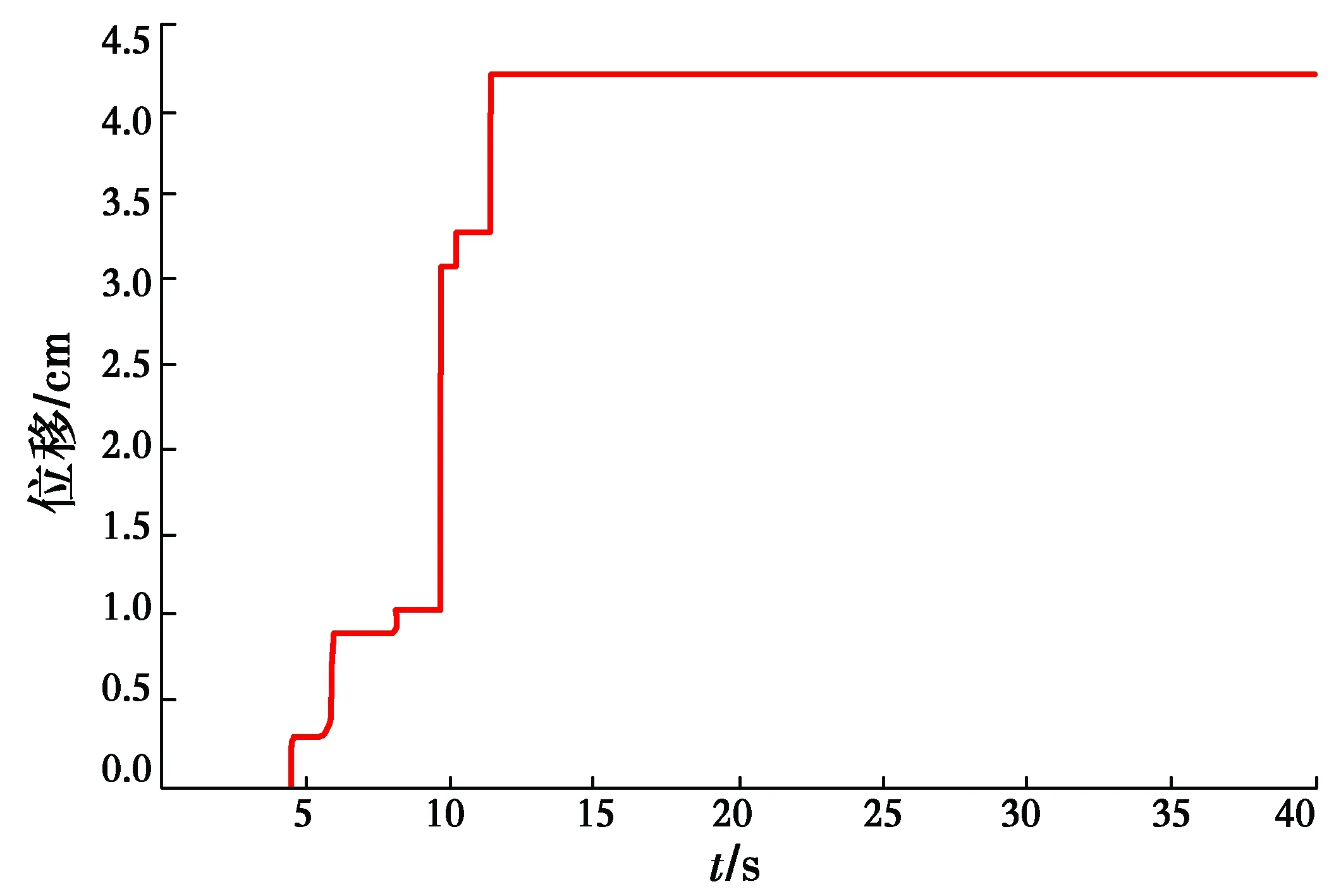
圖4　地震影響效應下邊坡永久位移-時程曲線Fig.4　Slop permanent displacement-time

3.2豎向地震效應的影響分析

同時輸入Northridge(1994)的水平和豎向地震波(圖7(a))，其豎向加速度峰值為155.98 cm/s2，時間步長取值為0.02。采用本文方法計算所得的邊坡角速度和位移時程圖如圖5和圖6所示。邊坡永久位移計算結果為4.48 cm，比只考慮水平地震效應的永久位移計算結果略有增大，表明忽略豎向地震可能使邊坡永久位移計算結果偏于不安全。

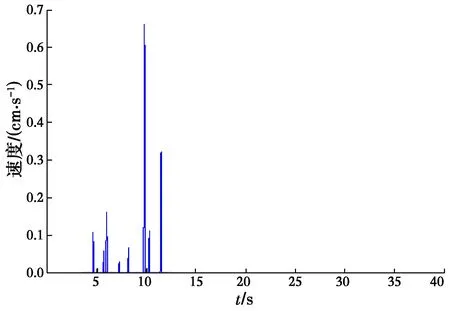
圖5　臨界失穩狀態下滑塊角速度-時程曲線Fig.5　Slop angular

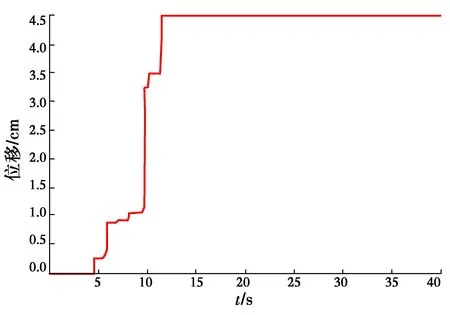
圖6　地震影響效應下邊坡永久位移-時程曲線Fig.6　Slop Permanent

由于天然地震具有強烈的隨機效應，不同的豎向地震波與水平地震波的疊加效應對邊坡永久位移影響不一樣。為更全面地分析豎向地震對邊坡永久位移的影響，本文中選取兩組具有不同頻譜特性的實測地震地面運動記錄(地震動的信息見表1，加速度時程如圖7所示)作用在傾角為45°、70°、90°邊坡上(邊坡參數見表2)，采取本文邊坡地震永久位移計算方法的計算結果見表3。

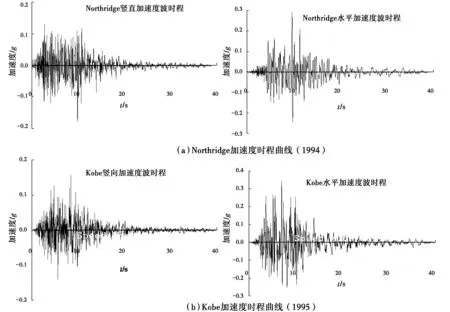
圖7　地震加速度時程曲線Fig.7　Acceleration time history of

地震名稱時間記錄地點震級PGA(g)(H)PGA(g)(V)震中距離/kmPref.Vs30/(m·s-1)DTNorthridge(a)1994-01-17Moorpark6.60.2920.15931.45405.200.02Kobe(b)1995-01-17Kakogawa6.90.3450.15824.20312.000.01

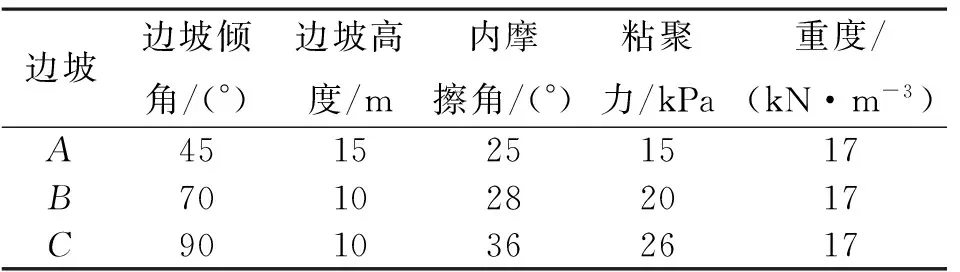
表2　邊坡參數

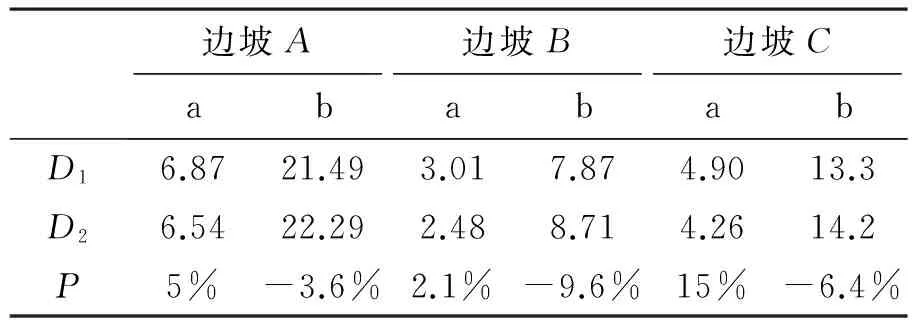
表3　邊坡永久位移

注：a、b分別代表Northridge 、kobe地震；D1代表水平與豎向地震疊加效應下邊坡的永久位移計算值；D2為僅考慮水平地震效應的邊坡永久位移計算值，P=(D1-D2)/D2×100%。

由表3可以看出地震a的水平與豎向地震疊加效應將使邊坡的永久位移計算值增加，地震b的水平與豎向地震疊加效應將使邊坡的永久位移計算值減小，不同地震記錄的豎向與水平地震的疊加效應不同；疊加效應最大可使邊坡的地震永久位移計算值增大超過15%，故豎向地震對邊坡永久位移的影響不可忽略。

4結論

1)結合極限分析上限分析法和強度折減技術，提出了一種基于水平與豎向地震加速度-時程曲線的邊坡地震永久位移計算改進方法。

2)探討了同水平向地震加速度-時程曲線成一定比例引入豎向地震加速度-時程曲線方法與基于實際水平與豎向地震加速度-時程曲線計算邊坡永久位移的差異。

3)不考慮豎向地震加速度-時程曲線的簡化條件下，與已有研究成果的對比計算證明本文方法可蛻化為與前人方法兼容。

4)分析了兩組具有代表性實測典型水平和豎向地震波記錄對邊坡永久位移的影響規律，計算結果表明：不同的豎向地震與水平地震的疊加效應不同，豎向地震對邊坡永久位移的影響不可忽略。

必須指出，本文在同時引入水平和豎向地震波影響效應進行地震永久位移計算時，采用了同時遍歷水平和豎向地震加速度時程曲線的方式，來獲求第一次達到臨界失穩的時刻節點(以邊坡最小安全系數第一次出現Fs=1.0來表征)；這一時刻節點即假定為邊坡開始滑動的時刻，并假定此后邊坡在地震作用下此滑裂面保持不變；獲得相應此刻的水平地震加速度值kh和豎向地震加速度值kv，進一步依據破壞模式假定獲得此時刻邊坡的滑裂面參數(θ0，θh) 。這種計算策略存在如下特點：

1)這種策略與時程曲線上時間間隔大小的選取有密切關系，當時間間隔取得越小時，計算耗時比較大；對于本文的簡單邊坡算例而言雖然可以接受，但對復雜邊界條件下邊坡的位移分析有待進一步研究；

2)本文在進行分析計算時，依據Newmark剛性滑塊位移計算的基本假定開展計算，認為邊坡第一次達到臨界極限平衡狀態的時刻節點為開始位移計算的初始時刻，此后邊坡在地震作用下以此滑裂面保持不變。且進一步依據所確定第一次滑動的滑動面參數(θ0，θh)通過兩次積分求得邊坡在整個地震過程中的永久位移。但對于某一特定邊坡而言，在同時輸入某一地震的水平和豎向地震加速度時程曲線進行分析時，引起邊坡失穩的水平和豎向地震加速度組合可能并不是唯一的。該組合型式與巖土邊坡幾何、抗剪強度特性等參數，以及分析采用破壞模式均有聯系。本文方法對于復雜邊坡地震永久位移分析方法的適用性還有待進一步深入。

參考文獻：

[1] NEWMARK N M.Effects of earthquakes on dams and embankments [J].Geotechnique,1965,15(2):139-160.

[2] CAI Z,BATHURST R J.Deterministic sliding block methods for estimating seismic displacements of earth structures [J].Soil Dynamics and Earthquake Engineering,1996,15(4):255-268.

[3] CHANG C J,CHEN W F,YAO J T P.Seismic displacements in slopes by limit analysis [J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1984,110(7):860-874.

[4] YOU L Z, MICHALOWSKI R L.Displacement charts for slopes subjected to seismic loads [J].Computers and Geotechnics,1999,25(1):45-55.

[5] MICHALOWSKI R L,YOU L.Displacements of reinforced slopes subjected to seismic loads [J].Journal of Geotechnical Geoenvironmental Engineering,2000,126(8):685-694.

[6] CONTI R,VIGGIANI G M B,CAVALLO S.A two-rigid block model for sliding gravity retaining walls [J].Soil Dynamics and Earthquake Engineering,2013,55(2):33-43.

[7] CEORGE G,ANASTASOPOULOS I,GARINI E.Geotechnical design with apparent seismic safety factors well-bellow 1 [J].Soil Dynamics and Earthquake Engineering,2014,57(2):37-45.

[8] JOORABCHIA A E,LIANGB R Y,LI L,et al.Yield acceleration and permanent displacement of a slope reinforced with a row of drilled shafts [J].Soil Dynamics and Earthquake Engineering,2014,57(3):68-77.

[9] KAVAZANJIAN E.Hanshin earthquake-reply [R].California:Geotechnical Bulletin Board, NSF Earthquake Hazard Mitigation Program,1995.

[10] MARIO P,RANDALL W J.A seismic landslide susceptibility rating of geologic units based on analysis of characteristics of landsides triggered by the 17 January, 1994 Northridge, California earthquake [J].Engineering Geology,2000,58(3/4):251-270.

[11] NOURIA H,FAKHER A,JONES C J F P.Evaluating the effects of the magnitude and amplification of pseudo-static acceleration on reinforced soil slopes and walls using the limit equilibrium Horizontal slices method [J].Geotextiles and Geomembranes,2008,26(4):263-278.

[12] LESCHINSKY D,LING H I,WANG J P,et al.Equivalent seismic coefficient in geocell retention systems [J].Geotextiles and Geomembranes,2009,27(1):9-18.

[13] VAHEDIFARD F,LESHCHINSKY D,MEEHAN C L.Displacement-based internal design of geosynthetic-reinforced earth structures subjected to seismic loading conditions [J].Geotechnique,2013,63(6):451-462.

[14] 劉紅帥，薄景山，劉德東.巖土邊坡地震穩定性分析研究評述[J].地震工程與工程振動,2005,25(1):164-171.

LIU H S,BO J S,LIU D D.Review on study of seismic stability analysis of rock-soil slopes [J].Earthquake Engineering and Engineering Vibration,2005,25(1):164-171. (in Chinese)

[15] 欒茂田，李湛,范慶來.土石壩擬靜力抗震穩定性分析與壩坡地震滑移量估算[J].巖土力學，2007,28(2):224-230.

LUAN M T,LI Z,FAN Q L.Analysis and evaluation of pseudo-static aseismic stability and seism-induced sliding movement of earth-rock dams [J].Rock and Soil Mechanics,2007,28(2):224-230. (in Chinese)

[16] LING H I，LESHCHINSKY D,YOSHIYUKI M.Soil slopes under combined horizontal and vertical seismic accelerations [J].Earthquake Engineering and Structural Dynamics,1997,26(12):1231-241.

[17] SIMONELLI A L,STEFANO P D.Effects of vertical seismic accelerations on slope displacements [C]//Proceedings of Fourth International Conference on Recent Advance in Geotechnical Earthquake Engineering and Soil Dynamics and Symposium in Honor of Professor W. D.Liam Finn.University of Missouri-Rolla,San Diego,California,2001:34-39.

[18] 黃建梁，王威中，薛宏交.坡體地震穩定性的動態分析[J].地震工程與工程振動,1997,17(4):113-122.

HUANG J L,WANG W Z,XUE H J.Dynamic analysis of seismic stability of slopes [J].Earthquake Engineering and Engineering Vibration,1997,17(4):113-122. (in Chinese)

[19] JACQUES I,JOSé D,JEAN-CLAUDE S.Effects of the vertical component of ground shaking on earthquake-induced landslide displacements using generalized Newmark analysis [J].Engineering Geology,2006,86:134-137.

[20] 李紅軍，遲世春，鐘紅,等.考慮時程豎向加速度的Newmark滑塊位移法[J].巖土力學,2007,28(11):2385-2390.

LI H J,CHI S C,ZHONG H,et al.Effects of dynamic shear strength and time-histories stress analysis on newmark sliding block analyses [J].Rock and Soil Mechanics,2006,27(11):1063-1068.(in Chinese)

[21] SAWICKI A,CHYBICKIEATL W.Influence of vertical ground motion on seismic-induced displacements of gravity structures [J].Computers and Geotechnics,2007,34:485-497.

[22] CHEN W F.Limit analysis and soil plasticity [M].Elsevier Science, Amsterdam,1975.

[23] 趙煉恒,李亮,楊峰,等.加筋土坡動態穩定性擬靜力分析[J].巖石力學與工程學報,2009,28(9):1904-1917.

ZHAO L H,LI L,YANG F,et al.Dynamic stability pseudo-static analysis of reinforcement soil slopes [J].Chinese Journal of Rock Mechanics and Engineering,2009,28(9):1904-1917. (in Chinese)

[24] BISHOP A W.The use of the slip circle in the stability analysis of slopes [J].Geotechique,1955,5(1):7-17.

[25] 龔純,王正林.MATLAB 語言常用算法程序集[M].北京: 電子工業出版社,2008.

[26] 唐高朋，趙煉恒，李亮，等.基于MATLAB的邊坡穩定性極限上限分析程序開發[J].巖土力學，2013，34(7)：2091-2098.

TANG G P,ZHAO L H,LI L,et al.Program development for slope stability using MATLAB software and upper bound limit analysis [J].Rock and Soil Mechanics,2013,34(7):2091-2098. (in Chinese)

[27] ZHAO L H,LI L,YANG F,et al.Upper bound analysis of slope stability with nonlinear failure criterion based on strength reduction technique [J].Journal of Central South University of Technology,2010,17(4):836-844.

(編輯王秀玲)

Upper bound analysis of seismic permanent displacement of soil slopes based on horizontal and vertical acceleration time-history curves

Wang Zhibin1,Tang Zuping2,Zhao Lianheng3,Cheng Xiao3

(1. School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201,Hunan,P.R. China;2. Shanghai Municipal Engineering Design Institute (Group) CO.,LTD-Shenzhen Branch, Shenzhen 518013,Guangdong,P.R. China; 3. School of Civil Engineering, Central South University, Changsha 410075,P.R. China)

Abstract:The dynamic stability of slopes is influenced by the horizontal and vertical earthquake forces. The traditional method of calculating the seismic permanent displacement does not take enough consideration about the vertical seismic effect. However, considering the combined effect of horizontal and vertical accelerations is more accord with the engineering practice. Based on the upper bound limit analysis and the model of Newmark’s rigid-plastic block, an approach for evaluating the permanent displacement of slopes based on the actual horizontal and vertical earthquake acceleration time-history curves is proposed. Three types of engineering slopes are studied to discuss the impact of two typical earthquake ground motions on seismic permanent displacement. The results show that: this method is compatible with the previous method without considering the vertical acceleration; the combined effect of horizontal and vertical accelerations is different for various earthquake records, and the influence of vertical acceleration on the permanent slope displacement cannot be ignored.

Keywords:slope; seismic permanent displacement; acceleration time-history curves; Newmark’s method; upper bound limit analysis

doi:10.11835/j.issn.1674-4764.2016.02.005

收稿日期：2014-11-18

基金項目：國家自然科學基金(51208522)；湖南省科學技術廳科技項目(2012SK3231、2012TT2039)；貴州省交通廳科技項目(2013-122-005)

作者簡介：王志斌(1975-)，男，博士，主要從事路基路面工程研究，(E-mail)71496933@qq.com。

中圖分類號：TU435

文獻標志碼：A

文章編號：1674-4764(2016)02-0035-09

趙煉恒(通信作者)，男，博士(后)，副教授，博士生導師，(E-mail)zlh8076@163.com。

Received:2014-11-18

Foundation item：National Natural Science Foundation of China (No.51208522); Hunan Provincial Department of Science and Technology Foundation (No.2012SK3231,2012TT2039); Guizhou Provincial Department of Transportation Foundation (No.2013-122-005)

Author brief：Wang Zhibin (1975-), PhD, main research interests: subgrade and pavement engineering, (E-mail) 71496933@qq.com.

Zhao Lianheng (corresponding author), postdoctor, associate professor, PhD supervisor, (E-mail) zlh8076@163.com.