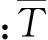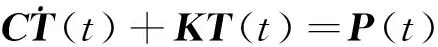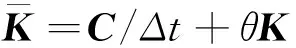三維軸對稱功能梯度材料瞬態熱傳導問題的自然單元法

李慶華,陳莘莘,徐青

(華東交通大學 土木建筑學院， 南昌 330013)

?

三維軸對稱功能梯度材料瞬態熱傳導問題的自然單元法

李慶華,陳莘莘,徐青

(華東交通大學 土木建筑學院， 南昌 330013)

摘要：為了更有效地求解三維軸對稱功能梯度材料瞬態熱傳導問題，對無網格自然單元法應用于此類問題進行了研究，并發展了相應的計算方法。基于幾何形狀和邊界條件的軸對稱性，三維的軸對稱問題可降為二維平面問題。為了簡化本質邊界條件的施加，軸對稱面上的溫度場采用自然鄰近插值進行離散。功能梯度材料特性的變化由高斯點的材料參數進行模擬。時間域上，采用傳統的兩點差分法進行離散求解，進而得到瞬態溫度場的響應。數值算例結果表明，提出的方法是行之有效的,理論及方法不僅拓展了自然單元法的應用范圍，而且對三維軸對稱瞬態熱傳導分析具有普遍意義。

關鍵詞：自然單元法；軸對稱；功能梯度材料；瞬態熱傳導

功能梯度材料是通過特定的材料制備工藝將不同性能的兩種或兩種以上材料按一定的設計規律組合起來的新型非均勻復合材料[1]。功能梯度材料的最大特點是材料參數的連續性，完全避免了層合復合材料的材料參數在層層之間的間斷面處不連續的問題，提高了材料強度和耐熱性。因此，功能梯度材料在航空、航天及核反應堆等高溫環境中具有廣泛的應用潛力，對功能梯度材料的熱力學行為進行研究十分必要[2-5]。然而，相對于二維平面問題，目前對于三維軸對稱功能梯度材料瞬態熱傳導問題的數值方法研究相對較少[6-8]。

自然單元法[9-10]是一種新興的數值分析方法，因其獨特的優勢，得到了國內外許多學者的極大關注[11-15]。這種方法基于離散節點的Voronoi圖和Delaunay三角化幾何結構，采用自然鄰近插值構造全域近似函數和試函數。自然鄰近插值方案構造簡單，不涉及到復雜的矩陣求逆運算，而且不需要任何人為參數，從而避免了無單元伽遼金法中由于不確定的影響半徑造成的影響域計算的不確定性。此外，自然單元法的形函數滿足插值性質，可以準確地施加本質邊界條件，無需其他無網格法類似的特殊處理過程。自然單元法已經被成功地應用于很多領域，但目前尚未見到三維軸對稱熱傳導分析的無網格自然單元法的研究成果。

為了進一步拓展自然單元法的應用范圍，本文基于加權殘值法詳細推導了三維軸對稱功能梯度材料瞬態熱傳導分析的自然單元法理論公式，并給出了其詳細的數值實現過程。在此基礎上，采用FORTRAN自編了相關的計算程序。最后，通過典型算例的計算和對比分析，不僅驗證了自然單元法應用于三維軸對稱功能梯度材料瞬態熱傳導分析的有效性和合理性，并且討論了梯度參數的變化對計算結果的影響。

1自然鄰近插值

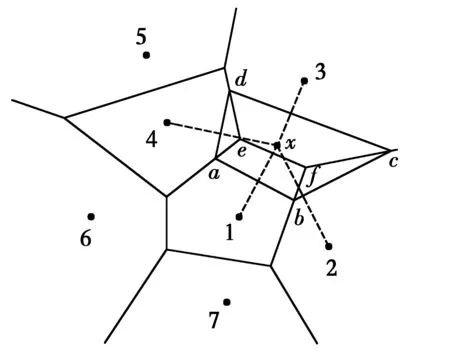
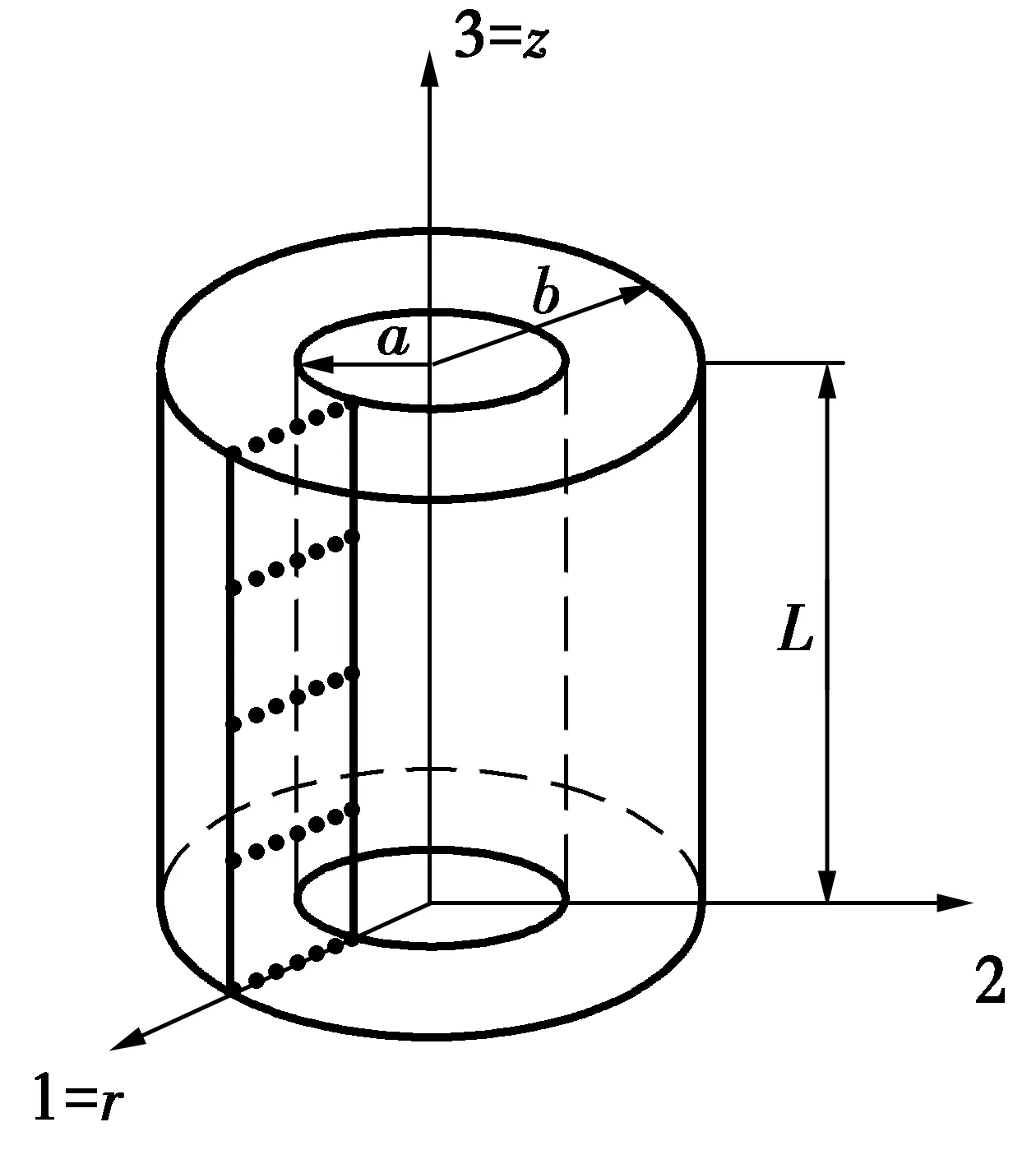
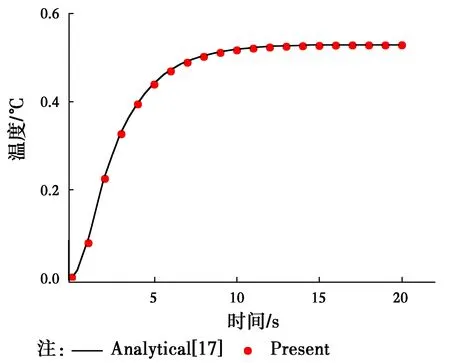
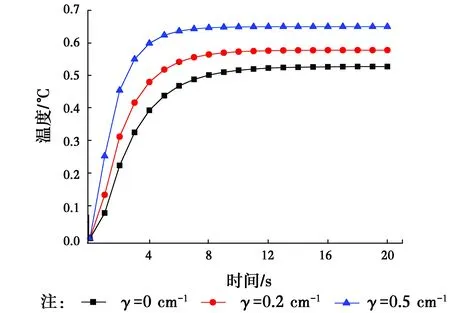
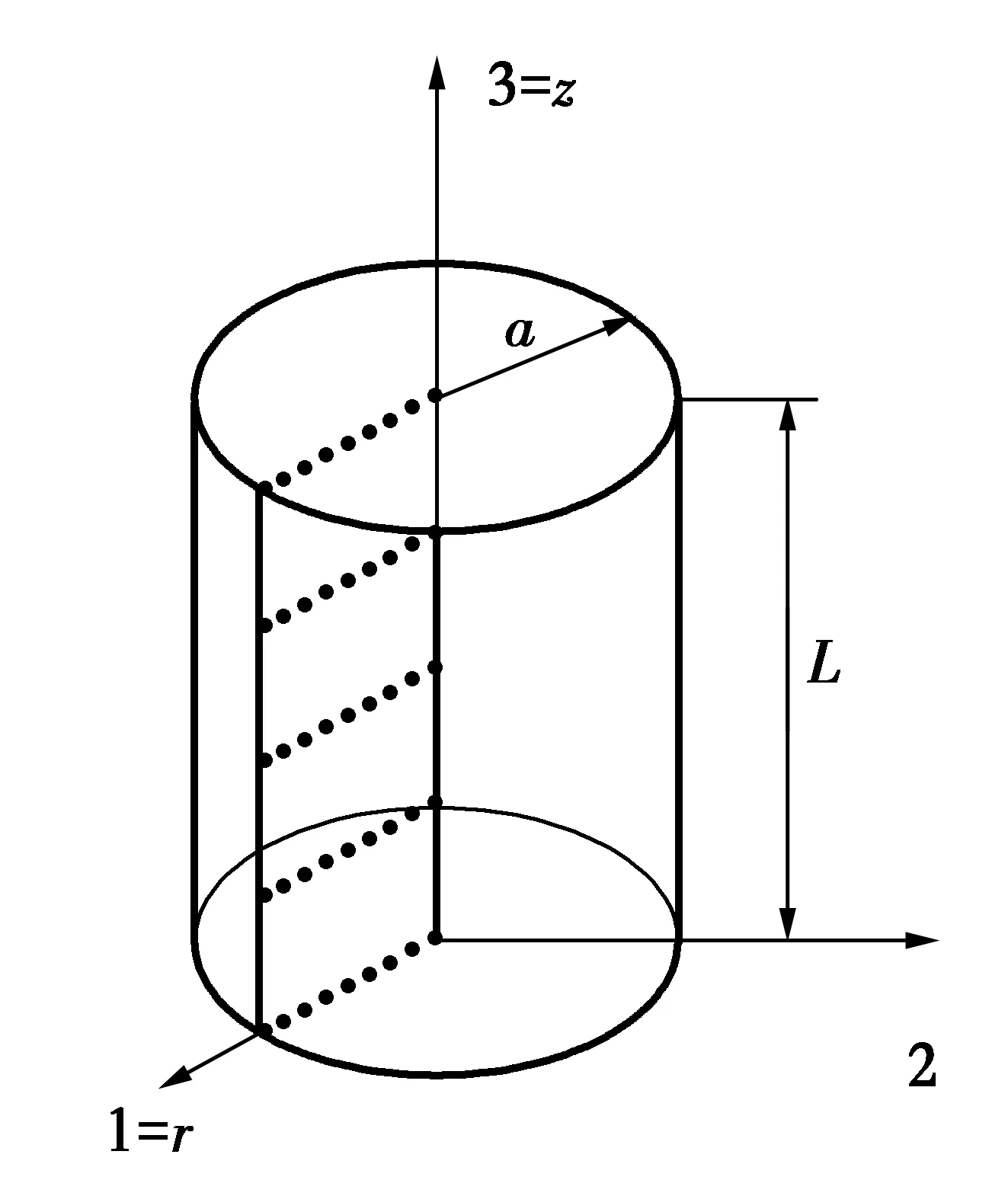
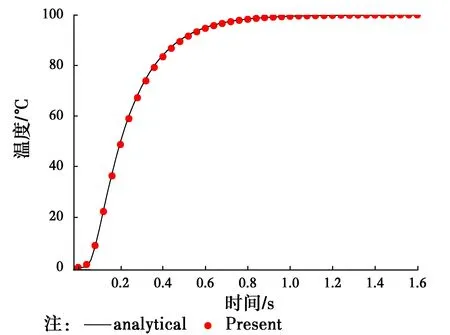
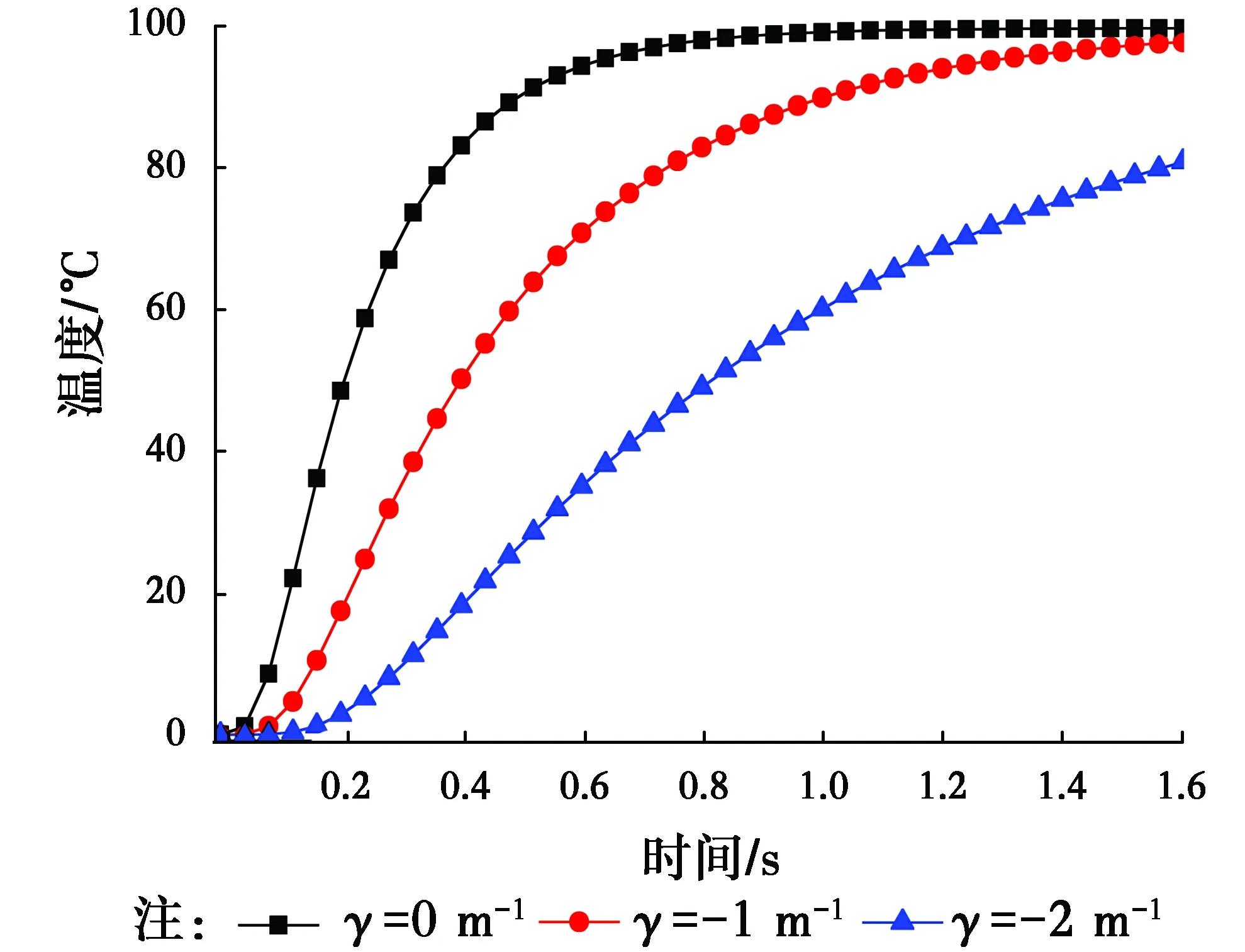
TI={x∈R2:d(x,xI)

(1)

式中:d(x,xI)為點x與節點xI的距離。

為確定Sibson插值形函數，定義二次Voronoi結構為

(2)

在幾何意義上，TIJ實際上是以節點xI為最近點，節點xJ為次近點的空間點位置的集合。圖1所示為平面7個節點的Voronoi結構和待插點x的二次Voronoi結構。

構造出插值點x的一次和二次Voronoi結構后，插值點x的形函數及其導數可以寫為[9]

(3)

(4)

式中:AI(x)表示插值點x的二次Voronoi結構TxI的面積;A(x)表示插值點x的一次Voronoi結構Tx的面積，即TxI的總和。

圖1　點x的一次和二次Voronoi結構Fig.1　First-order and second-order Voronoi cells about

定義了各節點的插值函數后，點x的溫度函數類似于有限元法可寫為

(5)

式中:TI(I=1,2,…,n)是計算點x周圍自然鄰節點I的節點溫度。

2控制方程的弱形式及其離散化

在三維軸對稱瞬態熱傳導問題中，空間參量只有半徑r和軸向參量z。在軸對稱面Ω上，Γ1和Γ2分別表示問題域的本質邊界和自然邊界。空間的溫度分布應該滿足下面的偏微分方程

(6)

式中：T(x,t)為瞬態溫度場;t為時間，Q(x,t)為單位體積的內部熱源;k(x)為熱傳導系數，α(x)為熱擴散系數。對應的邊界條件和初始條件為

(7a)

(7b)

(7c)

式(6)的等效積分形式的伽遼金提法可表示為

(8)

式中:δT代表真實溫度的變分。對式(8)進行分部積分并考慮式(7b)，可得

(9)

由于只對空間域進行離散，求解域Ω內的試函數Th(x,t)可由式(5)表示為

(10)

將空間離散后的溫度表達式(10)代入式(9)，并考慮到δTI的任意性，就可以得到最終的線性常微分方程組

(11)

式中:

(12a)

(12b)

(12c)

3時間積分方案

經過對空間域的無網格自然單元法離散，已將溫度場的偏微分方程轉化為一組以時間t為獨立變量的一階線性常微分方程組。本文中采用傳統的兩點差分法[16]對時間域進行離散。

圖2　空心圓筒的節點布置方案Fig.2　Nodal distribution for a hollow

一般情況下，兩點差分格式可以寫成

(13)

式中:Δt是時間步長，θ為時間加權系數。將上式代入式(11)，經過整理后可得到

(14)

式中

(15a)

(15b)

通過從0到1更改參數θ，有關這個系列方法都可以得到。本文取θ=2/3。

4數值算例

4.1空心圓筒

有一無限長的功能梯度空心圓筒，其內半徑a=8×10-2m，外半徑b=10×10-2m，如圖2所示。為了該問題的分析，截取長L=2×10-2m的一段，且上下兩截面視為絕熱面。內表面溫度T0=0 ℃，外表面溫度T1=1 ℃，初始溫度給定為零。計算中，均勻布置45(9×5)個節點，時間步長取Δt=0.5s。

假設熱傳導系數與熱擴散系數沿徑向指數變化，即

(16)

式中:k0=17W/m· ℃，α0=1.7×10-5m2/s。為了檢驗本文方法的有效性，取k=k0和α=α0計算得到了均質材料(γ=0)的情況下空心圓筒在r=9cm處溫度隨時間的變化，如圖3所示。為了進行對比，圖3中還給出了相應的解析解[17]。可以看出，本文方法與解析解精確吻合，證明本文方法是有效的。

圖3　均質空心圓筒在r=9.0 cm處溫度隨時間的變化Fig.3　Time variations of the temperature at r=9.0 cm in the hollow cylinder with homogeneous material

為了研究梯度參數γ對溫度變化的影響，采用自然單元法計算得到了γ=0.0，γ=0.2 cm-1和γ=0.5 cm-1時空心圓筒在r=9 cm處溫度隨時間的變化，如圖4所示。正如我們期待的，在圖4中，隨著梯度參數的增加，材料導熱性增加，對應的溫度也隨之上升。

圖4　功能梯度空心圓筒在r=9.0 cm處溫度隨時間的變化Fig.4　Time variations of the temperature at r=9.0 cm in a functionally graded hollow

4.2實心圓筒

為了進一步驗證本文數值方法的有效性，考慮如圖5所示的一無限長的功能梯度實心圓筒，其半徑a=1 m。截取長L=1 m的一段，外表面溫度T=100 ℃，其余邊界絕熱，初始溫度給定為零。計算中，沿徑向均勻布置9個節點，沿軸向均勻布置5個節點，時間步長取Δt=0.02 s。

圖5　實心圓筒的節點布置方案Fig.5　Nodal distribution for a full cylinder

假設熱傳導系數與熱擴散系數沿徑向指數變化，即

(17)

式中:k0=1.0 W/m·℃，α0=1.0 m2/s。與前一算例類似，取k=k0和α=α0對均質材料(γ=0)情況下的實心圓筒進行了瞬態熱傳導分析。圖6給出了均質實心圓筒在對稱軸處的溫度隨時間變化的本文數值解與解析解[17]的比較，可以看出采用自然單元法的數值解與解析解吻合很好，說明自然單元法在三維軸對稱瞬態熱傳導分析中可以取得很高的計算精度。

圖6　均質實心圓筒對稱軸處溫度隨時間的變化Fig.6　Time variations of the temperature on the axis of the full cylinder with homogeneous material

為了進一步研究梯度參數γ對溫度變化的影響，圖7給出了γ=0.0，γ=-1 m-1和γ=-2 m-1時采用自然單元法計算得到的實心圓筒在對稱軸處溫度隨時間的變化。顯然，圖7也反映了這種溫度隨著梯度參數增加而上升的現象。

圖7　功能梯度實心圓筒在對稱軸處溫度隨時間的變化Fig.7　Time variations of the temperature on the axis of a functionally graded full cylinder

5結論

作為介于有限元法與無網格法之間的一種數值方法，自然單元法的節點影響域是由節點的Voronoi結構所規定的自然相鄰關系給出，不受人為參數的影響，具有其他無網格法不可比擬的優越性。根據三維軸對稱功能梯度材料瞬態熱傳導方程及其邊界條件，利用加權殘值法，選取自然鄰近插值對軸對稱面上的溫度場進行離散，首次詳細推導了三維軸對稱功能梯度材料瞬態熱傳導問題的自然單元法計算公式，并編制了相應的FORTRAN計算程序。本文分析和算例求解結果表明，采用自然單元法求解三維軸對稱功能梯度材料瞬態熱傳導問題是可行的，具有精度高和穩定性好的優點。本文方法還可以容易地推廣到三維軸對稱功能梯度材料熱彈性問題的求解計算。

參考文獻：

[1] 張靜華，魏軍楊. DQ法求解FGM Levinson梁的靜態彎曲問題[J]. 華東交通大學學報, 2014, 31(3): 80-87.

ZHANG J H, WEI J Y. Static bending solution of functionally graded material Levinson beams based on differential quadrature method [J]. Journal of East China Jiaotong University, 2014, 31(3): 80-87. (in Chinese)

[2] WANG H, QIN Q H, KANG Y L. A meshless model for transient heat conduction in functionally graded materials [J]. Computational Mechanics, 2006, 38: 51-60.

[3] 藍林華，富明慧，程正陽. 功能梯度材料瞬態熱傳導問題的降維精細積分法[J]. 固體力學學報, 2010, 31(4): 406-410.

LAN L H, FU M H, CHENG Z Y. Decrement-dimensional precise time integration of 2D transient heat conduction equation for functionally graded materials [J]. Chinese Journal of Solid Mechanics, 2010, 31(4): 406-410. (in Chinese)

[4] 陳建橋，丁亮. 功能梯度材料瞬態熱傳導問題的MLPG方法[J]. 華中科技大學學報(自然科學版), 2007, 35(4): 119-121.

CHEN J Q, DING L. A MLPG method of transient heat transfer in FGMs [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2007, 35(4): 119-121. (in Chinese)

[5] 李慶華，陳莘莘，薛志清，等. 基于自然元法和精細積分法的功能梯度材料瞬態熱傳導問題求解[J]. 計算機輔助工程, 2011, 20(3): 25-28.

LI Q H, CHEN S S, XUE Z Q, et al. Transient heat conduction solution to functionally graded materials based on natural element method and precise integration method [J]. Computer Aided Engineering, 2011, 20(3): 25-28. (in Chinese)

[6] LI Q H, CHEN S S, ZENG J H. A meshless model for transient heat conduction analyses of 3D axisymmetric functionally graded solids [J]. Chinese Physics B, 2013, 22: 120204.

[7] SLADEK J, SLADEK V, HELLMICH C h, et al. Heat conduction analysis of 3D axisymmetric and anisotropic FGM bodies by meshless local Petrov-Galerkin method [J]. Computational Mechanics, 2007, 39: 323-333.

[8] SLADEK J, SLADEK V, KRIVACEK J, et al. Local BIEM for transient heat conduction analysis in 3D axisymmetric functionally graded solids [J]. Computational Mechanics, 2003, 32: 169-176.

[9] SUKUMAR N, MORAN T, BELYTSCHKO T. The natural element method in solid mechanics [J]. International Journal for Numerical Methods in Engineering, 1998, 43(5): 839-887.

[10] SUKUMAR N, MORAN B. C1 natural neighbour interpolation for partial differential equations [J]. Numerical Methods for Partial Differential Equations, 1999, 15(4): 417-447.

[11] 江濤，章青. 直接增強自然單元法計算應力強度因子[J]. 計算力學學報, 2010, 27(2): 264-269.

JIANG T, ZHANG Q. Computing stress intensity factors by enriched natural element method [J]. Chinese Journal of Computational Mechanics, 2010, 27(2): 264-269. (in Chinese)

[12] 張勇，易紅亮，談和平. 求解輻射導熱耦合換熱的自然單元法[J]. 工程熱物理學報, 2013, 34(5): 918-922.

ZHANG Y, YI H L, TAN H P. Natural element method for coupled radiative and conductive heat transfer [J]. Journal of Engineering Thermophysics, 2013, 34(5): 918-922. (in Chinese)

[13] 董軼，馬永其，馮偉. 彈性力學的雜交自然單元法[J]. 力學學報, 2012, 44(3): 568-575.

DONG Y, MA Y Q, FENG W. The hybrid natural element method for elasticity [J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(3): 568-575. (in Chinese)

[14] 曾祥勇，朱愛軍，鄧安福. Winkler地基上厚板分析的自然單元法[J]. 固體力學學報, 2008, 29(2): 163-169.

ZENG X Y, ZHU A J, DENG A F. Natural element method for analysis of thick plates lying over Winkler foundation [J]. Chinese Journal of Solid Mechanics, 2008, 29(2): 163-169. (in Chinese)

[15] 周書濤，劉應華，陳莘莘. 基于自然單元法的極限上限分析[J]. 固體力學學報, 2012, 33(1): 39-47.

ZHOU S T, LIU Y H, CHEN S S. Upper-bound limit analysis based on natural element method [J]. Chinese Journal of Solid Mechanics, 2012, 33(1): 39-47. (in Chinese)

[16] CHEN L, LIEW K M. A local Petrov-Galerkin approach with moving Kriging interpolation for solving transient heat conduction problems [J]. Computational Mechanics, 2011, 47: 455-467.

[17] CARSLAW H S, JAEGER J C. Conduction of heat in solids [M]. Oxford: Clarendon Press, 1959.

(編輯胡玲)

Natural element method for transient heat conduction analyse of 3D axisymmetric functionally graded solids

Li Qinghua, Chen Shenshen, Xu Qing

(School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, P.R. China)

Abstract:In order to solve the transient heat conduction problems in three-dimensional (3D) axisymmetric continuously nonhomogeneous functionally graded materials (FGMs) more effectively, a novel numerical method based on the meshless natural element method is proposed. Axial symmetry of geometry and boundary conditions helps to transform the 3D axisymmetric problem into a two-dimensional (2D) prolem. In order to simplify the imposition of the essential boundary conditions, the natural neighbour interpolation is adopted to discretize the temperature field within the cross section. The variations of functionally graded material properties are simulated by employing proper material parameters at Gauss points. The spatially discretized heat conduction equation is solved numerically with the traditional two-point difference technique in the time domain. The present method not only broadens the application scope of the natural element method, but also will be generally available to transient heat conduction analyses of 3D axisymmetric solids.

Keywords:natural element method; axisymmetric; functionally graded materials; transient heat conduction

doi:10.11835/j.issn.1674-4764.2016.02.009 10.11835/j.issn.1674-4764.2016.02.010

收稿日期：2015-11-15

基金項目：國家自然科學基金(21466012)；江西省教育廳項目(KJLD14041).

作者簡介：李慶華(1976-)，女，主要從事數值傳熱學研究，(E-mail) jessylqh@126.com。

中圖分類號：TP301.6

文獻標志碼：A

文章編號：1674-4764(2016)02-0069-06

Received:2015-11-15

Foundation item：National Natural Science Foundation of China (No.21466012); Foundation of Jiangxi Educational Committee (No.KJLD14041)

Author brief：Li Qinghua(1976-), main research interest: numerical heat transfer, (E-mail) jessylqh@126.com.