汽車縱向主動避撞DRV安全距離模型

袁朝春，李道宇，吳　飛，劉逸群，張龍飛

(江蘇大學 汽車與交通工程學院，江蘇 鎮江　212013)

?

汽車縱向主動避撞DRV安全距離模型

袁朝春，李道宇，吳飛，劉逸群，張龍飛

(江蘇大學 汽車與交通工程學院，江蘇 鎮江212013)

摘要：分析了駕駛員因素、交通路況因素和車輛制動性能因素對安全距離的影響，并在此基礎上建立了DRV安全距離模型。應用Prescan仿真平臺對DRV安全距離模型進行效果驗證。結果表明：DRV安全距離模型能同時兼顧駕駛安全和道路使用率，基于此模型計算的報警安全距離和自動制動安全距離更加合理。

關鍵詞：車輛工程；主動避撞；安全距離； Prescan仿真平臺

隨著汽車保有量的快速增長，道路交通安全問題已經成為各國政府和社會廣泛關注的重要問題。美國國家高速公路安全委員會(NHTSA)的調研結果表明[1]:在道路交通致死事故中，因駕駛員過失造成的約占90%，而因車輛故障造成的僅占約3%。盡管可采用越來越多的被動安全技術(如安全氣囊、安全帶、行人保護和吸能車體等)減輕事故的傷害程度，但引發交通事故產生的原因未得到根本解決。通過對自車(主動避撞車)縱向運動狀態的控制，使自車與前方目標保持合適的距離或自動維持自車的某種運動狀態可以實現汽車的縱向主動避撞。

汽車縱向避撞系統通過降低車速和保持足夠的車間距離來實現行車安全目標。而智能電動轉向系統是通過轉向操作把自車和交通參與者的橫向距離維持在一個合理的范圍內。

由于道路容量與車速成正比，而與車間距離成反比，過多地降低車速和加大車間距離會導致道路交通效率的降低。因此，應用于汽車避撞系統的安全距離模型必須兼顧行車安全和道路交通效率兩方面的要求，并應有所側重。

國內外的學者們提出了多種駕駛安全距離模型，利用安全距離的實時計算結果與實際車間距離之間的關系進行行車安全狀態的判斷，主要有基于制動過程運動學分析的安全距離模型[2]、基于車間時距的安全距離模型[3-4]、駕駛員預瞄安全距離模型[5]。現有安全距離模型主要是以制動系統和發動機為控制對象，應用于汽車主動避撞研究時存在準確性較低、不能適應復雜多變交通環境的需要、某些關鍵參數在現有技術條件下不易獲得、實用性較低及對駕駛員主觀感受因素考慮不足等幾方面的問題。

影響車輛安全距離的主要因素有下列幾個：車輛制動系統性能、道路交通信息狀況、駕駛員反應能力，而現有的安全距離模型還不能同時反映這3個方面。

本研究綜合考慮駕駛員因素、交通路況因素和車輛制動性能因素，建立了DRV安全距離模型，并通過Prescan仿真平臺對DRV安全距離模型的有效性進行驗證。

1現有安全距離模型分析

現有安全距離模型中，比較有代表性的有2個[5-7]：

1) Hideo Araki安全距離模型

(1)

其中：dw為安全車距；v1，a1為自車當前的速度和加速度；v2，a2為前方交通參與者的速度和加速度。此模型考慮了前、后車的運動關系，并且根據前、后車當前的運動狀態分為兩種情況：當自車速度相對比較小時，最終制動結束的條件為兩車速度相等；當自車(后車)相對速度比較大時，制動結束條件為兩車的速度均為0。可以看出：該模型沒有考慮駕駛員和道路狀況因素對安全距離的影響。

2) 馬自達公司安全距離模型

(2)

其中：dw為安全車距；v1，a1代表自車(后車)當前的速度和加速度；v2，a2代表前方交通參與者的速度和加速度；td為駕駛員反應時間；tbrk為制動系統響應時間；d0為兩車安全距離。

該模型基本思想：當前方交通參與者(或障礙物)以穩定的制動減速度減速時，后車傳感器發現并開始向系統傳達這種信息；當前后距離低于制動距離時系統給制動器發出指令，后車開始減速，最后兩者相對速度為0，此時兩車相距d0。模型中系統延遲時間和后車減速時間這2個參數是通過大量實驗測定的，該模型中前、后兩車的加速度分別取不同值，可以看出該模型沒有考慮道路狀況對車輛安全距離的影響。

2DRV安全距離模型

綜合考慮駕駛員因素(driver factor)、交通路況因素(road factor)和車輛制動性能因素(vehicle factor)建立DRV安全距離模型。

2.1輪胎-路面附著系數辨識

根據Luis Alvarez 等[8-9]的研究成果，輪胎-路面附著系數和車速及輪胎滑移率有關，其辨識函數如式(3)所示。

(3)

式中：μ為輪胎-路面附著系數；λ為輪胎滑移率；v為車輛行駛速度；pi(i=1,2,…,5)為常數(同一車型參數固定)。表1為某車型pi的常數取值。表2為常見輪胎-路面附著系數。

表1　某車型pi常數取值

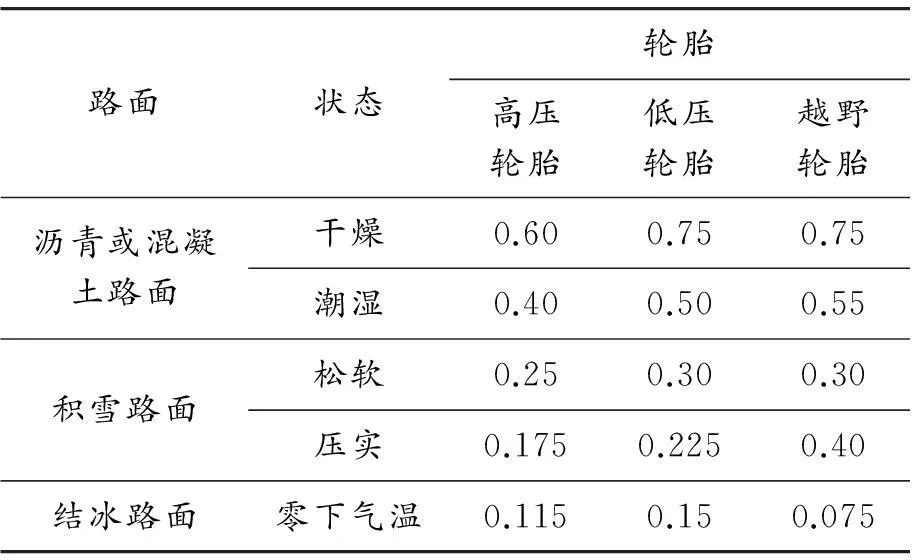
表2　常見輪胎-路面附著系數

2.2駕駛員制動反應時間建模

駕駛員駕駛能力、疲勞狀態和環境因素對車輛制動安全距離起主要影響，形成對駕駛員反應時間進行評估的狀態向量：X=(X1,X2,X3)，其中0≤Xi≤100(i=1,2,3)。

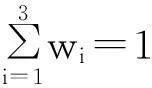
采用綜合加權法構造駕駛員反應時間影響評估函數：

(4)

其中Tnormal-d=1.25s，為普通駕駛員在正常狀態下的制動反應時間。

2.3最大制動減速度建模

車輛實際制動能力受車輛性能參數、輪胎-路面附著系數和實際駕駛環境等的影響。假設車輛制動系統可以發揮道路的最大制動效能，則最大制動減速度主要受輪胎-路面附著系數和實際駕駛環境的影響。圖1為車輛受力分析情況。

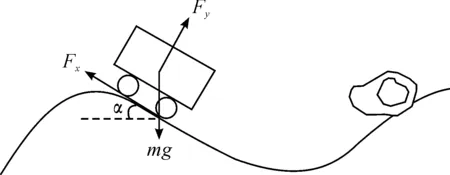
圖1　車輛受力分析情況

在車輛制動系統可以發揮最大制動效能時，Fx=μmgcosα，式中：μ為輪胎-路面附著系數；m為整車載荷；α為摩擦力和水平方向夾角。

經過計算可知：在不同駕駛環境下的車輛最大制動減速度為

(5)

式中ar-max為最大制動減速度。

2.4DRV安全距離模型建模

在現有車輛制動安全距離模型基礎上[10-11]建立DRV模型：

(6)

(7)

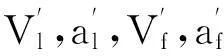
綜上可以看出，目前所采用的車輛制動安全距離計算模型沒有考慮駕駛員、車輛制動性能和駕駛環境的影響，模型的實用性和通用性受到明顯制約。

建立DRV安全距離模型：

其中：Dw，Dbr分別為追尾碰撞報警距離和自動制動距離； Vr，ar-max分別為后(自)車速度和最大制動減速度；Vf，af分別為前車的速度和加速度；Tr-d為后(自)車駕駛員制動反應時間；Tr-b為后(自)車制動系統響應時間；Tbr為自動制動時的制動時間。

把式(3)、(4)分別代入式(8)、(9)得

(10)

(11)

3DRV安全距離模型效果驗證

本次仿真基于Prescan仿真軟件進行。

假設：自車駕駛員駕駛經驗不足，且為疲勞駕駛狀態，駕駛視線不是很好，自車行駛道路為下坡(坡度為30%)，當前行駛速度為10 m/s，滑移率為20%,制動系統響應時間為0.2 s，前車因故障拋錨在道路中間。

自車駕駛員反應時間評價狀態向量為X=(75,50,50)，其對應的權重分別為w=(0.4,0.4,0.2)。

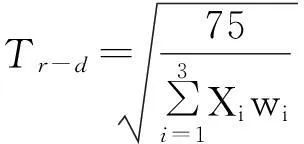
常用兩類模型和DRV模型在該工況下的報警安全距離和自動制動安全距離如圖2～4所示。

將假設條件輸入Prescan并建立模擬場景，得到DRV安全距離模型的報警安全距離為31.33 m，自動制動安全距離為17.33 m，如圖2所示。Hideo Araki模型的報警安全距離與自動制動安全距離如圖3所示。馬自達模型的報警安全距離如圖4所示。在該工況下，常用的兩類模型和DRV模型的報警安全距離和自動制動安全距離的理論值如表3所示。

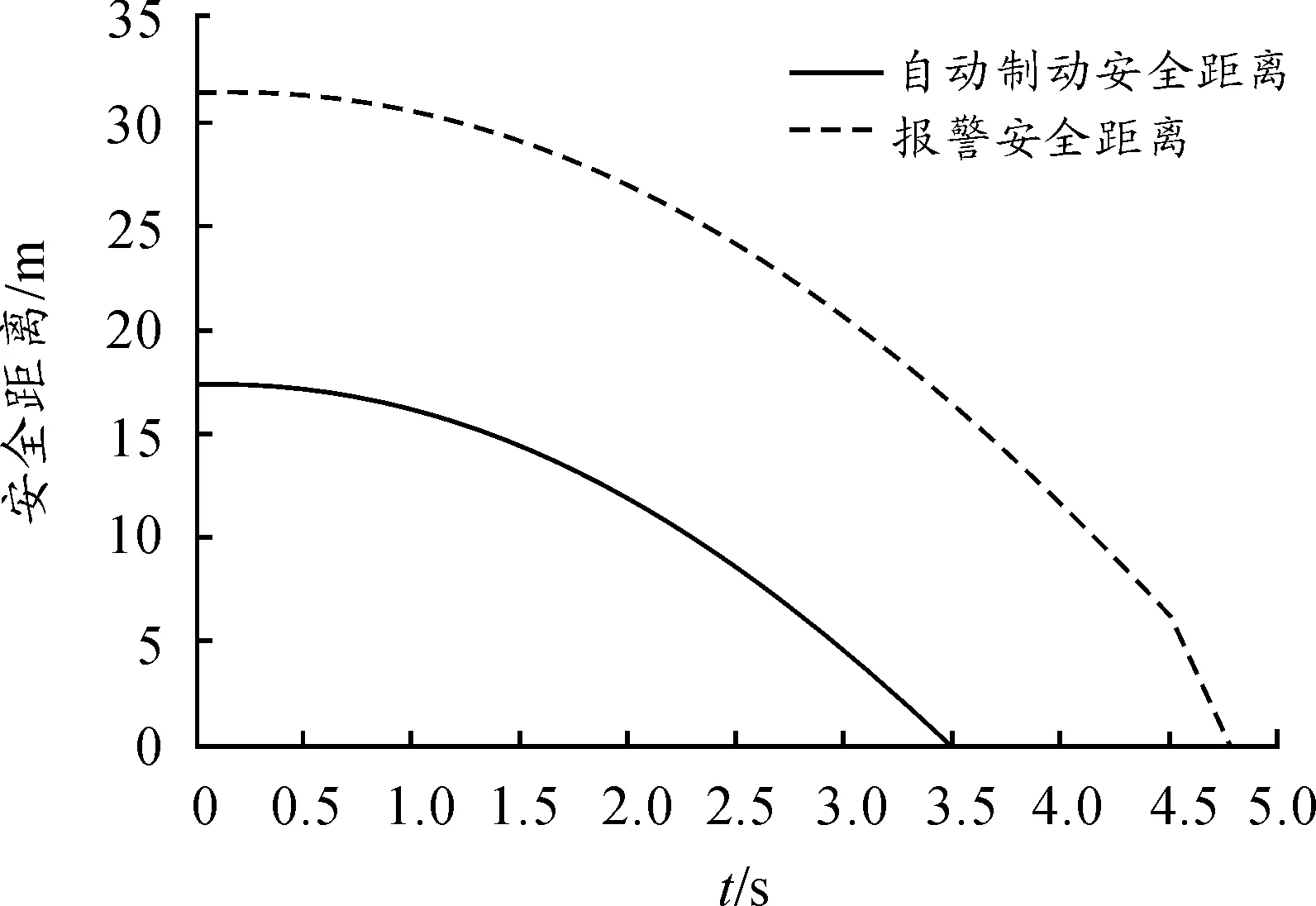
圖2　DRV安全距離模型報警安全距離與自動制動安全距離

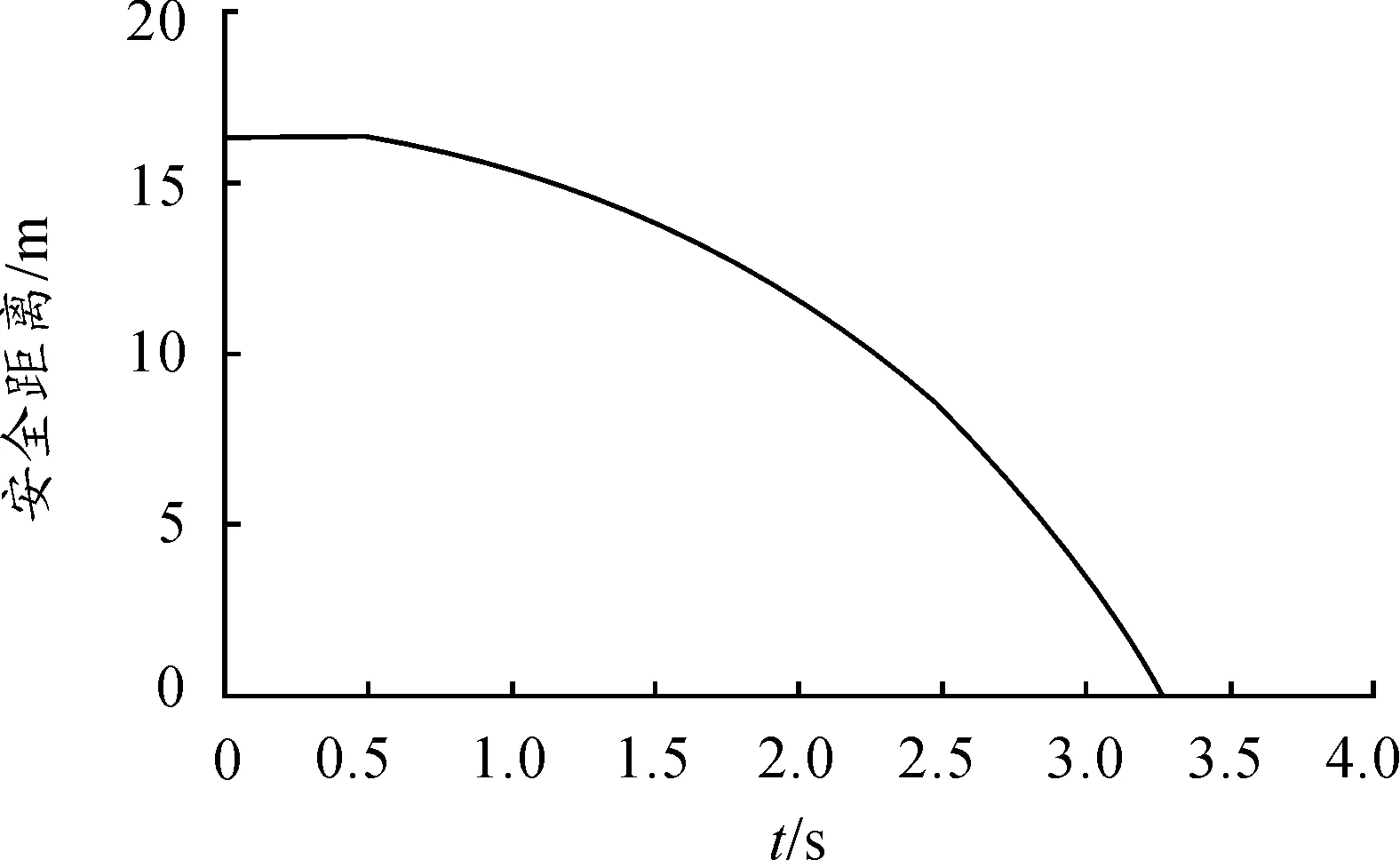
圖3　Hideo Araki模型的報警安全距離與自動制動安全距離

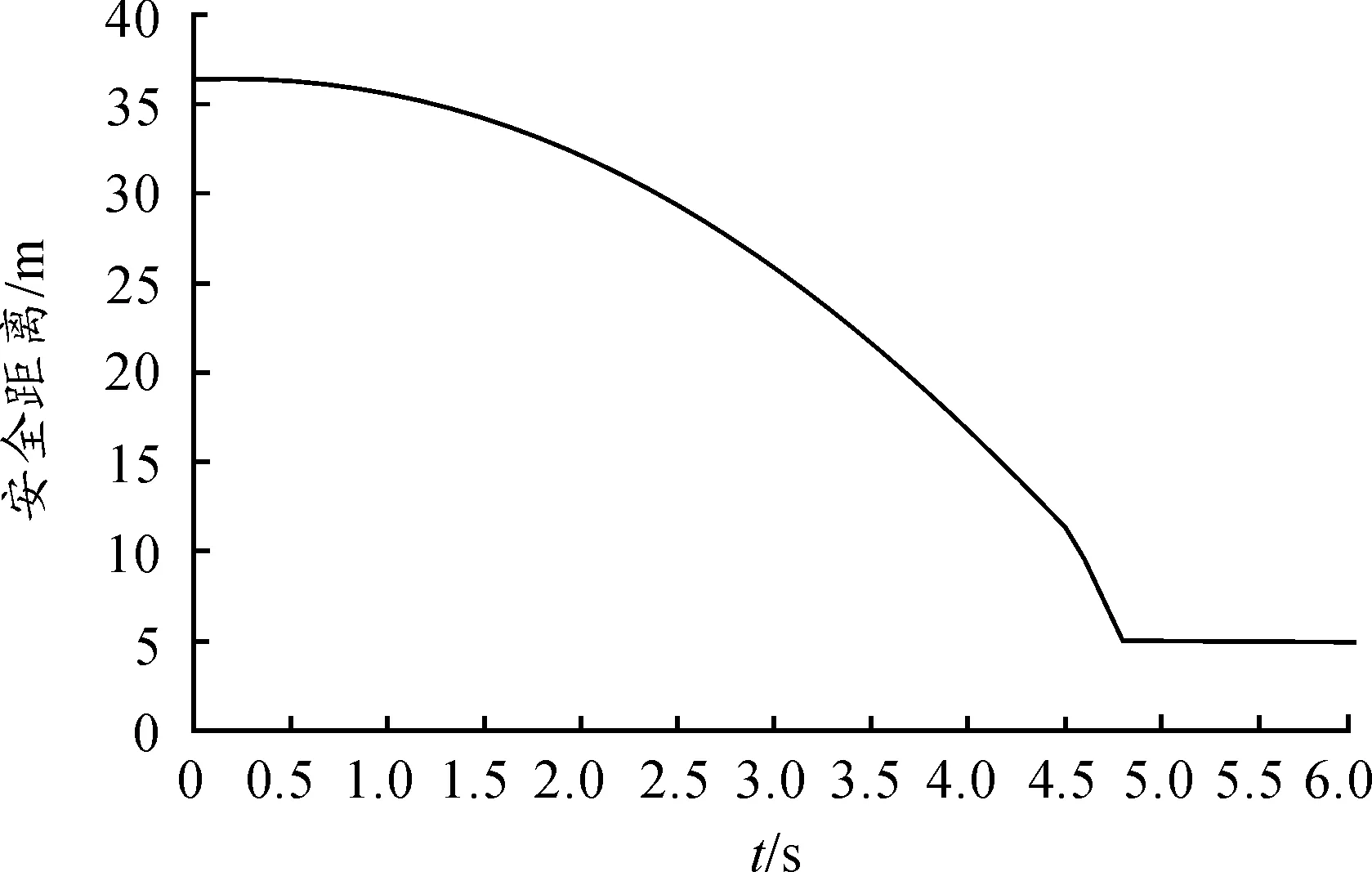
圖4　馬自達模型的報警安全距離

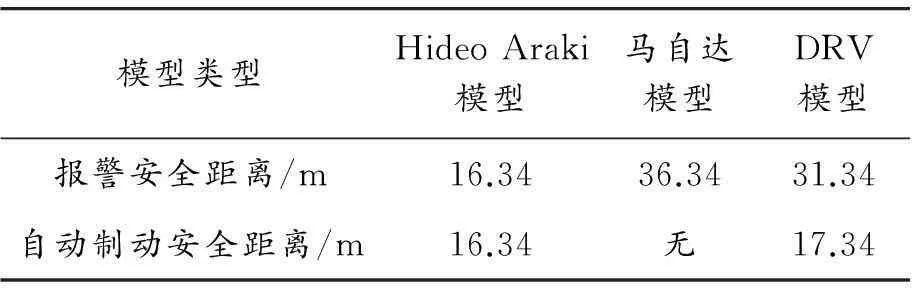
表3　3種安全距離對比結果

本文設計的DRV安全距離模型的仿真結果顯示報警安全距離為31.33 m，理論值為31.34 m，自動制動安全距離為17.33 m，理論值為17.34 m，誤差均在0.01 m左右。

綜上所述，由于Hideo Araki模型沒有考慮道路狀況、駕駛員狀態因素和車輛制動系統性能，因此所計算的報警安全距離嚴重偏小、自動制動安全距離偏小，最終會導致車輛追尾事故的發生。馬自達公司所采用的模型雖然沒有考慮道路坡度給安全距離模型帶來的影響，但有一個5 m的安全距離，在車輛下坡制動時能保證模型的有效性，但在上坡避撞狀態下會造成距離上的保守。

4結束語

在分析現有車輛安全距離模型的特點及不足的基礎上，綜合考慮駕駛員因素(driver factor )、交通路況因素(road factor)和車輛制動性能因素(vehicle factor)，建立了DRV安全距離模型。在同等條件下，對現有模型和DRV模型進行安全距離對比分析。結果表明：所建立的DRV安全距離模型可以兼顧駕駛員駕駛特點、交通路況因素和車輛制動性能因素，得到的報警安全距離和自動制動安全距離相比現有的模型更加合理。

參考文獻：

[1]NTTSA.Traffic Safety Facts 2010 Annual Report[R].USA:DOTHS,2011.

[2]李曉霞,李百川,侯德藻,等.車追尾碰撞預警系統開發研究[J].中國公路學報,2001,14(3):93-95.

[3]KYONGSU Y,MINSU W,SUNG H K,et al.An Experimental Investigation of a CW/CA System for Automobile Using Hardware in the Loop Simulation[C]// Proceedings of the American Control Conference.San Diego:[s.n.],1999.[4]SEILER P,SONG B,HEDRICK J.Development of a Collision Avoidance System[J].SAE,1998(10):9808535.[5]侯德藻,劉剛,高鋒,等.新型汽車主動避撞安全距離模型[J].汽車工程，2005(2):186-190.

[6]邊明遠.考慮駕駛員個體特性的汽車安全行駛間距模型[J].中國機械工程學報，2010，21(12)：1502-1506.

[7]董紅召,陳煒烽,陳寧,等.車路集成環境下車輛防撞預警安全狀態判別模型的研究[J].汽車工程,2011(9):1120-1123.

[8]GENYA A,JOHN R.Alarm Timing,Trust and Driver Expectation for Forward Collision Warning Systems[J].Applied Ergonomics,2006,37:577-586.

[9]LUIS A,JINGANG Y,BOBERTO H，et al.Emergency braking control in automated highway systems with underestimation of friction coefficient[C]//Proceedings of the American Control Conference.Chicago:[s.n.],2000:574-579.

[10]KENUE S K.Selection of range and azimuth angle parameters for a forward looking collision warning radar sensor[C]//Intelligent Transportation Systems’97.Boston:IEEE,1997:494-499.

[11]黨宏社，韓崇昭，段戰勝.汽車防碰撞報警與制動距離的確定[J].長安大學學報(自然科學版)，2002，22(6)：89-91.

[12]李霖，朱西產，馬志雄.駕駛員在真實交通危險工況中的制動反應時間[J].汽車工程，2014,36(10):1225-1229.

(責任編輯劉舸)

Vehicle Longitudinal Active Collision Avoidance DRVSafety Distance Model

YUAN Chao-chun, LI Dao-yu, WU Fei, LIU Yi-qun, ZHANG Long-fei

(School of Automotive and Traffic Engineering, Jiangsu University，Zhenjiang 212013，China)

Abstract:The effects of driver factors, road factors and vehicle, factors on the accuracy of the safety distance were analyzed and the DRV safety distance model was established innovatively. The effect of DRV safety distance model was tested by Prescan simulation platform. The results show that DRV safety distance model can consider driving safety and road usage simultaneously. The alarm safety distance and automatic breaking safety distance based on the DRV safety distance model are more reasonable.

Key words:vehicle engineering; collision avoidance; safety distance; Prescan simulation platform

收稿日期：2015-03-09

基金項目：國家自然科學基金資助項目(51305167)

作者簡介：袁朝春(1978—)，男，江蘇徐州人，博士，副教授，主要從事車輛主動安全、車輛底盤控制與系統設計、車輛整車動力學分析研究。

doi:10.3969/j.issn.1674-8425(z).2016.05.003

中圖分類號：U461.91

文獻標識碼：A

文章編號：1674-8425(2016)05-0015-05

引用格式：袁朝春，李道宇，吳飛，等.汽車縱向主動避撞DRV安全距離模型[J].重慶理工大學學報(自然科學)，2016(5):15-19.

Citation format：YUAN Chao-chun, LI Dao-yu, WU Fei, et al.Vehicle Longitudinal Active Collision Avoidance DRV Safety Distance Model[J].Journal of Chongqing University of Technology(Natural Science)，2016(5):15-19.