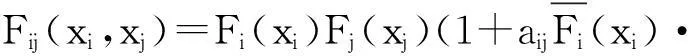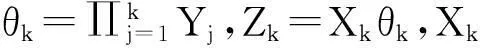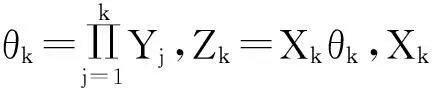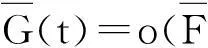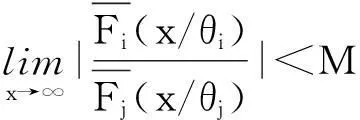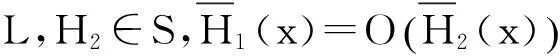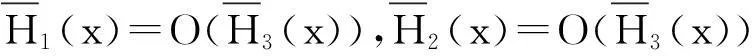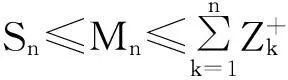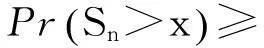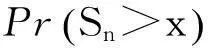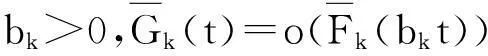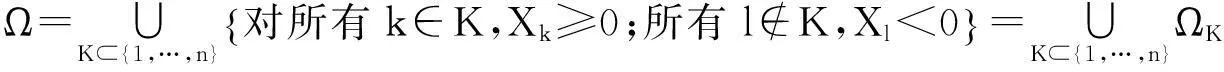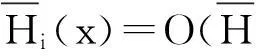保險和金融風險相依的破產概率研究

郭曉莉，文麗壹

(重慶理工大學 數學與統計學院，重慶　400054)

?

保險和金融風險相依的破產概率研究

郭曉莉，文麗壹

(重慶理工大學 數學與統計學院，重慶400054)

摘要：考慮一家保險公司暴露于保險風險和金融風險兩種風險環境，分別用兩組隨機變量量化這兩種風險，用離散時間風險模型表述保險公司盈余過程，研究了在保險風險和金融風險漸近獨立相依假設下的保險公司有限時間破產概率問題。當保險風險的分布屬于次指數分布族或長尾分布族時，分別推導了有限時間破產概率的漸近等價關系式，這將簡化保險公司在風險評估中的計算問題。

關鍵詞：保險風險；金融風險；破產概率；次指數；長尾

考慮一個離散時間保險風險模型。設保險公司的初始資本金為x≥0，保險公司第k年內的凈收入由實值隨機變量Ak(k=1,2,…,n)表示，保險公司在第k年將資金投入到有風險和無風險市場所產生的綜合收益率由非負隨機變量Bk(k=1,2,…,n)表示。假設保險公司的凈收入Ak在第k年的年末計算，則保險公司在第k年末的盈余值Uk滿足以下遞歸等式：

(1)

由式(1)遞歸可以得到：

(2)

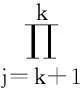
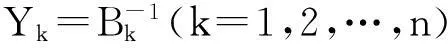
(3)

(4)

保險公司有限時間內的破產概率ψ(x;n)可重新表示為：

(5)

在實際應用中，直接計算保險公司在有限時間內的破產概率ψ(x;n)是相當繁瑣甚至不現實的，因此本文主要研究當x→∞時ψ(x;n)的漸近等價表達式。在現有文獻研究中，{Xk;k=1,2,…,n}和{Yk;k=1,2,…,n}分別被稱為保險風險和金融風險。離散時間保險風險模型的破產概率問題已經被廣泛研究。根據保險風險和金融風險相依關系分類，研究方向主要分以下3類：① {Xk;k=1,2,…,n}和{Yk;k=1,2,…,n}都是獨立隨機變量序列，且兩序列之間獨立，如文獻[1-4]；② {Xk;k=1,2,…,n}和{Yk;k=1,2,…,n}中至少有一組是相依的，但兩序列之間獨立，見文獻[5-7]；③ {Xk;k=1,2,…,n}和{Yk;k=1,2,…,n}兩序列之間存在相依關系，見文獻[8-11]。

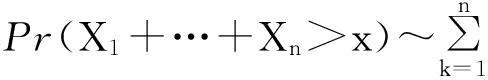
1預備知識和主要結論

本文除非另有說明，所有的極限關系都是在x→∞時成立。對于兩個正函數f(·)和g(·)，若limf(x)/g(x)=1，則記為 f(·)～g(·)；若liminff(x)/g(x)≥1，則記為 f(x)g(x)；若limsupf(x)/g(x)≤1，則記為f(x)g(x)。除此之外，定義x+=max{x,0}為實數x的正部。

1.1重尾分布族

這一部分給出重尾及兩類重尾分布族的定義，其余重尾分布族的介紹可參看文獻[12]。

定義1稱隨機變量X或者它的分布函數V是重尾的，如果對任意的s>0滿足

這里把重尾分布族記為K。

相反，稱隨機變量X或者它的分布函數V是輕尾的，如果存在一個s0>0，使得對所有0

定義2稱定義在R上的分布函數V屬于長尾分布族，若對任意的y≠0，滿足

記作V∈L。

定義3稱定義在R+上的分布函數V屬于次指數分布族，若對某任意的n≥2，滿足

記作V∈S。

在一般情況下，若定義在R上的分布函數V滿足V+(x)=V(x)I(x≥0)∈S，則也稱V∈S。

假設隨機變量X1,…,Xn獨立同分布，且分布函數V∈S，則有

顯然S?L，因為對任意定義在R+上的分布函數V∈S，x≥y>0，有

則當x→∞，V(x)-V(y)≠0時，

故V∈L。

1.2相依結構

考慮本文的離散時間保險風險模型，對k=1,2,…,n，實值隨機變量Xk滿足下面的相依結構：

顯然，假設A包含以下兩種情形：

常見的FGM相依也滿足漸近獨立條件。因為若隨機變量X1,…,Xn服從n維FGM分布：

1.3主要結論

(6)

(7)

2引理及證明

首先給出3個基本的引理，這3個引理在結果的證明中將會被用到。其中：引理1來自Cline[14]的推論2.5；引理2是文獻[2]中引理3.2的一個特例，即r=0的情形；引理3源自文獻[2]中引理3.10。針對所有引理，這里不再給出證明。

引理1如果隨機變量X的分布函數F∈S，隨機變量Y有界，則XY對應的分布函數H∈S。

因為Fk∈S，θk有界，則由引理1得Hk∈S。

H1*H2∈S且Pr(Z1+Z2>x)～Pr(Z1>x)+Pr(Z2>x)

H1*H2*H3∈S且Pr(Z1+Z2+Z3>x)～Pr(Z1>x)+Pr(Z2>x)+Pr(Z3>x)

以此類推，得H1*…*Hn∈S且Pr(Z1+…+Zn>x)～Pr(Z1>x)+…+Pr(Zn>x)，即

Pr(Zi>xi,Zj>xj)=o(1)Pr(Zj>xj)

因此：

又因為

故定理1得證。

根據文獻[6]引理4.1，由數學歸納法可得Sn的分布函數屬于L，即對某個A≠0，有

其中，M′是θl的上界。故定理2得證。

參考文獻:

[1]NYRHINEN H.On the ruin probabilities in a general economic environment[J].Stochastic Processes and their Applications,1999,83(2):319-330.

[2]TANG Q,TSITSIASHVILI G.Precise estimates for the ruin probability in finite horizon in a discrete-time model with heavy-tailed insurance and financial risks[J].Stochastic Processes and their Applications,2003,108(2):299-325.

[3]CHEN Y,XIE X.The finite time ruin probability with the same heavy-tailed insurance and financial risks[J].Acta Mathematicae Applicatae Sinica(English Series),2005,21(1):153-156.

[4]CHEN Y,SU C.Finite time ruin probability with heavy-tailed insurance and financial risks[J].Statistics & Probability Letters,2006,76(16):1812-1820.

[5]SHEN X,LIN Z,ZHANG Y.Uniform estimate for maximumof randomly weighted sums with applications to ruin theory[J].Methodology and Computing in Applied Probability,2009,11(4):669-685.

[6]CHEN Y,NG K W,YUEN K C.The maximum of randomly weighted sums with long tails in insurance and finance[J].Stochastic Analysis and Applications,2011,29(6):1033-1044.

[7]ZHOU M,WANG K,WANG Y.Estimates for the finite-time ruin probability with insurance and financial risks[J].Acta Mathematicae Applicatae Sinica(English Series),2012,28(4):795-806.

[8]GELUK J,TANG Q.Asymptotic Tail Probabilities of Sums of Dependent Subexponential Random Variables[J].Journal of Theoretical Probability,2009,22(4):871-882.

[9]CHEN,Y.The finite-time ruin probability with dependent insurance and financial risks[J].Journal of Applied Probability,2011,48(4):1035-1048.

[10]YANG Y,WANG K,LEIPUS R,et al.A note on the max-mum equivalence of randomly weighted sums of heavy-tailed random variables[J].Nonlinear Analysis:Modelling and Control,2013,18(4):519-525.

[11]CHEN Y,LIU J,LIU F.Ruin with insurance and financial risks following the least risky FGM dependence structure[J].Insurance: Mathematics and Economics,2015,62:98-106.

[12]EMBRECHTS P,KLUPPELBERG C,MIKOSCH T.Modelling Extremal Events for Insurance and Finance[M].Berlin:Springer-Verlag,1997.

[13]MAULIK K,RESNICK S.Characterizations and examples of hidden regular variation[J].Extremes,2004,7(1):31-67.

[14]CLINE D B H,SAMORODNITSKY G.Subexponentiality of the product of independent random variables[J].Stochastic Processes and their Applications,1994,49(1):75-98.

(責任編輯劉舸)

The Ruin Probability with Dependent Insurance and Financial Risks

GUO Xiao-li, WEN Li-yi

(Department of mathematics and statistics, Chongqing University of Technology,Chongqing 400054, China)

Abstract:Considering an insurance company exposed to an environment that contains insurance and financial risks, these two kinds of risks were quantified by two sets of random variables and the surplus process of the insurance company was described by a discrete-time risk model. This paper investigated the finite-time ruin probability with asymptotic independence insurance and financial risks. When the distributions of the insurance risk belong to the subexponential distribution class or the long-tailed distribution class, we derived some asymptotic equivalent relationships for the finite-time ruin probability, respectively. These will simplify the calculation of the insurance companies in the risk assessment.

Key words：insurance risk; financial risk; ruin probability; subexponentiality; long tail

收稿日期：2015-12-16

基金項目：國家社會科學基金資助項目(14BJY200)

作者簡介：郭曉莉(1991—)，女，河南周口人，碩士研究生，主要從事應用數學研究。

doi:10.3969/j.issn.1674-8425(z).2016.05.024

中圖分類號：O211.9

文獻標識碼：A

文章編號：1674-8425(2016)05-0135-06

引用格式：郭曉莉，文麗壹.保險和金融風險相依的破產概率研究[J].重慶理工大學學報(自然科學)，2016(5):135-140.

Citation format：GUO Xiao-li1, WEN Li-yi.The Ruin Probability with Dependent Insurance and Financial Risks[J].Journal of Chongqing University of Technology(Natural Science)，2016(5):135-140.