特殊發現：理解透徹打基礎

尹琳琳

課本的例題和習題中有不少問題可以通過增加、變換情境，改變設問方式，將一般性問題改為拓展遷移型問題. 該類型試題通過提供一段文字、素材或圖表材料，來展示一個數學要領、結論的形成和應用過程，或一個新數學公式的推導和應用，或介紹一種解題方法等. 近年來，此類題在中考試卷中頻頻出現，值得關注.

（2015·莆田）在Rt△ACB和Rt△AEF中，∠ACB=∠AEF=90°，若點P是BF的中點，連接PC，PE.

特殊發現：如圖1，若點E，F分別落在邊AB，AC上，則結論：PC=PE成立（不要求證明）.

問題探究：把圖1中的△AEF繞著點A順時針旋轉.

（1） 如圖2，若點E落在邊CA的延長線上，則上述結論是否成立？若成立，請給予證明；若不成立，請說明理由.

（2） 如圖3，若點F落在邊AB上，則上述結論是否仍然成立？若成立，請給予證明；若不成立，請說明理由.

（3） 記=k，當k為何值時，△CPE總是等邊三角形？（請直接寫出k的值，不必說明理由）

【思路突破】本題的“特殊發現”雖然不要求證明，但必須理解透徹. 這一步是利用直角三角形斜邊上的中線等于斜邊的一半這一定理. 這個問題中所涉及的證明思路和基本圖形將為下面問題的解決打下基礎.

問題探究（1） 通過作輔助線構造全等三角形，得對應邊相等，從而可以出現直角三角形斜邊上中線這一基本圖形，得到結論.

問題探究（2） 以問題探究（1）的解題思路為背景，同樣通過作輔助線得直角三角形，利用斜邊中線性質解題，只是解決這個問題時說明所構造的三角形是直角三角形是難點，需要利用兩步全等給予解決. 注意∠EAF=∠CAB是隱含條件.

問題探究（3） 從△CPE是等邊三角形入手，結合圓周角定理得到k的值.

解：（1） PC=PE成立，理由如下：

（2） PC=PE成立，理由如下：

（3） ∵△CPE是等邊三角形，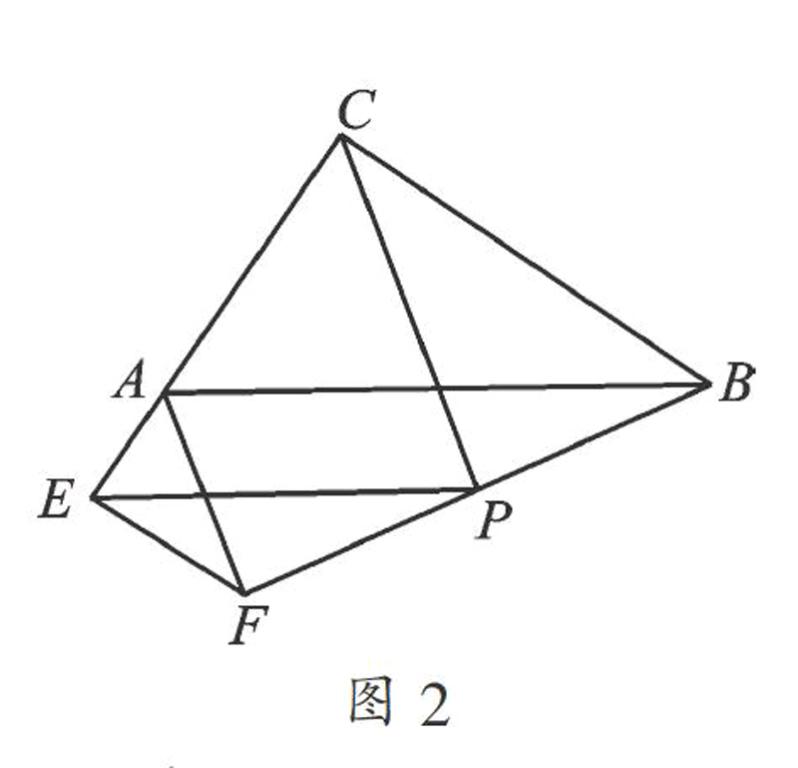

【解后反思】該試題設計的3個問題由淺入深，特殊發現給我們暗示了探究的方向和解題方法，問題（1）（2）是以特殊發現為基礎，在改變點E、F位置的過程中，圖形的形狀雖然發生了變化，但解決問題的方法不變，△CPB和△MPF的全等關系不變，即問題的本質不變. 想方設法尋找旋轉過程中的“變”與“不變”，其核心是找到“變”中的“不變”，解題的關鍵是抓住題目中的“題根”，聯想基本圖形，尋找解題的多種策略.