趣談數學中的黃金組合

孫翠微

同學，你是追星族嗎？你喜歡哪些音樂組合，TFboys或者EXO？在數學領域中也有一對黃金組合，他們是數學中的兩個最古老也是最基本的研究對象——數與形. 華羅庚先生曾指出：“數與形，本是相倚依，焉能分作兩邊飛. 數無形時少直覺，形少數時難入微. 數形結合百般好，隔離分家萬事休.” 這充分說明了數形結合在我們數學學習中的重要性. 當然啦，這對組合在解決很多中考數學問題時也會大放異彩，作用不可小覷！下面讓我們通過幾道中考題來領略一下“數形結合”的風采，體會它是如何把問題變抽象為直觀，化復雜為簡單的.

一、 以形助數

你在做題時是否有過這種感覺——明明題目給的數量信息很清楚，可就是難以把握，不知從何下手. 這是因為“數”比較抽象，不易尋找到各個條件之間的聯系，而“形”具有形象、直觀的優點，能表達較多具體的思維. 因此我們可以把“數”的對應——“形”找出來，利用圖形來解決問題，會有“四兩撥千斤”的神奇效果.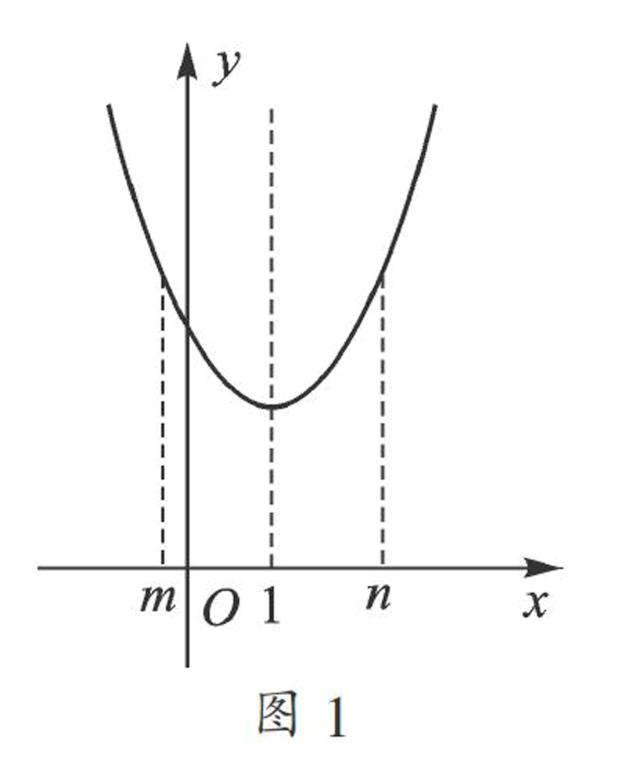

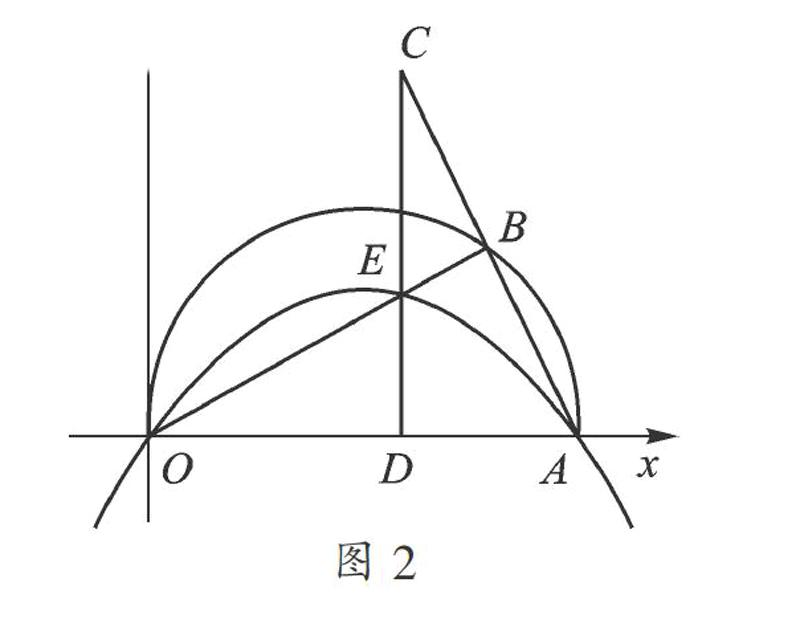
例1 （2015·宿遷）當x=m和x=n（m≠n）時，代數式x2-2x+3的值相等，則x=m+n時，代數式x2-2x+3的值為_______.

【分析】構造二次函數y=x2-2x+3，“見數思形”，該拋物線的對稱軸為直線x=1，由二次函數圖像的軸對稱性，結合當x=m和x=n時，y的值相等，可知拋物線的對稱軸為直線x=. 故有=1，如圖1，假設m

解：（思路一）m+n=2，當x=m+n時，即當x=2時，x2-2x+3=3.

（思路二）觀察圖像，因為其對稱軸為直線x=1=，所以當x=0時與當x=m+n時函數值應相等.易知當x=0時，y=x2-2x+3=3，故當x=m+n時，y=3.

變式 （2015·南通模擬）已知當x=a和x=a+b（b>0）時，代數式x2-2x-3的值相等，則當x=6a+3b-2時，代數式x2-2x+3的值等于_______.

二、 以數解形

“形”盡管直觀、形象，但在定量方面，卻離不開“數”的鼎力相助. 尤其是在較復雜的“形”中，可以嘗試把圖形數字化，搜尋隱含條件，合理利用圖形的性質或幾何意義，把“形”正確表示成“數”的形式，進行分析計算.

例2 （2015·徐州，有刪改）如圖2，在平面直角坐標系中，點A（10，0），以OA為直徑在第一象限內作半圓，B為半圓上一點，連接AB并延長至C，使BC=AB，過C作CD⊥x軸于點D，交線段OB于點E，已知CD=8，拋物線經過O、E、A三點.

（1） 求拋物線的函數表達式.

【分析】易得OB是AC的垂直平分線，連接OC，則OC=OA=10，利用勾股定理，得OD=6，C（6，8），B（8，4），求出OB所在直線的函數關系式從而得出點E的坐標，用待定系數法得拋物線的解析式.

解：（方法一）連接OC，作BG⊥x軸，如圖3所示.

易得OB是AC的垂直平分線，

∴OC=OA=10，

在Rt△OCD中，OC=10，CD=8，

∴OD=6，

又由△ABG∽△ACD，得AG=2，BG=4，

∴C（6，8），B（8，4），

∴OB所在直線的函數關系為y=x，

又∵E點的橫坐標為6，

∴E點縱坐標為3，

即E（6，3），

拋物線過O（0，0），E（6，3），A（10，0），

∴此拋物線的函數關系式為

y=-x2+x.

（方法二）∵CD⊥x軸，OB⊥AC，

∴∠DCA=∠BOA，

∴tan∠DCA=tan∠BOA，

即=，

∵OD=6，∴AD=4，

又∵CD=8，

∴ED=3，即E（6，3），

以下略.

【解后反思】第1小問的難點在于求出點E的坐標. 需要把OB所在直線理解為一次函數的圖像，以數解形，求出其函數關系式，進而尋找到突破口.

下面再看第2小問：

（2） 若P為拋物線上位于第一象限內的一個動點，以P、O、A、E為頂點的四邊形面積記作S，則S取何值時，相應的點P有且只有3個？

【分析】首先要認識到點P的位置可能在CD的左右兩側，其次要注意到點P在右側時該四邊形的最大面積比P在左側時該四邊形的最大面積要小，所以當點P在CD的右側某處四邊形面積取最大值時，在CD的左側有兩個點P滿足同樣的面積，此時相應的點P有且只有3個.

解：不妨設P的坐標為m，-m2+m，

①若點P在CD的左側，延長OP交CD于Q，如圖4，易得OP所在直線的函數關系式：

y=-m+x，

表示出Q點的縱坐標，

得QE的長，割補法表示出四邊形POAE的面積，

S四邊形POAE=S△OAE+S△OQE-S△PQE

=-m2+m+15，

②若點P在CD的右側，延長AP交CD于Q，如圖5，易得AP所在直線的關系式：

y=-mx+m，

從而求得Q點的縱坐標，得QE，求得四邊形AOPE的面積=S△OAE+S△AQE-S△PQE=

-m2+4m=-（m-8）2+16，

當P在CD右側時，四邊形POAE的面積最大值為16，此時點P的位置就一個.

令-m2+m+15=16，解得點P位置有兩個.

綜上所知，以P、O、A、E為頂點的四邊形面積S等于16時，相應的點P有且只有3個.

試試看，你能獨立把這道題完整地解下來嗎？坐標系背景下，解決幾何問題，是中考命題的熱點，寓形于數，數形結合，會讓問題解決起來輕松順暢.

怎么樣，“數形結合”是不是魅力無限？希望它會成為你的朋友，在解決數學問題時，一定會幫助你披荊斬棘，所向披靡.