透過表面看實質：新定義型問題

李帥領

“新定義”型問題是指在問題情境中定義一些沒有學過的新概念、新運算、新符號，需要大家結合已經學過的知識進行理解，根據新定義進行運算、推理、遷移的一種題型. 近年來中考數學中經常出現“新定義”型問題，同學們在復習中應該重視培養閱讀理解新知識并應用新知識解決問題的能力.

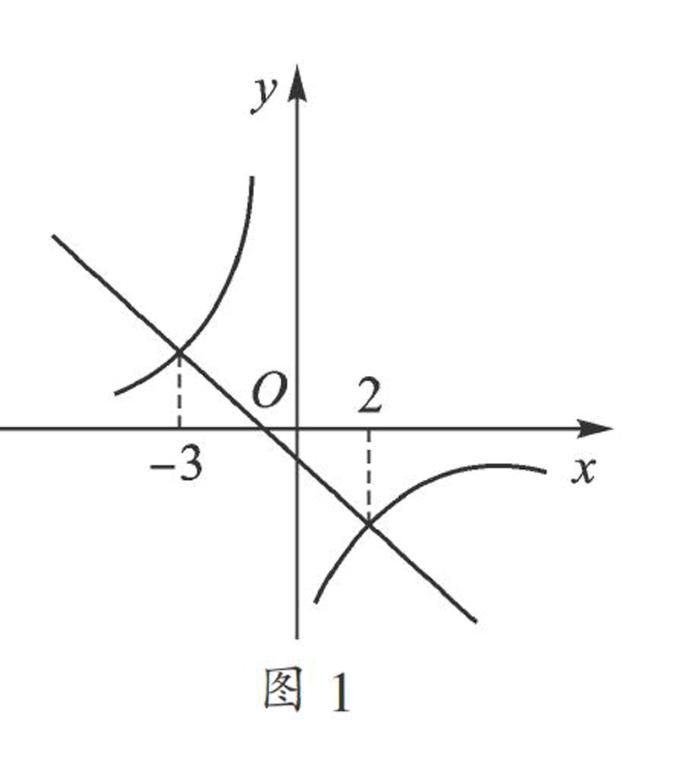
例1 （2015·慶陽）定義運算max{a，b}，當a≥b時，max{a，b}=a；當a

（1） max，3=_______；

（2） 已知y1=和y2=k2x+b在同一坐標系中的圖像如圖1所示，若max

，k2x+b=，結合圖像，直接寫出x的取值范圍；

（3） 用分類討論的方法，求max{2x+1，x-2}的值.

【思路突破】（1） 比較與3的大小；

（2） 根據題意可以得出≥k2x+b；

（3） 分2x+1≥x-2和2x+1

【解答】（1） max，3=3.

（2） x的取值范圍為-3≤x<0或x≥2.

（3） ①當2x+1≥x-2，即x≥-3時，max{2x+1，x-2}=2x+1；

②當2x+1

【解后反思】本題考查一次函數和反比例函數的交點問題的應用，分類討論思想等.

例2 （2015·永州）定義[x]為不超過x的最大整數，如[3.6]=3，[0.6]=0，[-3.6]=-4. 對于任意實數x，下列式子中錯誤的是（ ）.

A. [x]=x（x為整數）

B. 0≤x-[x]<1

C. [x+y]≤[x]+[y]

D. [n+x]=n+[x]（n為整數）

【思路突破】“定義[x]為不超過x的最大整數”可解釋為小于或等于x的最大整數.

【解答】當x是整數時，A成立；x為任意數時，B成立.

C不成立. 例如，[（-5.4）+（-3.2）]=[-8.6]=-9，[-5.4]+[-3.2]=-6+（-4）=-10，

∵-9>-10，

∴[-5.4-3.2]>[-5.4]+[-3.2].

D項也是成立的.

故選：C.

【解后反思】閱讀并理解[x]的含義：不超過即小于或等于是解決本題的關鍵.

例3 （2015·天水）定義運算：a？茚b=a（1-b）. 下面給出了關于這種運算的幾種結論：①2？茚（-2）=6，②a？茚b=b？茚a，③若a+b=0，則（a？茚a）+（b？茚b）=2ab，④若a？茚b=0，則a=0或b=1，其中結論正確的序號是（ ）.

A. ①④ B. ①③

C. ②③④ D. ①③④

【思路突破】根據題意得：

2？茚（-2）=2×[1-（-2）]=6，選項①正確；

a？茚b=a（1-b）=a-ab，b？茚a=b（1-a）=b-ab，不一定相等，選項②錯誤；

（a？茚a）+（b？茚b）=a（1-a）+b（1-b）=a+b-a2-b2=a+b-（a+b）2+2ab=2ab，選項③正確；

若a？茚b=a（1-b）=0，則a=0或b=1，選項④正確，故選D.

【解后反思】此題考查了整式的混合運算，以及有理數的混合運算，熟練掌握運算法則是解本題的關鍵.

例4 （2015·崇左）4個數a，b，c，d排列成a bc d，我們稱之為二階行列式. 規定它的運算法則為：a bc d=ad-bc. 若x+3 x-3x-3 x+3=12，則x=_______.

【思路突破】根據所給的二階行列式的概念，把行列式x+3 x-3x-3 x+3=12轉化為關于x的方程，算出方程的解得到答案.

解：行列式x+3 x-3x-3 x+3=12可以化為方程（x+3）2-（x-3）2=12，解得，x=1.

【解后反思】對于新定義的題，首先要看懂運算的法則，把新定義問題轉化為常規的數學問題來解決. 本題新定義的實質是將四個整式交叉相乘再求差化簡，最后轉化為解方程確定結果.

例5 （2015·臨沂）定義：給定關于x的函數y，對于該函數圖像上的任意兩點（x1，y1），（x2，y2），當x1

①y=2x；②y=-x+1；③y=x2（x>0）；④y=

-.

【思路突破】根據一次函數的性質，當k>0時，y隨x增大而增大；由二次函數的性質可知y=ax2的圖像過原點，當a>0時開口向上，對稱軸為y軸，當x>0時，y隨x的增大而增大；反比例函數的圖像是雙曲線，當k<0時，在每一個象限內，y隨x的增大而增大.應用這些性質便可輕易地解決問題.

【解答】y=2x，k>0，所以①是增函數.

y=-x+1，k=-1<0，所以②不是增函數.

y=x2，當x>0時，是增函數，所以③是增函數.

y=-，當x1=1時，y1=-1，當x2=-1時，y2=1，x1>x2，y1

【解后反思】本題考查的是一次函數、二次函數、反比例函數的性質，掌握各種函數的性質以及條件是解決問題的關鍵.