動態問題多變化，動靜結合巧分類

渠英

圖形運動問題是綜合性比較強的問題，也是中考的熱點，因此備受關注. 它需要以變化的、運動的觀點來處理問題，在解題中，要通過實驗、操作、觀察和想象的方法掌握運動的本質，在圖形的運動中找到不變量，然后解決問題. 下面結合2015年河北省壓軸題給出其解題思路，幫助同學們加深理解.

（2015·河北）平面上，矩形ABCD與直徑為QP的半圓K如圖1擺放，分別延長DA和QP交于點O，且∠DOQ=60°，OQ=OD=3，OP=2，OA=AB=1，讓線段OD及矩形ABCD位置固定，將線段OQ連帶著半圓K一起繞著點O按逆時針方向開始旋轉，設旋轉角為α（0°≤α≤60°）.

發現：

（1） 當α=0°，即初始位置時，點P_____直線AB上. （填“在”或“不在”）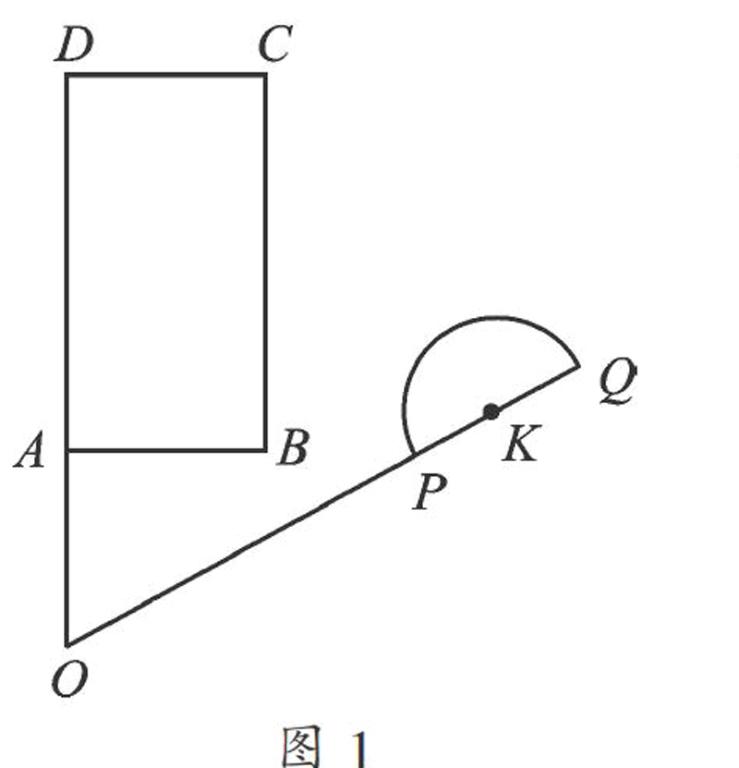

求當α是多少時，OQ經過點B.

（2） 在OQ旋轉過程中，簡要說明α是多少時，點P，A間的距離最小？并指出這個最小值.

（3） 如圖2，當點P恰好落在BC邊上時，求α及S陰影.

拓展：如圖3，當線段OQ與CB邊交于點M，與BA邊交于點N時，設BM=x（x>0），用含x的代數式表示BN的長，并求x的取值范圍.

探究：當半圓K與矩形ABCD的邊相切時，求sinα的值.

【思路突破】

發現（1）思路突破：

延長AB交直線OP于E，因為OA=1，∠O為60°，可求OE的長度等于2，即點E與點P重合，所以點P在直線AB上；當OQ經過點B時，如圖4，由△AOB是等腰直角三角形，可知∠AOB為45°，所以旋轉角α為15°.

發現（2）思路突破：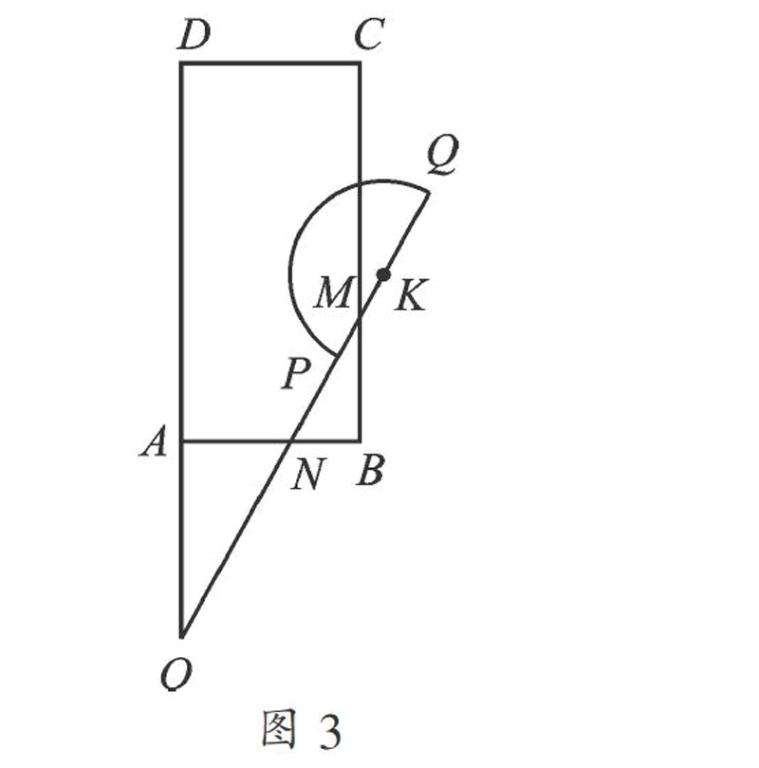

拓展思路突破：

如圖3，由∠ANO=∠BNM，則tan∠ANO=tan∠BNM，=，BN=.如圖6，因為OC>OD=OQ，所以當OQ轉到Q點在BC上時，BM即為x所取最大值.作QF⊥OD，在直角三角形FQO中，由勾股定理得：

探究思路突破：

【解后反思】

1. 關鍵步驟是哪幾步？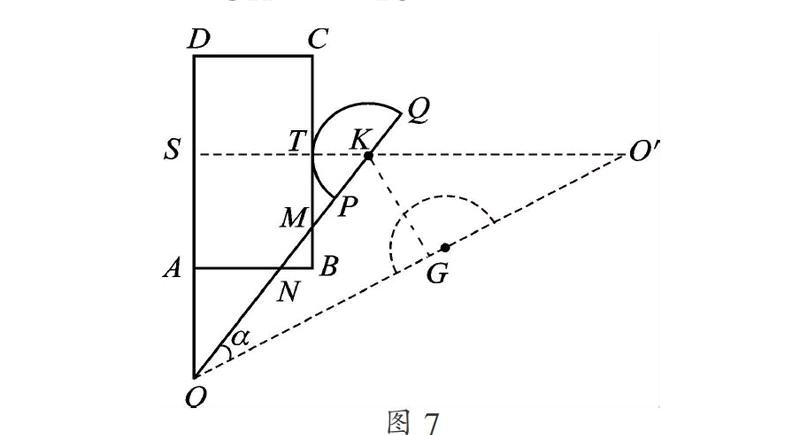

拓展的關鍵步驟是利用三角函數或三角形相似將BN用字母x表示，而求x的取值范圍時，只有OQ轉到Q點在BC上時，BM最大；另外，探究中的關鍵步驟是分類討論，半圓K與BC、AD相切容易想到，由于OQ=OD，半圓K與DC相切容易漏掉，構造直角三角形將∠α放在直角三角形中也是關鍵.

2. 有什么值得一學？

旋轉、三角函數、相似、直線與圓的位置關系、幾何中的最值、分類討論思想是本題涉及的知識，也是各地中考壓軸題的常見類型.在復習時，應注意問題的全面性、知識的連貫性及知識的遷移. 遇到直角三角形既可考慮相似又可考慮利用三角函數列方程，遇到運動問題要注意在利用分類討論解決問題時，做到不重不漏.