整合信息提高實效

李煥

隨著時代的發展進步，我們的生活越來越趨向信息化、數據化，與之相關的信息題也在中考數學中備受歡迎. 中考專家也為此加強了對圖表信息問題的關注，即通過對從實際生活中獲取的圖表信息進行觀察、整理、加工、處理，考查同學們分析問題，處理問題的能力. 解決此類問題的關鍵是要找準題眼，獲取信息，從而解決問題.

例1 某地區為了進一步緩解交通擁堵問題，決定修建一條長為6千米的公路. 平均每天的修建費y（萬元）與修建天數x（天）在30≤x≤120之間時具有一次函數的關系. 如下表所示：

（1） 求y關于x的函數關系式；

（2） 后來在修建的過程中計劃發生改變，政府決定多修2千米，因此在沒有增減建設力量的情況下，修完這條路比計劃晚了15天，求原計劃每天的修建費.

【思路突破】本題考查的是一次函數的應用.

（1） 通過仔細讀題、觀察表格可以設y與x之間的函數關系式為y=kx+b，運用待定系數法就可以求出y與x之間的函數關系式；

（2） 設原計劃要m天完成，因為計劃發生改變后，修完這條路比計劃晚了15天，則增加2 km后用了（m+15）天，根據每天修建的工作量不變建立方程求出其解，就可以得出計劃的時間，然后代入（1）的解析式即可求出答案.

解：（1） 設y與x之間的函數關系式為y=kx+b，將（50，40），（60，38）代入解析式得：

40=50k+b，38=60k+b.解得：k=-，b=50.

∴y與x之間的函數關系式為y=-x+50（30≤x≤120）.

（2） 設原計劃要m天完成，則增加2 km后用了（m+15）天，由題意，得=，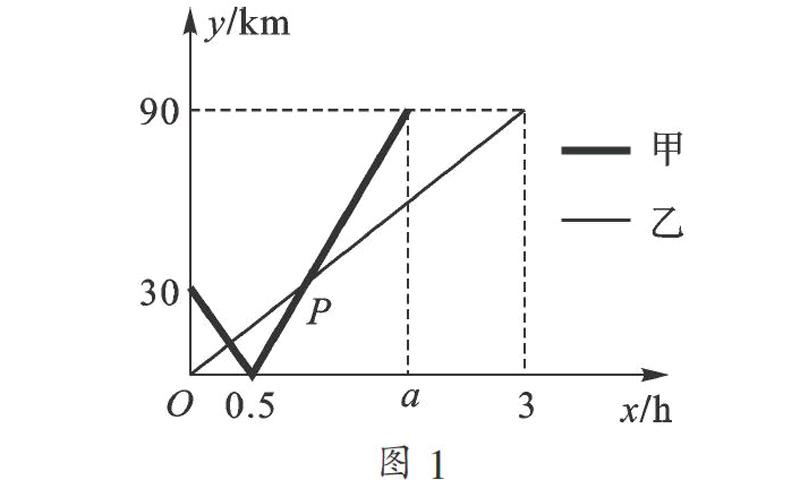

解得：m=45，經檢驗m=45是原方程的根.

所以原計劃每天的修建費為：-×45+50=41（萬元）.

【解后反思】本題考查了待定系數法求函數解析式的運用，也可以從圖像中讀取信息用方程解決.在列分式方程解實際問題時，可以設間接未知數來解答應用題，解答時建立分式方程求出計劃修建的時間是關鍵.

例2 在一條直線上依次有A，B，C三個港口，甲、乙兩船同時分別從A、B港口出發，沿直線勻速駛向C港，最終到達C港. 設甲、乙兩船行駛x（h）后，與B港的距離分別為y1、y2（km），y1、y2與x的函數關系如圖1所示.

（1） 填空：A，C兩港口間的距離為______km，a=______；

（2） 求圖中點P的坐標，并解釋該點坐標所表示的實際意義；

（3） 若兩船的距離不超過10 km時能夠相互望見，求甲、乙兩船可以相互望見時x的取值范圍.

【思路突破】本題考查數形結合思想及一次函數的應用.根據函數的圖像，我們可以把A，B，C三個港口的位置用線形示意圖畫出來，如圖2，圖像中點P表示當甲到達B港口后又經過了一段時間，甲、乙兩船與B港口的距離相等（或甲船追上乙船）.所以可以有兩種解法：一種是利用一次函數的解析式來求交點坐標；另一種則是利用追及問題的方法來解.若用第二種方法可設甲船追上乙船時，用了t小時，則可知甲船t小時比乙船多行了30 km，由圖1容易知道甲、乙兩船的速度分別是=60

【解后反思】本題考查了數形結合、分類討論的數學思想. 解題的關鍵是認真讀題、看懂圖，利用線形示意圖確定三個港口的位置. 難點在于第（3）問要分類討論.