基于最大Lyapunov指數的數控機床精度狀態識別方法

杜柳青，王立明，閆　哲，曾翠蘭

(重慶理工大學 機械工程學院，重慶　400054)

?

基于最大Lyapunov指數的數控機床精度狀態識別方法

杜柳青，王立明，閆哲，曾翠蘭

(重慶理工大學 機械工程學院，重慶400054)

摘要：提出一種基于最大Lyapunov指數的數控機床精度狀態識別方法。通過數控機床在XOY平面四種不同圓周進給速度下的圓度誤差數據產生一維時間序列，依據小波方法對時間序列降噪后采用C-C方法計算得到時間延遲、嵌入維數等混沌特性參數，對數控機床進行混沌相空間重構。求取Wolf方法下的最大Lyapunov指數，結合功率譜圖對比分析發現機床系統具有混沌特性，且隨著圓周進給速度的增加，最大Lyapunov指數減小；并通過實驗測試及分析驗證了這一結論。

關鍵詞：混沌；數控機床；精度狀態；Lyapunov指數

0引言

數控機床是機械制造行業的母機，其精度直接影響著加工工件的精度；機床本體存在的誤差會直接復映到加工形狀上，增大加工工件誤差。在高精度加工過程中為保證加工質量，對機床精度進行狀態識別就顯得尤為重要。

近年來，人們對數控機床精度狀態識別領域的研究主要偏向于數控機床誤差辨識[1-2]、精度檢測[3-4]等方面，卻增大了機床的故障停機時間，降低了數控裝備的服役可靠性[5-6]。文獻[7-8]分別用剛體動力學建立了三軸立式加工中心的運動誤差模型，研究發現運動精度隨空間坐標位置變化而變化，因此在數控加工程序的編制時，避開不利的空間區域是減緩數控機床的精度衰退的有效措施；文獻[9]綜合橋式加工中心樣機各項精度指標的測試結果，獲得機床的實際精度表現和分布規律，可以對樣機在各項精度指標上所反映出的精度問題進行評價；由以上文獻可以發現，機床精度狀態的影響因素多樣復雜，特定模型只適用于對應類型機床，不具有普遍性。

數控機床在工作過程中，系統內部各要素之間及與外部系統的相互作用具有明顯的非線性特征；利用最大Lyapunov指數研究非線性系統的混沌特性、判斷混沌狀態、進行系統混沌識別，為非線性動力系統的狀態識別提供了有效方法[10]。而在非線性狀態下對數控機床精度進行狀態識別的研究很少，因此本文提出了一種基于最大Lyapunov指數的數控機床精度狀態識別方法，通過數控機床在不同圓周進給速度下的圓度誤差測試獲取機床誤差時間序列，經過序列降噪、相空間重構等分析，深入討論基于最大Lyapunov指數對數控機床精度進行識別的可行性和準確性，為機床誤差混沌溯因提供了技術支持。

1機床精度時間序列預處理

混沌現象是非線性動態系統所特有的一種運動形式，在一定控制參數范圍內產生對初始條件具有敏感依賴性的非周期行為運動，表面上是無序的，在動力學上是確定的[11-12]。因此，數控機床運動精度狀態可視為一種具有混沌特征的復雜非線性狀態。

分析混沌時間序列，首先需要判別觀測系統的運動形式是否為混沌運動，然后借助于混沌序列的相空間，應用混沌分析方法，分析系統的運動規律。為對數控機床精度狀態進行識別，獲取數控機床的誤差演化量時間序列。本文以某型高速立式加工中心為實驗研究對象，使用Renishaw QC20球桿儀儀器測量機床XOY平面的運動誤差，使機床在半徑為100mm、進給速度分別為1000mm/min、3000mm/min、5000mm/min、7000mm/min條件下做圓周運動。

1.1時間序列獲取

將各采集點圓度誤差數據前后相減，得到機床圓度誤差演化的一維時間序列x(t)，t=0，1，2，…，N(N為采樣點數)，對時間序列x(t)進行相空間重構，得到一組新的向量序列X(t)={x(t)，x(t+τd)，x(t+2τd)，…，x[t+(m-1)τd]}T，(t=1，2，…，N-m+1),式中m為重構相空間的嵌入維數，τd為時間延遲。

1.2小波方法時間序列去噪

由于混沌系統對初始條件的敏感性、依賴性，很小的誤差就會影響系統的精度，因此需要對實際觀測的混沌時間序列進行去噪處理。小波變換分析可以對實際觀測信號進行有效的噪聲水平估計。以F=1000mm/min為例，實測圓度誤差時間序列如圖1所示。

圖1　1000mm/min 機床圓度誤差時間序列

圖2　1000mm/min 機床圓度誤差時間序列去噪

圖1中的信號既包含機床的圓度誤差信息，也包含了儀器測量精度引起的噪聲；借助小波變換在濾除信號觀測噪聲上的優異性[13]，對圖1信號進行去噪處理如圖2。小波變換對圖1信號進行多尺度細化分析，保證了很好的時頻局部化特點；將圖2與圖1比較可發現，圖2噪聲平滑后的誤差信號保留了圖1信號的一般特性，真實誤差信號的幅值基本保持不變，而噪聲信號的幅值迅速衰減，達到了較好的噪聲平滑效果。

1.3時間序列功率譜分析

以F=1000mm/min為例，對去噪后的時間序列求功率譜如圖3所示。

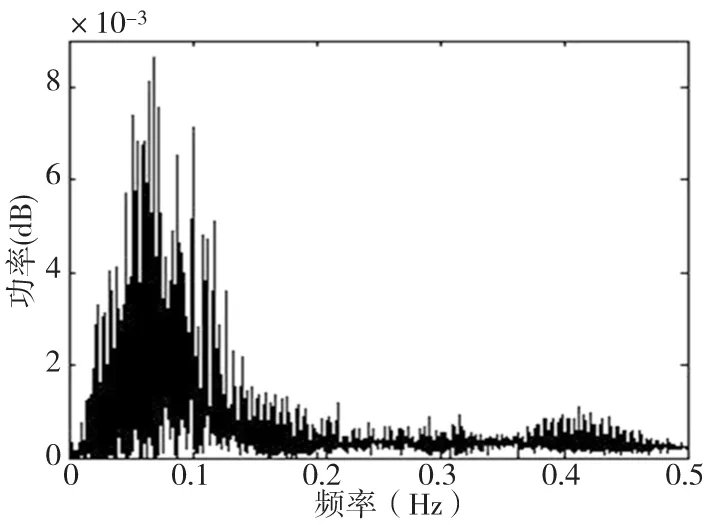
圖3　1000mm/min 功率譜圖

圖3表明，此信號功率譜呈現連續分布特征，并在低頻區有很大的振動幅度。因為混沌運動的復雜性，混沌信號的頻譜具有有限帶寬；并且混沌圓度誤差信號是多種非線性影響因素的綜合反映，所以在數控機床系統中這些非線性影響因素大都集中在低頻區[14]，這說明低頻區的振動信號中有較強的混沌成分。因此初步判定機床圓度誤差信號符合混沌信號特點。

2基于C-C方法的精度相空間重構

相空間重構是混沌時間序列分析的基礎，獲取的機床誤差時間序列是一維的，需要擴展到高位的相空間中以恢復系統所蘊含的信息。本文利用C-C方法同時計算時間延遲τd和嵌入維數m兩個參數。

將機床誤差時間序列分為t個不相交的子序列(t，即圖4的橫坐標)，然后定義每個子序列的統計量：

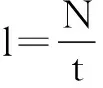
其中，m=2，3，…；計算過程中，取m=2，3，4，5；

所得曲線圖如圖4所示。

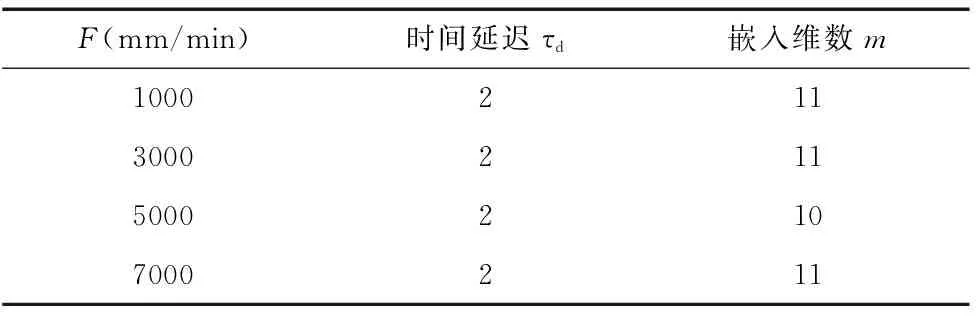
表1　不同F下的τd、m

由表1可看出，四種不同進給速度下，機床圓度誤差時間序列去噪后所得時間延遲τd與嵌入維數m基本保持不變。繼續觀察四種不同進給速度時最大Lyapunov指數的情況。

3基于Wolf方法的Lyapunov指數計算

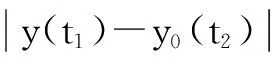
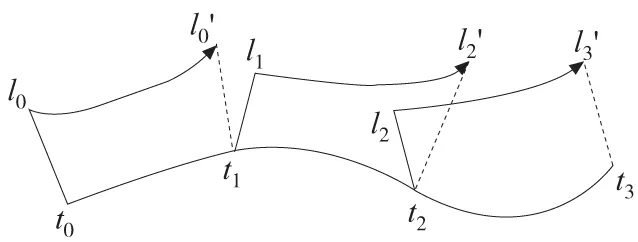
圖5　Wolf方法的示意圖

經過計算可得四種不同進給速度時的最大Lyapunov指數分別為0.0353、0.0237、0.0209、0.0060，如圖6所示。

圖6　不同F時的最大Lyapunov指數變化圖

由圖6可看出，四種不同機床圓周進給速度下的誤差時間序列所得最大Lyapunov指數均為正，表明機床系統具有混沌特性，且隨著圓周進給速度的增加，最大Lyapunov指數呈現逐漸減小趨勢，系統的混沌程度降低；鑒于本次球桿儀測量實驗結果顯示圓周F增大時的機床誤差呈增大趨勢，因此可得結論：對機床圓度誤差時間序列分析，機床精度越高，最大Lyapunov指數越大，混沌特性強；機床精度降低時，最大Lyapunov指數減小，混沌特性減弱。

為驗證這一方法的正確性，對該型機床XOZ、YOZ平面進行測試并計算求最大Lyapunov指數，如圖7所示。

并通過對5種不同型號數控機床XOY平面做同樣的測試分析實驗，提取圓度誤差數據，計算求最大Lyapunov指數得到結果如圖8。

圖7　XOZ、YOZ平面最大Lyapunov指數

圖8　各機床XOY平面最大Lyapunov指數

圖7、圖8數據均表明，最大Lyapunov指數隨著圓周進給速度的增加而減小，驗證了本文XOY平面圓度誤差時間序列分析所得結論的正確性。

4結論

基于機床圓度誤差時間序列，通過優選時間延遲和嵌入維數求得XOY平面最大Lyapunov指數，結果指數?>0表明機床系統具有混沌特性。通過對不同圓周進給速度及不同型號的機床系統進一步分析發現，機床精度越高，最大Lyapunov指數越大，混沌特性強；機床精度降低時，最大Lyapunov指數減小，混沌特性減弱。經過驗證證明這一結論的可信度是較高的，能為數控機床精度狀態識別研究提供新思路，并為機床精度混沌溯因提供理論支撐。

[參考文獻]

[1] Mann S，Bedi S，Israeli G，et al．Machine models and tool motions for simulating five-axis machining[J]. Computer Aided Design，2010，42(3)：23l-237.

[2] 薩日娜，張樹有，劉曉健. 面向零件切削性評價的數控機床精度特性重要度耦合識別技術[J].機械工程學報，2013，49(9)：113-120.

[3] 樊澤明,黃玉美,程祥,等. 加工工件位置和姿態的自動檢測、識別與校正方法(英文)[J]. 儀器儀表學報，2005,26(2):111-115,123.

[4] 黃克,關立文,王立平. 五軸數控機床精度建模與預測研究[J]. 組合機床與自動化加工技術，2015(2):78-81.

[5] 孫志禮,張義民.數控機床性能分析及可靠性設計技術[M].北京:機械工業出版社, 2011.

[6] 郝慶波. 數控機床可靠性及維修性的模糊綜合分配與預計[D] .長春:吉林大學，2012.

[7] Zhu W D, Wang Z G, YAMAZAKI K. Machine Tool Component Error Extraction and Error Compensation by Incorporating Statistical Analysis [J]. International Journal of Machine Tools& Manufacture，2010，40:1199-1213.

[8] Lee D M, Yang S H. Mathematical Approach and General Formulation for Error Synthesis Modeling of Multi-axis System [J]. International Journal of Modern Physics， 2010，16:1535-1546.

[9] 仇健. GMC2550u橋式加工中心樣機綜合精度測評研究[J]. 機械工程學報，2014,50(1):137-151.

[10] 肖達川,何青. 非線性系統中軌線的最小李雅普諾夫指數的計算[J]. 清華大學學報(自然科學版),1994,34(6):100-102.

[11] 史麗晨. 基于故障機理分析的往復式活塞隔膜泵狀態監測與故障診斷技術的研究[D].西安:西安建筑科技大學，2009.

[12] 肖勇,戴躍洪,張睿,等. 不確定微機電混沌系統的反演自適應控制[J]. 組合機床與自動化加工技術，2014(7):106-108.

[13] Han M, Liu Y H, Xi J H, et al. A Systematic Chaotic Noise Reduction Method Combining with Neural Network [J]. Proceedings of the Second International Symposium on Neural Network, China, 2005, 3497:580-585.

[14] 呂金虎.混沌時間序列分析及其應用 [M].武漢:武漢大學出版社，2005.

(編輯趙蓉)

Method for Recognition of CNC Machine Tool Precision State Based on the Largest Lyapunov Exponent

DU Liu-qing，WANG Li-ming，YAN Zhe，ZENG Cui-lan

(College of mechanical engineering, Chongqing University of Technology, Chongqing 400054, China)

Abstract：The method for recognition of CNC machine tool precision state was proposed based on the largest lyapunov exponent. One-dimensional time series is generated by the roundness error data in the XOY plane of four kinds of different circular feed rate. The wavelet analysis is adopted to denoise the time series. The chaotic characteristic parameters, such as time delay, embedding dimension, are obtained based on the C-C method, and then the chaotic phase space of CNC machine tool is reconstructed. The Wolf method is used to calculate the largest Lyapunov exponent, and with the power spectrum picture, the chaotic characteristic of the machine tool system is found. With the increase of circular feed rate, the largest Lyapunov exponent decreases. This conclusion is verified by experiment test and analysis.

Key words：chaos; CNC machine tool; precision state; Lyapunov exponent

文章編號：1001-2265(2016)05-0096-04

DOI:10.13462/j.cnki.mmtamt.2016.05.026

收稿日期：2015-09-25；修回日期：2015-11-13

*基金項目：國家自然科學基金項目"基于混沌相空間重構的數控機床精度非線性動力學演化、預測與溯因新方法"(51305476)

作者簡介：杜柳青(1975—)，女，重慶長壽人，重慶理工大學教授，碩士生導師，研究方向為機床精度設計，(E-mail)lqdu1@126.com。

中圖分類號：TH166;TG506

文獻標識碼：A