永磁直線同步電機的自適應濾波迭代學習控制*

趙希梅，馬志軍，朱國昕

(沈陽工業大學 電氣工程學院，沈陽　110870)

?

永磁直線同步電機的自適應濾波迭代學習控制*

趙希梅，馬志軍，朱國昕

(沈陽工業大學 電氣工程學院，沈陽110870)

摘要：針對永磁直線同步電機(PMLSM)迭代學習控制(ILC)過程中非重復性擾動放大的問題，提出一種自適應濾波ILC方案。該控制方案由一個直接反饋環和一個附加的ILC回路組成。在ILC回路上設計開環PD型學習律，與反饋控制器相結合使伺服系統快速收斂，并保證系統具有較高的控制精度。依據偽Wigner-Ville分布獲得的信號時頻分布信息，設計帶寬沿時間軸變化的自適應濾波器Q，避免了在迭代學習過程中非重復性擾動的放大。實驗結果表明，所提出的控制方案在提高位置跟蹤精度的同時，有效地增強了系統的魯棒性。

關鍵詞：永磁直線同步電機；迭代學習控制；自適應濾波器；魯棒性；跟蹤精度

0引言

PMLSM與傳統“旋轉電機+滾珠絲杠”的驅動方式相比，采用了直接驅動方式，中間不需要任何的轉換環節，具有推力大、損耗低、響應速度快、電氣時間常數小等優點，被廣泛應用于高速與高精度數控、精密儀器、電子制造裝備等領域[1-2]。電機運行時，摩擦力、端部效應等重復性擾動和參數攝動、測量波動等非重復性擾動毫無衰減地反映到電機動子及控制器上，增加了伺服控制難度，因此提高了對控制器設計的要求[3-4]。

對于重復運行的伺服系統，ILC理論上可以獲得完全跟蹤，但系統存在非重復性擾動時，在迭代軸上會無限放大擾動，在這種情況下，系統的魯棒性成為迭代ILC中的一個難題[5]。文獻[6]設計一種基于自適應ILC的PMLSM伺服系統，加快了收斂速度，但沒考慮系統中的非重復性擾動。文獻[7]利用P型ILC對PMLSM伺服系統進行位置誤差補償，由于濾波器設計簡單，很難有效地抑制測量噪聲。文獻[8]在ILC中加入自適應濾波器Q抑制噪聲，但學習濾波器的設計嚴重依賴系統模型，當系統參數變化或建模存在誤差時控制效果不佳。

針對上述問題，本文提出一種自適應濾波ILC方案。控制系統由反饋環和ILC回路組成，ILC與反饋控制器相結合保證了系統的跟蹤精度，自適應濾波器Q限制了擾動的放大、提高了系統的魯棒性。最后通過實驗表明了所提出的控制方案是有效可行的。

1PMLSM數學模型

在磁場定向矢量控制條件下(id=0)，對PMLSM進行矢量控制，則PMLSM電磁推力方程為：

(1)

PMLSM機械運動方程為：

(2)

(3)

Fripple=fslot+fend=A1sin(2πy/τ)+A2cos(2πy/τ+θ)

(4)

其中，Fripple為推力脈動，fslot為齒槽力，fend為端部效應，A1為齒槽力波動的幅值，A2為端部效應力波動的幅值，θ為初始相位電角度。

2伺服系統設計

2.1PMLSM自適應濾波迭代學習控制系統

PMLSM自適應濾波迭代學習控制系統框圖如圖1所示。ILC為迭代學習控制器，L與vk構成PD學習律，Q為自適應低通濾波器。P為被控對象PMLSM，yd為期望位置，yk+1為第k+1次迭代的輸出位置，ek+1為第k+1次迭代的位置誤差，uk+1為第k+1次迭代的控制信號，lk+1為被時域分析的信號，ηk+1為第k+1次迭代的測量擾動。C為PD反饋控制器，保證系統的穩定性、提高控制精度。

圖1　PMLSM自適應濾波迭代學習控制系統框圖

由圖1可以看出：

uk+1=Cek+1+vk+1

(5)

vk+1=Q(vk+Lek)

(6)

則ILC收斂的充分條件為[9]：

(7)

其中,P1=PS，并且靈敏度函數S1/(1+CP)。P型ILC的收斂速度快，但控制精度不高，D型ILC可達到較高的控制精度，但收斂速度比較慢[10]。因此本文采用開環PD型學習律，設計如下：

(8)

當系數K1和K2確定后，L實際上為一個PD控制器[11]。若選擇適當的參數K1、K2使L滿足式(7)則系統收斂。

2.2時頻分析

設計自適應濾波器Q之前需要利用偽Wigner-Ville分布對信號時頻分析，它有很高的時頻分辨率，并且減少了Wigner-Ville分布的交叉項，偽Wigner-Ville分布的定義為：

(9)

其中t，ω∈R，s*是所分析的時間信號s的復共軛，ω是單位為赫茲的頻率，h(τ)是實的偶窗函數，并且h(0)=0。

為了模仿直線電機啟動與停止時的推力狀態，選擇圖2中的曲線作為PMLSM的期望位置和加速度。圖3為對圖2中的期望位置跟蹤時系統運行1次后誤差的偽Wigner-Ville分布圖，可以看出有用的高頻誤差信號主要集中在零點附近和加速度變化的時間段，因此該時間段濾波器Q的帶寬應較大，以利用更多有用的信息，其它時間段濾波器Q的帶寬應較小，過濾更多噪聲。

圖2　PMLSM的期望位置和加速度曲線

圖3　PMLSM運行1次后誤差信號的偽Wigner-Ville分布

2.3自適應濾波器Q設計

迭代5次后觀察信號lk+1的偽Wigner-Ville分布的三維圖可發現高頻時間段噪聲的能量被放大，把Ce作為低頻可用信號與噪聲信號的分界點，則迭代k次時，能量超過Ce的頻率包絡Fmax(t)為：

(10)

其中W()是第k次迭代時信號lk的偽Wigner-Ville分布，把Fmax(t)作為帶寬Ω(t)自適應更新律的增益，用δNk(t)評估自適應濾波器帶寬變化對誤差帶來的影響，即：

δNk(t)=Nk(t)-Nk-1(t)

(11)

其中：

(12)

T為時間寬，設計帶寬Ω(t)的更新律為:

Ωk+1(t)=Ωk(t)+δΩk(t)

(13)

δΩk(t)=Fmax,k(t)·K·Kk(t)

(14)

其中：

Kk(t)=δNk(t)·(-sgn(δΩk-1(t)))

(15)

初始帶寬Ω0要盡可能小，為了避免因帶寬變化太快引起的控制性能下降，帶寬使用前使用中值濾波器對其進行平滑處理。

3實驗與分析

基于DSP的PMLSM控制系統原理框圖如圖4所示，本實驗采用TMS320LF2407A DSP為核心控制單元，驅動電路采用IPM，動子電流檢測單元采用霍爾傳感器，位置、速度檢測采用直線光柵尺。PMLSM采用派克公司的110-2，參數為：R=1Ω，L=8.5 mH，M=0.66 kg，B=0.2 N·s/m，τ=60.96 mm，p=4，Ψf=0.16 Wb。

圖4　基于DSP的PMLSM控制系統原理框圖

PD型ILC和自適應濾波ILC對圖2中的期望位置跟蹤，兩者的反饋控制器C相同，參數為Kp=12000、Kd=110。PD型ILC學習律的參數選擇為K1=1750、K2=0.03。由于電機重復誤差信號集中在20Hz以下，自適應濾波ILC中Q的參數選擇為Ω0=20Hz、K=1×1013、T=0.008，由于Q可以抑制擾動，學習律的參數K1可以選擇為較大值，即K1=2550、K2=0.03。PD型ILC迭代15次后的位置誤差曲線如圖5所示，最大誤差為18.9μm。圖6為自適應濾波ILC迭代15次后的位置誤差曲線，由于摩擦力等的影響，可看出初始位置誤差較大，為7.8μm，零時刻以后的最大誤差為6.5μm。經對比可知，自適應濾波ILC零時刻以后的最大位置誤差減小了約2/3。圖7為迭代15次后Q的最終帶寬,可看到帶寬的變化達到了預期的效果。

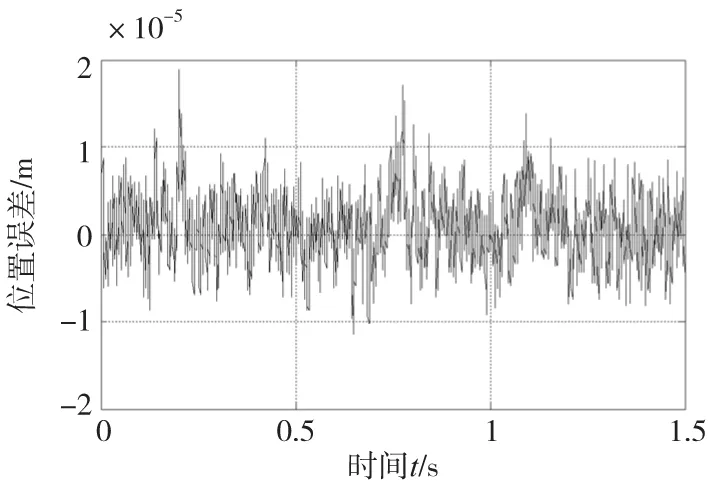
圖5　基于PD型ILC的PMLSM位置跟蹤誤差曲線

圖6　基于自適應濾波ILC的PMLSM位置跟蹤誤差曲線

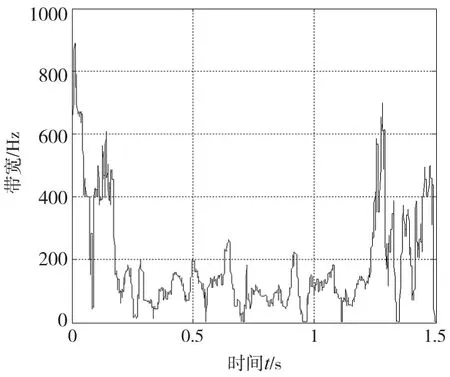
圖7　自適應濾波器Q的最終帶寬

4結論

本文針對PMLSM伺服系統迭代學習控制過程中放大非重復性擾動問題，提出了自適應濾波ILC方案。PD型ILC與反饋控制相結合保證了系統收斂性及跟蹤精度。加入的自適應濾波器Q的帶寬在時間軸上根據誤差的特征智能變化，盡可能的保留有用輸入信息的同時抑制擾動。實驗研究表明，自適應濾波ILC有效地抑制了擾動沿迭代軸的放大，與 PD型ILC相比，減小了位置誤差，提高了系統的魯棒性。

[參考文獻]

[1] 趙希梅，馬志軍，朱國昕. 永磁直線同步電動機自適應PD型迭代學習控制[J]. 沈陽工業大學學報，2016，38(1)：7-12

[2] 武志濤，李福云. 基于H∞擾動補償器的永磁直線電機伺服控制器設計[J]. 組合機床與自動化加工技術，2015(11)：67-70.

[3] 張宏偉，余發山，卜旭輝，等. 基于魯棒迭代學習的永磁直線電機控制[J]. 電機與控制學報，2012，16(6)：81-86.

[4] 楊俊友，師光洲，白殿春. 基于迭代學習的永磁直線伺服系統擾動抑制[J]. 組合機床與自動化加工技術，2014(8)：59-66.

[5] 于少娟，齊向東，吳聚華. 迭代學習控制理論及應用[M]. 北京：機械工業出版社，2005.

[6] 宋亦旭，王春洪，尹文生，等. 永磁直線同步電動機的自適應學習控制[J]. 中國電機工程學報，2005，25(20)：151-156.

[7] Teo C S，Tan K K，Lim S Y. Dynamic geometric compensation for gantry stage using iterative learning control[J]. IEEE Transactions on Instrumentation and Measurement，2008，57(2)：413-419.

[8] Rotariu I，Steinbuch M，Ellenbroek R. Adaptive iterative learning control for high precision motion systems[J]. IEEE Transactions on Control System Technology，2008，16(5)：1075-1082.

[9] 楊俊友，劉永恒，白殿春，等. 基于迭代學習與小波濾波器的永磁直線伺服系統擾動抑制[J]. 電工技術學報，2013，28(3)：87-92.

[10] Butcher M， Karimi A， Longchamp R. A statistical analysis of certain iterative learning control algorithms [J]. International Journal of Control，2008，81(1)：156-166.

[11] Madady A. An extend PID type iterative learning control[J]. International Journal of Control，Automation，and Systems，2013，11(3)：70-481.

(編輯趙蓉)

Adaptive Filtering Iterative Learning Control for Permanent Magnet Linear Synchronous Motor

ZHAO Xi-mei, MA Zhi-jun, ZHU Guo-xin

(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)

Abstract：An adaptive filtering iterative learning control(ILC) scheme was proposed for the non-repetitive disturbances amplification in ILC for permanent magnet linear synchronous motor(PMLSM). The control scheme is composed of a direct feedback loop and an additional ILC loop. The servo system gets fast convergence and has a high control precision by combining the design of open loop PD type learning law on the ILC circuit with the feedback controller. The design of bandwidth in the time axis variation of adaptive filter Q according to the signal time-frequency distribution information from pseudo Wigner-Ville distribution, avoid the amplification of non-repetitive disturbances in the iterative learning process. The experimental results indicate that the proposed control scheme improve the position tracking precision at the same time, effectively enhances the robustness of the system.

Key words：permanent magnet linear synchronous motor; iterative learning control; adaptive filter; robustness; tracking accuracy

文章編號：1001-2265(2016)05-0107-03

DOI:10.13462/j.cnki.mmtamt.2016.05.029

收稿日期：2015-07-10

*基金項目：國家自然科學基金(51175349)；遼寧省教育廳科學技術研究項目(L2013060)

作者簡介：趙希梅(1979—)，女，吉林德惠人，沈陽工業大學副教授，博士，研究領域為直線伺服，數控技術，魯棒控制，(E-mail)zhaoxm_sut@163.com。

中圖分類號：TH166;TG659

文獻標識碼：A