非均勻采樣非線性系統的模糊控制器設計
張 鐸,馬照瑞,朱訓林
(1.北京理工大學 計算機學院,北京 100081;2.鄭州輕工業學院 計算機與通信工程學院,河南 鄭州 450002;3.鄭州大學 數學與統計學院,河南 鄭州 450001)
?
非均勻采樣非線性系統的模糊控制器設計
張鐸1,馬照瑞2,朱訓林3
(1.北京理工大學 計算機學院,北京 100081;2.鄭州輕工業學院 計算機與通信工程學院,河南 鄭州 450002;3.鄭州大學 數學與統計學院,河南 鄭州 450001)
摘要:研究了滿足局部Lipschitz條件的非線性系統非均勻采樣模糊狀態反饋控制問題。通過定義一個和采樣時刻相關的Lyapunov函數,結合凸組合技術,得到了保證系統漸近穩定的充分性判據,并給出了相應的狀態反饋控制器設計方法。以線性矩陣不等式形式給出的設計條件易于檢驗,與現有的方法相比,設計過程簡單易行。算例驗證了本文所得結果的有效性。
關鍵詞:T-S模糊系統;采樣控制;狀態反饋;線性矩陣不等式
0引言
T-S模糊模型自1985年被提出以來,由于其特殊的規則后件引發了廣泛的研究。文獻[1]分析了模糊系統對一類可積函數的泛逼近性。結合采樣特性,文獻[2]討論了非線性網絡控制系統的量化保成本控制問題。文獻[3]研究了T-S模糊連續系統的模糊采樣控制問題。文獻[4]擴展了文獻[5]中給出的Lyapunov函數構造方法,得到了保守性更小的穩定化條件。但是,正如文獻[6]指出的那樣,現有的T-S模糊采樣控制器設計方法只能導出線性的控制器。為得到非線性的模糊控制器,文獻[7]提出了一種 “精確的離散設計方法”,該方法的缺點是系統離散化過程復雜,且采樣周期必須固定(即均勻采樣)。文獻[8]將模糊隸屬度函數的異步誤差當成系統模型的不確定性,由于模糊隸屬度函數異步誤差的上界難以精確獲取,因此這種方法也有一定的局限性。
本文考慮了一類滿足局部Lipschitz條件的非線性系統的采樣控制問題,給出了松散的穩定性條件和新的模糊狀態反饋控制器設計方法。與現有的方法相比,本文方法無需系統離散化,而且也不涉及模糊隸屬度函數的異步誤差上界,使設計過程得以簡化。
1問題描述
考慮如下一類非線性系統:
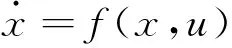
(1)
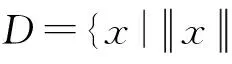

(2)
本文采用基于采樣的模糊狀態反饋控制器Kj(j=1,2,…,r),控制信號為:
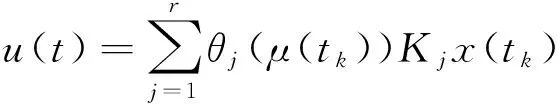
(3)
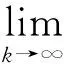
假設1在D上,非線性向量值函數f關于x滿足Lipchitz條件[7],即:
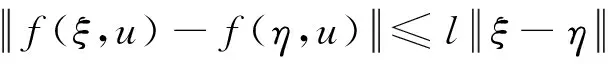
(4)
其中:l為一個常數,l>0。
假設2采樣區間長度ηk:=tk+1-tk是有界的,即:
0<ηk≤η,?k=0,1,2,… ,
(5)
其中:η為一個正的常數。
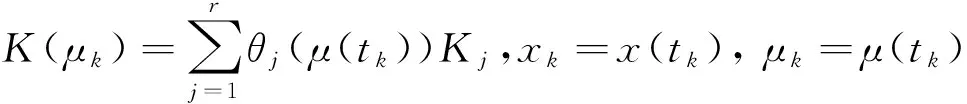
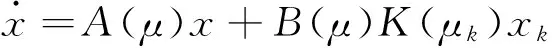
(6)
若令p=f(x,uk)-f(xk,uk),即可得:
pTp≤l2(x(t)-xk)T(x(t)-xk)。
(7)
且注意到:
u(t)=u(tk),?t∈[tk,tk+1),
以及
f(xk,uk)=A(μk)xk+B(μk)uk,
因此,閉環系統可寫為:
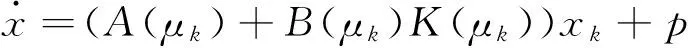
(8)
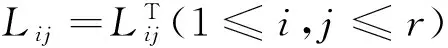
Lij+Lji<0
都成立的話,則不等式
(9)
也成立[9]。
2主要結果
首先,給出保證閉環系統(8)漸近穩定的充分性條件。
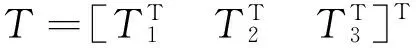
(10)
和
(11)
成立,則閉環系統(8)是漸近穩定的。其中:
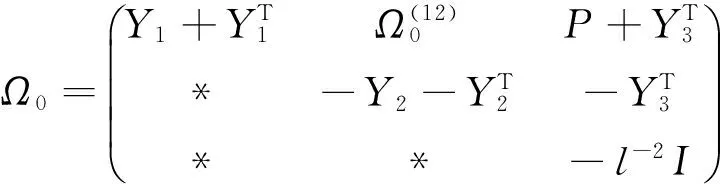
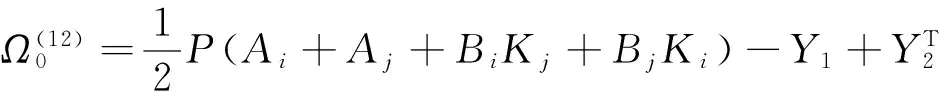


證明取Lyapunov函數為:
V(t)=V1(t)+V2(t)+V3(t)+V4(t),
(12)
其中:
V1(t)=xT(t)Px(t);

V3(t)=(ηk-(t-tk))(t-tk)xT(tk)Ux(tk);
V4(t)=(η-(t-tk))[x(t)-xk]T[x(t)-xk]。
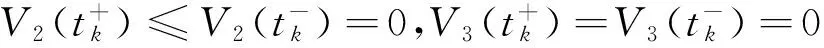
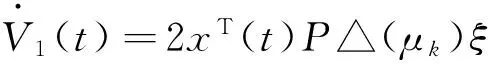
(η-(t-tk))ξT△(μk)TS△(μk)ξ+(t-tk)ξTYS-1YTξ+2ξTY[x(t)-xk];
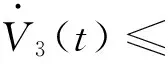
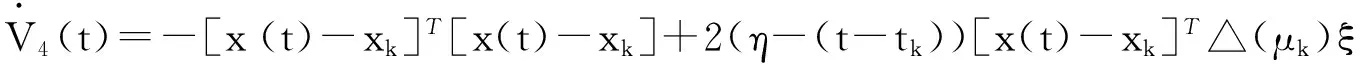
注意到:
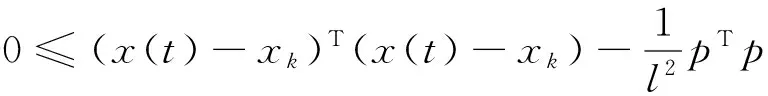
2[x(t)-xk]T△(μk)ξ≤[x(t)-xk]TW[x(t)-xk]+ξT△(μk)TW-1△(μk)ξ,
所以有:
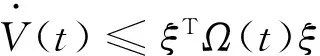
(13)
其中:
Ω(t)=Ω4(μk)+(η-(t-tk))Ω5(μk)+(t-tk)Ω6;
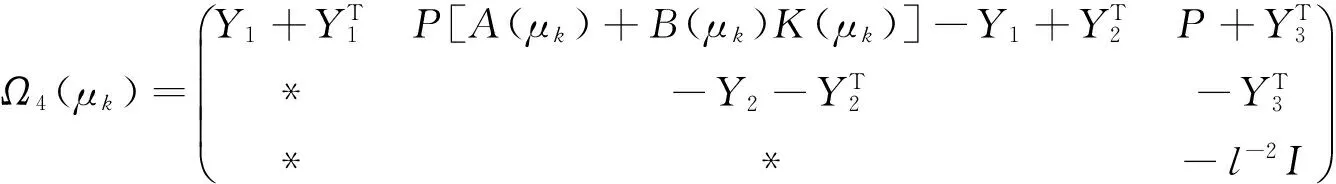

Ω6=YS-1YT-Ω1。
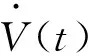
注意到Ω(t)是關于Ω5(μk)和Ω6的一個凸組合,所以Ω(t)<0對任意的0≤t-tk≤η成立,當且僅當
Ω4(μk)+ηΩ5(μk)<0
(14)
和
Ω4(μk)+ηΩ6<0
(15)
同時成立。由引理2可知,式(14)和式(15)分別等價于:
(16)
和
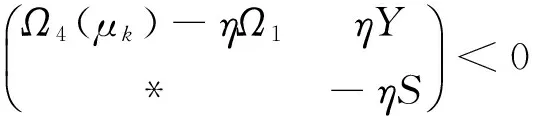
(17)
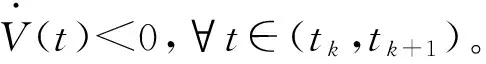
證畢。
注1:與文獻[4,10]類似,在定理1的證明中,利用系統的采樣特性,定義了一個與采樣時刻相關的Lyapunov函數(12)。隨著V4(t)的引入,結合非線性向量值函數f關于x滿足Lipchitz條件,以及凸組合技術,導出了閉環系統(8)漸近穩定的一個線性矩陣不等式判據。
注2:與文獻[7]一樣,本文也假定非線性向量值函數f在D上關于x滿足Lipchitz條件。但是,本文的處理方法與文獻[7]完全不同,系統不需要進行離散化處理,從而大大簡化了分析過程;同時,采樣區間允許是時變的。注意到文獻[8]要求每個隸屬度函數在每個采樣區間[tk,tk+1)的變化幅度是已知的,即:
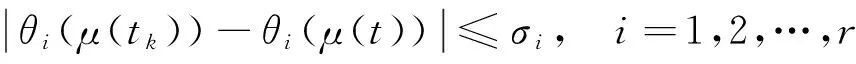
其中:σi為滿足0≤σi≤1的常數。正如文獻[8]的注1指出的那樣,目前,尚無一個系統的方法能夠獲取這樣的上界σi。與文獻[8]不同,本文沒有涉及模糊隸屬度函數的變化幅度。
令:
Q=P-1; R=QUQ;
T1=QY1Q; T2=QY2Q; T3=Y3Q;
Z=QSQ; Vj=KjQ (j=1,2,…,r)。
對定理1中矩陣不等式(10)左邊分別左乘和右乘對角矩陣diag{Q,Q,I,S-1,I,W-1},可得:

(18)
其中:Ω3已在定理1中定義,且
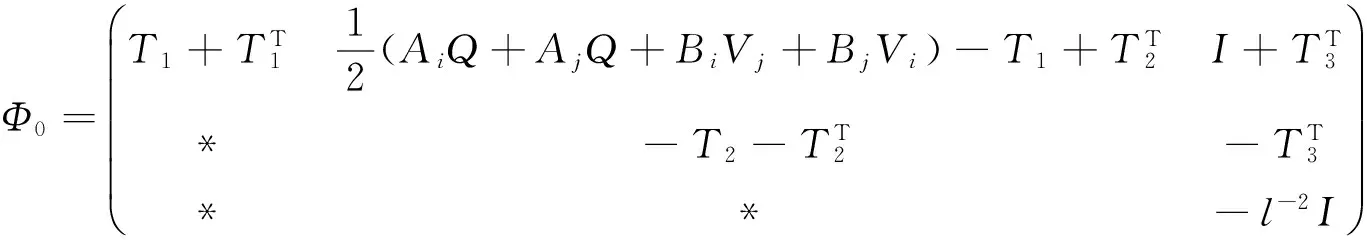
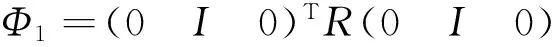
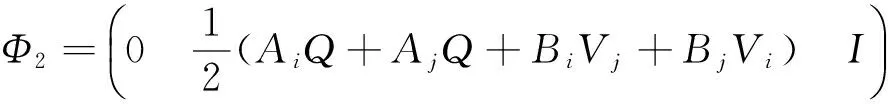
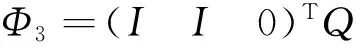
類似地,定理1中矩陣不等式(11)左邊分別左乘和右乘對角矩陣diag{Q,Q,I,I},并依引理2可得:
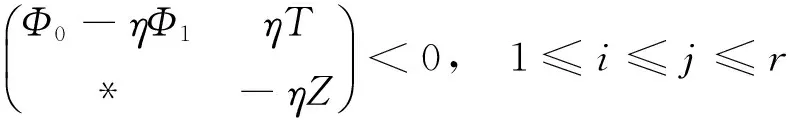
(19)
對于式(18)中的非線性項-ηQZ-1Q,利用關系式(Q-Z)Z-1(Q-Z)≥0,可得:
-ηQZ-1Q≤-2ηQ+ηZ。
(20)
同理可得:-ηW-1≤-2ηI+ηW。
因此,有如下定理:
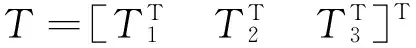
(21)
和式(19)成立,則閉環系統(8)是漸近穩定的。此時,系統的狀態控制器增益Kj(j=1,2,…,r)可由下式給出:
Kj=VjQ-1。
注3:定理2給出了閉環系統(8)的可鎮定條件。與文獻[7]不同,本文的矩陣不等式非常簡潔,采樣區間允許是時變的。同時,與文獻[8]不同,在定理2的鎮定條件中沒有引入調節參數,這樣就簡化了控制器設計過程。
3算例
考慮一個慣性輪倒立擺系統,它的狀態方程可以表示成非線性系統(1)的形式,非線性函數f[7,11]如下:
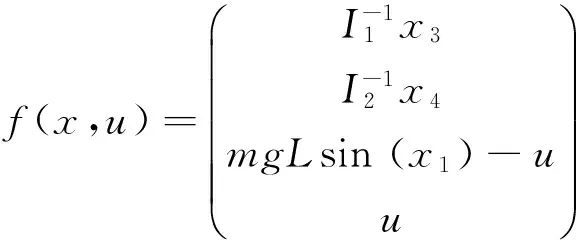
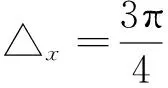
其中:I1=0.1;I2=0.2;mgL=10;a1=1;a2=sin (△x)/△x。
文獻[7]中只給出了η=0.001,而由定理2可得η=0.003,這表明本文所給方法的保守性較小。當η=0.001時,由定理2的矩陣不等式組解得模糊狀態反饋控制器增益為:


設系統狀態初值為(0.60-0.580.10-0.20)T時,使用上述的模糊狀態反饋控制器增益,則系統的狀態響應曲線如圖1所示。
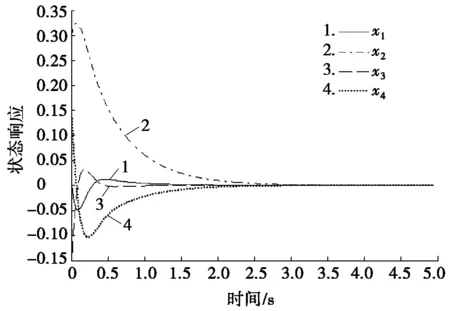
圖1 系統的狀態響應曲線
從圖1中容易看出:閉環系統是漸近穩定的。這表明本文給出的采樣模糊狀態反饋控制器設計方法切實可行。
4結束語
本文研究了一類非線性系統的采樣模糊狀態反鎮定問題。通過構造合適的Lyapunov函數,利用采樣特性以及矩陣不等式技術,推導出穩定性條件,并在此基礎上提出了新的控制器設計方法,給出了線性矩陣不等式形式的可鎮定判據。與現有的方法相比,本文方法無需系統的離散化,也沒有引入調節參數,簡化了設計過程。數值算例驗證了本文方法的有效性。
參考文獻:
[1]段晨霞,王貴君.模糊系統中方形分片線性函數依K-積分模的泛逼近性[J].天津師范大學學報(自然科學版),2012,32(3):1-5.
[2]褚紅燕,費樹岷,岳東.基于T-S模型的非線性網絡控制系統的量化保成本控制[J].控制與決策,2010,25(1):31-42.
[3]賈新春,張靜梅,李宏峰,等.Takagi-Sugeno模糊連續系統的模糊采樣控制[J].控制理論與應用,2007,24(1):69-74.
[4]ZHU X L,CHEN B,YUE D,et al.An improved input delay approach to stabilization of fuzzy systems under variable sampling[J].IEEE transactions on fuzzy systems,2012,20(2):330-341.
[5]NAGHSHTABRIZI P,HESPANHA J P,TEEL A R.Exponential stability of impulsive systems with application to uncertain sampled-data systems[J].System & control letters,2008,57(5):378-385.
[6]KIM D W,LEE H J.Comments on “T-S fuzzy-model-based robustH∞design for networked control systems with uncertainties”[J].IEEE transactions on industry information,2009,5(4):507.
[7]KIM D W,LEE H J.Sampled-data observaer-based out-feedback fuzzy stabilization of nonlinear systems:exact discrete-time design approach [J].Fuzzy sets and systems,2012,201:20-39.
[8]ZHU X L,CHEN B,YUE D,et al.H∞stabilization criterion with less complexity for nonuniform sampling fuzzy systems[J].Fuzzy sets and systems,2013,225:58-73.
[9]TUAN H D,APKARIAN P,NARIKIYO T,et al.Parameterized linear matrix inequality techniques in fuzzy control system design[J].IEEE transactions on fuzzy systems,2001,9(2):324-332.
[10]FRIDMAN E,SEURET A,RICHARD J.Robust smapled-data stabilization of linear systems:an input delay approach[J].Automatica,2004,40(8):1441-1446.
[11]ORTEGA R,SPONG M W,GMEZ-ESTERN F,et al.Stabilization of a class of underactuated mechanical system via interconnection and damping assignment[J].IEEE transactions on automatic control,2002,47(8):1218-1233.
基金項目:國家自然科學基金項目(61174085,61374063);河南省教育廳科技攻關基金項目(14A520017,14A520059)
作者簡介:張鐸(1995-),男,河南鄢陵人,本科生;馬照瑞(1978-),通信作者,男,河南輝縣人,講師,碩士,主要研究方向為網絡控制和無線傳感.
收稿日期:2016-03-19
文章編號:1672-6871(2016)04-0050-06
DOI:10.15926/j.cnki.issn1672-6871.2016.04.011
中圖分類號:TP273
文獻標志碼:A

