基于DAPSO-UGM(1,1)模型的物流需求預測

張連偉,何　梁,耿立艷

(石家莊鐵道大學　經濟管理學院,河北　石家莊　050043)

基于DAPSO-UGM(1,1)模型的物流需求預測

張連偉,何梁,耿立艷

(石家莊鐵道大學經濟管理學院,河北石家莊050043)

[摘要]物流需求預測的準確性對我國的經濟發展具有重要作用。為提高物流需求的預測精度,文章利用動態自適應粒子群優化算法(DAPSO)優化無偏灰色預測模型[UGM(1,1)]參數,構建DAPSO-UGM(1,1)模型預測物流需求。以我國物流需求為例,證明了DAPSO-UGM(1,1)模型的有效性,并預測了未來我國的物流需求,為物流需求預測提供了新的方法。

[關鍵詞]動態自適應粒子群算法；無偏灰色預測模型；物流需求預測

[DOI]10.13939/j.cnki.zgsc.2016.10.010

隨著經濟的發展,物流需求在交通網絡規劃、物流設施投資和物流規劃等方面扮演著越來越重要的角色,因此準確的物流需求預測對我國的經濟發展具有重要的意義。現有的預測模型中較為常用的是時間序列、回歸分析和灰色預測模型,由于時間序列和回歸分析預測模型在實際應用中考慮的相關因素較少,因此預測誤差相對較大,而灰色預測模型在預測時需要的數據較少,預測精度較高且適用于中長期的預測,所以不少學者開始將灰色預測(GM(1,1))模型引入物流需求預測[1,2]中,而在物流需求預測中GM(1,1)模型[3]是最常用的。在GM(1,1)模型的基礎上,又出現了預測性能優于GM(1,1)模型的無偏灰色預測(UGM(1,1))模型[4],但該模型隨著發展系數的變大,性能有變差的趨勢,進而導致物流需求的預測精度下降。粒子群優化(PSO)算法是一種群智能優化算法[5],在參數優化方面得到廣泛應用。作為PSO算法的改進算法,動態自適應粒子群優化(DAPSO)算法[6]根據粒子早熟收斂程度和個體適應度值動態地調整慣性權重,提高了算法的收斂速度和精度。本文利用DAPSO算法優化UGM(1,1)模型的參數,以進一步提高物流需求預測的精度。

1無偏灰色預測模型

GM(1,1)模型是以“部分信息已知,部分信息未知”的“小樣本”“貧信息”的不確定性系統為研究對象,由已知的部分信息預測未知信息的一種模型。而無偏灰色預測(UGM(1,1))模型則對GM(1,1)模型做了進一步改進,消除了傳統GM(1,1)模型存在的固有偏差。UGM(1,1)模型的建模步驟如下：

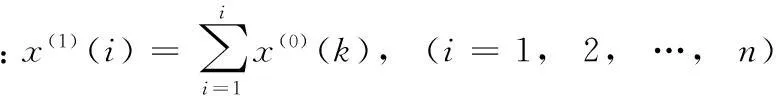
(1)

其中,a為發展灰度,u為內生控制灰度。通過最小二乘法求解參數列C=[au]T：

(2)

其中,B和Yn分別為：

(3)

建立原始數據序列模型：

(4)

(5)

2動態自適應粒子群優化算法

PSO算法是最近幾年內出現的迭代優化算法,首先給定一組初始值,然后根據已知函數確定適應值(fitness value)并且不斷地進行迭代優化,即模擬粒子在空間內按照一定的約束,進行相應的搜索,從而使得粒子找到本身的最優值,包括個體極值(pbest)和群體極值(gbest)。

設在D維空間中存在一個群體,該群體中包含n個粒子,第i個粒子的位置為Xi=(xi1,xi2, …,xiD)； 速度為Vi=(vi1,vi2, …,viD)； 當前搜索到的最優位置為Pi=(pi1,pi2, …,piD), 在群體中搜索得到的最優位置為Pg=(pg1,pg2, …,pgD)。將以上的各個量帶入目標函數,可以計算出函數的適應值,得到粒子狀態的更新公式為：

Vid=WVid+c1r1(Pid-Xid)+c2r2(Pid-Xid)

(6)

Xid=Xid+Vid

(7)

其中,i=1,2,…,s,d=1,2,…,D；W為慣性權重,c1、c2為學習因子,r1、r2是[0,1]的隨機數。式(6)中,反映了粒子先前速度的慣性大小,當W值較大時,全局搜索能力強,收斂速度快；當W值較小時,局部搜索能力強,解的精度高,收斂速度慢。所以,在一般的PSO算法中,W的值通常在0.1～0.9,為了使慣性權重對算法能否收斂更加準確,可采用一種基于群體早熟收斂程度和個體適應值來調整慣性權重的動態自適應粒子群算法。

2.1算法早熟收斂度評價

設粒子i的當前適應值為fi,當前適應值的平均值為favg,則有以下計算式：

(8)

(9)

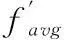
2.2自適應調整策略

PSO算法中,當搜索出現局部極值時,粒子停滯；當粒子群在局部極值附近運動較小時,根據其早熟收斂程度,可對W做動態自適應調整,調整方法為：

(1)fi比favg好。

(10)

(2)fi比favg好,但搜索效率差。

(11)

其中,Wmax為最大慣性權重,Wmin為最小慣性權重,m、Wmax分別為當前迭代次數和最大迭代次數。

(3)fi比favg差。

(12)

其中,參數k1主要影響算法的最大慣性權重,參數k2主要影響慣性權重的調節能力。

3DAPSO-UGM(1,1)模型

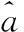
(13)

第二步：確定目標函數。以模型預測值與實際物流需求的誤差的平方和最小為目標函數。

(14)

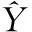
第三步：初始化每個粒子的位置和速度。

第四步：評價每個粒子的適應值。

第五步：得到每個粒子的pbest和gbest。

第六步：利用式(6)和式(7)更新各個粒子的位置和速度。

第七步：如果達到精度要求或者達到最大的迭代次數,輸出gbest及其適應值并停止迭代,否則返回第四步。

4模型應用

4.1數據選取

以貨運量作為物流需求的量化指標,選取2006—2013年我國貨運量數據,檢驗DAPSO-UGM(1,1)模型的預測效果。所用數據來源于《中國統計年鑒2014》。表1給出2006—2013年我國貨運量數據。由表1可知,我國2006—2013年貨運量基本呈指數增長趨勢,因而采用DAPSO-UGM(1,1)模型進行分析和預測是合理的。

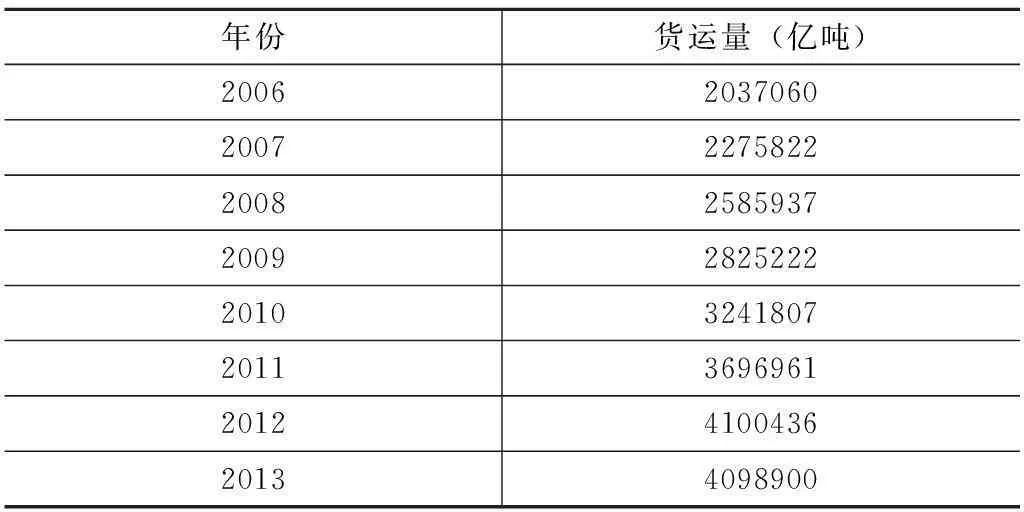
表1　2006—2013年物流需求

4.2模型檢驗

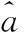
由表2可知,DAPSO-UGM(1,1)模型的最大、最小相對誤差為3.39%和0.02%,分別小于GM(1,1)模型、UGM(1,1)模型和PSO-UGM(1,1)模型的對應值,同時其平均相對誤差也明顯小于其他三模型,這有力證明了DAPSO-UGM(1,1)模型的預測精度優于其他三模型。因此,基于DAPSO算法優化的UGM(1,1)是一種有效的物流需求預測方法。

4.3外推預測

將DAPSO-UGM(1,1)模型應用于未來物流需求預測中,利用DAPSO-UGM(1,1)模型預測2014—2020年的物流需求,預測結果如表3所示。從表3可以看出,未來7年物流需求將呈現出先增后減的變化趨勢。

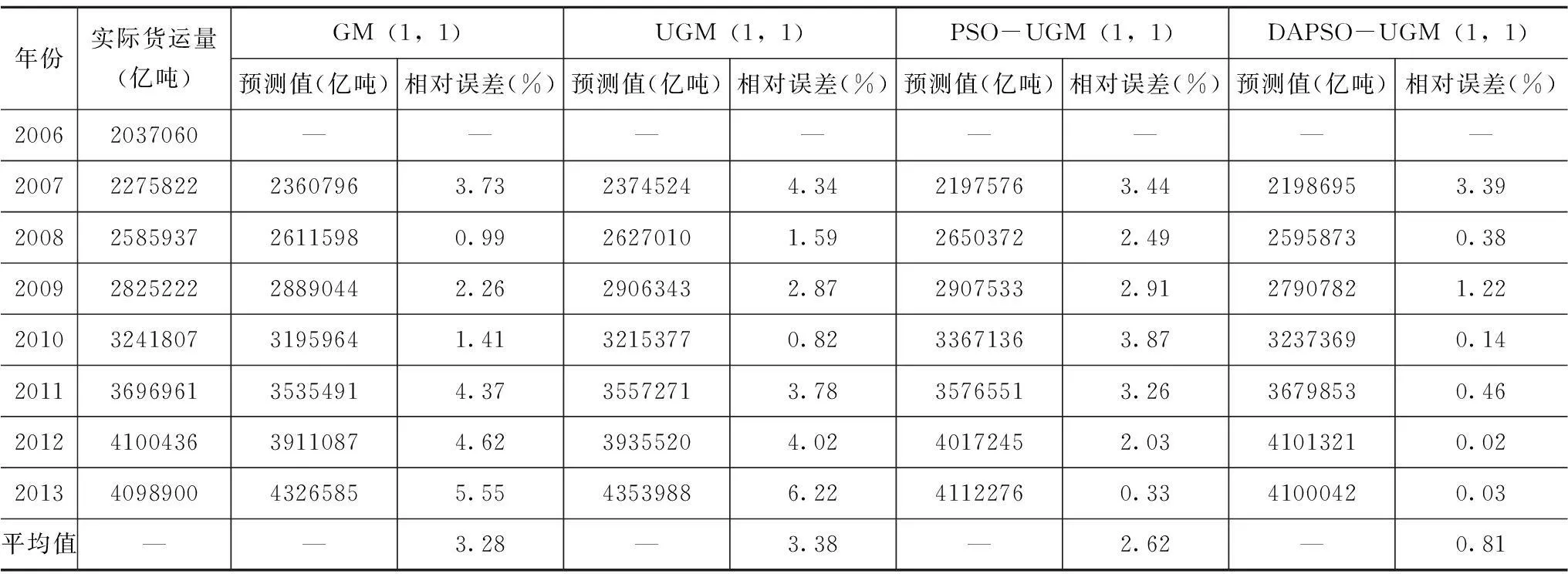
表2　檢驗結果比較

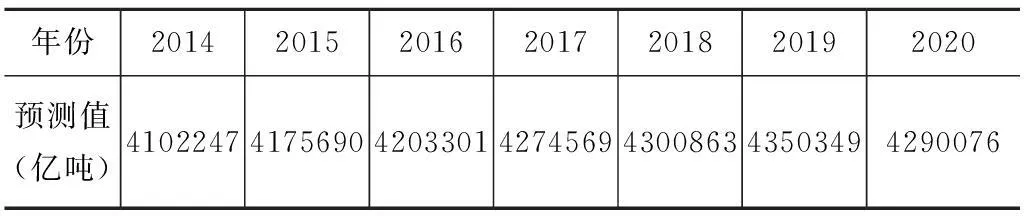
表3　2014—2020年物流需求

5結論

本文結合DAPSO算法與UGM(1,1)模型,構建DAPSO-UGM(1,1)物流需求預測模型,利用DAPSO算法優化UGM(1,1)模型參數。通過對我國物流需求的實例分析,驗證了DAPSO-UGM(1,1)模型是一種有效的物流需求預測方法,并利用該模型預測了未來我國的物流需求。

參考文獻:

[1]張潛.物流需求回收預測及其實證分析[J].哈爾濱工業大學學報：社會科學版,2010,12(1): 84-89.

[2]王小麗.基于多因素灰色模型的物流需求量預測[J].統計與決策,2013(14): 86-87.

[3]劉思峰.灰色系統理論及其應用[M].北京：科學出版社,2014.

[4]劉鵠,吉培萊,鄒紅波.無偏灰色預測模型在邊坡變形預測中的應用[J].三峽大學學報：自然科學版,2007,29(1): 43-45.

[5]張芳芳,王建軍,張勇.少控參數的分層式骨干粒子群優化算法[J].系統工程理論與實踐,2015,35(12): 3217-3224.

[6]盛桂敏,薛玉翠,張博陽.動態自適應粒子群優化算法[J].綏化學院學報,2011,31(6): 190-192.

[基金項目]2015年度大學生創新創業訓練計劃項目“物流需求的智能預測方法及實證研究”；國家自然科學基金青年項目(項目編號：61503261);河北省軟科學研究計劃項目(項目編號：15456106D)；河北省社會科學發展重點研究課題(項目編號：2015020206)。