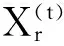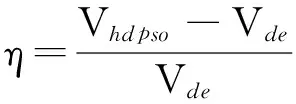帶時間窗裝卸一體化車輛路徑問題的混合離散粒子群優化算法

周　蓉　沈維蕾　劉明周　趙　韓

合肥工業大學，合肥，230009

帶時間窗裝卸一體化車輛路徑問題的混合離散粒子群優化算法

周蓉沈維蕾劉明周趙韓

合肥工業大學，合肥，230009

摘要：為了同時實現總配送成本最低、車輛數最少和車輛行駛距離最短等目標，考慮車輛指派成本及運輸路徑成本的相對重要性，建立了帶時間窗裝卸一體化車輛路徑問題的混合整數規劃模型。針對該問題搜索空間的離散性和求解算法的局部收斂性，提出了一種混合離散粒子群求解算法。算法基于客戶排列的直觀無分段大路徑解表示法，采用改進深度優先搜索分割法對問題解進行解碼與評價；嵌入一種變鄰域下降搜索程序并在個體粒子每次迭代時以一定概率選擇執行，利用混合粒子群算法在多鄰域深度搜索和在全局空間廣度搜索進行尋優，同時應用模擬退火思想和比例選擇性變異最差個體來改善個體搜索停滯現象。采用兩個不同目標算例進行尋優測試，驗證了所提算法的可行性和有效性。

關鍵詞：帶時間窗車輛路徑問題；裝卸一體化；離散粒子群優化算法；變鄰域下降搜索

0引言

車輛在完成客戶配送或取貨過程中普遍存在回程或去程空載現象，如何有效整合正向和逆向物流，減少運輸資源浪費，降低物流運作成本，是逆向物流系統規劃中的重要決策問題。當客戶同時具有送貨和取貨需求時存在兩種車輛服務策略，一種策略是車輛將貨物送至客戶的同時從該處取走貨物，車輛裝卸操作同時完成；另一種策略是車輛完成所有送貨需求后按原路徑返回完成取貨需求，車輛裝卸操作分時完成。這兩種策略問題分別稱為裝卸一體化車輛路徑問題和帶回程車輛路徑問題[1-2]。如果帶回程問題去程的取貨量或回程的送貨量為零，則問題轉變為裝卸一體化車輛路徑問題。文獻[2]的研究結果表明，裝卸一體化車輛路徑問題較帶回程車輛路徑問題具有更低的運作成本。裝卸一體化車輛路徑問題最早由Min[3]提出，用于解決1個中心圖書館與22個鄉村圖書館之間的圖書發送與回館問題。有關該問題的研究文獻比較多，但因其是NP-Hard問題，求解方法大多集中在啟發式方法和元啟發方法。啟發式方法主要以經典C-W節約算法為基礎，考慮不同的啟發式規則進行求解[4-6]；元啟發方法以群體智能為基礎，考慮不同的信息傳遞與更新方式進行求解[7-8]。現實中客戶對送貨與取貨通常有一定的時間要求，即要求車輛在指定的時間范圍內完成裝卸操作，這就是帶時間窗裝卸一體化車輛路徑問題(vehicleroutingproblemwithtimewindowsandsimultaneouspickupanddelivery，VRPTWSPD)。該問題較裝卸一體化車輛路徑問題更能反映實際情況，因而具有更為廣闊的應用前景，但由于決策目標、決策影響因素和約束條件較多造成求解困難，目前相關研究還比較少。

現有VRPTWSPD相關研究多以最小化車輛行駛距離為目標，雖然少數研究增加了車輛數目方面的分析，但缺乏對總配送成本、車輛數目、車輛行駛距離等多種目標的系統性分析。如：Angelelli等[9]以最小化車輛行駛距離為目標，采用分支定界算法解決了20個客戶的小規模VRPTWSPD問題；Lai等[10]運用改進的差分進化算法求解了相同目標問題，并分別采用由8個客戶和40個客戶組成的兩個不同規模算例進行了算法準確性和有效性驗證；Wang等[11]以最小化車輛數目、最小化車輛行駛距離為目標，提出采用聯合進化遺傳算法進行求解，并將Solomon的經典VRPTW(vehicleroutingproblemwithtimewindows)問題集擴展為65個10～100個客戶規模的VRPTWSPD算例，計算結果證明該方法較基本遺傳算法和數學規劃工具Cplex具有更好的穩定性。此外，王超等[12]還采用改進的模擬退火算法，以文獻[11]擴展的部分VRPTWSPD問題為測試算例，證明了該方法在部分算例中較文獻[11]的聯合進化算法求解性能更好；Boubahri等[13]以最大化站點服務能力為目標，提出采用多蟻群算法對多校車站點的VRPTWSPD問題進行求解，但未進行算法驗證。

粒子群優化(particleswarmoptimization，PSO)算法是一種基于群體智能的自適應元啟發算法，在許多車輛路徑與調度問題的求解應用中已被證明具有良好的優化性能[7,14-15]。PSO算法在搜索處理后期階段容易出現早熟收斂從而陷入局部最優，因此通常與局域搜索相結合，利用其拓展局域深度搜索的特點提高整體搜索性能[7,15]。受到該思想的啟發，本文將變鄰域下降搜索程序嵌入基本離散粒子群算法，提出一種混合離散粒子群算法求解包含多種目標的VRPTWSPD問題，并通過算例仿真和結果對比驗證了所提出算法的可行性和有效性。

1問題描述與模型

VRPTWSPD問題可以描述為：物流中心擁有一定數量的相同車輛，車輛從配送中心出發，在一定時間內完成確定數量客戶集的送貨與取貨后返回物流中心。每個客戶的送貨與取貨由同一車輛同時完成。每個客戶具有確定的位置及獨立的服務時間窗，每輛車在指定的時間范圍離開和返回物流中心。要求合理安排車輛配送路線，在派出車輛數目最小、車輛行駛距離最短情況下，實現總配送成本最小。采用符號體系描述如下：假設物流中心共有N個客戶，采用i、j表示客戶編號(i = 1, 2, …, N; j = 1, 2, …,N), 0表示物流中心；Z為總配送成本；客戶的送貨量和取貨量分別為di、pi；客戶之間的距離為cij，物流中心到客戶i的距離為c0i；車輛單位距離行駛成本為g，單車指派成本為f，最大裝載量為Q；車輛總數為K，車輛k(k = 1, 2, …, K)到達客戶i的時間為Tik，在節點i的等待時間為tik，在i、j兩個節點之間的行駛時間為tijk，離開客戶i時車上載重量為Uik，離開和返回物流中心的時間分別為L0k、R0k(也可以由車輛的最大行駛距離L進行限制)；客戶i要求的服務時間窗為[ai,bi]，服務時間為si；物流中心0對車輛的時間窗要求為[a0,b0]；m、n分別為車輛指派成本、運輸路徑成本對總配送成本的重要性指數，m∈[0,1)，n∈(0,1]。

根據上述描述，建立VRPTWSPD問題的混合整數規劃模型如下：

(1)

滿足約束條件：

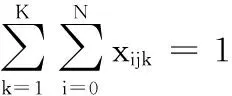
(2)

(3)

?j=1,2,…,N

(4)

?i=0，1,…,N;k=1,2,…,K

(5)

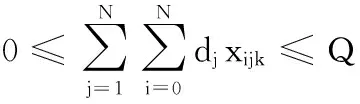
(6)

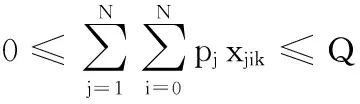
(7)

?i=1,2,…,N;j=0,1,…,N

(8)

tik=max(ai-Tik,0)

?i=1,2,…,N;k=1,2,…,K

(9)

ai≤Tik+tik≤bi

?i=1,2,…,N;k=1,2,…,K

(10)

a0≤L0k?k=1,2,…,K

(11)

R0k≤b0?k=1,2,…,K

(12)

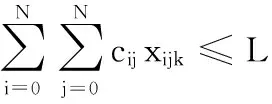
(13)

(14)

?i,j=0,1,…,N;k=1,2,…,K

其中，式(1)為考慮了車輛指派成本、運輸路徑成本的總配送成本Z最小目標，隱含車輛數目最小、車輛行駛距離最短兩個子目標；式(2)確保每個客戶只被服務一次且僅由一輛車服務；式(3)確保使用車輛數不超過車輛總數K；式(4)為流量守恒式，即到達和離開每個客戶的車輛相同；式(5)～式(7)為容量約束；式(8)～式(10)為客戶的時間窗約束，其中式(8)中的M為一個很大的正數；式(11)～式(12)為物流中心的時間窗約束；式(13)確保車輛的最大行駛距離不超過L；式(14)為決策變量屬性約束。調整m和n的值，可以使式(1)目標發生改變。如令m = 0、n = 1，模型目標為行駛距離最小化，與文獻[10]相同；令n = 1- m，模型目標為配送成本最小化，與文獻[11]相同。

2算法設計

2.1離散粒子群算法基本原理

離散粒子群算法通過重新定義粒子操作算子[16]，用問題的一個排列作為粒子的一個位置，用問題的所有排列構成問題的搜索空間，并通過遺傳、變異和交叉操作，綜合粒子的當前狀態、個體思考及社會合作三部分信息實現粒子位置更新，其位置更新公式為[15]

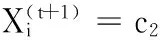
(15)

2.2混合離散粒子群算法

本文將變鄰域下降搜索引入離散粒子群算法作為個體粒子的一種概率變異，通過擴大局域搜索空間實現個體深度搜索，從而提高群體尋優能力。

2.2.1解的表示、解碼與評價

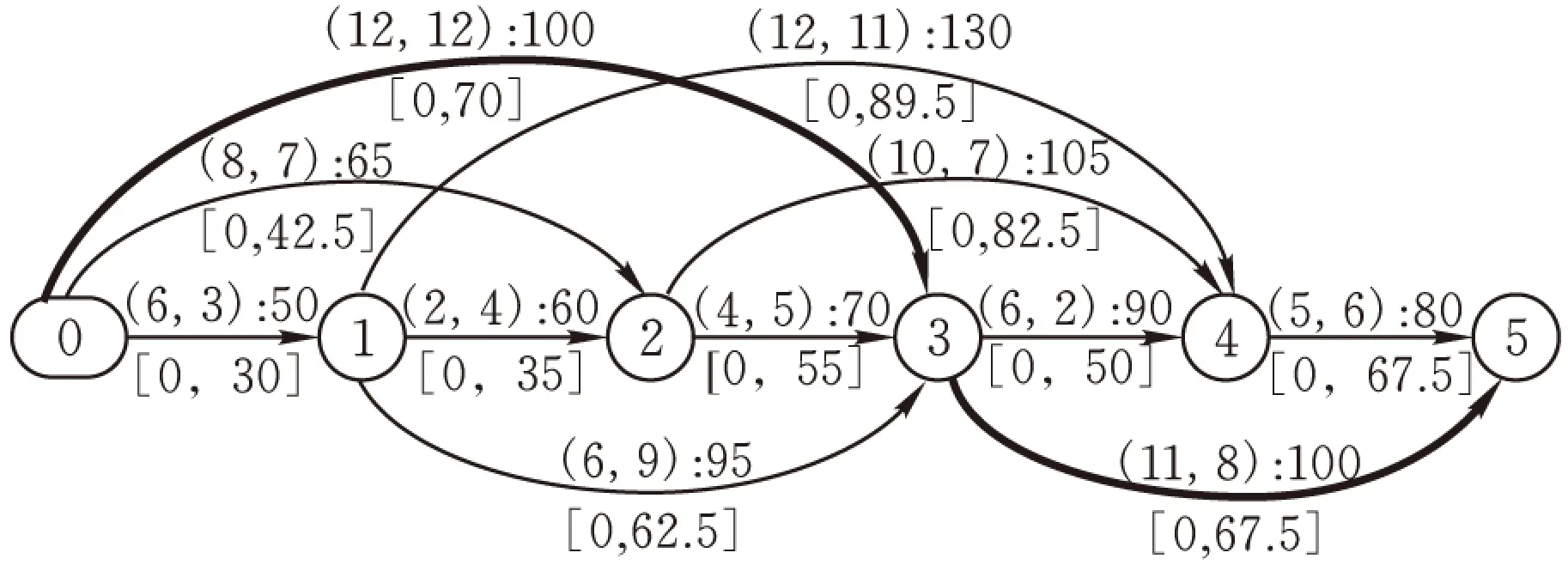
(1)解的表示。產生N個1 ～ N之間的互不重復自然數的排列，作為具有N個客戶的帶時間窗裝卸一體化車輛路徑問題的抽象解。該抽象解是一條以自然數序列表示客戶服務順序的無分段大路徑[17]，對于單車場車輛路徑問題通常在序列最前面加上0表示帶物流中心的大路徑。大路徑解圖示方法包括直觀圖和有向無圈圖，直觀圖給出物流中心及所有客戶的地理位置、客戶的送貨與取貨需求量、客戶及物流中心的服務時間窗等信息，如圖1a所示(圖中N = 5)；有向無圈圖給出客戶之間滿足約束條件的所有可行配送路徑的相關信息，如圖1b所示。

有向無圈圖(圖1b)中弧(i,j)為大路徑X={0,1,…,N}上第i個節點與第j個節點之間的可行配送路徑，表示車輛從物流中心出發依次服務第i +1、i +2、…、j -1、j個節點后返回物流中心。可行配送路徑滿足車容量、客戶及物流中心時間窗、車輛最大行駛距離等相關約束。設弧(i,j)上車輛的行駛距離為Dij，總配送成本為zij，其計算式如下：

(16)

zij=mDX(i+1,j)g+nf

(17)

(2)解碼。大路徑解碼也稱為大路徑分割，通過采用標簽管理方式對各節點進行標記，然后根據標記信息將大路徑上的客戶分別劃入不同的車輛配送路徑中，從而得到各車的配送方案(也稱作子路徑)。大路徑分割思想最先由Beasley[18]提出并應用于求解車輛路徑問題的先路徑后叢聚啟發式算法中，后被Prins[17]拓展用于求解VRP問題的遺傳算法中。Duhamel等[19]將大路徑分割方法分為廣度優先搜索和深度優先搜索兩種，其中深度優先搜索以其搜索速度快被廣泛用于VRP問題的元啟發方法中[17,19-20]。

根據VRPTWSPD問題的客戶雙重需求特性以及相關約束條件，包括車輛的最大載重量約束、客戶要求服務的時間窗約束，對文獻[20]的深度優先搜索方法進行修改，使其適用于VRPTWSPD問題的大路徑分割。該方法分為兩階段：第一階段構造有向無圈圖并給每個節點創建成本和距離標簽，確定每個節點上成本標簽的最小值，推斷各節點的前繼節點。第二個階段根據最后一個節點的前繼節點信息，逐個向前提取各節點的標簽信息，根據最小化總配送成本目標產生最優路徑方案。

對大路徑X={0,1,…,N}，若(i,j)為其有向無圈圖G(X)上的一段可行弧，Pi、Vi和Di分別為節點i的前繼節點標簽、總配送成本標簽與總行駛距離標簽，Pj、Vj和Dj分別為節點j的前繼節點標簽、總配送成本標簽與總行駛距離標簽，則存在以下關系式：Pj=i，Vj=Vi+zij,Dj=Di+DX(i+1,j)。以圖1為例，設車輛最大裝載量Q=12，單車指派成本f=10，車輛單位距離行駛成本g=1,車輛行駛速度v=2,車輛在每個節點的服務時間s=10,大路徑X={0,1,2,3,4,5};弧(0,2)表示路徑0-1-2-0，節點2的前繼節點標簽P2=0，假設m =n= 1，節點2的總配送成本標簽V2=V0+z02=0+65=65，節點2的總行駛距離標簽D2=D0+DX(1,2)=0+55=55；弧(2,4)表示路徑0-3-4-0,節點4的前繼節點標簽P4=2，節點4的總配送成本標簽V4=V2+z24=65+105=170，節點4的總行駛距離標簽D4=D2+95=55+95=150。根據圖1b中的黑色加粗弧可知，當V5=V3+z35=100+100=200時，大路徑X的最優分割為0-1-2-3-0、0-4-5-0，從而得到最優配送方案如圖1c所示。

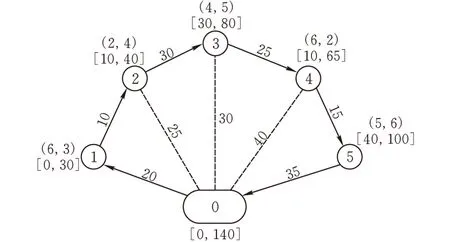
(a)直觀圖

(A,B):C[D,E]A:路徑上的總配送裝載量; B:路徑上的總集貨裝載量;C:路徑上的總成本; D:車輛離開物流中心的時間;E:車輛返回物流中心的時間(b)有向無圈圖

(c)最優方案圖 1　大路徑示例及解碼圖

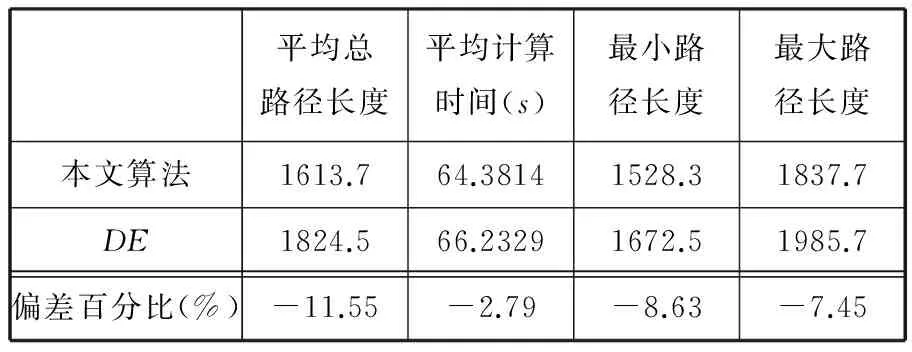
(3) 解的評價。一般情況下，對目標函數值進行比較可以評價可行解的優劣程度。因此本文選取目標函數值Z作為解的評價值。

2.2.2種群初始化

由于初始解質量對粒子群算法求解的速度和質量影響較大，本文采用大部分初始種群個體隨機生成、部分優良個體采用改進節約法[21]生成得到初始種群。隨機產生方法遵循以下兩條原則：第一，不允許產生相同的路徑，若隨機產生的路徑與已存在的初始種群中的粒子完全相同，則在一定代數內重新產生直至不相同為止；第二，隨機產生的路徑與已產生粒子的目標值之差應不小于某一數值Δ(通常Δ=2[17])。

改進節約法是在Clark和Wright的經典C-W節約法基礎上，綜合考慮車輛總行駛距離、時間窗、同時取送貨以及車輛容量限制等約束因素，重新定義節約值的算法。改進的節約值計算公式為[21]

(18)

(1)建立一條只包含物流中心0的大路徑X。

(2)將所有客戶按時間窗下限進行升序排列，命名為剩余客戶群。

(3)取出第一個客戶(即具有最小時間下限的客戶)作為當前客戶，將當前客戶插入大路徑X；同時將當前客戶從剩余客戶群中去除，得到新的剩余客戶群。

(4)按式(18)計算當前客戶與所有剩余客戶的新節約值，選取與當前客戶具有最大新節約值的客戶插入X；更新剩余客戶群，如果剩余客戶群不為空，轉步驟(3)，否則輸出大路徑X。

2.2.3位置更新準則

本文采用離散PSO策略實現個體粒子的位置更新。每次迭代時隨機生成變異概率u1、個體交叉概率u2和全局交叉概率u3。根據式(15)，當u1≤w時進行自身變異操作，否則不變異；當u2≤c1時與個體極值進行交叉操作，否則不交叉；當u3≤c2時與全局極值進行交叉操作，否則不交叉。

變異操作采用兩點插入式變異。任意選擇待變異粒子中的兩個位置(第一個位置除外)，將粒子中所選兩個位置之間的所有元素按原順序取出，作為變異粒子的前段，然后依次按原順序插入第一個位置前的所有元素、所選擇兩個位置上的元素、第二個位置之后的所有元素，便得到變異后的粒子序列。具體變異過程如圖2所示。

交叉操作采用PTL兩點交叉[15]。由于個體粒子可能與個體極值或全局極值的位置相同，PTL兩點交叉可以使相同序列交叉后得到不同的新序列。以個體粒子與個體極值交叉為例，PTL兩點交叉步驟為：任意選擇待交叉個體粒子中的兩個元素(第一個元素除外)，交叉時首先將個體極值中的對應兩個元素按原順序取出，作為交叉粒子的前段，然后從個體極值中依次選擇其他元素放置在其后，形成新的交叉粒子。具體交叉過程如圖3所示。

圖 2　粒子變異操作

圖 3　粒子交叉操作

2.2.4局域搜索

本文以車輛路徑問題中常用的六種鄰域機制為基礎，設計一種變鄰域下降搜索程序作為局域搜索方法，用于位置更新后個體粒子的深度搜索，尋求以較快的速度在更大搜索空間內優化個體搜索質量，并據此作為個體極值及全局極值的選擇依據。這六種鄰域機制為：

(1)路徑間部分交叉。對任意兩條子路徑，選擇不同的位置將每條子路徑分為前后兩部分，將后面兩部分進行交換得到兩條新的子路徑。對所有子路徑、所有可行的位置進行分段交叉，選擇令總配送成本最小的交叉結果作為新的個體。

(2)路徑間兩點交換。分別選擇兩條子路徑上的一個元素，從原路徑上刪除后，插入到另一條子路徑中。插入前，首先確定距離當前待插入元素最近的k個客戶，判斷另一條子路徑中是否至少存在k個客戶中的一個客戶，如果存在則選擇插入后新路徑總配送成本最小的位置，否則不插入。

(3)路徑間單點轉移。對任意兩條子路徑，選擇一條路徑上的一個元素并刪除后，將其插入到另一條子路徑中。對所有插入位置，選擇令插入后新路徑總成本最小的位置。

(4)路徑內部分逆轉，即為2-OPT操作。對任意一條子路徑選擇兩個位置，通過對兩個位置之間部分執行逆轉產生新的子路徑。對所有可行的位置對，選擇令操作后新路徑總成本最小的位置對。

(5)路徑內兩點交換。對任意一條子路徑選擇兩個位置并相互交換形成新的子路徑。對所有可行的位置對，選擇令操作后新路徑總成本最小的位置對。

(6)路徑逆轉。對任意一條子路徑，將原序列從后向前顛倒順序。該操作并不影響總的送貨量與總的取貨量，但可能降低車輛在不同客戶點的最大裝載量使其滿足車容量，或者改變車輛到達客戶的時間使其滿足客戶時間窗要求，從而為后續迭代過程中的新客戶插入提供機會。

上述鄰域機制中，前三種為路徑間操作，后三種為路徑內操作。由于路徑間操作使得個體變異幅度較大，路徑內操作的變異幅度較小，因此本文以有效變異為前提設計一種變鄰域下降搜索程序，基本搜索思想為：首先按上述鄰域機制順序執行鄰域搜索，如果搜索得到更好的目標值，則對該鄰域進行路徑內深度搜索，否則繼續按上述順序進行下一個鄰域機制搜索。詳細搜索步驟如下：

(1)設定搜索對象。設定搜索對象為大路徑X及其配送路徑集合R。

(2)按上述六種順序初始化鄰域機制編號，初始令o=1。

(3)對集合R，設當前域為h，如果o≤6，采用第o個鄰域機制尋找到當前域h的最好鄰域h′,轉步驟(4)；否則，轉步驟(5)。

(4)如果尋找到的鄰域目標值比當前目標值低，即f(h′)

(5)輸出新的配送路徑集合R和大路徑X。

由于客戶變動會影響車輛在路徑不同節點的最大裝載量及到達時間的變化，從而使得新路徑成為不可行路徑，因此每一次鄰域操作時都必須對路徑進行可行性檢查，即對各客戶點的最大裝載量及客戶時間窗、車輛返回物流中心的時間窗進行可行性判斷。為保障鄰域搜索的有效性，只有滿足可行性檢查的鄰域操作及相應更新才被接受。

2.2.5粒子“極值”更新方法

隨著迭代次數的增加，種群多樣性快速下降使得粒子過早收斂而陷入局部極值。解決該問題的常用辦法是采用模擬退火思想概率接受劣解，或者引入變異機制對停滯粒子進行變異。對粒子個體極值采用模擬退火思想接受劣解，接受準則為：計算粒子迭代后和迭代前解的變化量ΔE，若ΔE≤0，接受新值；若exp(-ΔE/T)>rand(0,1)，也接受新值；否則拒絕。其中，T表示退火溫度，rand(0,1)為0 ～ 1之間的隨機數。

若全局極值在若干代內未改進，則認為種群陷入局部最優位置。全局極值更新方法為：以一定比例選取種群中目標值最低的粒子進行兩點換位變異操作，若變異后粒子目標值小于全局極值，則更新全局極值，否則不更新。

2.2.6算法步驟

混合離散粒子群算法的具體步驟如下：

(1)初始化種群參數S、變異概率w、交叉概率c1和c2、局域搜索概率pL、最大迭代次數Imax、全局極值連續未更新最大次數Mg。

(3)判斷是否滿足終止條件。如果Ng>Mg且t>Imax則滿足終止條件，轉步驟(5);否則不滿足終止條件，轉步驟(4)。

(5)輸出全局極值粒子Xg、全局極值Cg以及最優配送方案。

3實驗結果與比較

為驗證算法尋優性能，選取2個算例進行尋優測試。算法采用MATLABR2009b編程語言實現。微機運行環境為：CPUi5-2520，主頻 2.5GHz，內存4G。

3.1算例選取及實驗參數設置

選取文獻[10]的算例2作為本文的算例1，用于驗證模型(1)中m= 0，n = 1的情況。該算例按一定規律生成客戶規模為40的VRPTWSPD問題相關數據，以車輛最大行駛距離作為物流中心的限制條件，要求有效安排行車路線使得車輛總行駛距離最短。

文獻[11]的VRPTWSPD算例基于Solomon經典的帶時間窗VRP算例集，但未給出客戶送貨量與取貨量的取值方法，故無法直接作為參考算例。RC1問題的客戶部分叢聚部分分散、客戶時間窗較窄，車輛行程較短、需求的車輛數量較多，是Solomon算例集中最復雜的一種情況。因此，本文分別選擇算例RC101、RC104、RC107的前10、25和50個客戶的基礎數據，產生9組新的VRPTWSPD算例集作為本文的算例2；9組新算例依次命名為RCdp10101、RCdp25101、RCdp50101、RCdp10104、RCdp25104、Cdp50104、RCdp10107、RCdp25107、RCdp50107。算例中基礎數據保持不變，客戶送貨量di及取貨量pi數據按如下規則生成：設原算例中客戶i需求量為Gi，客戶i的坐標為(xi,yi)，令ri=min(xi/yi,yi/xi)，則di=Giri，pi=Gi(1-ri)。此外,由于總配送成本最小化目標通過使用車輛數最少和車輛行駛距離最短兩個子目標實現，因此本例設車輛指派成本為一個很大的正整數，車輛單位距離行駛成本g = 1。算例2用于測試算法對模型(1)的求解精度，同時也用于分析種群初始化方法及局域搜索對算法性能的影響。

通過測試，參數設置為：種群S = 20，局域搜索概率pL=0.3，變異概率w = 0.4，交叉概率c1=c2=0.6;初始化種群參數α的取值范圍為[1.5, 3.5]，β的取值范圍為[0.1, 0.5]，γ的取值范圍為[0.5, 1.0]，λ的取值范圍為[0.5, 1.5]；粒子極值更新溫度參數T=30，q = 0.98。對算例1，設置最大迭代次數Imax= 500，全局極值連續未更新最大次數Mg= 100；對算例2，設置最大迭代次數Imax= 1500，全局極值連續未更新最大次數Mg= 200。

3.2仿真結果分析

3.2.1算例1分析

表 1　算例1分析結果

3.2.2算例2分析

以本文新產生的算例2為基礎數據，采用文獻[11]的聯合進化遺傳算法(GA)以及本文算法分別進行仿真計算，9組算例的計算結果對比分析如表2所示。表中加粗字體表示計算得到的最優值。可見，GA算法在客戶數為10、25的算例條件下，計算速度較快，且在RCdp25101算例中得到了好的決策結果，即使用車輛數為5、行駛距離為507.56km。本文算法在客戶數為50的算例條件下，具有更好的近似最優解，如在RCdp50101及RCdp50107算例中，盡管行駛距離比GA算法大一些，但使用車輛數較之少1輛。由于車輛指派成本為一個很大的正整數，因此車輛數目的減少可以大大降低總配送成本。由此可以推論，本文算法在求解VRPTWSPD問題時具有更好的尋優能力。

表2　算例2計算結果比較

為了進一步分析種群初始化方法及局域搜索對算法性能的影響，選取RCdp25101作為對比分析對象，以迭代500次為上限，獨立運算10次選取最優近似解進行分析。圖4給出了采用2.2.2節的種群初始化方法(INITIAL)與采用另一種初始化種群方法(NO_INITIAL)，以任意產生I條大路徑序列方式對種群進行初始化的算法收斂性對比。可見，在INITIAL情況下初始行駛距離較NO_INITIAL情況下初始行駛距離要小很多，收斂速度更快，最優行駛距離更小。這說明初始化種群方法對本文算法求解VRPTWSPD問題的性能具有較大影響，良好的種群初始化方法能促使其收斂加快并保持良好的尋優能力。

圖4　INITIAL與NO_INITIAL收斂性對比

圖5　LOCAL與NO_LOCAL情況下收斂性對比

圖5給出了采用2.2.4節的局域搜索方法(LOCAL)與不采用局域搜索方法(NO_LOCAL)時的對比情況。由圖5可見，在LOCAL情況下粒子收斂速度較快，迭代次數少且最小行駛距離更短。這說明本文提出的局域搜索在粒子群算法求解VRPTWSPD問題時，能大大減少迭代次數，縮短計算時間,有效避免陷入局部最優。

4結語

帶時間窗裝卸一體化車輛路徑問題是一類應用廣泛的復雜車輛路徑問題，因其決策目標、決策因素和限制條件較多等特征需要高求解性能的啟發式方法或元啟發算法。針對帶時間窗裝卸一體化車輛路徑問題，建立了隱含兩個子目標的混合整數規劃模型，提出了求解帶時間窗裝卸一體化車輛路徑問題的混合離散粒子群算法。該算法采用基于C-W的改進啟發式方法產生初始種群，在一定概率下對粒子進行局域搜索，并采用模擬退火思想接受粒子個體極值劣解。針對不同總目標，分別基于兩個算例進行仿真分析。仿真結果表明，無論是單純以總行駛距離為目標的算例1問題，還是以總配送成本為總目標、以車輛數最少和總行駛距離最短為子目標的算例2問題，本文提出的混合離散粒子群算法都能以較快的收斂速度找到近似最優解，且尋優性能好于已有的改進差分進化算法和聯合進化遺傳算法。由此可見，本文所提算法對于具有不同時間約束服務的物流配送和取貨優化問題具有重要的指導意義，同時對于離散型組合優化問題的進一步研究也具有一定的理論參考價值。

參考文獻：

[1]BerbegliaG,CordeauJF,GribkovskaiaI,etal.StaticPickupandDeliveryProblems:aClassificationSchemeandSurvey[J].TOP,2007,15(1):1-31.

[2]郎茂祥. 物流配送車輛調度問題的模型和算法研究[D]. 北京：北方交通大學, 2002.

[3]MinH.TheMultipleVehicleRoutingProblemwithSimultaneousDeliveryandPick-upPoints[J].TransportationResearchPartAGeneral, 1989, 23(5): 377-386.

[4]DethloffJ.VehicleRoutingandReverseLogistics:theVehicleRoutingProblemwithSimultaneousDeliveryandPick-up[J].OrSpectrum, 2001, 23(1): 79-96.

[5]BianchessiN,RighiniG.HeuristicAlgorithmsfortheVehicleRoutingProblemwithSimultaneousPick-upandDelivery[J].Computers&OperationsResearch,2007,34:578-594.

[6]李雪, 聶蘭順, 齊文艷,等. 基于近似動態規劃的動態車輛調度算法[J].中國機械工程,2015,26(5):682-688.

LiXue,NieLanshun,QiWenyan,etal.AnAlgorithmofDynamicVehicleSchedulingProblemBasedonApproximateDynamicProgramming[J].ChinaMechanicalEngineering, 2015, 26(5):682-688.

[7]AiTJ,KachitvichyanukulV.AParticleSwarmOptimizationfortheVehicleRoutingProblemwithSimultaneousPickupandDelivery[J].Computers&OperationsResearch,2009,36:1693-1702.

[8]GajpalY,AbadP.AnAntColonySystem(ACS)forVehicleRoutingProblemwithSimultaneousDeliveryandPickup[J].Computers&OperationsResearch, 2009,36:3215- 3223.

[9]AngelelliE,MansiniR.ABranch-and-priceAlgorithmforaSimultaneousPick-upandDeliveryProblem[C]//LectureNotesinEconomicsandMathematicalSystems.USA:Springer, 2002: 249-267.

[10]LaiMingyong,CaoErbao.AnImprovedDifferentialEvolutionAlgorithmforVehicleRoutingProblemwithSimultaneousPickupsandDeliveriesandTimeWindows[J].EngineeringApplicationsofArtificialIntelligence, 2010, 23:188-195.

[11]WangHF,ChenYY.AGeneticAlgorithmfortheSimultaneousDeliveryandPickupProblemswithTimeWindow[J].Computers&IndustrialEngineering, 2012, 62: 84-95.

[12]王超, 穆東. 基于模擬退火算法求解VRPSPDTW問題[J]. 系統仿真學報, 2014,11(6):2618-2623.

WangChao,MuDong.SolvingVRPSPDTWProblemUsingSimulatedAnnealingAlgorithm[J].JournalofSystemSimulation, 2014, 11(6):2618-2623.

[13]BoubahriL,AddoucheSA,MhamediAE.Multi-antColoniesAlgorithmsfortheVRPSPDTW[C]// 2011InternationalConferenceonCommunications,ComputingandControlApplications(CCCA).NewYork:IEEE,2011: 1-6.[14]邱晗光, 張旭梅. 基于改進粒子群算法的開放式定位-運輸路線問題研究[J]. 中國機械工程, 2006, 17(22): 2359-2361.

QiuHanguang,ZhangXumei.ResearchonOpenLocationRoutingProblemBasedonImprovedParticleSwarmOptimizationAlgorithm[J].ChinaMechanicalEngineering, 2006, 17(22): 2359-2361.

[15]PanQK,TasgetirenMF,LiangYC.ADiscreteParticleSwarmOptimizationAlgorithmfortheNo-waitFlowshopSchedulingProblem[J].Computers&OperationsResearch, 2008, 35: 2807-2839.

[16]郭文忠, 陳國龍, 陳振. 離散粒子群優化算法綜述[J]. 福州大學學報(自然科學版), 2011, 39(5): 631-638.

GuoWenzhong，ChenGuolong，ChenZhen.SurveyonDiscreteParticleSwarmOptimizationalgorithm[J].JournalofFuzhouUniversity(NaturalScienceEdition), 2011, 39(5): 631-638.

[17]PrinsC.ASimpleandEffectiveEvolutionaryAlgorithmfortheVehicleRoutingProblem[J].Computers&OperationsResearch, 2004, 31: 1985-2002.

[18]BeasleyJE.Route-firstCluster-secondMethodsforVehicleRouting[J].Omega, 1983, 11:403-408.

[19]DuhamelC,LacommeP,ProdhonC.AHybridEvolutionaryLocalSearchwithDepthFirstSearchSplitProcedurefortheHeterogeneousVehicleRoutingProblems[J].EngineeringApplicationsofArtificialIntelligence, 2012, 25: 345-358.

[20]DuhamelC,LacommeP,ProdhonC.EfficientFrameworksforGreedySplitandNewDepthFirstSearchSplitProceduresforRoutingProblems[J].Computers&OperationsResearch, 2011, 38: 723-739.

[21]莊英群. 應用禁忌搜索法于混合送收貨之車輛途程問題[D] .臺中:逢甲大學, 2003.

(編輯王艷麗)

AHybridDiscreteParticleSwarmOptimizationAlgorithmforVehicleRoutingProblemwithTimeWindowsandSimultaneousPickupandDelivery

ZhouRongShenWeileiLiuMingzhouZhaoHan

HefeiUniversityofTechnology,Hefei, 230009

Abstract：Considering the relative importance of dispatching cost of vehicles and travelling cost of routes, a mixed integer mathematical formulation of the vehicle routing problem with time windows and simultaneous pickup and delivery (VRPTWSPD) was established to make the total delivery cost, the number of vehicles and the travel cost minimize simultaneously. A hybrid discrete particle swarm optimization algorithm was proposed for solving VRPTWSPD. Solutions of algorithm were represented by an intuitive fragment-free giant tour of a permutation of all customers, and were decoded and evaluated by the revised depth first search split procedure. A variable neighborhood descent search procedure was carried out under a certain probability for individuals at each iteration, so that individuals could update with depth search in multi-neighborhood and with bread search in global exploration. The simulated annealing idea and mutating a selective portion of worst individuals were applied to improve the stagnation of the search. The feasibility and effectiveness of the proposed algorithm were verified by two instances with different goals.

Key words：vehicle routing problem with time window; simultaneous pickup and delivery; discrete particle swarm optimization; variable neighborhood descent search

收稿日期：2015-04-28

基金項目：國家自然科學基金資助項目(71071046)

中圖分類號：TP3

DOI：10.3969/j.issn.1004-132X.2016.04.013

作者簡介：周蓉， 女，1977年生。合肥工業大學機械與汽車工程學院講師。主要研究方向為資源調度、物流系統優化。發表論文10余篇。沈維蕾，女，1969年生。合肥工業大學機械與汽車工程學院副教授。劉明周，男，1968年生。合肥工業大學機械與汽車工程學院教授、博士研究生導師。趙韓，男，1957年生。合肥工業大學機械與汽車工程學院教授、博士研究生導師。