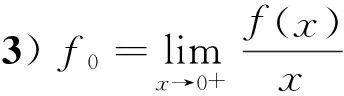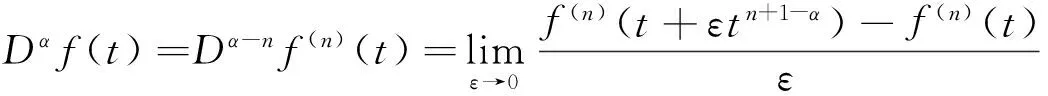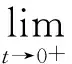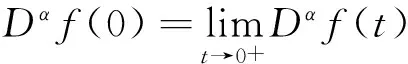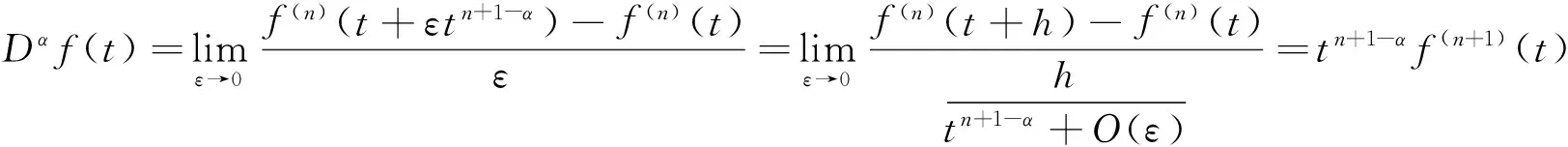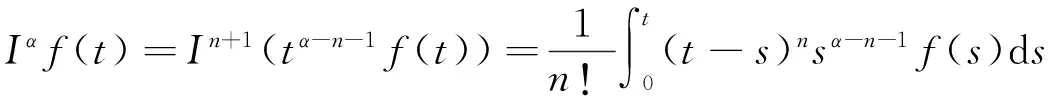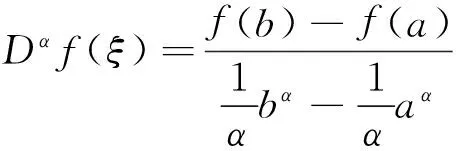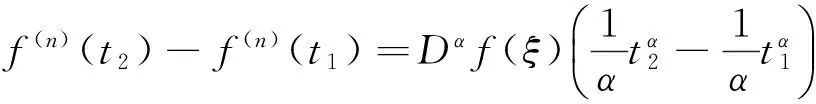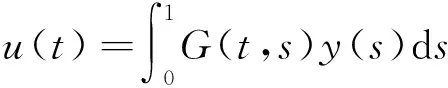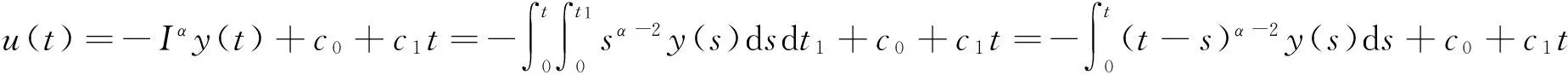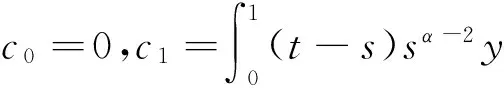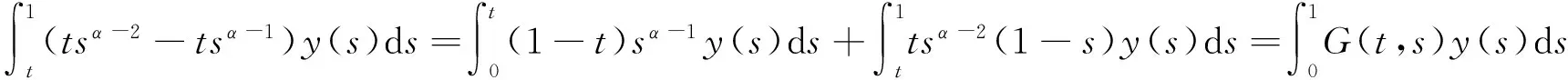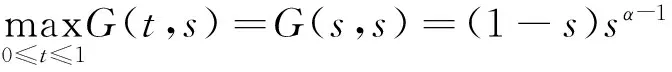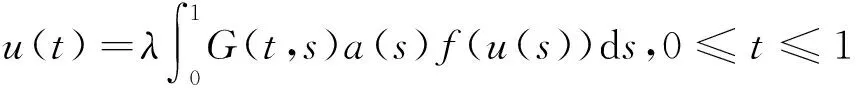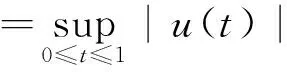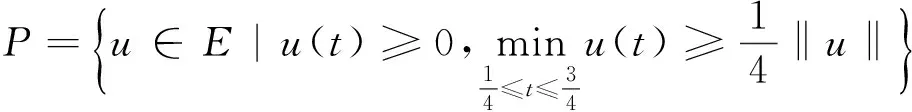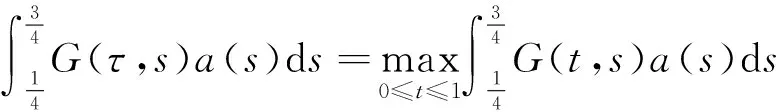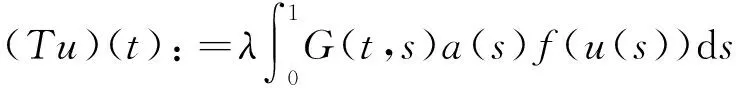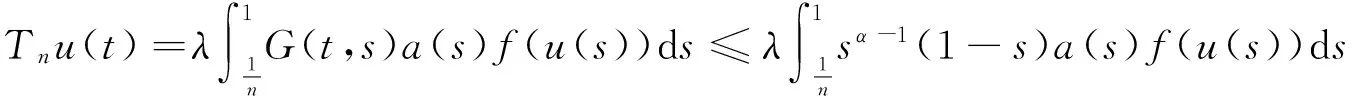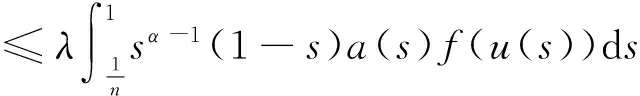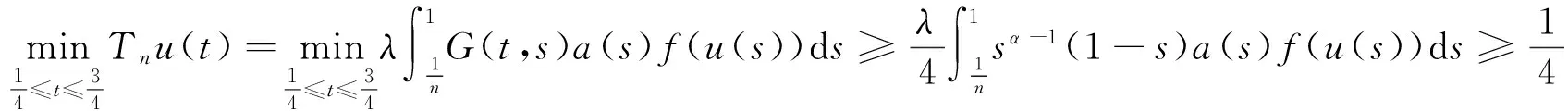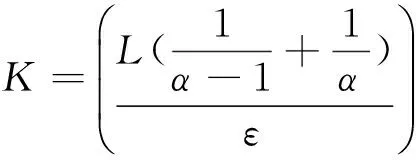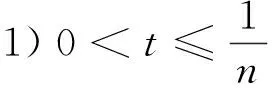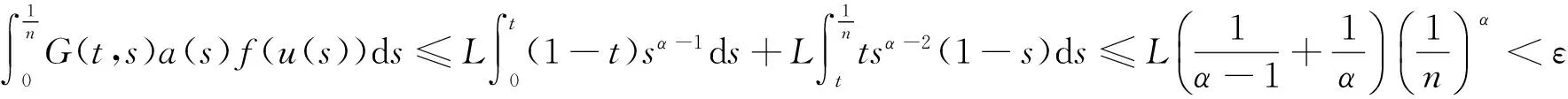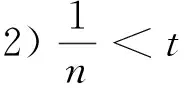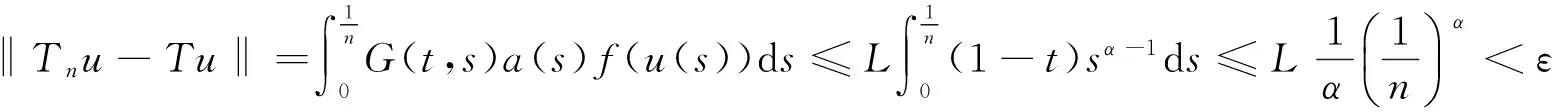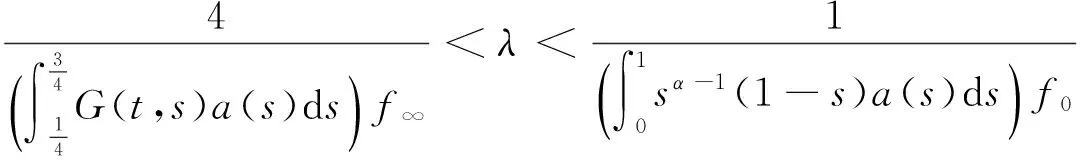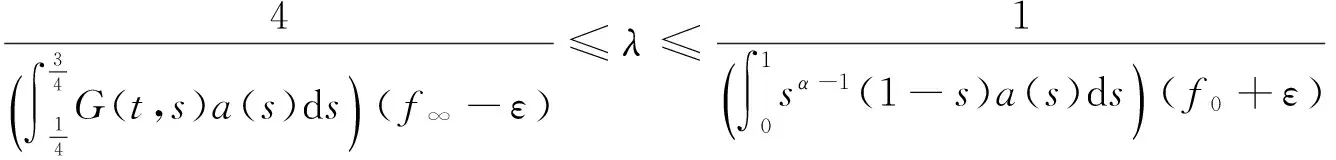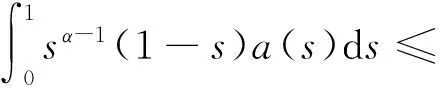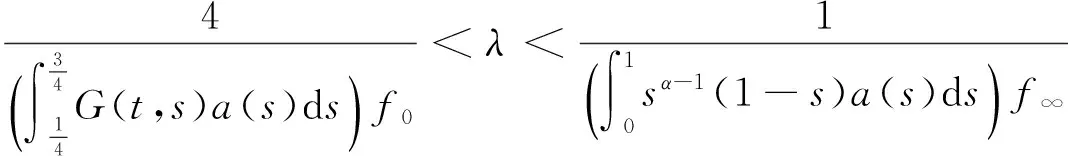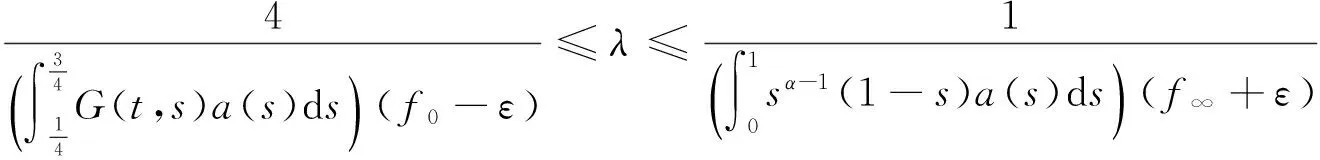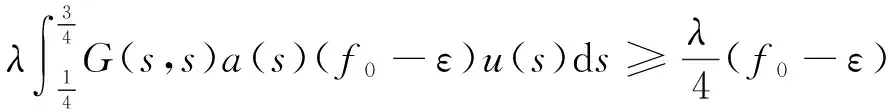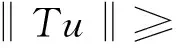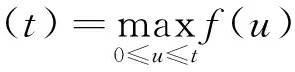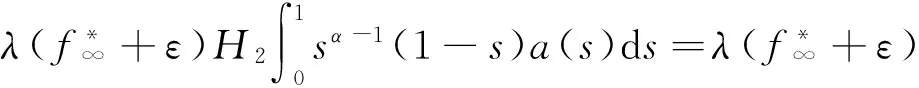具有適型分?jǐn)?shù)階導(dǎo)數(shù)的非線性特征值問題的正解
董曉玉,白占兵,張 偉
(山東科技大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,山東 青島 266590)
具有適型分?jǐn)?shù)階導(dǎo)數(shù)的非線性特征值問題的正解
董曉玉,白占兵,張偉
(山東科技大學(xué) 數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院,山東 青島 266590)
摘要:本文研究具有適型分?jǐn)?shù)階導(dǎo)數(shù)的非線性特征值問題正解的存在性。首先給出Green函數(shù)G(t,s)并且證明其非負(fù)標(biāo)和有界性;其次,利用Krasnosel’skii不動點(diǎn)定理對該問題的特征值區(qū)間給以刻劃,得到正解的存在性和多解性。
關(guān)鍵詞:適型分?jǐn)?shù)階導(dǎo)數(shù);非線性特征值問題;奇異Green函數(shù);Krasnosel’skii不動點(diǎn)定理
1引言
近年來,分?jǐn)?shù)階微積分和分?jǐn)?shù)階微分方程在眾多領(lǐng)域應(yīng)用廣泛,例如動力系統(tǒng)[1-2]、生物工程[3-4]、信號分析[5-6]、圖像處理[7]等。其中Henderson等[8]在1997年用Krasnosel′skill不動點(diǎn)定理研究了如下整數(shù)階的非線性特征值問題的正解:
u″(t)+λa(t)f(u)=0,0 u(0)=u(1)=0。 2012年Bai等[9]考慮了下列分?jǐn)?shù)階微分方程邊值問題: CDαu(t) + λh(t)f(u(t)) = 0,0 < t < 1, u(0)=u′(1)=u″(0)=0。 其中,2 基于此,本論文研究最近剛給出的適型分?jǐn)?shù)階導(dǎo)數(shù)的非線性特征值問題: Dαu(t)+λa(t)f(u(t))=0,0 (1) u(0)=u(1)=0。 (2) 其中,1 1) f:[0,1]×[0,∞)→[0,∞)是連續(xù)的, 2) a:[0,1]→[0,∞)連續(xù)且在任意子區(qū)間上不恒等0, 據(jù)我們了解,已有的關(guān)于邊值問題的文章[8-9,10,12]所涉及到的Green函數(shù)都是連續(xù)的,但本文所處理的問題其Green函數(shù)是奇異的。 本文結(jié)構(gòu)如下,第二部分給出適型分?jǐn)?shù)階導(dǎo)數(shù)的一些相關(guān)定義并且給出相應(yīng)的Green函數(shù);第三部分證明定義的積分算子是連續(xù)的,利用Krasnosel′skill不動點(diǎn)定理得到所考慮問題存在正解的特征值區(qū)間。 2預(yù)備知識 為了讀者的方便,此處給出一些微積分理論必要的定義。 定義 2.1[10]連續(xù)函數(shù)f:(0,∞)→R的α∈(n,n+1]階適型分?jǐn)?shù)階導(dǎo)數(shù)定義為 (3) (4) 注 2.1給定α∈(n,n+1],有 Dαtk=0, 其中k=0,1,…,n。 引理2.1設(shè)t>0,α∈(n,n+1]。函數(shù)f(t)是(n+1)階可微函數(shù)當(dāng)且僅當(dāng)f是α階可微的,并且 Dαf(t)=tn+1-αf(n+1)(t)。 證明設(shè)h=εtn+1-α+O(ε2),根據(jù)定義2.1,有 證畢。 定義2.2[9]連續(xù)函數(shù)f:(0,∞)→R的α∈(n,n+1]分?jǐn)?shù)積分定義為 (5) 其中In+1是n+1階積分算子。 引理2.2設(shè)α∈(n,n+1]。f在Iα的定義域下是一個連續(xù)函數(shù),t≥0時(shí)DαIαf(t)=f(t)。 證明因?yàn)閒(t)是連續(xù)的,那么Iαf(t)是(n+1)階可微的。由引理2.1有 tn+1-αf(t)tα-n-1=f(t)。 證畢。 引理2.3[9](中值定理)設(shè)a≥0,f:[a,b]→R具有以下性質(zhì) 1)f在[a,b]上是連續(xù)的, 2) 對于α∈(0,1),f在(a,b)上是α階可微的, 引理2.4設(shè)α∈(n,n+1],t>0時(shí),f是一個α階可微函數(shù),那么Dαf(t)=0,t∈[0,1],當(dāng)且僅當(dāng)f(t)=a0+a1t+…+an-1tn-1+antn,其中ak∈R,k=0,1,…,n。 證明充分性由注2.1可證。 接下來,給定t1,t2∈[0,1],t1 由Dαf(ξ)=0可知,f(n)(t2)=f(n)(t1),又由t1,t2的任意性,有f(t)=a0+a1t+…+an-1tn-1+antn,t∈[0,1]。證畢。 根據(jù)引理2.2和引理2.4,立即有下述引理。 引理2.5設(shè)α∈(n,n+1],u∈C(0,1)∩L(0,1)具有α階分?jǐn)?shù)導(dǎo)數(shù)并屬于C(0,1)∩L(0,1)。那么 IαDαu(t)=u(t)+c0+c1t+…+cntn, (6) 其中,ck∈R,k=0,1,…,n。 在以下的討論中,假設(shè)α∈(1,2]。 下面給出線性分?jǐn)?shù)階微分方程邊值問題的Green函數(shù)。 引理 2.6假設(shè)y∈C[0,1],則問題 Dαu(t)+y(t)=0,0 (7) u(0)=u(1)=0, (8) 的唯一解是 其中 (9) 證明:利用引理2.5可推出方程(7)等價(jià)于積分方程 證畢。 顯然α=2時(shí),式(9)即是通常的Green函數(shù)。 引理2.7由式(9)定義的Green函數(shù)G(t,s)滿足以下性質(zhì): 1)G(t,s)>0,對任意的t,s∈(0,1); 證明:由G(t,s)的表達(dá)式可知,G(t,s)>0,對t,s∈(0,1)成立。下面,對給定的s∈(0,1)可求出G(t,s)關(guān)于t的偏導(dǎo)數(shù), 由此可知G(t,s)關(guān)于t在s≤t時(shí)是遞減的,t≤s時(shí)是遞增的。 因此, 且 設(shè) 此處Green函數(shù)有一個常數(shù)界,這在Riemann-Liouville導(dǎo)數(shù)下是無法做到的[11]。 1)‖Ax‖≤‖x‖,x∈P∩?Ω1,且‖Ax‖≥‖x‖,x∈P∩?Ω2,或 2)‖Ax‖≥‖x‖,x∈P∩?Ω1,且‖Ax‖≤‖x‖,x∈P∩?Ω2 3主要結(jié)果 本文考查特征值問題(1),(2)的可解性。由引理2.6知u(t)是問題(1),(2)的解,當(dāng)且僅當(dāng) 設(shè)常數(shù)τ∈[0,1],定義如下 定義積分算子T,Tn:P→E為 引理3.1T:P→P是全連續(xù)算子。 證明:首先,證明Tn,n=3,4,…是一列全連續(xù)算子。由引理2.7,a(s)和f(u)的非負(fù)性可知,對于任意的t∈[0,1],u∈P,Tnu(t)≥0,且 所以, (11) 對u∈P,由引理2.7和(11)式得 因此,Tn是保錐映射。另外,標(biāo)準(zhǔn)的討論得Tn:P→P全連續(xù)。 顯然T:P→P。接下來證Tn:P→P一致收斂于T,從而T:P→P也是全連續(xù)算子。 任意的ε>0,令 則當(dāng)n>K時(shí),有‖Tnu-Tu‖<ε。分兩種情況考慮: 由引理2.8,T:P→P全連續(xù)。證畢。 定理3.1假設(shè)條件(A),(B)和(C)都滿足。那么,只要λ滿足 (12) 邊值問題(1),(2)至少有一個解。 證明:設(shè)λ是(12)式中給定的。選取ε>0使得 由引理3.1知,T:P→P是全連續(xù)算子。對上述ε>0,由f0的定義知,存在H1>0,使得f(x)≤(f0+ε)x,0 Ω1:={u∈P|‖u‖ 對于u∈?Ω1,0 因此,u∈P∩?Ω1時(shí)‖Tu‖≤‖u‖。 Ω2:={u∈P|‖u‖ 因此,u∈P∩?Ω2時(shí)‖Tu‖≥‖u‖。 定理 3.2假設(shè)條件(A),(B)和(C)都滿足。且 (13) 則邊值問題(1),(2)至少有一個解。 證明:設(shè)λ是(13)式中給定的。選取ε>0使得 Ω1:={u∈P|‖u‖ 有 Ω2:={u∈P|‖u‖ 如果u∈P∩?Ω2,有 參考文獻(xiàn): [1]MERALF,ROYSTONT,MAGINR.Fractionalcalculusinviscoelasticity,Anexperimentalstudy[J].CommunicationsinNonlinearScienceandNumericalSimulation,2010,15(14):939-945. [2]武華華,孫蘇菁.基于變分方法的四階邊值問題的多重正解[J].山東科技大學(xué)學(xué)報(bào)(自然科學(xué)版),2014,33(2):96-99. WUHuahua,SUNSujing.Basedonthevariationalmethodofthemultiplepositivesolutionsoffourth-orderboundaryvalueproblem[J].JournalofShandongUniversityofScienceandTechnology(NaturalScience),2014,33(2):96-99. [3]OLDHAMK,SPANIERJ.Thefractionalcalculus[M].NewYork:AcademicPress,1974:27-36. [4]PODLUBNYI.Fractionaldifferentialequations[M].NewYork:AcademicPress,1999:50-65. [5]KILBASA,SRIVASTAVAH,TRUJILLOJ.Theoryandapplicationsoffractionaldifferentialequations[M].Amsterdam,ElsevierScienceB.V.,2006:78-84. [6]WEITZNERH,ZASLAVSKYG.Someapplicationsoffractionalequations[J].CommunicationsinNonlinearScienceandNumericalSimulation,2003,8(3/4):273-281. [7]MACHADOJ,KIRYAKOVAV,MAINARDIF.Recenthistoryoffractionalcalculus[J].CommunicationsinNonlinearScienceandNumericalSimulation,2011,16(3):1140-1153. [8]HENDERSONJ,WANGH.Positivesolutionsfornonlineareigenvalueproblems[J].JournalofMathematicalAnalysisandApplications,1997,208(1):252-259. [9]BAIZ.Eigenvalueintervalsforaclassoffractionalboundaryvalueproblem[J].Computers&MathematicswithApplications2012,64(10):3253-3257. [10]LIUZ,LIF.MultiplePositivesolutionsofnonlineartwo-pointboundaryvalueproblem[J].JournalofMathematicalAnalysisandApplications,1996,203(3):610-625. [11]KHALILR,HORANIM,YOUSEFAandSABABHEHM.Anewdefinitionoffractionalderivative[J].JournalofComputationalandAppliedMathematics,2014,264(5):65-70. [12]BAIZ,LVH.Positivesolutionsofboundaryvalueproblemsofnonlinearfractionaldifferentialequation[J].JournalofMathematicalAnalysisandApplications,2005,311(4):495-505. [13]郭大鈞.非線性泛函分析[M].2版.濟(jì)南:山東科學(xué)技術(shù)出版社,2001:21-22. (責(zé)任編輯:傅游) Positive Solutions for Nonlinear Eigenvalue Problems with Conformable Fractional Differential Derivatives DONG Xiaoyu, BAI Zhanbing, ZHANG Wei (College of Mathematics and Systems Science, Shandong University of Science and Technology,Qingdao, Shandong 266590, China) Abstract:This paper established the existence of positive solutions for nonlinear eigenvalue problems with conformable fractional differential derivatives Firstly, Green's function was given and its properties were proved. Secondly, by using Krasnosel'skii fixed-point theorems, the interval of eigenvalue problems was investigated and its existence and multiplicity of positive solutions were acquired. Key words:conformable fractional derivative; nonlinear eigenvalue problems; singular Green′s function; Krasnosel′skii fixed point theorem 收稿日期:2016-01-06 基金項(xiàng)目:國家自然科學(xué)基金項(xiàng)目(11571207) 作者簡介:董曉玉(1992—),女,山東青島人,碩士研究生,主要從事分?jǐn)?shù)階微分方程的研究. 白占兵(1971—),男,甘肅高臺人,教授,博士,主要從事應(yīng)用微分方程的研究,本文通信作者. E-mail:zhanbingbai@163.com 中圖分類號:O175.1 文獻(xiàn)標(biāo)志碼:A 文章編號:1672-3767(2016)03-0085-07