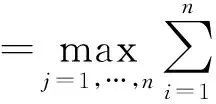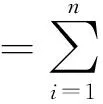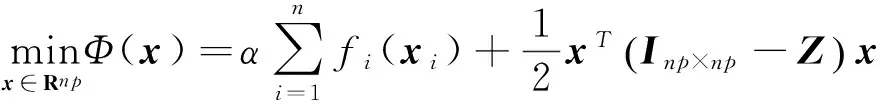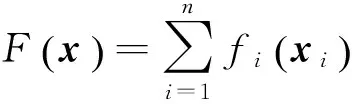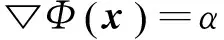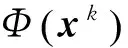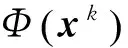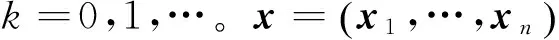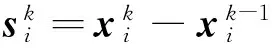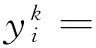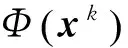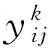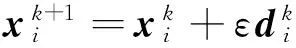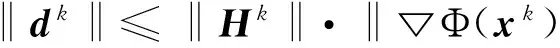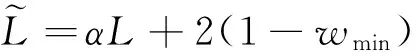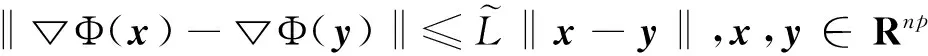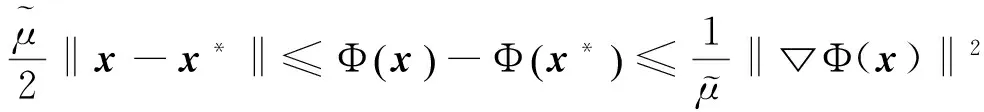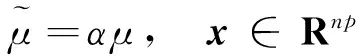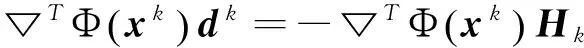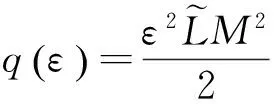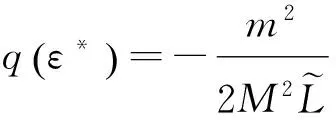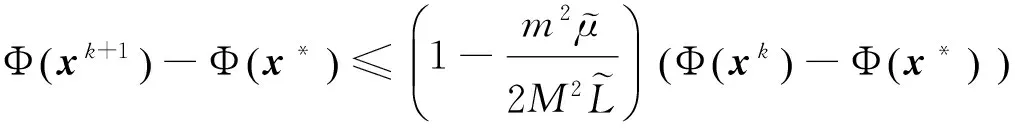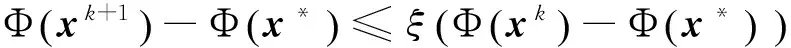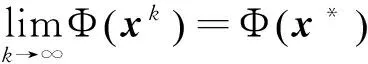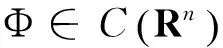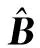求解無約束一致性優化問題的分布式擬牛頓算法

于慧慧，王永麗,陳勇勇，周秀娟

(1.山東科技大學 數學與系統科學學院，山東 青島 266590;2.山東科技大學 信息科學與工程學院，山東 青島 266590)

求解無約束一致性優化問題的分布式擬牛頓算法

于慧慧1，王永麗1,陳勇勇1，周秀娟2

(1.山東科技大學 數學與系統科學學院，山東 青島 266590;2.山東科技大學 信息科學與工程學院，山東 青島 266590)

摘要:本文主要針對網絡中各個節點相互協作，最大限度地使本地費用函數的總和最小的無約束一致性優化問題，提出了一類分布式擬牛頓算法。算法僅利用了目標函數的一階導數信息，每步通過選取一個滿足擬牛頓方程的正定對角矩陣來作為費用函數Hesse矩陣逆的校正矩陣，克服了校正矩陣的非稀疏性對算法分布式實現造成的困難，減少了計算量和存儲空間。在適當條件下，證明了分布式擬牛頓算法的全局收斂性及局部線性收斂速度，并通過數值實驗驗證了算法的優越性。

關鍵詞:無約束; 一致性優化; 分布式擬牛頓算法； 全局收斂; 線性收斂

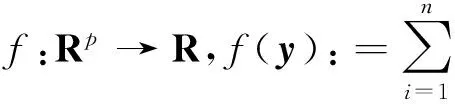
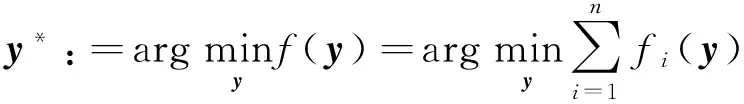
(1)

其中y*表示問題(1)的最優解。在現實生活中，這種形式的問題有很多，例如，大數據分析[1],分布式傳感器網絡[ 2-5 ]和分布式控制[6]等。

求解問題(1)的分布式方法分為兩類，一類是基于費用函數一階信息的方法，該類方法中研究較多的是分布式梯度法[7-10]，分布式交替方向乘子法[11-13]和分布式對偶平均法[14-15]。雖然這些算法之間存在著很大的差異，但基本思想都可以歸結為先進行本地下降步，然后與相鄰節點進行變量交換和信息整合。由于該類計算僅涉及到一階信息，導致了對下降方向曲率估計的不準確性，便得收斂速度較慢。另一類分布式方法是基于費用函數二階信息的方法，即分布式牛頓類算法，主要的文獻有[16-17]等。目前，對分布式牛頓類算法的研究較少，這主要是因為牛頓法的分布式實現比較困難且計算目標函數的二階信息計算量較大。但考慮到牛頓類算法比大多數一階方法具有更快的收斂速度，越來越多的學者開始了對該類算法的研究。

本文研究分布式求解問題(1)的擬牛頓方法，只需計算目標函數的一階信息，通過選取一個滿足擬牛頓方程的正定對角矩陣來作為費用函數Hesse矩陣逆的校正矩陣，來克服校正矩陣的非稀疏性對算法分布式實現造成的困難，從而實現擬牛頓法的分布式計算，減少計算量和存儲空間。同時，在適當條件下證明分布式擬牛頓算法的收斂性，并通過數值試驗驗證算法的有效性。應當指出的是，這里的分布式是指每個節點僅知道其本地費用函數，且只能夠與相鄰節點進行信息交換。

1預備知識

首先給出關于問題(1)的一些預備知識。

假設1假設函數fi:Rp→R是系數為μ>0的強凸函數，即

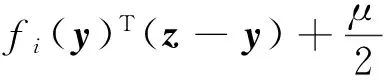
(2)

并且具有常數為L的Lipschitz連續梯度，即

‖▽fi(y)-▽fi(z)‖≤L‖y-z‖。

(3)

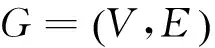
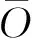
假設3矩陣W=WT∈Rn×n是元素為wij的隨機矩陣, 其中wij的定義如下：

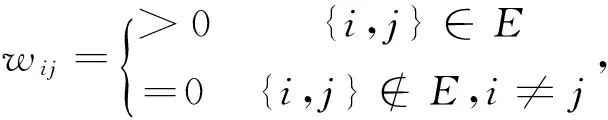
且存在常數wmin,wmax使得

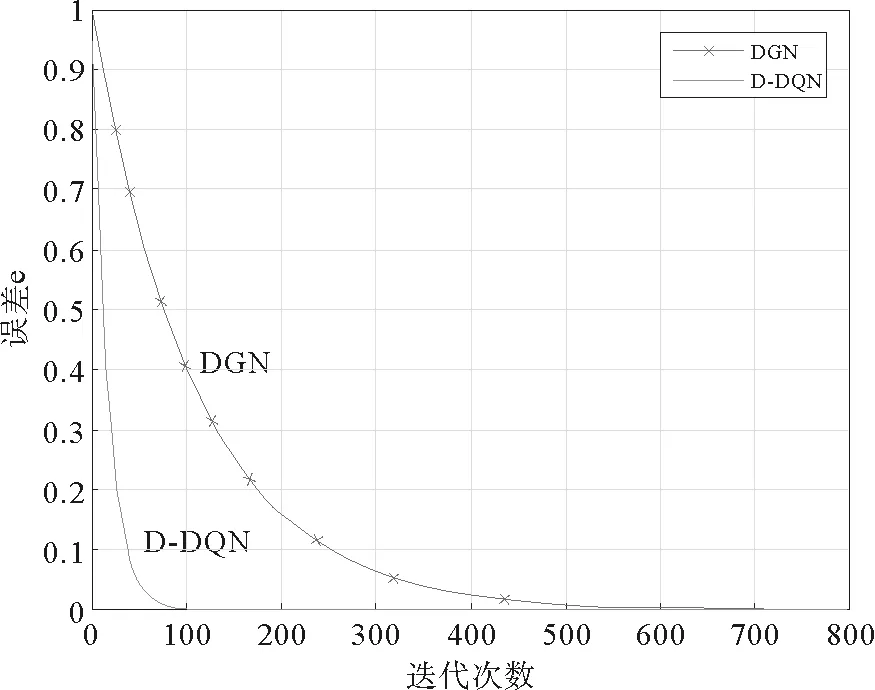
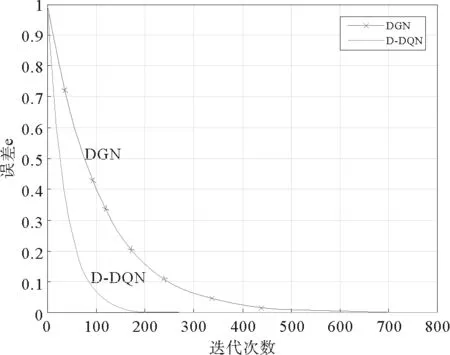
0

定義1[16]對于矩陣M=(Mij)∈Rnp×np，其中Mij∈Rp×p，定義M的范數如下：

類似的，對向量x∈Rnp，xi∈Rp，定義：

其中‖·‖2為歐式范數。

2分布式擬牛頓法

牛頓法的基本思想是利用目標函數的二次Taylor展開來逼近目標函數，但在實際問題中，尤其是大規模的高維問題中，如果所基于的網絡是稀疏的，則目標函數的二階導也可能是稀疏的，從而使得所求解的問題具有特殊結構。但遺憾的是，即使目標函數的Hesse矩陣是稀疏的，但其逆卻是稠密的。為了減少計算量，避免Hesse矩陣逆的計算，我們利用目標函數及其一階導數信息來近似Hesse矩陣的逆矩陣，通過構造特殊的擬牛頓矩陣，實現擬牛頓矩陣的分布式計算。

2.1問題的等價變形

引入輔助函數Φ:Rnp→R，令x=(x1,…,xn)∈Rnp，并記Z∈Rnp×np為W和單位矩陣I∈Rp×p的Kronecker積：Z=W?I，則由文獻[18]可知問題(1)等價于如下問題：

(4)

其中α>0 為罰參數，Inp×np表示np×np的單位矩陣。

(5)

2.2算法框架

求解問題(4)的擬牛頓法的基本迭代格式為：xk+1=xk+εdk。

(6)

(7)

Hk是目標函數Hesse矩陣逆矩陣的近似，滿足正定性和如下擬牛頓條件：

Hkyk=sk。

(8)

(9)

其中hij表示對角矩陣hi的第j個對角元，yij表示子向量yi中第j個分量，sij表示子向量si的第j個分量。

(10)

(11)

于是，由(7)式可以寫出在每個節點i處的下降方向：

(12)

(13)

由上述討論可得分布式擬牛頓算法(Distributed-DiagonalQuasi-Newton,D-DQN)的框架如下：

分布式擬牛頓算法 對每個節點i,給定α,ε>0。步1.初始化:對每個節點i,令k=0,給定初始點x0i,x1i∈Rp。步2.對每個節點i,將其迭代點xki傳遞給其相鄰節點j∈Oi,并從相鄰節點接收xkj.步3.對每個節點i,計算搜索方向:dki=-hkiα▽fixki()+∑j∈Oiwijxki-xkj()[]步4.對每個節點i,更新其近似解:xk+1i=xki+εdki步5.由(10)式、(11)式計算hk+1i的元素,令k=k+1,返回步2.

注：注意到擬牛頓方法每步迭代都涉及到當前節點及其相鄰節點前兩步的變量信息，因此在給定初始條件時，每個節點需要給出兩個初始值。在算法的第2步，每個節點需要與其相鄰節點進行信息交換。 第3步中計算搜索方向時涉及到了參數α，這一參數的取值在文獻[18]中已有研究，本文在數值實驗時取α為固定值。算法第4步，本文采用一個固定步長ε，顯然變量的迭代只涉及到自身的函數信息和相鄰節點的信息，實現了問題(1)的分布式計算。

3收斂性分析

引理1若假設1～3成立，則有‖dk‖≤M‖▽Φ(xk)‖。

證明因為Hk為塊對角矩陣，由本文中范數的定義，可知：

因此，由dk的定義可得

(14)

(15)

(16)

證明由算法的迭代過程與題設可得

于是，由引理1可得

(17)

(18)

4數值實驗

本節通過數值實驗來驗證D-DQN算法求解問題(1)的有效性，并將本文提出的算法與分布式梯度法(DGN)在迭代次數和運行時間兩方面進行比較。實驗運行環境為Pentium(R)E5500 2.77GHz雙核處理器，內存2.00GB。所有算法程序均用Matlab2015a編寫。

實驗生成節點個數為n的連通網絡，考慮如下形式一致性問題

當全局變量維數p=3，圖1、圖2分別取不同網絡節點數時，分布式梯度下降法(DGN)和分布式擬牛頓算法(D-DQN)迭代次數與誤差的關系曲線。可以看出，分布式擬牛頓算法的收斂速度要快于分布式梯度下降方法，且在剛開始迭代時表現出非常快的下降速度，從而體現出分布式擬牛頓法在求解大規模稀疏一致性優化問題中的優越性。

圖1　當n=100時，D-DQN算法與DGN算法的比較

圖2　當n=200時，D-DQN算法與DGN算法的比較

5結論

本文針對無約束一致性優化問題(1)，提出了一類新的分布式擬牛頓算法，算法通過選取一個近似滿足擬牛頓方程的正定對角矩陣來近似費用函數Hesse矩陣的逆，實現了擬牛頓算法的分布式實現。在取固定步長的情況下，證明了算法的全局收斂性及局部線性收斂速度，并通過數值實驗驗證了算法的有效性。實驗結果表明，分布式擬牛頓算法在求解大規模稀疏一致性優化問題方面具有較好的應用前景。

參考文獻：

[1]DANESHMAND A,FACCHINEI F,KUNGURTSEV V,et al. Hybrid random/deterministic parallel algorithms for nonconvex big data optimization[J].Journal of Inverstigative Medicine，2014，60(4)：671-675.

[2]SCHIZAS I D,RIBEIRO A,GIANNAKIS G B.Consensus in ad hoc WSNs with noisy links—Part I:Distributed estimation of deterministic signals[J].IEEE Transactions on Signal Processing,2008,56(1):350-364.

[3]KAR S,MOURA J M F,RAMANAN K.Distributed parameter estimation in sensor networks:Nonlinear observation models and imperfect communication[J].IEEE Transactions on Information Theory,2012,58(6):3575-3605.

[4]SAYED A H,LOPES C G.Adaptive Processing over distributed networks[J].Leice Transactions on Fundamentals of Electronics Communications and Computer Sciences,2007,E90-A(8):1504-1510.

[5]CATTIVELLI F S,SAYED A H.Diffusion LMS strategies for distributed estimation[J].IEEE Transactions on Signal Processing,2010,58(3):1035-1048.

[6]MOTA J F C,XAVIER J M F,AGUIAR P M Q,et al.Distributed optimization with local domains:Applications in MPC and network flows[J].IEEE Transactions on Automatic Control，2015,60(7):2004-2009.

[8]JAKOVETIC D,XAVIER J,MOURA J M F.Fast distributed gradient methods[J].IEEE Transactions on Automatic Control,2014,59(5):1131-1146.

[9]YUAN K,LING Q,YIN W.On the convergence of decentralized gradient descent[DB/OL].(2015-07-01)[2016-01-05].http://arXiv preprint arXiv:1310.7063.

[10]SHI W,LING Q,WU G,et al.Extra:An exact first-order algorithm for decentralized consensus optimization[J].SIAM Journal on Optimization,2015,25(2):944-966.

[11]LING Q,RIBEIRO A.Decentralized linearized alternating direction method of multipliers[C]//IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP),2014:5447-5451.

[12]BOYD S,PARIKH N,CHU E,et al.Distributed optimization and statistical learning via the alternating direction method of multipliers[J].Foundations and Trends in Machine Learning,2011,3(1):1-122.

[13]SHI W,LING Q,YUAN K,et al.On the linear convergence of the ADMM in decentralized consensus optimization[J].IEEE Transactions on Signal Processing,2014,62(7):1750-1761.

[14]DUCHI J C,AGARWAL A,WAINWRIGHT M J.Dual averaging for distributed optimization:convergence analysis and network scaling[J].IEEE Transactions on Automatic control,2012,57(3):592-606.

[15]TSIANOS K I,LAWLOR S,RABBAT M G.Push-sum distributed dual averaging for convex optimization[C]//IEEE 51st Annual Conference on Decision and Control (CDC),2012:5453-5458.

[16]BAJOVIC D,JAKOVETIC D,KREJIC N,et al.Newton-like method with diagonal correction for distributed optimization[DB/OL](2015-09-05)[2016-01-05].http：//arXiv preprint arXiv:1509.01703.

[17]MOKHTARI A,LING Q,RIBEIRO A.An approximate Newton method for distributed optimization[C]//IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP), 2015.

[18]JAKOVETIC D,MOURA J M F,XAVIER J.Distributed Nesterov-like gradient algorithms[C]//IEEE 51st Annual Conference on Decision and Control (CDC),2012:5459-5464.

[19]時貞軍,孫國.無約束優化問題的對角稀疏擬牛頓法[J].系統科學與數學,2006,26(1):101-112.

SHI Zhenjun,SUN Guo.A diagonal-sparse quasi-Newton method for unconstrained optimization problem[J].Journal of Systems Science and Mathematical Sciences,2006,26(1):101-112.

(責任編輯：傅游)

Distributed Quasi-Newton Algorithm for Solving Unconstrained Consensus Optimization

YU Huihui1, WANG Yongli1, CHEN Yongyong1, ZHOU Xiujuan2

(1. College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao Shandong 266590, China;2. College of Information Science and Engineering, Shandong University of Science and Technology,Qingdao, Shandong 266590, China)

Abstract:A class of distributed quasi-Newton algorithm was proposed for solving the unconstrained consensus optimization, where the network nodes work collaboratively to minimize the sum of their locally known convex costs. The new algorithm used only the first-order derivative information of the cost function. By choosing a positive definite diagonal matrix as the quasi-Newton correction of the inverse of the Hesse matrix of the cost function at each iteration, the proposed algorithm successfully overcame the difficulty caused by the non-sparsity of the correction matrix in the implementation of distribution, and greatly decreased computation and storage pressure. Under suitable conditions, the proposed distributed quasi-Newton algorithm was proved to be globally convergent with local linear convergence rate and its superiority was verified by numerical simulations.

Key words:unconstrained consensus optimization; distributed quasi-Newton algorithm; global convergence; linear convergence

收稿日期：2016-01-05

作者簡介：于慧慧(1991—)，女，山東菏澤人，碩士研究生，主要從事分布式優化算法的研究.E-mail：yxh622@163.com 王永麗(1977—)，女，山東棲霞人，博士，副教授，主要從事非線性優化理論與算法、分布式優化算法、并行計算的研究，本文通信作者.E-mail：wangyongli@sdkd.net.cn

中圖分類號：O224

文獻標志碼：A

文章編號：1672-3767(2016)03-0112-07