Laguerre函數(shù)在時(shí)域匹配邊界元中的應(yīng)用研究

李志富，任慧龍，石玉云，李輝

(哈爾濱工程大學(xué) 船舶工程學(xué)院，黑龍江 哈爾濱 150001)

Laguerre函數(shù)在時(shí)域匹配邊界元中的應(yīng)用研究

李志富，任慧龍，石玉云，李輝

(哈爾濱工程大學(xué) 船舶工程學(xué)院，黑龍江 哈爾濱 150001)

摘要：利用滿足自由表面條件的時(shí)域格林函數(shù)求解波浪與浮體相互作用問題時(shí)，對于外飄型浮體計(jì)算結(jié)果時(shí)常發(fā)散。針對此問題，建立了內(nèi)外場時(shí)域快速匹配邊界元模型，通過與解析解對比，驗(yàn)證了數(shù)值模型的有效性。其次，利用所建立的匹配邊界元模型，研究了流場記憶速度勢隨時(shí)間的變化特點(diǎn)。針對長時(shí)間模擬，時(shí)間卷積積分項(xiàng)導(dǎo)致模擬失敗問題，提出了利用Laguerre函數(shù)對記憶速度勢時(shí)間變量進(jìn)行級數(shù)逼近，以對時(shí)間卷積積分進(jìn)行解析計(jì)算，并對級數(shù)收斂速度進(jìn)行了研究。最后，為加快級數(shù)收斂速度，引入了放縮系數(shù)，并對其特性進(jìn)行了探討。數(shù)值結(jié)果表明，通過引入放縮系數(shù)，可以利用較少的級數(shù)項(xiàng)來逼近速度勢的時(shí)間變量，能夠很好地描述記憶速度勢的脈沖特性。

關(guān)鍵詞：Laguerre函數(shù)；時(shí)域匹配；時(shí)間卷積；多項(xiàng)式逼近；放縮系數(shù)

網(wǎng)絡(luò)出版地址：http://www.cnki.net/kcms/detail/23.1390.U.20160411.0845.014.html

波浪與浮體相互作用的時(shí)域模擬具有重要意義[1]。在勢流理論框架下，根據(jù)所選取格林函數(shù)的不同，主要分為時(shí)域Rankine源法和時(shí)域自由面格林函數(shù)法。對于時(shí)域自由面格林函數(shù)法，只需要在船體表面進(jìn)行積分，國內(nèi)外許多學(xué)者都在此方面做了研究[2-3]。此方法對于不同浮體進(jìn)行模擬時(shí)，都需要重新計(jì)算時(shí)域格林函數(shù)在每一時(shí)刻的值，而時(shí)域格林函數(shù)的計(jì)算又需要占用較長的CPU時(shí)間，所以該方法計(jì)算效率較低。此外，格林函數(shù)在近水面單元的高頻振蕩特性[4]，導(dǎo)致外飄型船舶的計(jì)算，結(jié)果時(shí)常發(fā)散。對于時(shí)域Rankine源法，其形式簡單，且易與高階邊界元法相結(jié)合，以進(jìn)行非線性問題的模擬，所以現(xiàn)在仍然有很多學(xué)者對此進(jìn)行研究[5-6]。但是，時(shí)域Rankine法需要對計(jì)算域進(jìn)行截?cái)啵倚枰贾孟鄳?yīng)的人工遠(yuǎn)方輻射條件。

通過對時(shí)域Rankine源法和時(shí)域自由面格林函數(shù)法各自優(yōu)缺點(diǎn)的分析，有學(xué)者提出了匹配方法[7-8]，此種方法不僅避免了不同浮體都需對格林函數(shù)進(jìn)行計(jì)算的問題，同時(shí)適用于外飄型船舶的計(jì)算。但是此方法的準(zhǔn)確性和有效性仍需進(jìn)一步驗(yàn)證。無論是時(shí)域Rankine源法還是匹配方法，在計(jì)算與時(shí)間相關(guān)的記憶速度勢時(shí)，時(shí)間卷積項(xiàng)的存在，常常導(dǎo)致長時(shí)間的模擬無法進(jìn)行。

針對上述問題，本文首先建立了三維內(nèi)外場時(shí)域快速匹配邊界元模型，通過與解析解的對比，驗(yàn)證了數(shù)值模型的有效性。其次利用該模型研究了流場中不同點(diǎn)的記憶速度勢隨時(shí)間的變化特點(diǎn)。最后根據(jù)記憶速度勢隨時(shí)間的變化特性，提出了利用Laguerre函數(shù)[9]對記憶速度勢時(shí)間變量進(jìn)行級數(shù)逼近，并通過引入一放縮系數(shù)加快了級數(shù)的收斂速度。

1基礎(chǔ)理論

1.1內(nèi)外場匹配模型

根據(jù)文獻(xiàn)[10]，假定流場為不可壓縮的理想流體，則流場中的物理量可以用流體速度勢Φ來進(jìn)行描述。為建立三維時(shí)域匹配模型，引入一虛擬控制面，如圖1所示。

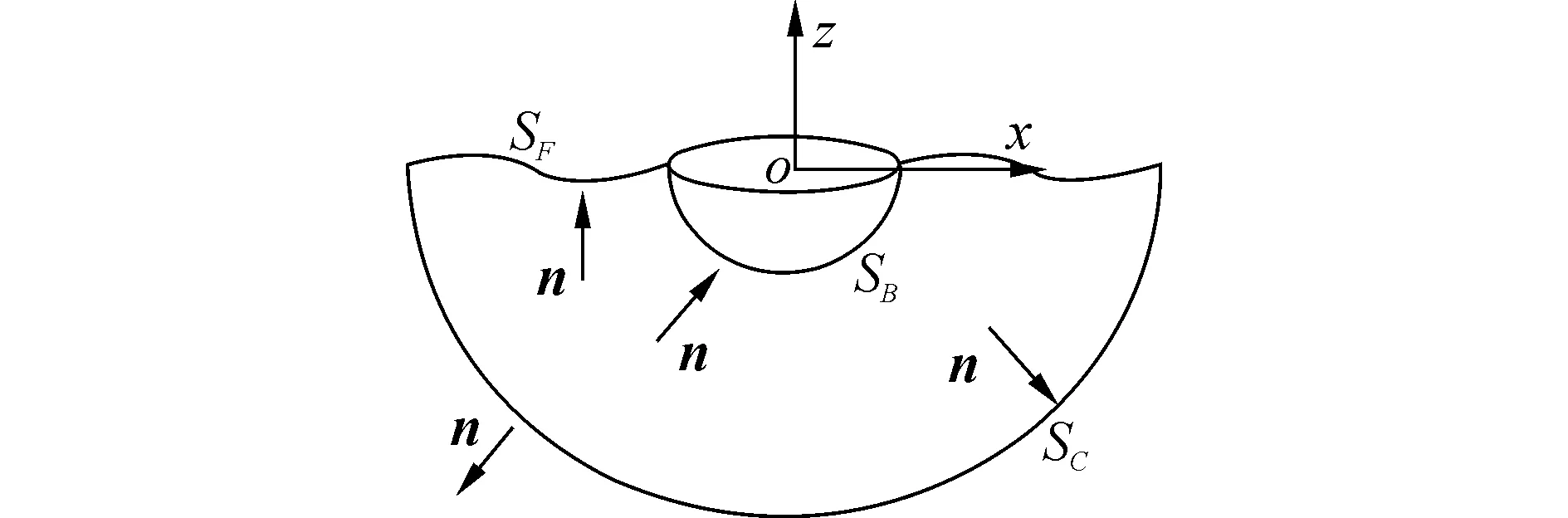
圖1　內(nèi)外域匹配求解示意圖Fig.1　Coordinate system and boundary surface

流體速度勢在內(nèi)域滿足以Rankine源所建立的邊界積分方程：

(1)

流體速度勢在外域滿足以時(shí)域自由面格林函數(shù)所建立的邊界積分方程：

(2)

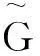
(3)

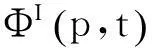
(4)

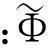
同理，速度勢ΦII在外域滿足的邊界積分方程(2)也可以離散為相應(yīng)的矩陣形式

(5)

式中：rC表示外域所滿足的邊界積分方程的時(shí)間卷積項(xiàng)。

在虛擬控制面SC上，流體速度勢及其法向?qū)?shù)應(yīng)滿足如下連續(xù)條件：

(6)

通過速度勢在內(nèi)域滿足的邊界積分方程式(4)和外域滿足的邊界積分方程式(5)，便可以得到內(nèi)外域匹配求解方程組：

(7)

式中矩陣的系數(shù)如下

(8)

(9)

(10)

(11)

由式(7)，在求解流場速度勢時(shí)，只有虛擬控制面SC上涉及了時(shí)域自由面格林函數(shù)波動項(xiàng)的計(jì)算。

1.2流場速度勢分解

由于流體速度勢所滿足的場方程、邊界條件和初始條件均是線性化的，故可以對流體速度勢進(jìn)行線性化分解[11]

(12)

式中：ΦI、ΦD和Φk分別為入射波速度勢、繞射波速度勢和輻射波速度勢，其中ΦI為已知量，ΦD和Φk為待求解的未知量。

對于輻射波速度勢Φk，根據(jù)其所代表的物理意義，可以將其分解為與時(shí)間無關(guān)的瞬時(shí)速度勢Ψk和與時(shí)間相關(guān)的記憶速度勢χk:

(13)

根據(jù)瞬時(shí)速度勢和記憶速度勢在內(nèi)外域滿足的邊界條件和初始條件[3]，利用式(7)便可求出相應(yīng)的值。根據(jù)線性化的Bernoulli方程[10]便可求出對應(yīng)的輻射波力

(14)

式中：μjk和Kjk分別為與頻率無關(guān)的附加質(zhì)量和時(shí)域延遲函數(shù)。其可以相應(yīng)的轉(zhuǎn)化為頻域附加質(zhì)量Ajk和阻尼系數(shù)Bjk:

(15)

(16)

1.3時(shí)間卷積積分項(xiàng)

(17)

(18)

根據(jù)記憶速度勢隨時(shí)間的變化特性，為加快級數(shù)的收斂速度，引入一放縮系數(shù)a:

(19)

(20)

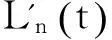
(21)

2數(shù)值結(jié)果

2.1匹配邊界元有效性驗(yàn)證

利用時(shí)域快速匹配邊界元法求解浮體和波浪相互作用問題時(shí)，影響計(jì)算精度的主要因素有時(shí)間步長、邊界網(wǎng)格數(shù)目、自由面網(wǎng)格形式、虛擬控制面和物體之間的距離。

為討論自由面網(wǎng)格形式的影響，針對相同工況，分別選擇了矩形網(wǎng)格、輻射狀網(wǎng)格和矩形三角形混合網(wǎng)格進(jìn)行了計(jì)算，通過與解析解[12]的對比驗(yàn)證發(fā)現(xiàn)輻射狀的自由面網(wǎng)格能夠最好的描述輻射波和繞射波的傳播，如圖2所示，圖中半球半徑為1 m，控制面半球半徑為5 m。此與輻射和繞射波代表外傳柱面波的物理意義相一致。

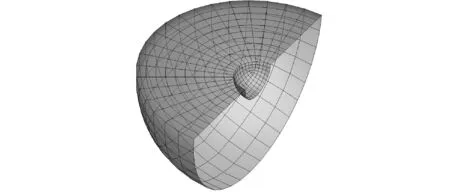
圖2　匹配邊界元網(wǎng)格劃分示意圖Fig.2　Grid pattern for Rankine-Green method

為討論時(shí)間步長對計(jì)算結(jié)果的影響，針對相同工況，分別選取了△t=0.02、0.01、0.005 s進(jìn)行了計(jì)算。計(jì)算得到的無量綱時(shí)域延遲函數(shù)如圖3所示，3條曲線幾乎重合。此外，針對邊界網(wǎng)格數(shù)目和虛擬控制面與物體之間的距離也做了同樣的對比分析。最后，考慮數(shù)值計(jì)算精度和計(jì)算效率，在文章后續(xù)計(jì)算中，自由面劃分為輻射式網(wǎng)格，計(jì)算時(shí)間步長選為0.01 s，虛擬控制面和物面間距為5倍的物體特征長度，網(wǎng)格數(shù)目為物面130、自由面200、控制面150。

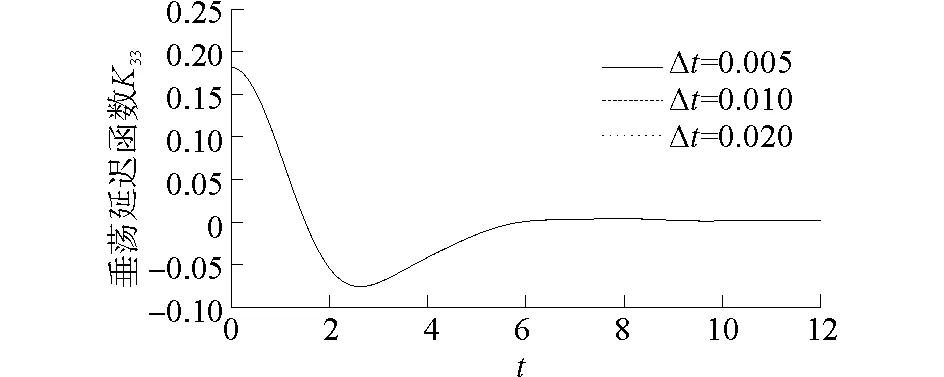
圖3　時(shí)間步長對計(jì)算結(jié)果的影響Fig.3　Influence of time step on the numerical results interval

對于半球在靜水中做強(qiáng)迫垂蕩運(yùn)動，分別計(jì)算了其附加質(zhì)量系數(shù)和阻尼系數(shù)，如圖4、5所示。由圖可知，利用本文建立的快速時(shí)域匹配邊界元法計(jì)算的結(jié)果與文獻(xiàn)[12]提供的解析解符合良好，說明本文提供的數(shù)值模型能夠準(zhǔn)確模擬波浪和浮體相互作用的流場。

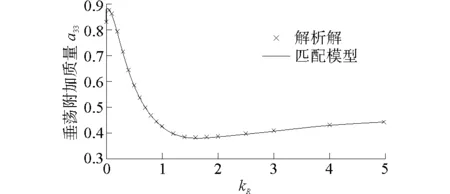
圖4　無因次附加質(zhì)量系數(shù)Fig.4　Non-dimensional added mass coefficient

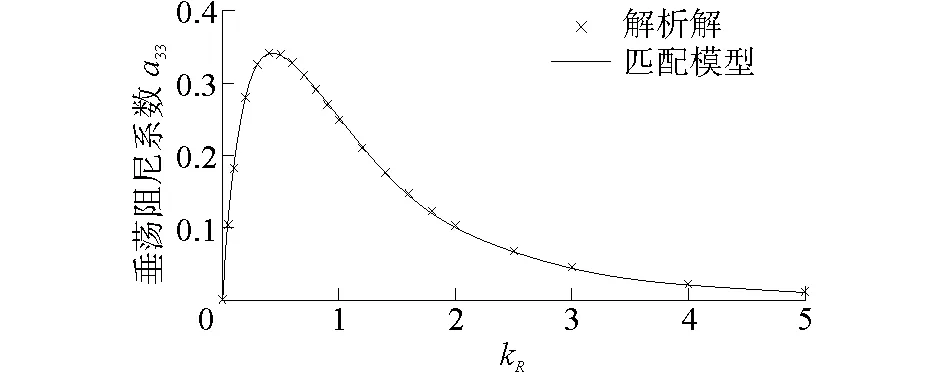
圖5　無因次興波阻尼系數(shù)Fig.5　Non-dimensional damping coefficient

2.2Laguerre函數(shù)有效性驗(yàn)證

為驗(yàn)證Laguerre函數(shù)的有效性，首先對記憶速度勢隨時(shí)間的變化特性進(jìn)行了研究。記憶速度勢代表浮體干擾形成表面波浪，開始波浪傳播之后的那部分速度勢，并且隨時(shí)間逐漸衰減，如圖6所示，圖中點(diǎn)1位于虛擬控制面和自由表面相交處(5,0,0)，點(diǎn)2位于虛擬控制面的中部(4.33,0.00,2.50)，點(diǎn)3位于虛擬控制面的底部(0,0,5)。圖6表明隨著場點(diǎn)遠(yuǎn)離自由面，記憶速度勢的變化逐漸趨于平緩，此與記憶速度勢代表物體興波部分速度勢的物理意義相一致；且記憶速度勢隨時(shí)間出現(xiàn)一個(gè)較大的脈沖峰以后，便開始迅速衰減，此與修正Laguerre函數(shù)中的指數(shù)函數(shù)部分相符合，初步說明了利用Laguerre函數(shù)進(jìn)行記憶速度勢時(shí)間變量級數(shù)逼近的可行性。

圖6　記憶速度勢隨時(shí)間變化Fig.6　 Memory potential for different points

根據(jù)圖6中的3組數(shù)據(jù)，本文對隨時(shí)間變化最為劇烈的點(diǎn)1進(jìn)行了Laguerre函數(shù)逼近研究。在不引入放縮系數(shù)的情況下，函數(shù)逼近隨級數(shù)項(xiàng)數(shù)的變化如圖7所示，絕對誤差隨項(xiàng)數(shù)的變化如圖8所示。由圖可知，隨著逼近級數(shù)項(xiàng)數(shù)的增加，級數(shù)解越趨近于原數(shù)據(jù)，但是收斂效果隨項(xiàng)數(shù)的增加改善較為緩慢，例如當(dāng)級數(shù)項(xiàng)數(shù)增加一倍時(shí)，逼近絕對誤差縮小不到一倍，而計(jì)算求解矩陣的維數(shù)卻大大增加。

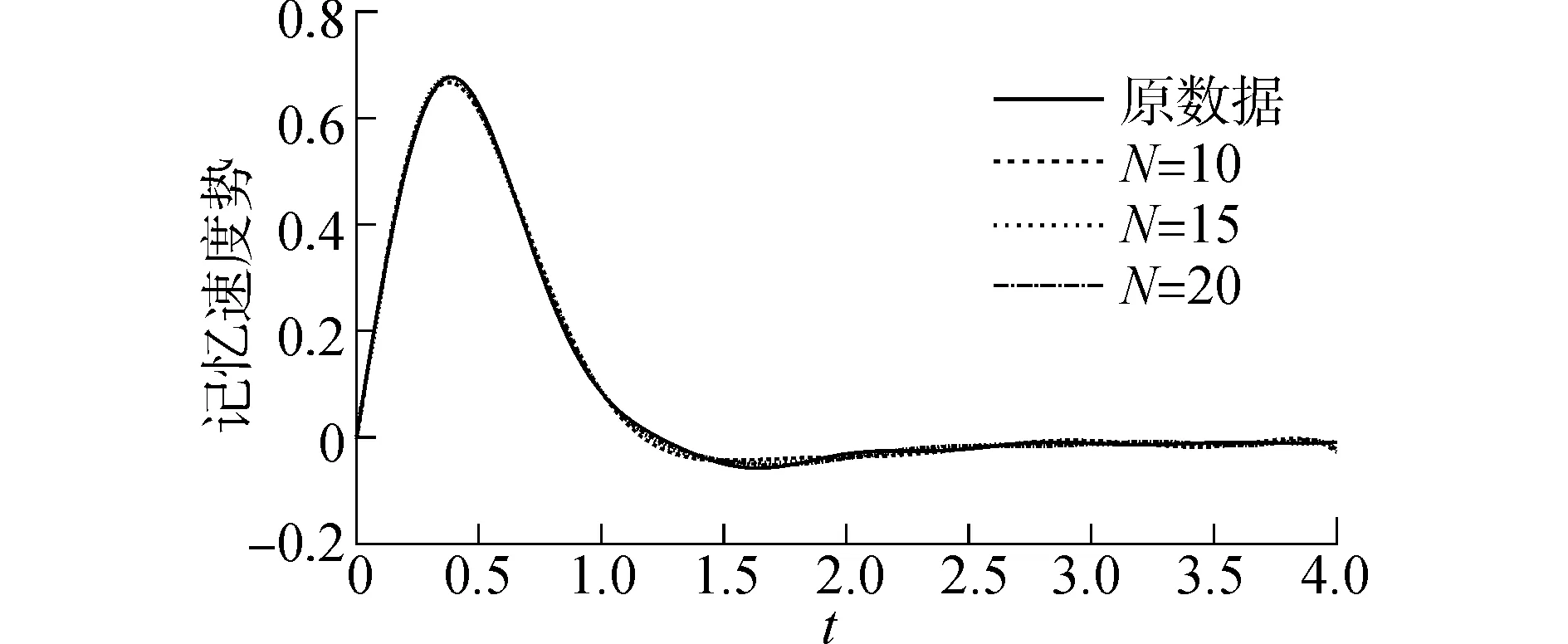
圖7　Laguerre級數(shù)逼近精度與截?cái)囗?xiàng)數(shù)的關(guān)系(a=1)Fig.7　Relationship between series approximation and 　　truncated series terms (a=1)

圖8　Laguerre級數(shù)逼近絕對誤差與截?cái)囗?xiàng)數(shù)的關(guān)系(a=1)Fig.8　Relationship between absolute error and truncated 　　series terms (a=1)

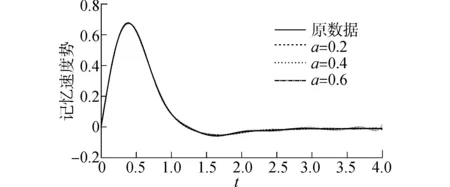
圖9　Laguerre級數(shù)逼近與放縮系數(shù)的關(guān)系(N=15)Fig.9　Relationship between series approximation and　　 flexible parameter (N=15)

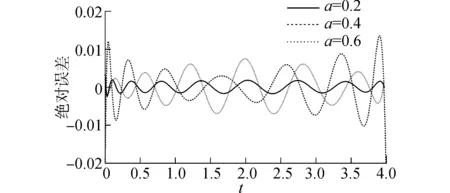
圖10　Laguerre級數(shù)逼近絕對誤差與放縮系數(shù)的關(guān)系(N=15)Fig.10　Relationship between absolute error and flexible 　　parameter (N=15)

為了增加Laguerre級數(shù)逼近的收斂速度，同時(shí)又不增加計(jì)算機(jī)求解負(fù)擔(dān)，引入了放縮系數(shù)的概念，如式(21)所示。由圖10可知，隨著放縮系數(shù)的減小，相對誤差逐漸減小，當(dāng)放縮系數(shù)等于0.2時(shí)，級數(shù)項(xiàng)取為15的結(jié)果要明顯優(yōu)于不取放縮系數(shù)的級數(shù)項(xiàng)取為20的結(jié)果，如圖11所示。由此可以確定，通過引入放縮系數(shù)，可以利用較少的項(xiàng)數(shù)來逼近函數(shù)的真解，從而確保了利用Laguerre函數(shù)進(jìn)行記憶速度勢時(shí)間變量進(jìn)行級數(shù)逼近的經(jīng)濟(jì)性和可行性。

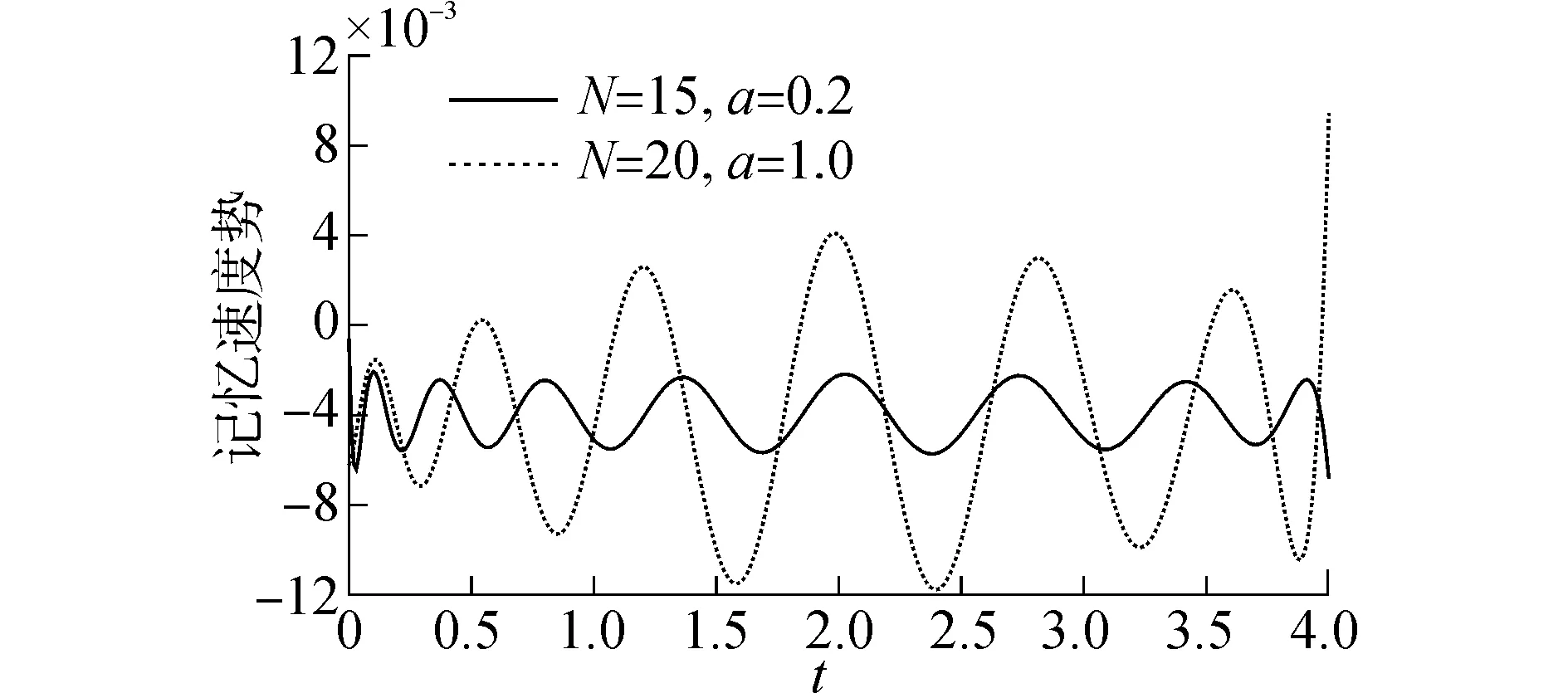
圖11　放縮系數(shù)對級數(shù)收斂速度影響Fig.11　 Influence of flexible parameter and series terms

4結(jié)論

本文通過引入虛擬控制面，將流場劃分為內(nèi)域和外域，并根據(jù)速度勢及其法向?qū)?shù)在控制面上連續(xù)的條件建立了時(shí)域快速匹配邊界元模型。此外，提出了利用Laguerre函數(shù)對記憶速度勢的時(shí)間軸進(jìn)行級數(shù)逼近，以解析計(jì)算時(shí)間卷積積分的思路，并通過引入一放縮系數(shù)，大大加快了級數(shù)的收斂速度。通過對計(jì)算結(jié)果的分析，得到以下結(jié)論：

1)通過與解析解的對比表明本文建立的內(nèi)外場時(shí)域快速匹配邊界元法具有較高的數(shù)值計(jì)算精度，且由求解矩陣可知，時(shí)域快速匹配邊界元法與直接邊界元法相比具有較高的計(jì)算效率，為研究浮體和波浪相互作用下流場的特性提供了一種精確、高效的方法；

2)自由面劃分為輻射狀網(wǎng)格，控制面距離物面為5倍的物體的特征尺度，時(shí)間步長取為0.01 s時(shí)，時(shí)域快速匹配邊界元法便能給出令人滿意的計(jì)算結(jié)果；

3)代表浮體興波之后流場特性的記憶速度勢在出現(xiàn)一個(gè)很大的峰之后，隨時(shí)間迅速衰減，當(dāng)t=2.5 s后，基本趨于平緩；

4)利用Laguerre函數(shù)對記憶速度勢的時(shí)間變量做級數(shù)逼近時(shí)，隨著級數(shù)項(xiàng)數(shù)的增加，級數(shù)逐漸收斂，但級數(shù)收斂速度較為緩慢；

5)分析Laguerre函數(shù)及其正交權(quán)函數(shù)的性質(zhì)，引入一放縮系數(shù)，數(shù)值結(jié)果顯示，放縮系數(shù)可大大加快級數(shù)的收斂速度，N=15，a=0.2的逼近結(jié)果要明

顯的優(yōu)于N=20，a=1時(shí)的結(jié)果,保證了時(shí)域快速解析匹配邊界元的可行性與高效性。

參考文獻(xiàn)：

[1]SEO M G, KIM Y. Numerical analysis on ship maneuvering coupled with ship motion in waves[J]. Ocean engineering, 2011, 38(17/18): 1934-1945.

[2]BECK R, LIAPIS S. Transient motions of floating bodies at zero forward speed[J]. Journal of ship research, 1987, 31(3):164-176.

[3]KING B. Time-domain analysis of wave exciting forces on ships and bodies[R]. Michigan: University of Michigan, 1987.

[4]CLéMENT A H. An ordinary differential equation for the Green function of time-domain free-surface hydrodynamics[J]. Journal of engineering mathematics, 1998, 33(2): 201-217.

[5]SONG M J, KIM K H, KIM Y. Numerical analysis and validation of weakly nonlinear ship motions and structural loads on a modern containership[J]. Ocean engineering, 2011, 38(1): 77-87.

[6]SEO M G, YANG K K, PARK D M, et al. Numerical analysis of added resistance on ships in short waves[J]. Ocean engineering, 2014, 87: 97-110.

[7]LIU S, PAPANIKOLAOU A. Application of a nonlinear time domain hybrid method to the study of a semi-submersible in waves[C]//Proceedings of the 22nd international offshore (ocean) and polar engineering conference,Rhodes, Greece, 2012.

[8]韓旭亮, 段文洋. 時(shí)域匹配直接邊界元方法及其數(shù)值特性[J]. 哈爾濱工程大學(xué)學(xué)報(bào), 2013(7): 837-843.

HAN Xuliang, DUAN Wenyang. Study on the numerical characteristics of time domain matching direct boundary element method[J]. Journal of Harbin engineering university, 2013(7): 837-843.

[9]ABRAMOWITZ M, STEGUN I A. Handbook of mathematical functions: With formulas, graphs, and mathematical tables[M]. (s.l.):Courier Dover Publications, 1972.

[10]WEHAUSEN J V, LAITONE E V. Surface waves[M]. Springer, 1960.

[11]TANG K, ZHU R, MIAO G, et al. Domain decomposition and matching for time-domain analysis of motions of ships advancing in head sea[J]. China ocean engineering, 2014, 28: 433-444.

[12]HULME A. The wave forces acting on a floating hemisphere undergoing forced periodic oscillations[J]. Journal of fluid mechanics, 1982, 121: 443-463.

本文引用格式：

李志富，任慧龍，石玉云，等. Laguerre函數(shù)在時(shí)域匹配邊界元中的應(yīng)用研究[J]. 哈爾濱工程大學(xué)學(xué)報(bào)， 2016, 37(5): 629-633.

LI Zhifu，REN Huilong，SHI Yuyun， et al. Application of Laguerre function in the time domain Rankine-Green panel method[J]. Journal of Harbin Engineering University, 2016, 37(5): 629-633.

Application of Laguerre function in the time domain Rankine-Green panel method

LI Zhifu，REN Huilong，SHI Yuyun，LI Hui

(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract：The divergence phenomenon will happen when the transient free surface Green function method is adopted to simulate the motion response of the ships with large flare. To avoid that problem, the Rankine-Green panel method is proposed , and the accuracy of this method is verified by the comparision with the analytical solutions. Then the hybrid method is used to investigate the variation properties of the memory velocity potential wiht respect to time, and the Laguerre function is introduced to express the memory potentials in the Laguerre series form. Therefore, the temporal convolution integral of the memory potentials with the Green function can be computed analytically, which ensures the long time simulations. Besiedes, to accelerate the convergence speed of the Laguerre series, a flexible parameter is introduced and its features are discussed. The numerical results show that the temporal variable of the memory potential can be approximated by less Laguerre series terms with a flexible parameter, which means that the Laguerre series can give a reasonable description of the impulse properties of the memory velocity potential.

Keywords：Laguerre function; Rankine-Green panel method; temporal convolution integral; series approximation; flexible parameter

收稿日期：2015-04-10.

基金項(xiàng)目：國家“973”計(jì)劃項(xiàng)目(2011CB3703)；國家自然科學(xué)基金資助項(xiàng)目(51109046).

作者簡介：李志富(1990-), 男, 博士研究生； 通信作者：任慧龍, E-mail：renhuilong@263.net.

DOI:10.11990/jheu.201504023

中圖分類號：O352

文獻(xiàn)標(biāo)志碼：A

文章編號：1006-7043(2016)05-0629-05

網(wǎng)絡(luò)出版時(shí)間：2016-04-11.

任慧龍(1965-), 男, 教授, 博士生導(dǎo)師.