軍事工程搶修任務規劃問題研究
文/何苗 王強 荀毅 魏曉航
?
軍事工程搶修任務規劃問題研究
文/何苗王強荀毅魏曉航
摘 要:本文針對戰時軍事工程搶修問題,研究在搶修資源有限的情況下,如何科學合理地安排搶修活動,最大限度恢復軍事工程防護能力。通過引入搶修時間窗,同時考慮軍事工程搶修的時間約束和邏輯約束,建立了使軍事工程防護能力恢復最大的搶修任務規劃優化模型,設計了一種離散型粒子群算法對模型求解。最后,以戰場軍事工程搶修任務為背景,用算例驗證了模型的實用性和算法的有效性。
關鍵詞:軍事工程搶修;任務規劃;時間窗;離散粒子群算法
現代信息化戰爭中,廣泛應用高新技術,特別是精確制導武器和激光、隱形技術的發展和普及,使得軍事偵察手段日益先進,武器系統命中率越來越高,破壞性越來越大。軍事工程設施作為保障部隊執行作戰指揮、通信聯絡、后勤補給等任務的基本平臺,是敵方攻擊的首要目標。因此,如何快速搶修戰損的軍事工程,盡快恢復其保障能力,是贏得未來戰爭主動權的關鍵。在戰爭中,軍事工程搶修最重要的特點就是時效性,要求使用一切可以利用的搶修資源,在盡可能短的時間內,對軍事工程的毀傷部分進行修繕加固,使之恢復防護能力,抵御敵軍武器系統攻擊。軍事工程搶修任務具有不同的技術特點,同時,各搶修分隊力量構成存在著差異,搶修資源有限,不同搶修分隊完成同一搶修任務的時間不同。因此,搶修資源優化配置對盡可能完成更多的軍事工程搶修任務,最大限度恢復軍事工作在作戰體系中的保障能力具有顯著影響,軍事工程搶修任務規劃問題也就成了一個需要研究解決的問題。
目前,對軍事工程戰損評估、搶修組織實施和搶修裝備技術等方面均已有深入研究[1~3]。但是在軍事工程搶修資源配置和搶修任務規劃問題方面的研究甚少。關于搶修任務規劃調度問題的研究,主要針對戰場裝備搶修及應急資源調度問題,建立基于排隊論的數學模型[4]、多需求點多資源的二層優化調度模型[5]、非線性規劃模型[6],采用蟻群算法[7]、遺傳算法[8]、蜂群算法[9]等優化算法對問題進行求解,為軍事工程搶修任務規劃問題的研究提供了新的思路和方法。本文將針對軍事工程搶修任務規劃問題的特殊性,建立搶修任務規劃模型,并采用一種離散粒子群算法對該模型進行求解。
1.軍事工程搶修任務規劃模型
1.1問題描述
軍事工程搶修任務規劃是根據戰場態勢和軍事工程戰損評估結果,確定軍事工程搶修目標任務的搶修時間窗口及所需搶修資源。針對每一個軍事工程搶修項目,結合戰區內的工程保障力量,科學合理地組織搶修資源,組建工程搶修分隊,在軍事工程搶修任務要求的時間窗口內及時做好搶修工作,最大限度恢復軍事工程防護能力。
軍事工程搶修任務規劃問題可以描述為:在某一戰斗區域內有M個軍事工程搶修保障單位,每個單位有不同的保障資源,可以組成一個應急工程搶修分隊。經現場調查評估,結合戰場態勢,認定共有N個軍事工程受到敵方攻擊受損,急需通過工程保障力量修繕恢復其防護能力。由于工程類別以及受損程度各異,同時,各個搶修分隊力量構成不同,致使不同搶修分隊完成同一工程搶修任務的時間不同。另外,由于各個軍事工程在整個作戰體系中的地位作用差異以及戰場態勢的不同,各個搶修任務必須在一定時間范圍內執行,即任務時間窗約束。
1.2模型建立
設定軍事工程搶修任務集合N={1,2,L,n },n為搶修任務數目,?j∈ N,[tsj,tej]為其搶修時間窗,tsj為其允許搶修的最早開始時刻,tej為其允許搶修的最晚結束時刻。Tj表示某個軍事工程搶修分隊開始對目標工程j進行搶修的開始時刻。?k∈ N,pk表示軍事工程k的任務優先級,也可以認為是軍事工程k在整個作戰體系中的重要性指標。
軍事工程搶修分隊集合為M={1,2,L m},m為搶修分隊的數目。?j∈ N,?i∈ M,tij表示搶修分隊i對軍事工程j進行搶修的時間長度。搶修任務目標之間的線路為:,t d k j表示某一搶修分隊沿線路(k, j)轉移的時間。搶修分隊與搶修任務目標之間的線路為:。tdik表示搶修分隊i從駐地出發,沿線路轉移到任務目標(i, k)的時間。
綜上所述,可建立該問題的數學模型,目標函數:
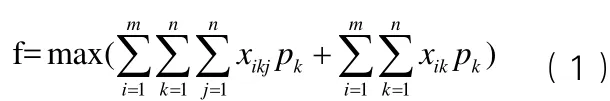
由于資源的有限性及搶修任務的多樣性,目標函數設定為完成軍事工程搶修任務優先級之和最大。
約束條件:
(1)每個軍事工程至多由一個搶修分隊完成搶修一次(小于1意味著沒有針對該軍事工程進行搶修):
(2)搶修分隊對任務目標搶修的時間必須在時間窗范圍內:
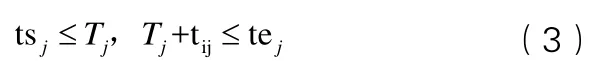
(3)每個搶修分隊至少對一個軍事工程完成搶修任務。
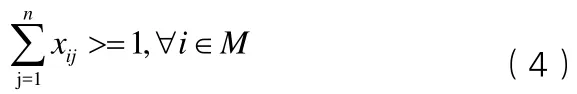
2.算法設計
2.1基本原理
粒子群優化算法(Particle Swarm Optimization, PSO)是由James Kennedy和Russell Eberhart于1955年提出的一種基于群智能的隨機搜索算法[10]。基本粒子群算法的思想是模擬鳥群覓食的過程,將問題解空間中一個可行解看作一只鳥及所謂的“粒子”。這些鳥通過不停地改變自己的位置和速度去覓食,直到成功覓食(即最優解)[11]。基本粒子群算法所描述的粒子位置和速度都是連續變量,難以求解在離散空間中建模的任務調度問題。本文將采用一種適合軍事工程搶修任務規劃的離散粒子群算法。
2.2算法求解步驟
針對軍事工程搶修任務規劃問題,每個粒子代表一個可行解,即任務分配方案。用自然數對任務進行編碼,粒子編碼中的每一個自然數代表搶修分隊,修任務數量為粒子編碼長度。如圖所示,有10個搶修任務,3個搶修分隊。分隊1負責任務3和任務5,其中任務2和任務9沒有完成。得到一個粒子編碼為(2,0,1,2,1,3,2,3,0,3)。
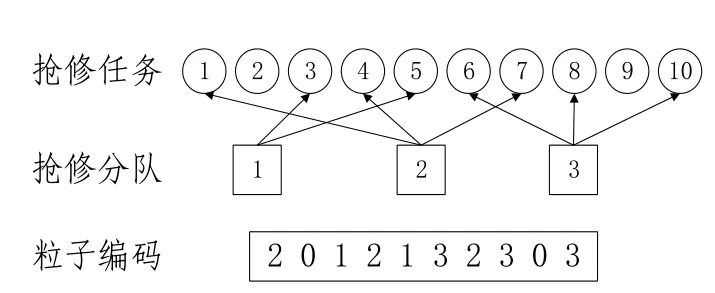
圖1 離散粒子的編碼方式
結合軍事工程搶修任務規劃問題的特點,本文采用式(5)分步計算和修改粒子位置,首先是當前粒子內部分量之間的交換,再根據粒子的歷史最佳位置修改當前位置,然后根據粒子群體的最佳位置調整當前粒子位置。

其中,ω,c
1
,c
2
為擾動因子,其取值范圍為[0,1]。函數
表示X
i
的第a個分量與第b個分量交換,a,b均為1到n之間的隨機整數(a>b)。并以c
1
為概率對位置交換進行擾動,
。
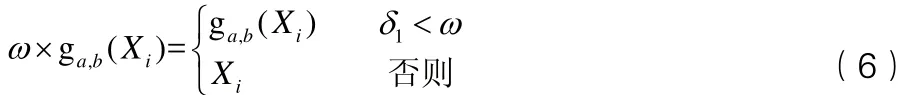
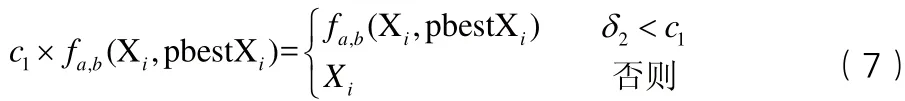
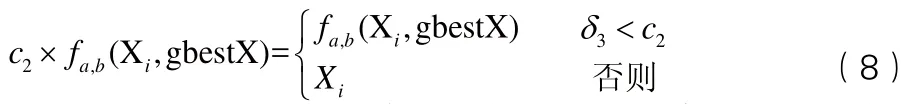
經過上述3個步驟,當前粒子位置調整完成,得到一個新解。利用DPSO算法求解的流程如圖2所示。
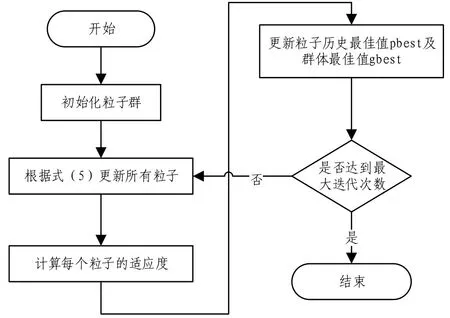
圖2 DPSO算法求解流程
3.算例
在某作戰區域內,有10個軍事工程搶修任務,分布在不同地里位置。共組建3個不同的工程搶修分隊,它們從駐地到各個軍事工程搶修任務點的轉移時間如表1所示,搶修分隊完成各個搶修任務的時間如表2所示,搶修分隊在各個搶修任務點之間的轉移時間如表3所示。各個搶修任務接受搶修的時間窗及任務優先級如表4所示。
利用DPSO算法對模型進行求解,設定種群規模為20,最大迭代次數為1000次,獨立運行20次,目標函數值穩定在53,可得軍事工程搶修任務方案如表5所示。由于時間約束的限制,搶修任務3、任務5和任務7未能完成。
4.結語
現代戰爭中,軍事工程設施在體系對抗中具有重要作用,對戰損軍事工程組織實施搶修具有較強的時間限制,即要在規定時間范圍內完成盡可能多的搶修任務,最大限度恢復軍事工程體系對抗中的防護能力。本文研究了基于搶修時間窗的軍事工程搶修任務規劃問題,綜合考慮搶修活動的時間約束和邏輯約束,建立了搶修任務規劃模型,并利用DPSO算法求解。算例表明,該模型和算法能較好地解決軍事工程搶修任務規劃問題。
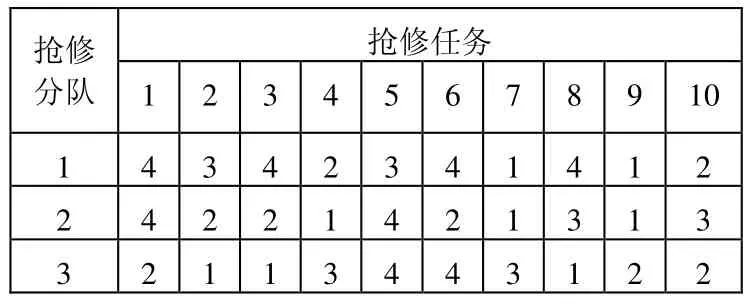
表1 搶修分隊到各目標的轉移時間
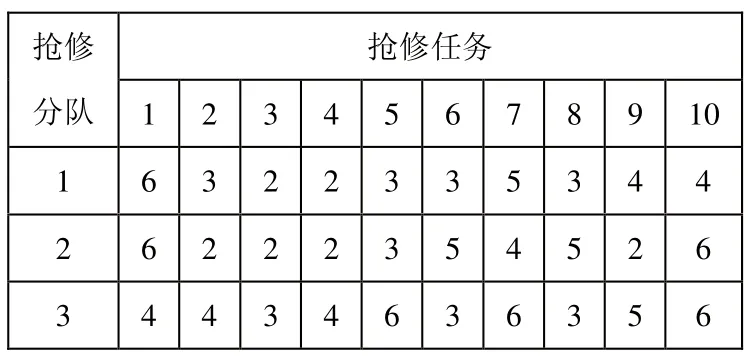
表2 搶修分隊完成任務的時間
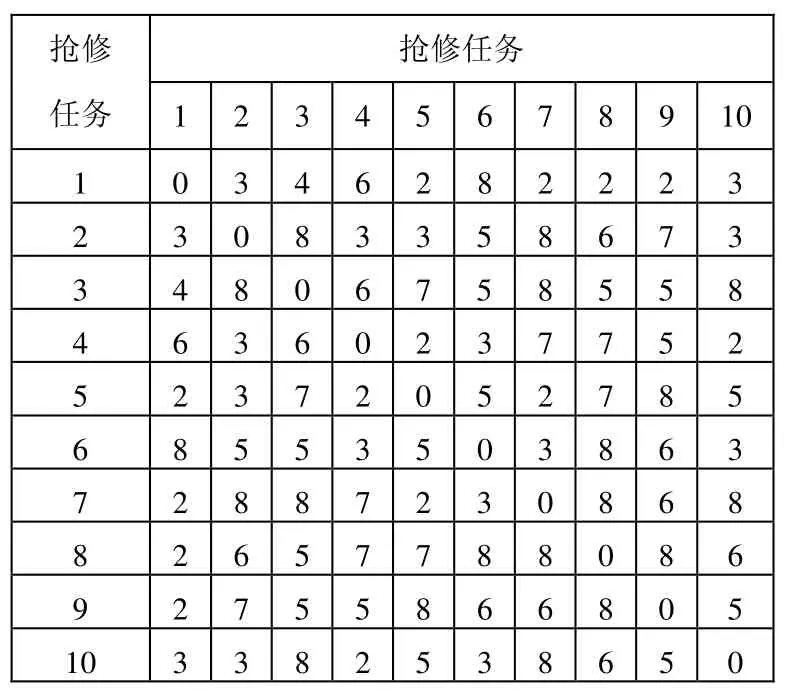
表3 各個搶修任務目標之間的轉移時間
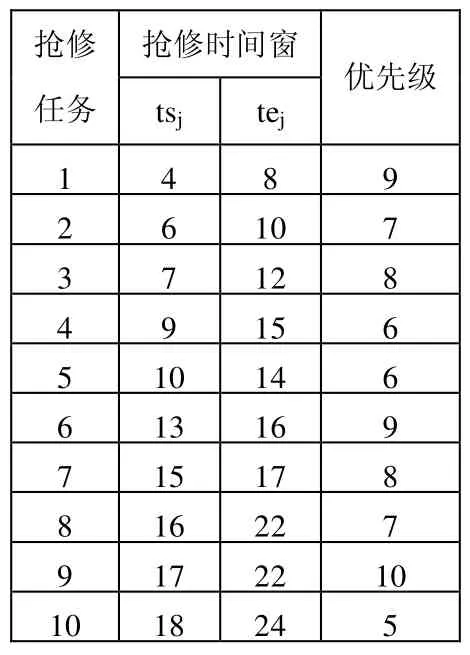
表4 任務時間窗及優先級
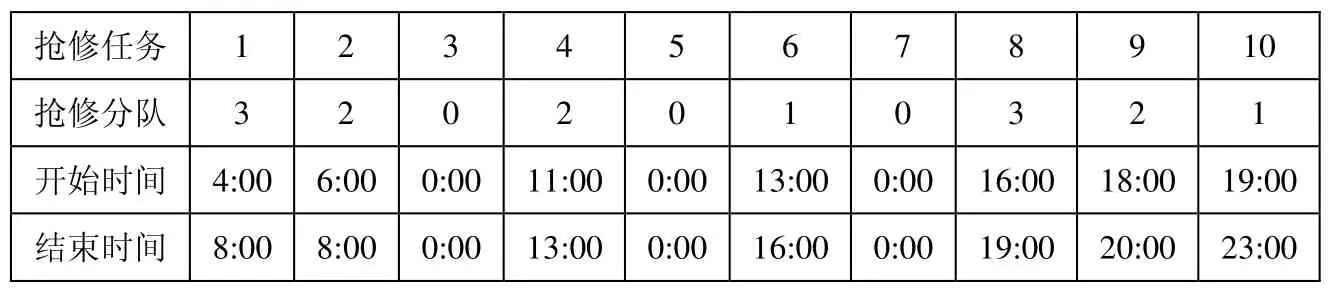
表5 搶修方案
(作者單位:中國人民解放軍后勤工程學院)
參考文獻
[1]王鳳山,吳禮發.軍事工程毀傷評估與搶修計劃生成機制研究[J].計算機與數字工程,2011,39(10):96~100.
[2]袁輝,王鳳山.軍事工程毀傷評估的組合智能模型[J].計算機工程與應用,2013,49(9):23~28.
[3]王鳳山.地下工程搶修作業計劃與控制要求及其策略研究[J].系統科學學報,2010,18(4):53~57.
[4]王小飛,蘇凡囤,王海濤,鐘曉谷.基于排隊論的戰時工程裝備搶修任務調度[J].兵工自動化,2012,31(10):29~32.
[5]曹繼平,宋建社,古西睿,何志德.戰場搶修多需求點多資源二層優化調度模型[J].系統工程與電子技術,2008,30(8):1509~1513.
[6]呂學志,于永利,張柳,陳樂,董岳,劉文武.資源約束的拼件維修模型與粒子群求解算法[J].系統工程理論與實踐,2013,33(4):1013~1018.
[7]蔡紀偉,賈云獻,孫曉,張曉康.蟻群算法在戰損裝備搶修任務指派中的應用研究[J].數學的實踐與認識,2012,42 (19):160~165.
[8]王銳,李羚偉,郭波,馬武彬.一種基于多目標多約束的戰時搶修力量調度[J].兵工自動化,2010,29(1):34~37.
[9]王浩.基于蜂群算法的戰時毀傷裝備維修任務調度研究[J].火力與指揮控制,2009,34(S1):141~144.

