基于RBF神經網絡的功率倒置波束形成算法

張寶軍, 袁　潔

(西安郵電大學 電子工程學院， 陜西 西安 710121)

基于RBF神經網絡的功率倒置波束形成算法

張寶軍, 袁潔

(西安郵電大學 電子工程學院， 陜西 西安 710121)

摘要:提出一種基于徑向基函數神經網絡的功率倒置波束形成算法。該算法將計算功率倒置算法的最佳權向量的兩個變量，即接收信號的自相關矩陣和參考信號與接收信號的互相關矩陣輸入RBF神經網絡，對網絡進行訓練，通過只提取接收信號自相關矩陣的有用信息輸入網絡，減少網絡訓練時間，使之逼近功率倒置的最佳權向量。仿真結果表明，該算法能準確的逼近功率倒置的最佳權向量，減小了運算量。

關鍵詞:波束形成；功率倒置；RBF神經網絡

自適應波束形成技術[1]是智能天線的關鍵技術之一，主要用于雷達、聲吶、軍事抗干擾通信等領域。常用的自適應波束形成算法主要有最小均方(LeastMeanSquare,LMS)算法[2]、采樣矩陣求逆(SampleMatrixInversion,SMI)算法[3]、遞歸最小均二乘(RecursiveLeastSquare,RLS)算法[4]等。LMS算法簡便靈活易于實現，但收斂速度較慢；SMI算法收斂速度較快，但是需要矩陣求逆運算，復雜度較高；RLS算法收斂速度快，但是計算量比較大。

波束形成技術中的功率倒置(PowerInversion,PI)算法，雖然，對信號進行處理時，不需要區分信號與干擾[5]，但在干擾信號相關信息不明確的情況下，利用功率倒置算法進行干擾信號的處理時，存在矩陣之間的運算以及矩陣求逆運算，運算量較大。

本文利用徑向基函數 (RadicalBasisFunction，RBF)神經網絡[6-7]有較強的函數逼近的特點，給出一種基于徑向基函數神經網絡的功率倒置波束形成算法。

1功率倒置算法的基本原理

功率倒置算法是以參考信號與陣列輸出之差的均方最小為目標函數，根據輸入輸出，調節陣列的權向量，使目標函數達到最小，從而達到自適應調節的目的[8]。功率倒置陣列的結構原理如圖1所示。x1,x2,…,xM是陣元的接收信號，1,w2，…,wM是陣元權值，輸出y是接收信號與權值的加權求和。

圖1　功率倒置陣列結構

設天線陣列陣元個數為M，保持第1支路陣元的權值為固定值1，自適應算法調節其余支路陣元的權值，使得陣列輸出功率為最小。將第1支路陣元接收到的信號作為參考信號，調節其余的2～M個陣元權向量使得參考信號與輸出信號的均方誤差最小。

陣元接收到的信號分別為x1,x2,…,xM，第2～M個陣元接收到的信號可表示為[8]

x=[x2,x3,…,xM]T,

(1)

第2～M個陣元的權矩陣可表示為[8]

w=[w2,w3,…,wM]T,

(2)

則陣列的輸出為[8]

y=x1-wHx,

(3)

式(3)取模的平方再求期望得[8]

(4)

對式(4)中的w求梯度得[8]

ξ=-2rxx1+2Rxxw,

(5)

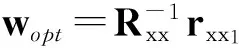
(6)

其中rxx1=E[xx1]，為參考信號和第2～M支路陣元信號的互相關矩陣，Rxx=E[xxH]為第2～M支路陣元上信號的自相關矩陣。

由式(6)可以看出，求解功率倒置陣列的最佳權向量時要對矩陣進行求逆運算。矩陣求逆運算實質上為線性方程組的求解，其計算復雜度為O(n3)(其中n是線性方程組的個數)，由此可以看出求解過程中的運算量較大。

2功率倒置的RBF實現

將互相關矩陣rxx1和自相關矩陣Rxx作為RBF神經網絡的輸入，對網絡進行訓練，使之逼近功率倒置的最佳權向量wopt。由于自相關矩陣Rxx是Hermite矩陣[9]，即

Rxx(i,j)=Rxx(j,i)，

其對角元素不含相位信息，因此可以只取自相關函數Rxx上三角部分或者下三角部分，按照實部、虛部分開，作為RBF神經網絡的輸入[10]。這樣可以減少自相關函數的維數，加快訓練RBF神經網絡的過程，進一步縮短算法運算時間。

2.1RBF網絡結構

RBF神經網絡是以函數逼近理論為基礎構造的一類前向網絡。由式(6)可知，功率倒置算法權向量的求解就是自相關矩陣Rxx和互相關矩陣rxx1到權向量的非線性映射問題，而用RBF神經網絡能將任意維數的輸入空間映射到任意維的輸出空間來逼近任何非線性函數，可以實現該非線性映射。網絡拓撲結構圖2所示。

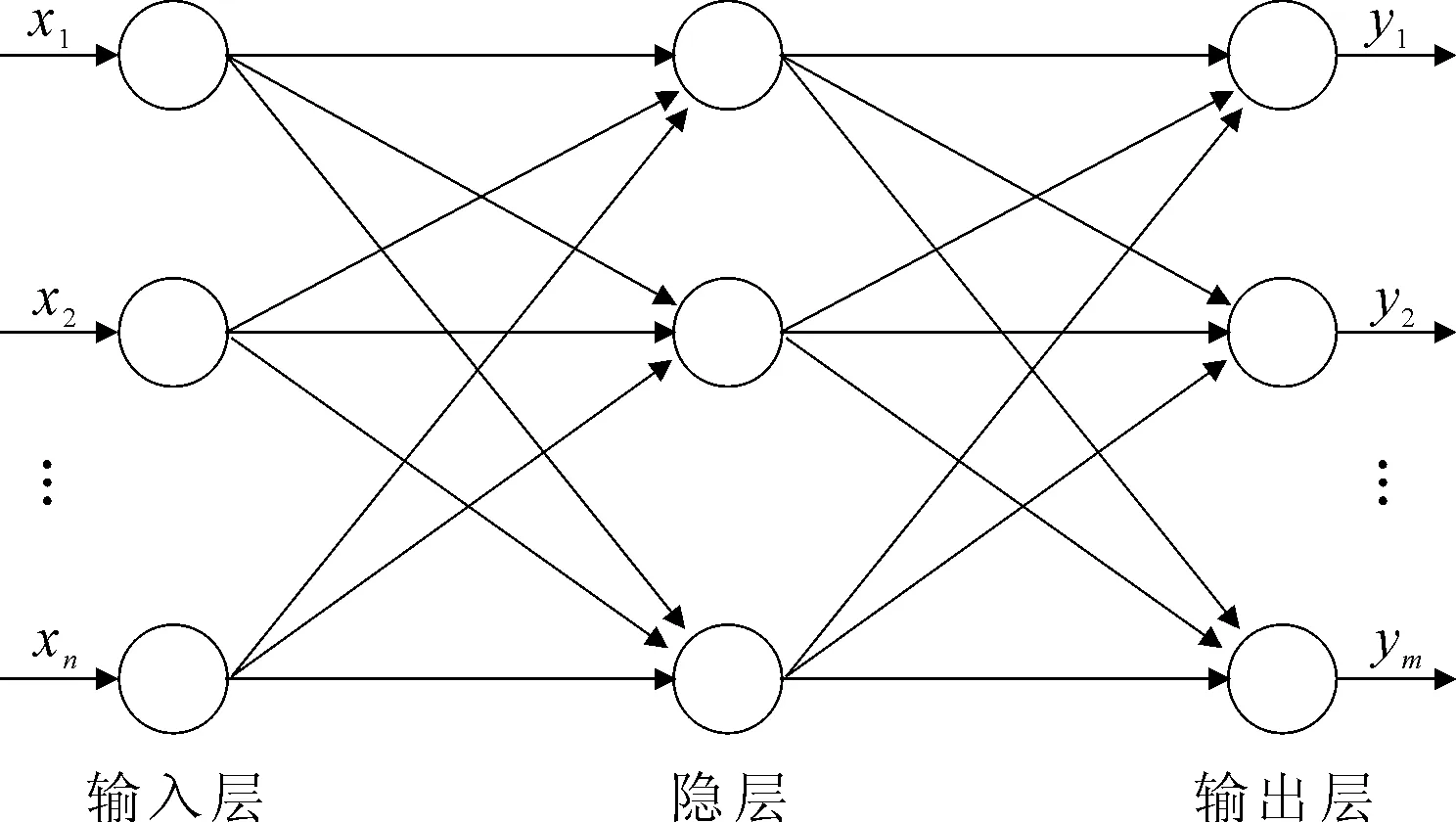
圖2　神經網絡的拓撲結構

RBF神經網絡由輸入層、隱層和輸出層3層結構組成。隱層神經元采用高斯函數作為傳遞函數，輸出層的傳遞函數是線性函數。陣元接收到信號后，先對信號進行預處理，即通過rxx1=E[xx1]和Rxx=E[xxH]分別求出參考信號和第2～M支路陣元信號的互相關矩陣，以及第2～M支路陣元上信號的自相關矩陣。RBF神經網絡可以處理的數據是實數，而通過陣列信號處理的rxx1和Rxx均為復數，因此需將它們拆分為實部與虛部分別作為RBF神經網絡的輸入，而RBF神經網絡的輸出則為逼近后的最佳權向量值。

2.2網絡學習

RBF神經網絡的學習[11]是在多維空間中尋找訓練數據的最佳擬合平面。假設陣列接收信號的角度θ的變化范圍為-90°到90°，取間隔為0.5°，則可以產生361對訓練樣本數據，訓練樣本數據的處理即是網絡的學習。基于RBF神經網絡的功率倒置波束形成算法的學習步驟如下。

步驟1根據不同信號的入射角度θ，求出陣列接收信號x和x1。

步驟2采用快拍數L和陣列的接收信號，求出信號的自相關矩陣Rxx=E[xxH]和信號與參考信號的互相關矩陣rxx1=E[xx1]，利用式(6)求出功率倒置的最佳權向量wopt。

步驟5得到網絡輸出，即為逼近后的功率倒置算法權向量的實部虛部Vre、Vim，并轉換為復數VRBF。

步驟6將VRBF與最佳權向量wopt進行比較，計算其誤差，如誤差大于給定誤差e，則跳回步驟1，否則進行步驟7。

步驟7停止循環運算，RBF網絡學習結束，確定隱層到輸出層連接權向量。

3仿真結果

通過MATLAB軟件進行算法有效性驗證。采用均勻直線陣列，陣元個數為4，陣元間距為1/2波長，采樣點數為1 000，對比本文算法與功率倒置算法的陣列響應方向圖。將窄帶信號作為信號源，從遠場入射。1個信號從0°入射，2個干擾信號分別從30°、-50°入射。陣列響應方向圖仿真比較如圖3所示。

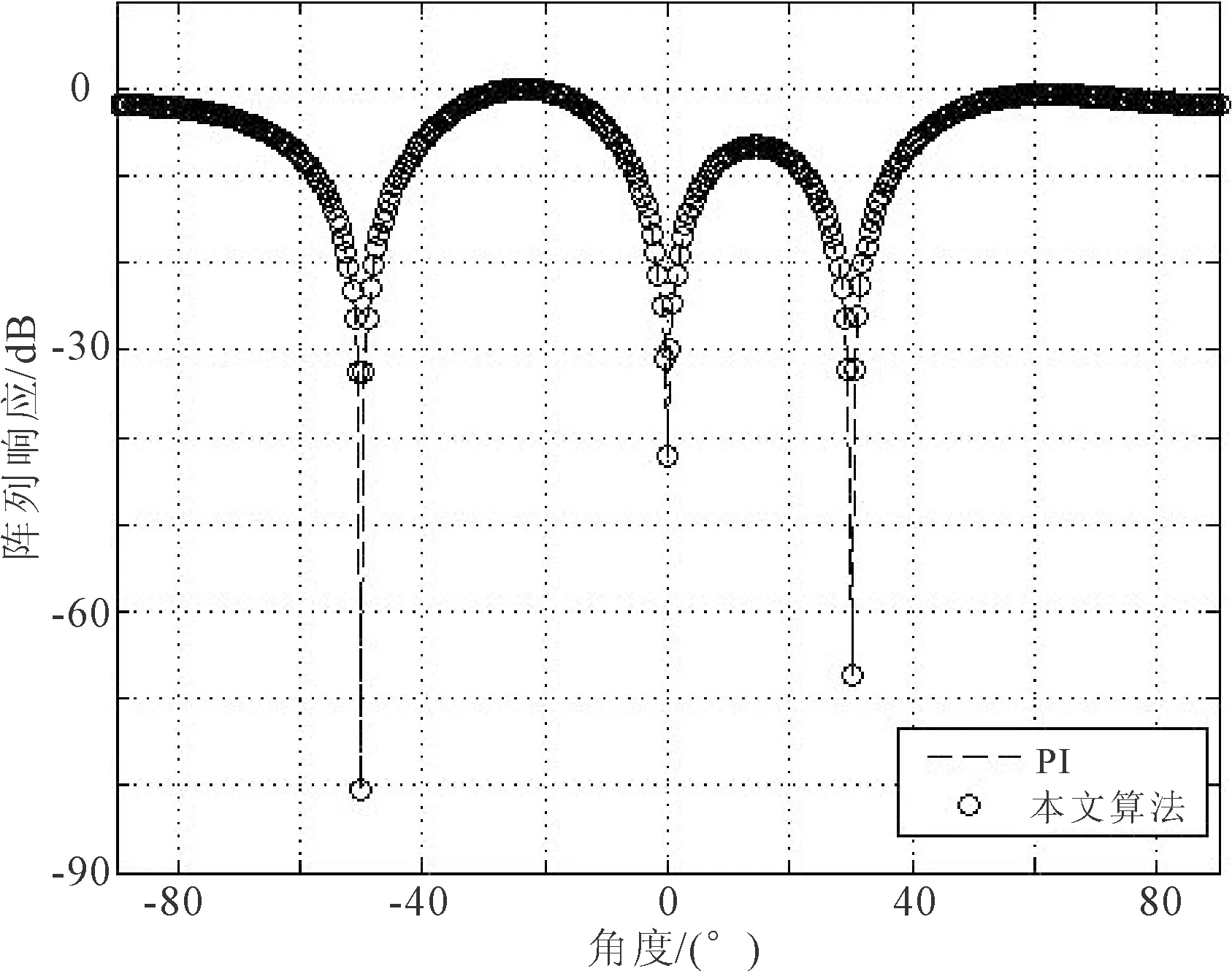
圖3　2個干擾信號陣列響應方向圖對比

從圖3中可以看出，兩種算法的陣列響應方向圖吻合的相當完好。由于功率倒置算法中不區分信號與干擾，因此在有不同方向的信號與干擾時，其方向圖在干擾與信號角度上均產生了零陷，強度愈強，產生的零陷愈深。

為了進一步驗證本文算法的有效性，在圖3仿真條件的基礎上，再進行1個期望信號和3個干擾信號的仿真。期望信號角度是0°，3個干擾信號角度分別是：30°，80°，-50°。陣列響應方向圖仿真比較如圖4所示。

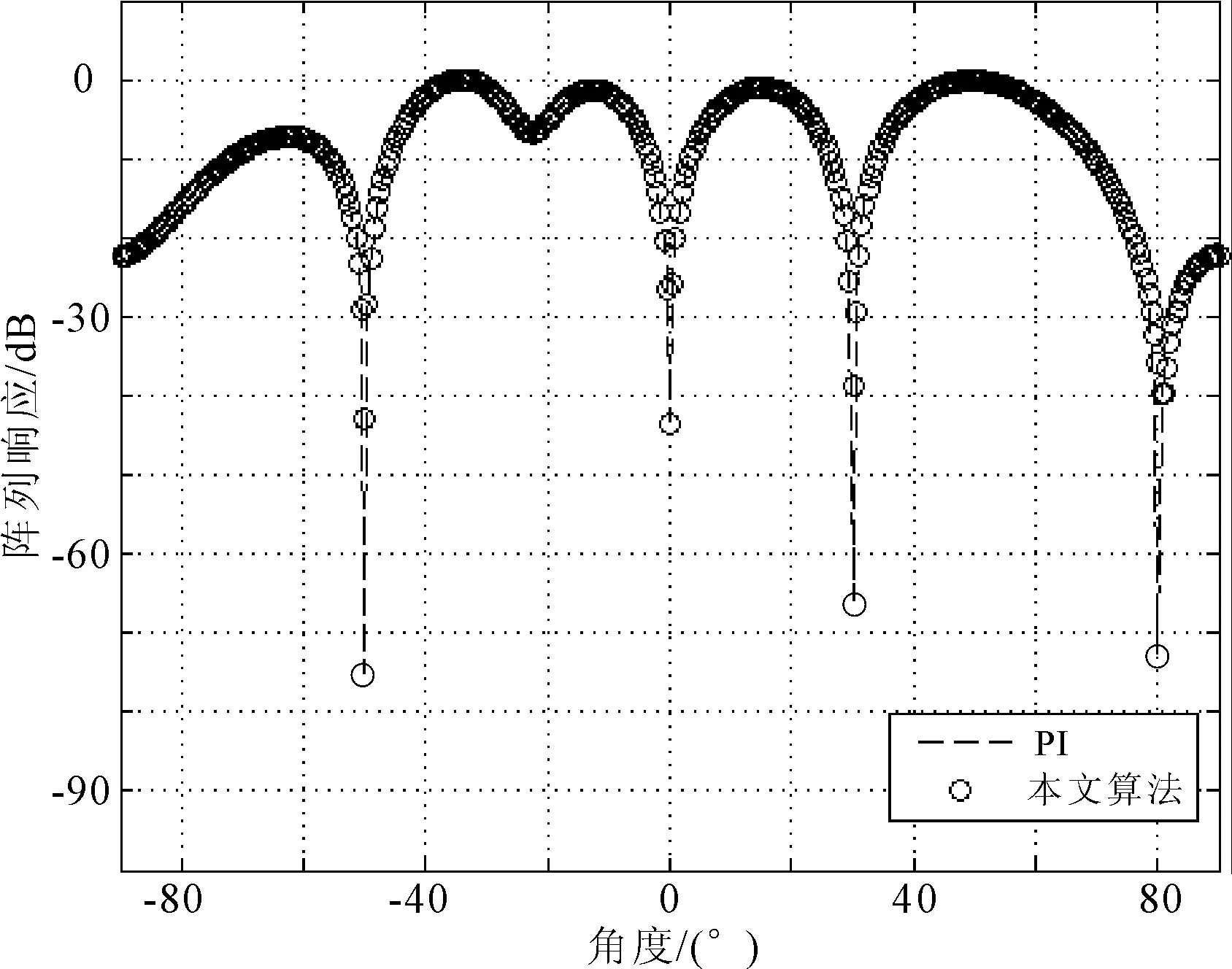
圖4　3個干擾信號陣列響應方向圖對比

從圖3和圖4中可以看出，當干擾信號個數增加，兩種算法的陣列響應方向圖依然吻合完好，進一步說明了算法的有效性。并且，本文算法實現時不需要復雜的矩陣之間運算，訓練好的網絡可以直接進行仿真，減少了算法運算量。為了驗證本文算法的逼近效果，定義陣列輸出響應的相對誤差為

其中GPI為功率倒置算法的陣列輸出響應，GRBF為本文算法的陣列輸出響應。圖5給出了陣列輸出響應相對誤差e的仿真圖形。

圖5　陣列輸出響應的相對誤差

圖5可見，陣列輸出響應的相對誤差一直是0，說明基于RBF神經網絡的功率倒置波束形成算法逼近效果好。

4結語

基于RBF神經網絡的功率倒置波束形成算法，在對RBF神經網絡進行訓練前，將網絡的輸入數據進行處理，減少了網絡訓練時間，將訓練好的網絡應用于功率倒置算法。仿真結果表明，本文算法可以快速逼近功率倒置算法的最佳權向量，有效地在干擾信號處產生零陷，并且運算量較小。

參考文獻

[1]韓英臣，趙興錄，趙國慶.自適應波束形成技術的發展與研究現狀[J].航天電子對抗，2008,25(2)：61-64.

[2]邱冬冬，金華松，孫永江.自適應波束形成算法的研究[J].電子設計工程，2013,21(1)：44-46.DOI:10.14022/j.cnki.dzsjgc.2013.01.026.

[3]YUL,LIUW,LangleyR.SINRAnalysisoftheSubtraction-BasedSMIBeamformer[J].IEEESignalProcessingSociety,2010,58(11):5926-5932.

[4]馬國棟,閆樹田,賀成柱,等.基于LMS算法與RLS算法自適應濾波及仿真分析[J].電子設計工程，2014,22(6):43-45.DOI:10.14022/j.cnki.dzsjgc.2014.06.027.

[5]仉智權，朱暢，馮起,等.功率倒置算法在北斗抗干擾天線系統中的應用[J].電子設計工程，2012,20(4):42-43.DOI:10.14022/j.cnki.dzsjgc.2012.04.021.

[6]SAVITHAR,VIGNESWARANS,SURESHS,etal.AdaptiveBeamformingusingComplex-valuedRadialBasisFunctionNeuralNetworks[C]//TENCON2009 -2009IEEERegion10Conference,Singapore:IEEE,2009:1-6.DOI:10.1109/TENCON.2009.5396002.

[7]張貞凱，田雨波，周建江.基于廣義回歸神經網絡集成的寬帶波束形成算法[J].宇航學報，2012,33(8)：1127-1131.

[8]呂翠改，成傳湘，陳國通,等.基于RLS與LMS算法的功率倒置陣列性能評估[J].西安郵電大學學報.2013,18(1):46-49.DOI:10.13682/j.issn.2095-6533.2013.01.010.

[9]袁暉坪.廣義酉矩陣與廣義Hermite矩陣[J].數學雜志，2003,23(3):375-380.

[10] 王爾馥，孟維曉，史兢.基于遺傳算法RBF網絡的波束形成[J].哈爾濱工業大學學報，2007,39(1)：89-92.

[11] 張寶軍，盧夢怡，陳治清,等.基于徑向基函數神經網絡的波束形成算法[J].西安郵電大學學報，2015,6(20)：33-36.DOI:10.13682/j.issn.2095-6533.2015.06.008.

[責任編輯:祝劍]

Powerinversionbeamformingalgorithm

basedonRBFneuralnetwork

ZHANGBaojun,YUANJie

(SchoolofElectronicEngineering,Xi’anUniversityofPostsandTelecommunications,Xi’an710121,China)

Abstract:A radial basis function neural network based power inversion algorithm was presented. This method calculates the two variables of optimal weight vector power in inversion algorithm, namely the autocorrelation matrix of received signal and the cross-correlation matrix of reference signal and the received signal. Then they are put into the RBF neural network, and the network is trained. In order to reduce the network training time, only the useful information of received signal autocorrelation matrix are extracted and input back into the network. This makes the best right vector approximation power inversion. Simulation results show that the proposed algorithm can accurately approximate power inversion of optimal weight vector and reduce the computational complexity.

Keywords:beamforming, power inversion, RBF neural networks

doi:10.13682/j.issn.2095-6533.2016.03.015

收稿日期：2015-12-24

基金項目：陜西省教育廳專項科研計劃資助項目(15JK1654)

作者簡介：張寶軍(1972-)，男，副教授，從事通信信號處理和無線定位研究。E-mail:zbj@xupt.edu.cn 袁潔(1989-)，女，碩士研究生，研究方向為電子與通信工程。E-mail:dangxia1314@163.com

中圖分類號：TN911.7

文獻標識碼：A

文章編號：2095-6533(2016)03-0090-04