槍托連續沖擊作用下的人體參數辨識

金鑫，周克棟，赫雷，黃雪鷹，張俊斌（.南京理工大學機械工程學院，江蘇南京0094；.63856部隊，吉林白城3700）

?

槍托連續沖擊作用下的人體參數辨識

金鑫1，周克棟1，赫雷1，黃雪鷹2，張俊斌2
（1.南京理工大學機械工程學院，江蘇南京210094；2.63856部隊，吉林白城137001）

摘要：針對槍托連續沖擊作用下人體系統參數隨時間變化的特點，提出了一種人體物理參數辨識方法。該方法通過正交化經驗模態分解和Hilbert變換構建輸入和輸出信號的解析信號。通過推導含參數變量的解析信號方程并計算求解獲得人體參數隨時間的變化曲線。表面肌電實驗結果證明了該方法的有效性。辨識結果表明，該方法獲得的連續沖擊作用下人體等效剛度和等效阻尼參數曲線與生物學知識相符，具有重要意義。

關鍵詞：兵器科學與技術；參數辨識；生物力學；時變系統；正交化經驗模態分解；連續沖擊

周克棟（1964—），男，教授，博士生導師。E-mail：zkd81151@126. com

0 引言

如何定量地描述沖擊作用下的人體系統是一個十分困難的問題。文獻［1］通過Kane方法，建立了人體系統和施力物體（武器）的動力學方程，利用試驗測試數據計算獲得了人體相關參數。文獻［2］采用類似方法，通過第二類Lagrange方程建立動力學模型。文獻［3］通過機械導納方法，辨識獲得人體肩部的模態及物理參數。然而，上述工作均存在一個潛在的假設，即人體物理參數是一個恒定的值，不隨時間的變化而變化。

實際情況下，人體系統應該屬于時變系統。尤其是當人體受到連續沖擊作用時，人體系統物理參數明顯存在隨時間而變化的現象。根據生物學研究［4］可知，神經系統響應時間約為150～200 ms，而肌肉響應時間則在200 ms左右。因此，當沖擊開始一段時間后，人體肌肉發生力的作用，宏觀上表現為人體系統的物理參數隨時間發生變化。

本文以人體立姿持槍連續射擊為例，分析了在武器后坐力作用下人體系統的物理參數特性，提出了人體參數的辨識方法。該方法通過正交化經驗模態分解（OEMD）和Hilbert變換構建解析信號，通過推導含參數變量的解析信號方程并計算獲得人體參數隨時間的變化曲線。通過射手表面肌電測量實驗驗證了方法的可靠性。實際射擊試驗的辨識結果亦符合生物學常識。

1 人體參數辨識方法

經驗模態分解（EMD）自提出以來，被廣泛應用于各類信號處理領域［5 -6］。然而，信號經EMD處理得到的內在模態函數（IMF）分量并不存在嚴格的正交性。大量實踐［7］表明，EMD方法的正交性指標IO一般在10-2～10-3數量級，這樣的近似正交性會導致信號經EMD分解產生不可知的能量泄露。因此，有學者基于EMD方法提出了OEMD方法［8］。

1. 1 OEMD方法

EMD方法在信號處理領域廣為人知，因此不做贅述。本文在此主要對OEMD方法進行描述。OEMD方法的核心思想是對EMD處理得到的各階IMF分量進行正交化處理。其具體過程如下：

2）令r1（t）= x（t）-（t）作為新信號進行EMD分解，得到第2階初始IMF分量（t）.為了得到與c1（t）嚴格正交的第2階正交化IMF分量c2（t），從（t）中去除含有c1（t）的分量為

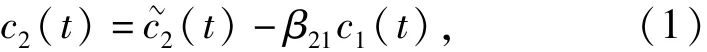
式中：β21為（t）和c1（t）之間的正交化系數。其離散形式下的表達式為

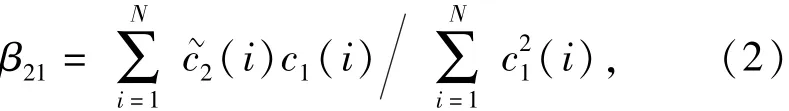
式中：N為信號長度。

3）將rj（t）= rj -1（t）-（t），j≥2作為新信號進行EMD處理，得到第j +1階初始IMF分量（t）.從中去除前j階正交化IMF分量，得到第j +1階正交化IMF分量為

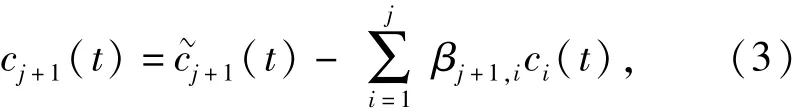
式中：正交化系數βj +1，i的離散形式表達式為

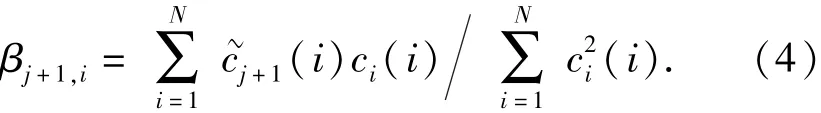
4）重復上述過程，直至rn（t）滿足EMD終止條件，OEMD處理過程結束。原始信號x（t）最終表示為

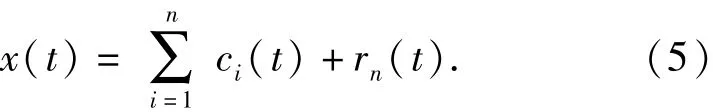
1. 2 解析方程

為了方便分析，假設人體在受到連續沖擊作用時各自由度方向運動相對獨立，且人體上半身作為同一剛體不發生較大變形［9］。人體在俯仰方向的運動微分方程可表示為

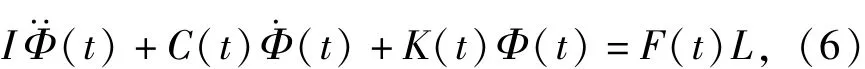
式中：I為人體上半身在俯仰方向的轉動慣量；F（t）為作用于人體的連續沖擊激勵；Φ（t）為俯仰方向的角位移響應；C（t）和K（t）分別為人體隨時間變化的廣義等效阻尼與等效剛度。

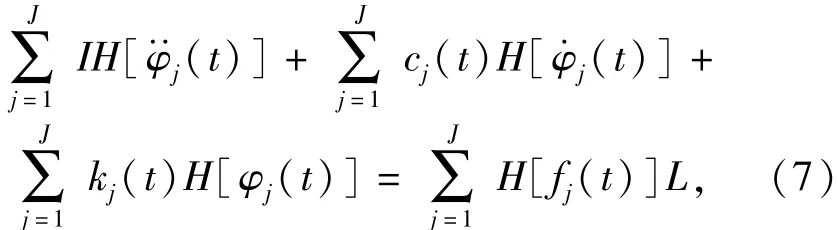
式中：

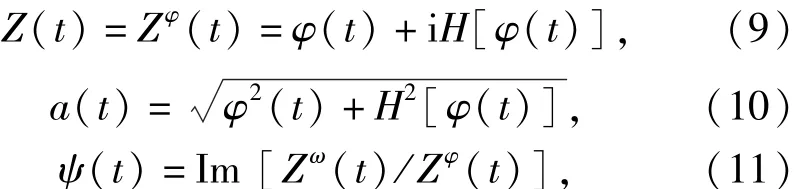
Z（t）表示信號φ（t）的解析信號（ZF（t）的求法同理），a（t）和ψ（t）分別表示解析信號的幅值函數和相位函數。（t）表示信號（t）的解析信號。

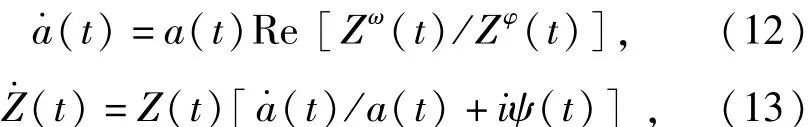
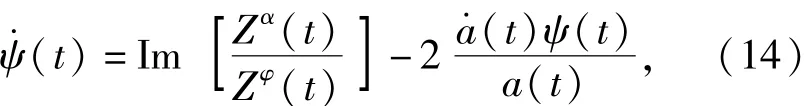
綜上所述，識別人體系統阻尼C（t）和剛度K（t）的過程［10 -15］如下：

步驟1 將人體系統在俯仰自由度方向的角位移、角速度、角加速度響應信號以及沖擊作用激勵信號分別做OEMD處理，獲得：φj（t）、（t）、（t）以及fj（t），根據（9）式分別構造相應的解析信號：（t）、（t）、（t）以及（t）.

步驟3 對整個時間長度t為0～T重復上述過程，即可獲得人體系統阻尼和剛度隨時間的變化曲線C（t）和K（t）.

2 試驗及辨識結果

本文以立姿無依托持槍連續射擊情況下的人體作為研究對象，以95-1式自動步槍作為試驗用槍，進行了參數辨識試驗。試驗采用美國Dytran-1050C型壓電式力傳感器測試武器沖擊作用力，采用XSENS MTi-10型陀螺儀測試人體在沖擊作用下的動態響應。試驗照片如圖1所示。試驗重復多次，一致性較好。選取其中一次5發連續射擊試驗的俯仰自由度方向數據進行參數辨識。本文同樣對人體的扭轉和收展自由度方向進行了辨識，結果與俯仰自由度方向結果類似。但由于后文肌肉電信號試驗中無法從生物學知識中明確知曉影響扭轉和收展自由度方向等效阻尼和等效剛度的肌肉位置，故而無法有效證明辨識結果。因此，本文僅對俯仰自由度方向進行討論。

試驗獲得的輸入激勵如圖2（a）所示，獲得的輸出角加速度、角速度和角位移響應曲線分別如圖2（b）、圖2（c）和圖2（d）所示。

辨識過程中，由國家標準GB 1000—88“中國成年人人體尺寸”可知，人體轉動慣量I =0.283 977 kg·m2，同時測量可得沖擊作用力的力臂L =0. 692 m.對輸入和輸出信號進行一定的處理以消除零值偏差帶來的影響，即保證射擊開始前F（t）和Φ（t）等值均為0.人體系統俯仰自由度方向剛度和阻尼的辨識結果分別如圖3（a）和圖3（b）所示。

圖1 射擊試驗照片Fig. 1 Photo of shooting experiment

值得注意的是，圖3中辨識結果的等效剛度和等效阻尼為廣義的等效剛度和等效阻尼參數，其幅值的物理意義為：已知剛度/阻尼的幅值為相應的力與角位移/角速度的比值。如果在t時刻系統的瞬時力與瞬時角位移/角速度方向相反，則此時系統的瞬時剛度/阻尼值為負，反之為正。

由圖2已知射擊開始于0. 2 s時刻，結束于0. 7 s時刻前后，對應圖3中0. 2 s時刻前后人體系統的等效剛度和等效阻尼開始發生變化，在0. 7 s時刻前后基本結束變化。其中，圖3（a）表明人體系統的等效剛度于0. 38 s時刻前后發生極大的突變，因為此時人體腹部肌肉在控制神經作用下用力產生彈性剛度導致角位移變化突然減小，宏觀反映為人體等效剛度的突然增大。人體系統等效剛度在達到第一個極大值后一段時間內恢復到零值附近，其后又于0.55 s時刻前后（第一次后約0.2 s）達到第二個極大值，表明人體腹部肌肉通過彈性剛度對射擊姿態的調整作用是分段的，而非連續的。

同樣，圖3（b）表明，人體系統的等效阻尼在0. 4 s時刻前后有一次較為明顯的波動變化，而后在0. 55 s時刻前后達到突變的最大值，反應了人體腰部肌肉在此過程中產生力的作用，以彈性阻尼的形式阻礙人體產生較大的角位移變化。人體系統的等效剛度和等效阻尼的變化趨勢與生物學人體肌肉響應時間200 ms基本相符。整個射擊過程人體肌肉作用方式與經驗射手的主觀感覺相符。

3 試驗驗證

為了證明表示結果的可靠性，本文進行了連續射擊情況下人體肌肉的表面肌電信號（sEMG）測量試驗，如圖4所示。試驗測量了射擊過程中射手腰部后側肌肉和腹部肌肉的sEMG信號，分別如圖5（a）和5（b）所示。

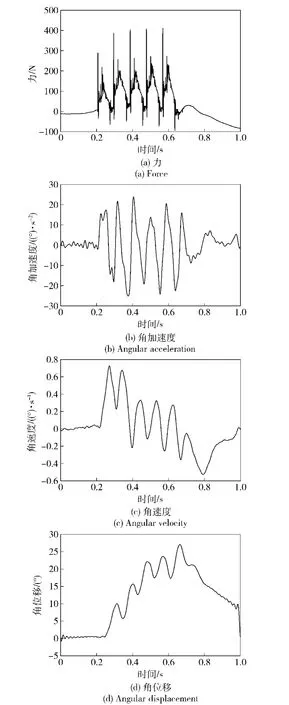
圖2 輸入激勵和輸出響應曲線Fig. 2 Curves of input force，output angle，angular velocity and angular acceleration

試驗觀察可以發現，射手腰部后側肌肉sEMG信號與人體剛度辨識結果，以及腹部肌肉sEMG信號與人體阻尼辨識結果，有著類似的變化趨勢。同時幅值明顯的極大值點對應出現在0. 38 s和0. 55 s附近，具有良好的一致性。生物力學分析認為［16］，人體等效剛度和阻尼與肌肉力間存在內在的因果聯系。文獻［17］認為：腹部肌肉主要用于降低軀體對載荷響應的頻率和振幅，這與阻尼器的效果近似；而腰部豎脊肌的作用在于增加軀干緊張度，這與彈簧的效果近似。因此，辨識結果與sEMG信號近似是有其生物力學內因的，本文辨識方法亦是有效且可靠的。

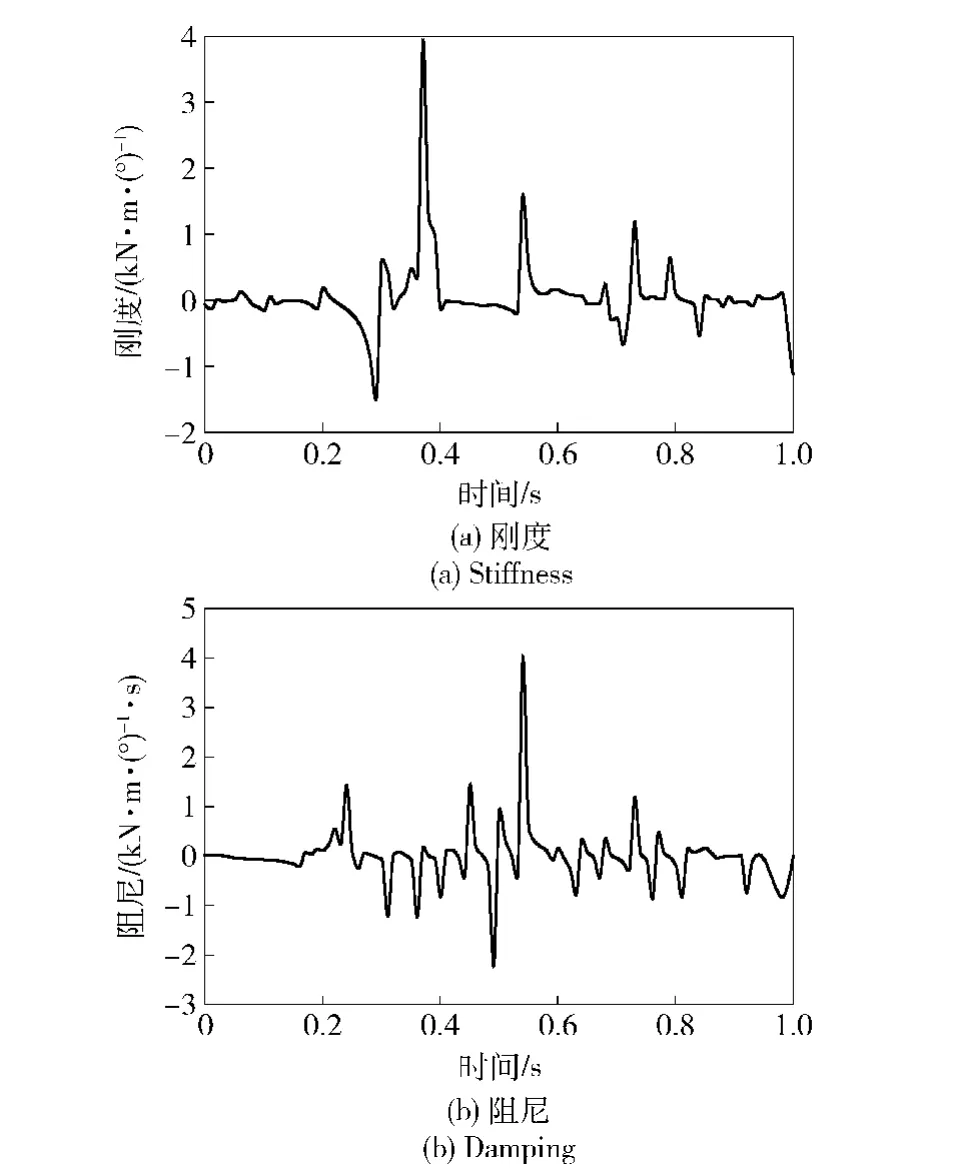
圖3 人體阻尼和剛度辨識結果Fig. 3 Identification results of human damping and stiffness

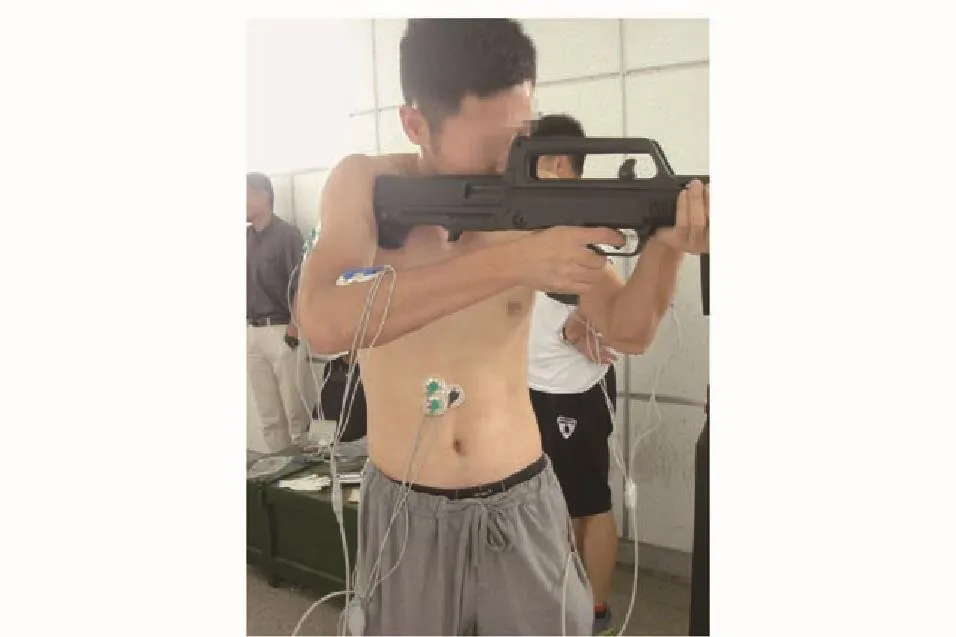
圖4 人體肌肉的表面肌電信號測量試驗照片Fig. 4 Photo of shooter muscles sEMG measurement

4 結論

1）本文提出了基于OEMD方法的人體時變參數辨識方法。辨識結果表明，射擊過程中人體的等效阻尼和等效剛度參數不是一個恒定值，而是一個隨時間變化的參數。射擊過程中人-槍系統為一個時變系統。

圖5 射手表面肌電信號測量結果Fig. 5 Results of shooter muscles sEMG measurement

2）辨識獲得的人體等效阻尼和等效剛度時變參數可用于求解人-槍模型的動力學方程系數，使得現有多自由度、多剛體人-槍模型適用于連續射擊情況。

3）本文所提方法對分析人體在其他受力情況下的時變參數辨識具有參考價值，因此本文方法具有一定普適意義。

4）基于真實試驗數據進行了人體阻尼和剛度的參數辨識，辨識結果對自動武器及相關領域的設計研究具有參考意義。

參考文獻（References）

［1］ 李永新，朱明武，孫海波，等.人槍系統動力響應研究［J］.兵工學報，1999，20（1）：8 -12. LI Yong-xin，ZHU Ming-wu，SUN Hai-bo，et al. Dynamic research of man-weapon system［J］. Acta Armamentarii，1999，20（1）：8 -12.（in Chinese）

［2］ 包建東，王昌明，何云峰.人-槍模型的建立及仿真分析［J］.兵工學報，2009，30（5）：513 -517. BAO Jian-dong，WANG Chang-ming，HE Yun-feng. Foundation of man-gun model and simulation analysis［J］. Acta Armamentarii，2009，30（5）：513 -517.（in Chinese）

［3］ 孔德仁，孫海波，李永新，等.槍肩系統機構導納分析［J］.南京理工大學學報，1997，21（5）：441 -444. KONG De-ren，SUN Hai-bo，LI Yong-xin，et al. Mechanical admittance analysis of rifle-shoulder system［J］. Journal of Nanjing University of Science and Technology，1997，21（5）：441 - 444. （in Chinese）

［4］ 王亞平，徐誠，郭凱.人槍系統建模及數值仿真研究［J］.兵工學報，2002，23（4）：551 -554. WANG Ya-ping，XU Cheng，GUO Kai. Modeling and digital-simulation of a human-gun system［J］. Acta Armamentarii，2002，23（4）：551 -554.（in Chinese）

［5］ Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］. Proceedings of the Royal Society A-Mathematical Physical and Engineering Sciences，1998，454（1971）：903 -995.

［6］ 李鴻光，孟光.基于EMD方法的混沌信號中周期分量的提取［J］.應用數學和力學，2006，27（2）：199 -203. LI Hong-guang，MENG Guang. Harmonic component extraction from a chaotic signal based on EMD method［J］. Applied Mathematics and Mechanics，2006，27（2）：199 -203.（in Chinese）

［7］ Huang N E，Shen Z，Long S R. A new view of nonlinear water waves：the Hilbert spectrum［J］. Annual Review of Fluid Mechanics，1999，31（1）：417 -457.

［8］ 樓夢麟，黃天立.正交化經驗模式分解方法［J］.同濟大學學報：自然科學版，2007，35（3）：293 -298. LOU Meng-lin，HUANG Tian-li. Orthogonal empirical mode decomposition［J］. Journal of Tongji University：Natural Science，2007，35（3）：293 -298.（in Chinese）

［9］ 胡敬坤.輕武器射擊平臺的初步研究［D］.南京：南京理工大學，2007. HU Jing-kun. Preliminary research of small arms firing platform ［D］. Nanjing：Nanjing University of Science and Technology，2007.（in Chinese）

［10］ 徐晴晴.基于改進經驗模態分解的線性系統參數識別問題研究［D］.南京：南京航空航天大學，2013. XU Qing-qing. Parameters identification for linear structures based on an improved EMD method［D］. Nanjing：Nanjing University of Aeronautics and Astronautics，2013.（in Chinese）

［11］ Liu K. Identification of linear time-varying systems［J］. Journal of Sound and Vibration，1997，206（4）：487 -505.

［12］ Yang J N，Lei Y，Pan S，et al. System identification of linear structures based on Hilbert Huang spectral analysis. Part 1：normal modes［J］. Earthquake Engineering and Structural Dynamics，2003，32（10）：1443 -1465.

［13］ Shi Z Y，Law S S. Identification of linear time-varying dynamical systems using Hilbert transform and empirical mode decomposition method［J］. Journal of Applied Mechanics，2007，74（2）：223 -230.

［14］ Cohen L. Time-frequency analysis：theory and applications ［M］. New York：Prentice Hall，1995.

［15］ T?zeren A. Human body dynamics：classical mechanics and human movement［M］. New York：Springer-Verlag，1999.

［16］ Panjabi M M. The stabilizing system of the spine. Part I：function，dysfunction，adaptation and enhancement［J］. Journal of Spinal Disorders，2015，5（4）：383 -397.

［17］ Vera-Garcia F J，Brown S H，Gray J R，et al. Effects of different levels of torso co-activation on trunk muscular and kinematic responses to posteriorly applied sudden loads［J］. Clinical Biomechanics，2006，21（5）：443 -455.

Parameter Identification of Human Body under Successive Impact

JIN Xin1，ZHOU Ke-dong1，HE Lei1，HUANG Xue-ying2，ZHANG Jun-bin2
（1. School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China；2. 63856 Unit of PLA，Baicheng 137001，Jilin，China）

Abstract：A parameter identification method of human body under successive impact is proposed，considering the variation of the parameters over time. Orthogonal empirical mode decomposition（OEMD）and Hilbert transform are used in the method to build the analytic signals of input and output signals. The equation of analytic signals with variable parameters is derived，and the human body parameters changing with time are calculated. Surface electromyography experimental results show that the proposed method is effective. Identification result shows that the equivalent stiffness and equivalent damping parameters of human body under successive impact obtained in this paper are consistent with biology.

Key words：ordnance science and technology；parameter identification；biodynamics；time-varying system；orthogonal empirical mode decomposition；successive impact

中圖分類號：O32

文獻標志碼：A

文章編號：1000-1093（2016）04-0598-05

DOI：10. 3969/ j. issn. 1000-1093. 2016. 04. 004

收稿日期：2015-08-05

基金項目：總裝備部31基地技術研究項目（2014年）

作者簡介：金鑫（1987—），男，博士研究生。E-mail：jay12337@ hotmail. com；