基于循環(huán)平穩(wěn)度準則的多路雷達信號識別算法
王紅衛(wèi),范翔宇,陳游,楊遠志(.西北工業(yè)大學(xué)電子信息學(xué)院,陜西西安7007;.空軍工程大學(xué)航空航天工程學(xué)院,陜西西安70038)
?
基于循環(huán)平穩(wěn)度準則的多路雷達信號識別算法
王紅衛(wèi)1,范翔宇2,陳游2,楊遠志2
(1.西北工業(yè)大學(xué)電子信息學(xué)院,陜西西安710072;2.空軍工程大學(xué)航空航天工程學(xué)院,陜西西安710038)
摘要:在日益復(fù)雜的電磁環(huán)境中分選識別出雷達信號,是電子對抗發(fā)揮功用的先決因素。關(guān)于雷達信號調(diào)制樣式與信號參數(shù)的先驗信息有限,難以為信號分選提供充足的情報支撐,且信號交疊嚴重制約著信號分選的效能。將上述需求轉(zhuǎn)換為盲源分離問題,通過Givens變換構(gòu)造高階分離矩陣,將適用于兩路信號的基于3階循環(huán)量的循環(huán)平穩(wěn)度(DCS)盲源分離算法拓展到適用于具有不同循環(huán)平穩(wěn)頻率的多路信號。通過理論推導(dǎo)證明了該方法的可行性,并推導(dǎo)出構(gòu)造Givens矩陣參數(shù)確定的方法。利用循環(huán)平穩(wěn)理論提取雷達信號在循環(huán)平穩(wěn)域的特征,結(jié)合DCS分離準則進行仿真驗證。仿真結(jié)果表明,該算法能夠?qū)崿F(xiàn)對多路雷達信號的有效分選。
關(guān)鍵詞:雷達工程;信號識別;循環(huán)平穩(wěn)頻率;Givens矩陣;循環(huán)平穩(wěn)度盲源分離算法;多路信號
范翔宇(1991—),男,碩士研究生。E-mail:panda0077@163. com
0 引言
雷達輻射源識別是雷達電子戰(zhàn)中確定雷達類型的關(guān)鍵要素。基于偵收的信號進行輻射源識別已經(jīng)在民用與軍事方面引起廣泛關(guān)注,但傳統(tǒng)的技術(shù)難以應(yīng)對日益復(fù)雜與增長的雷達信號樣式[1 -3]。
現(xiàn)今在雷達輻射源識別方面已經(jīng)有了諸多的研究成果。許多輻射源識別算法以人工神經(jīng)網(wǎng)絡(luò)相關(guān)算法為核心[4 -5]。隨著研究的不斷深入,此類算法的識別精度逐漸提升。但是,基于神經(jīng)網(wǎng)絡(luò)的識別算法對樣本的準確性要求較高,且計算時間較長,難以保證實時性。文獻[6]采用模糊向量的方法,實現(xiàn)了對特定輻射源較好的識別,可基于模糊理論的算法自身主觀性過強,部分參數(shù)一旦設(shè)定就難以改變,通用性和更新能力較弱。文獻[7 -8]基于粗糙集理論實現(xiàn)對輻射源的識別,算法簡單,實時性強,可所偵收的信號一旦不在識別規(guī)則內(nèi),就難以實現(xiàn)輻射源的識別。文獻[9 -10]中提出的灰色關(guān)聯(lián)度方法能夠提高低信噪比條件下對雷達輻射源的識別率,但是灰色系統(tǒng)中權(quán)重通常是根據(jù)應(yīng)用經(jīng)驗主觀賦值,缺乏理論依據(jù),在復(fù)雜的數(shù)據(jù)環(huán)境下可靠性有待商榷。文獻[11]中采用隸屬度函數(shù)解決了識別中的不確定性,而隸屬度函數(shù)的選取與主觀因素關(guān)聯(lián)較大。文獻[12 - 13]采用D-S理論實現(xiàn)對輻射源的識別,采用邏輯推理的方式實現(xiàn)信號的識別,可其計算量較大,難以兼顧實時性與準確性。
上述方法將其他學(xué)科的研究成果引入到雷達輻射源識別中,取得了很好的效果。基于數(shù)據(jù)級的處理,易于實現(xiàn)且實時性較好,不過數(shù)據(jù)級屬于二次處理,信息的簡化導(dǎo)致部分細節(jié)信息丟失。因此,本文從偵察得到的具有全部原始信息的全脈沖樣本入手,深入到信號層面,結(jié)合信號自身的特征,利用循環(huán)平穩(wěn)理論的3階循環(huán)平穩(wěn)度(DCS)準則實現(xiàn)對雷達信號的分離。
循環(huán)平穩(wěn)理論是非平穩(wěn)信號的研究與應(yīng)用領(lǐng)域中一種具有鮮明特性的研究方法,其研究對象是統(tǒng)計特性為時間上的周期函數(shù)的一大類非平穩(wěn)信號。從功率譜的結(jié)構(gòu)上來看,循環(huán)平穩(wěn)信號統(tǒng)計特性的周期性使這類信號都具有譜相關(guān)性[14],這使得將循環(huán)平穩(wěn)信號與其他非循環(huán)平穩(wěn)信號分離較為容易,且絕大多數(shù)的雷達與通信信號均具有循環(huán)平穩(wěn)特性。其他的非平穩(wěn)信號的時變統(tǒng)計量必須要用信號的多次觀測記錄來進行估計,循環(huán)平穩(wěn)量卻可以從信號的單次觀測中估計得到。循環(huán)累積量可以抑制任何平穩(wěn)的有色噪聲,具有良好的抗噪性能。利用信號的低階循環(huán)統(tǒng)計量就可以達到良好的分離效果,具有較少的計算量,保證實時性。
1 循環(huán)平穩(wěn)的基本概念
1. 1 循環(huán)平穩(wěn)信號的定義
如果信號s(t)的1階和2階統(tǒng)計特性隨時間變化呈現(xiàn)出一定的周期性,則稱為廣義平穩(wěn)信號,即s(t)的均值與自相關(guān)函數(shù)滿足如下條件[15 -16]:
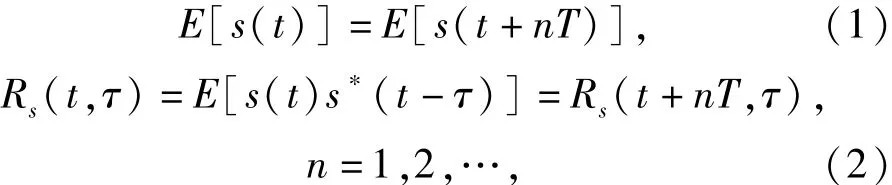
式中:1/ T為循環(huán)頻率,記為α.
因為自相關(guān)函數(shù)是周期函數(shù),因此可將其展開成傅里葉級數(shù),即
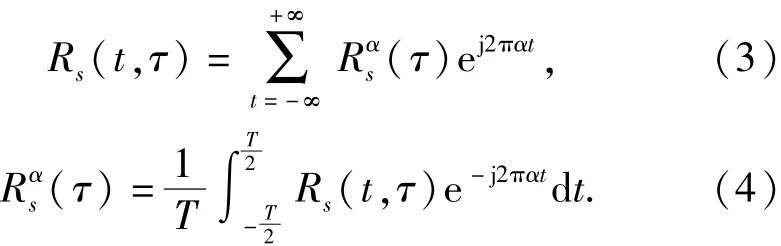
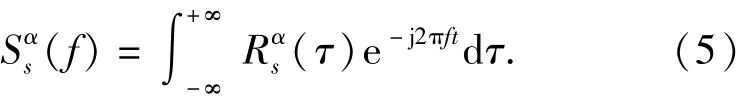
如果循環(huán)平穩(wěn)過程滿足周期遍歷性,則可用時變統(tǒng)計量代替循環(huán)統(tǒng)計量,從而得到
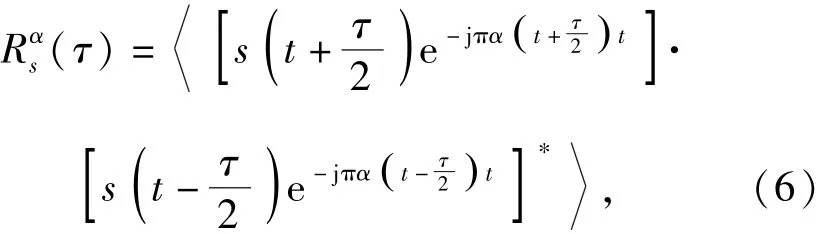
令
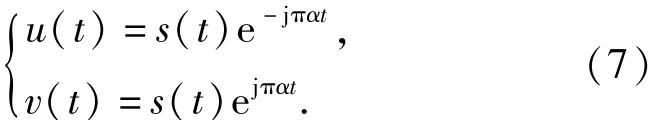
將(6)式進行改寫可以得到
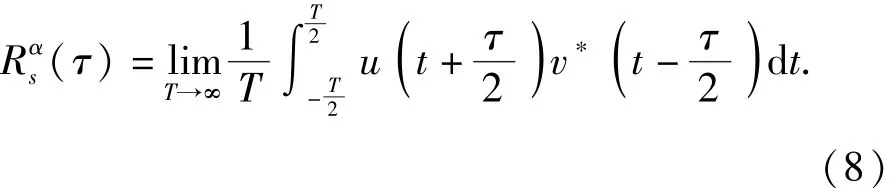
對(8)式進行傅里葉變換,得到
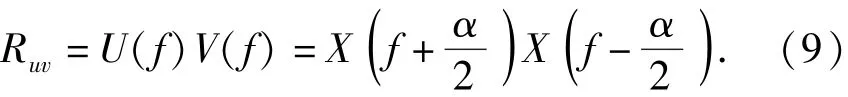
(8)式描述的是u(t)和υ(t)的卷積,(9)式將其轉(zhuǎn)換到頻域,得到U(f)和V(f)的乘積。通過(8)式、(9)式與卷積的性質(zhì)可以得到循環(huán)譜密度函數(shù)反映循環(huán)平穩(wěn)信號s(t)在頻率f±α/2處的相關(guān)程度,即循環(huán)譜密度是對循環(huán)平穩(wěn)信號譜相關(guān)程度的描述。絕大多數(shù)雷達信號均具有循環(huán)平穩(wěn)特性。本文基于此特征構(gòu)建數(shù)學(xué)模型,實現(xiàn)對混疊信號中的雷達信號分離提取。
1. 2 循環(huán)平穩(wěn)隨機過程的高階循環(huán)累積量
循環(huán)平穩(wěn)的隨機過程x(t)的高階累積量用符號[17]表示為
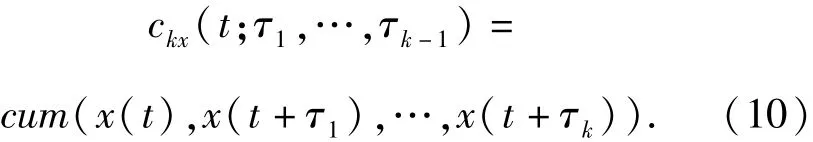
對于固定的滯后τ1,…,τk -1,如果ckx(t:τ)存在一個相對于t的傅里葉級數(shù)展開,則
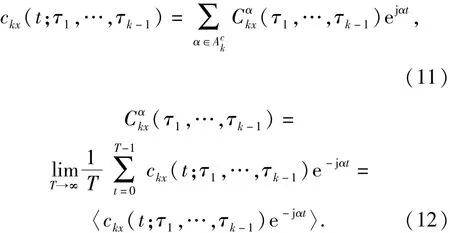
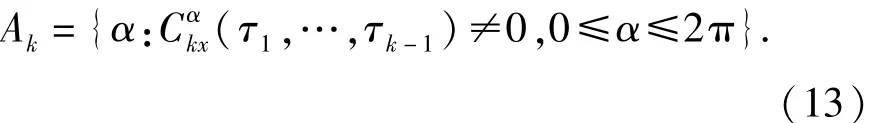
2 基于3階循環(huán)統(tǒng)計量的DCS雷達信號提取算法
2. 1 DCS的定義
DCS是用來度量信號在循環(huán)平穩(wěn)頻率α處的循環(huán)平穩(wěn)程度。連續(xù)信號的3階循環(huán)平穩(wěn)度定義[17]為
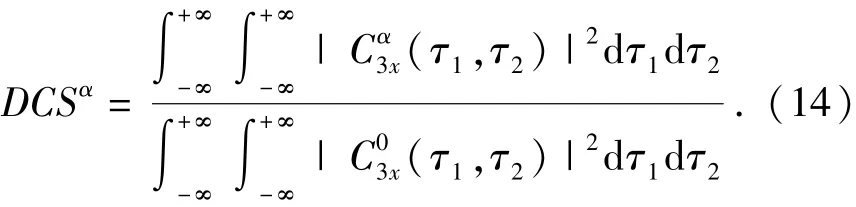
DCSα的值界于[0,1].當α≠0時,DCSα的值越大,反映信號在此循環(huán)頻率處的DCS越強。
2. 2 DCS分離準則
由于多數(shù)雷達信號在發(fā)送端經(jīng)過調(diào)制之后具有循環(huán)平穩(wěn)特性,而在空間中疊加的噪聲不具有循環(huán)平穩(wěn)特性。因此,可以基于DCS實現(xiàn)對雷達信號的提取。
定義目標函數(shù)G,令
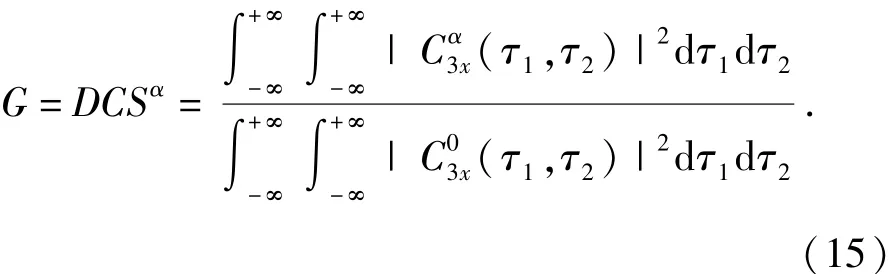
以G作為分離準則,可以采用智能算法使G為極大值,得到對應(yīng)的參數(shù)構(gòu)造分離矩陣,即可分離出混疊在接收信號中的雷達信號。
2. 3 分離模型
由于空間中的信號數(shù)量極多,易于與雷達信號發(fā)生混疊,使電子對抗方對其偵察的難度大幅度上升,因此要求根據(jù)傳感器偵收到的若干混合信號恢復(fù)出原始信號。具體模型如圖1所示[18 -19]。

圖1 基于3階DCS的雷達信號分選算法Fig. 1 The sorting algorithm of radar signals based on third-order DCS
圖1中s(t)為信號源,A為混合矩陣,B為本文要構(gòu)造的分離矩陣。將通過B輸出的分離信號s'(t)調(diào)節(jié)3階DCS準則,實現(xiàn)對B的修正,從而實現(xiàn)對G的最大值輸出。
3 算法可行性分析
令分離矩陣B為旋轉(zhuǎn)矩陣,由Givens變換的性質(zhì)可知,存在有限個Givens的矩陣乘積T,使T與矩陣的乘積為對角矩陣。而盲源分離的理想結(jié)果是混合信號與分離矩陣相乘后得到的結(jié)果為經(jīng)過初等變換的數(shù)乘單位矩陣。二者得到的結(jié)果相似,因而本文采用Givens變換矩陣構(gòu)造分離矩陣B.
本文以分離3路信號為研究重點,因而需要構(gòu)造兩組Givens變換,二者的乘積即為分離矩陣。根據(jù)Givens矩陣的性質(zhì),矩陣內(nèi)待求解的參量平方和為1,進而采用三角函數(shù)形式表示待求解參量,得到待求解的Givens矩陣的形式為
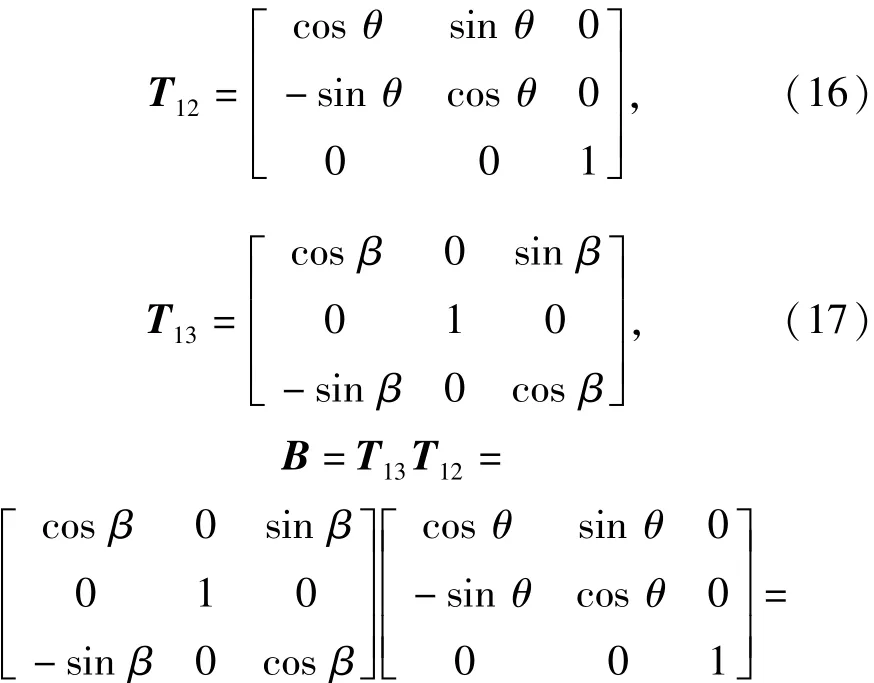
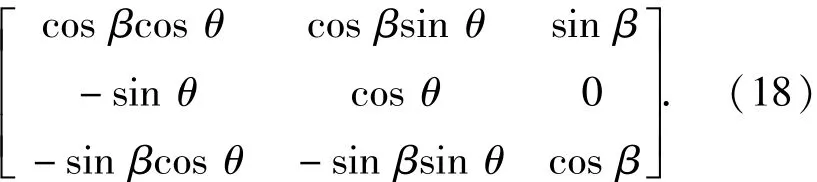
設(shè)混合矩陣A為
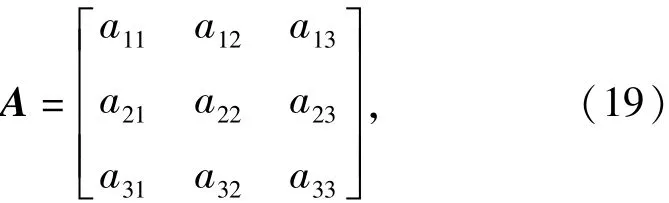
于是輸出信號s'(t)為
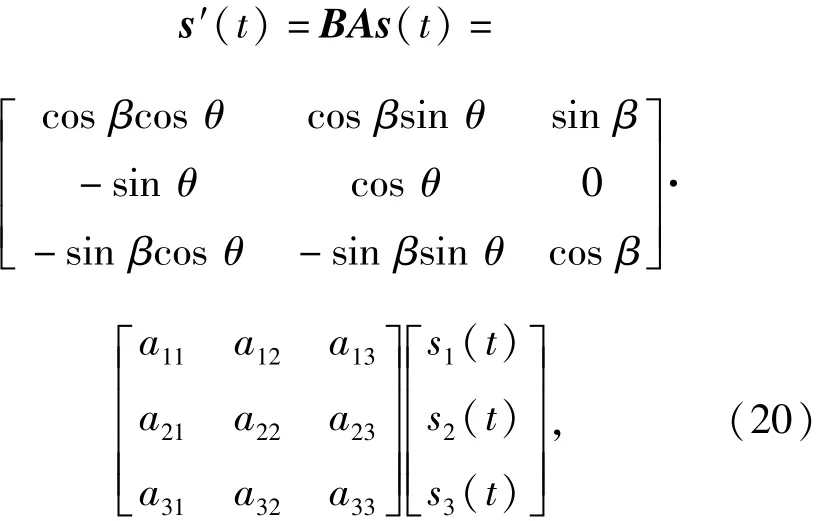
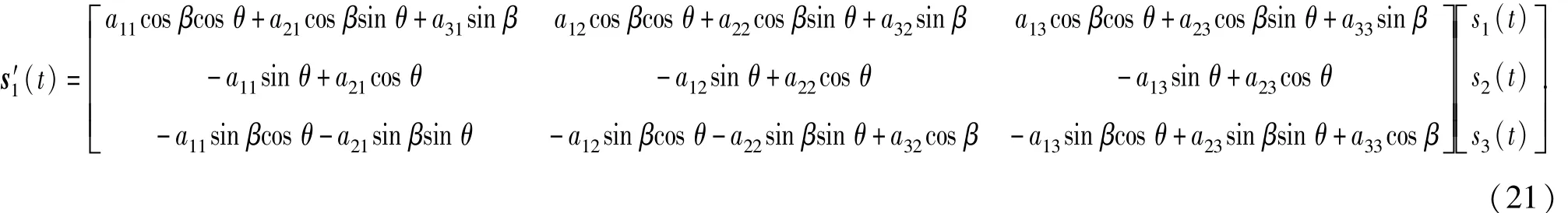
取出其中一路信號s'1(t)進行分析論證。由于全局函數(shù)為關(guān)于θ和β的函數(shù),因此可令
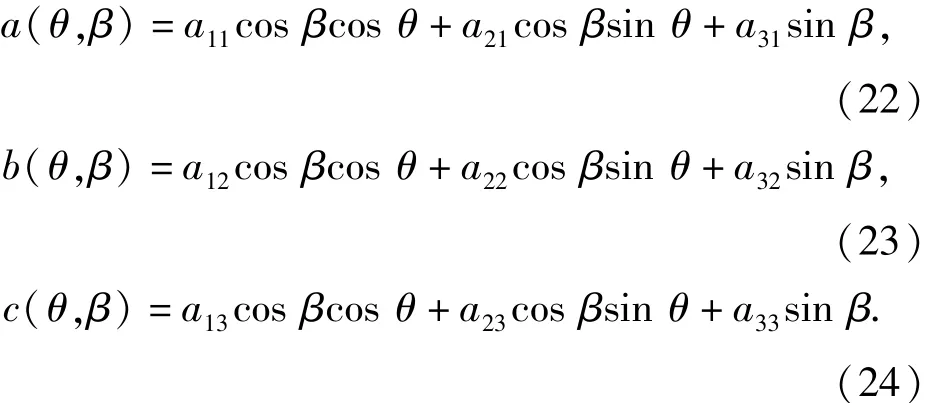
假設(shè)原始信號是由3個相互獨立的信號s1(t)、s2(t)和s3(t)組成,其中:s1(t)的循環(huán)平穩(wěn)頻率為α;s2(t)的循環(huán)平穩(wěn)頻率為ε;s3(t)為平穩(wěn)信號,即循環(huán)平穩(wěn)頻率為0.
由此,s'1(t)可以表示為
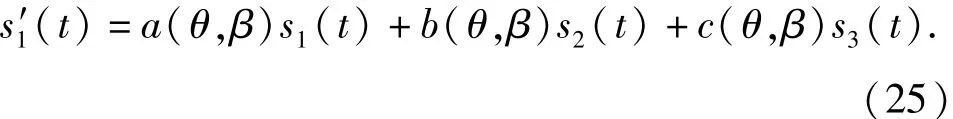
為了推導(dǎo)方便,將(25)式簡單記為
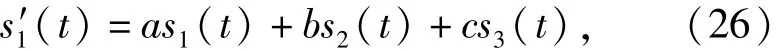
可以得到s'1(t)的循環(huán)平穩(wěn)累積量為
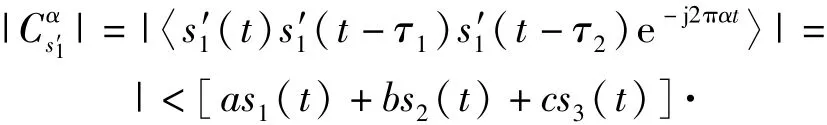
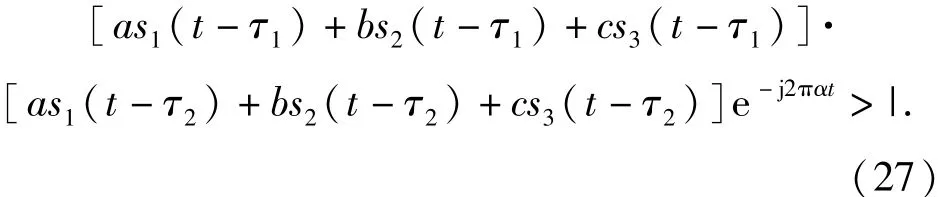
為了推導(dǎo)清晰,將si(t -τ1)與si(t -τ2)簡記為si(τ1)與si(τ2),將結(jié)果轉(zhuǎn)換成3階累積量形式,可得

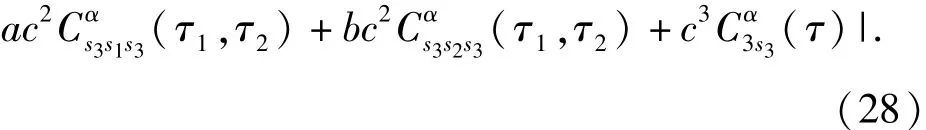
由于3路信號相互獨立,且s2(t)與s3(t)的循環(huán)平穩(wěn)頻率均不為α,由循環(huán)平穩(wěn)的性質(zhì)[17]可得
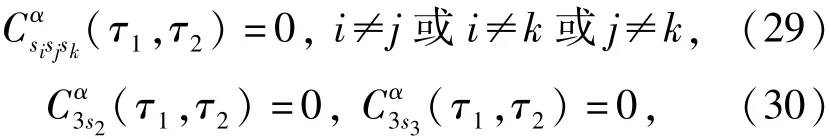
因此,s'1(t)的3階循環(huán)平穩(wěn)累積量為
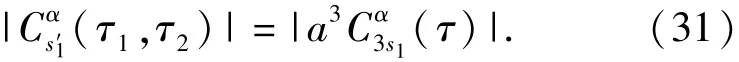
同理,計算零循環(huán)平穩(wěn)頻率處信號的3階循環(huán)平穩(wěn)累積為
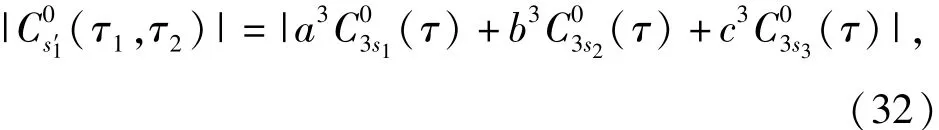
代入(15)式可得
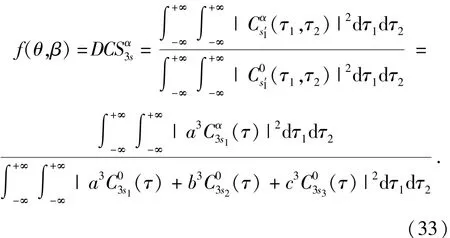
由于f(θ,β)是關(guān)于θ與β的函數(shù),其余部分可以看作常量,因此可令
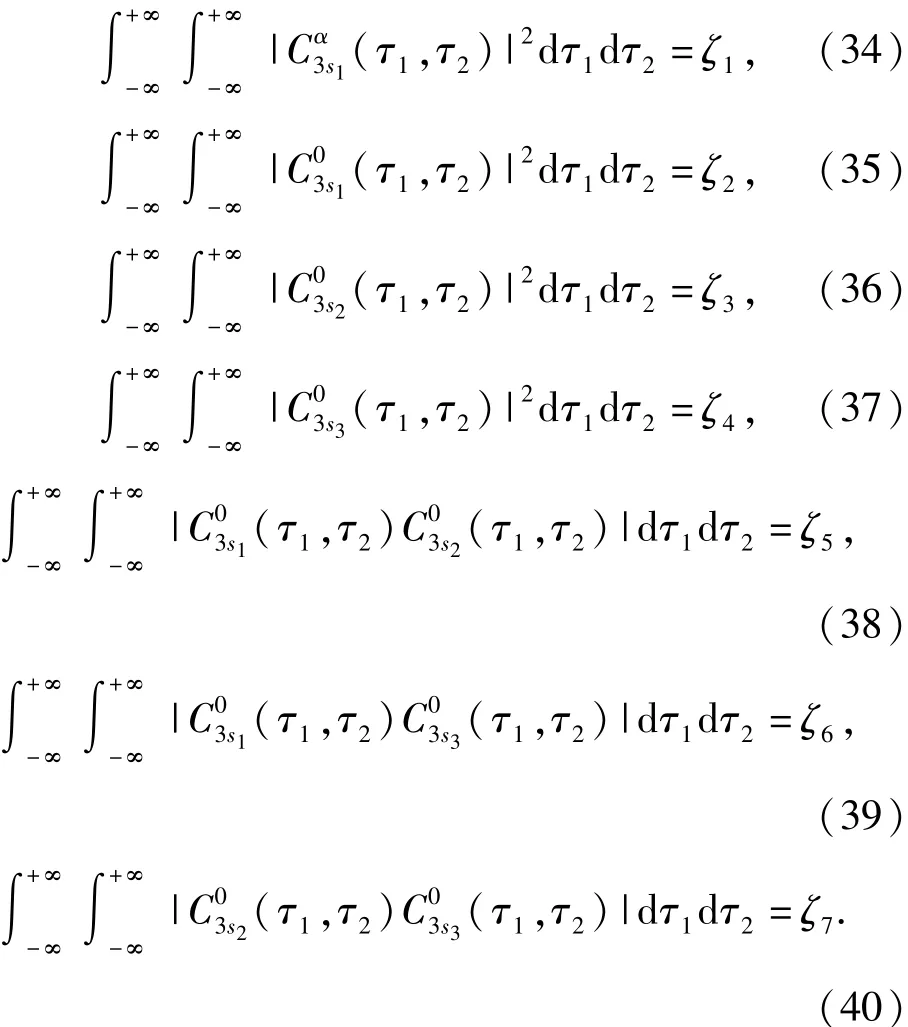
利用循環(huán)平穩(wěn)的性質(zhì)[17],可以將f(θ,β)簡化為
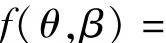
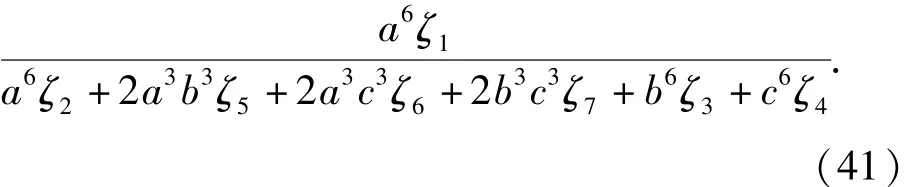
當a≠0時,(41)式可以化簡為
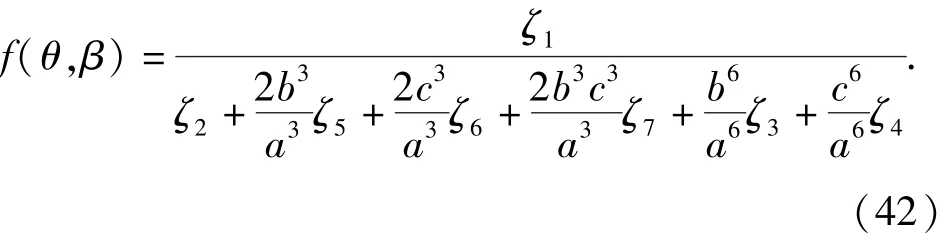
由于f(θ,β)是關(guān)于θ與β的函數(shù),對于θ求偏導(dǎo)數(shù)可得
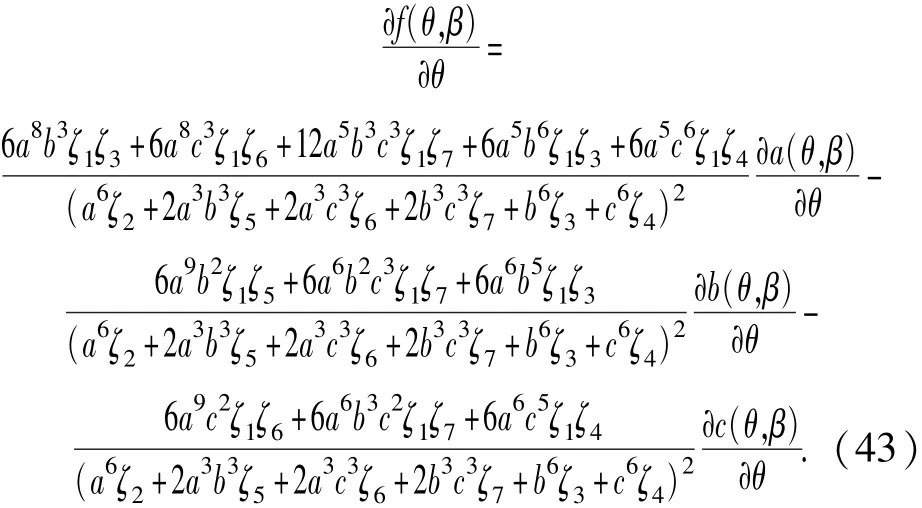
通過(42)式可以定性看出,b、c越小,目標函數(shù)越大。若b = c =0,目標函數(shù)將會取得最大值。
為進一步論證,將b = c = 0,a不為0,代入(43)式,可得

f(θ,β)關(guān)于θ的偏導(dǎo)數(shù)為0.同理,計算f(θ,β)關(guān)于β的偏導(dǎo)數(shù),并將b = c =0,且a不為0代入可得

此時θ、β為最佳旋轉(zhuǎn)角,因此通過求取最大的θ與β,即可用于構(gòu)造分離矩陣,且此時的G為最大值。
由上述的推導(dǎo)結(jié)果可得,當G取得最大值時,b 和c必然均為0,二者互為充要條件。計算出此時的θ與β,構(gòu)建分離矩陣,并由(25)式可得,當b = c =0時,得到的分離信號中沒有其他信號的成分,即通過求取目標函數(shù)的最大值實現(xiàn)了對多路混疊信號的分離。
通過上述數(shù)學(xué)推導(dǎo)證明,本文提出的Gives變換構(gòu)造分離矩陣的方法具有可行性。本算法拓展了原算法的適用范圍,將原來只能處理兩路信號,即有循環(huán)平穩(wěn)頻率的信號與不具備循環(huán)平穩(wěn)或循環(huán)平穩(wěn)頻率為0的信號,拓展到可以分離具有不同循環(huán)平穩(wěn)頻率的多路信號。從求解流程可以看出,本算法可以只基于一路偵收到的信號,通過構(gòu)建不同循環(huán)平穩(wěn)頻率下的目標函數(shù),對混疊信號逐次分離,實現(xiàn)欠定條件下的盲源分離。
4 仿真驗證
針對上述的推導(dǎo)與算法,進行仿真驗證。為體現(xiàn)本文算法的優(yōu)勢所在,在構(gòu)建仿真條件時,選取時域與頻域均出現(xiàn)混疊的信號。由于本文的算法對信號樣式?jīng)]有特殊要求,僅保證各信號的循環(huán)平穩(wěn)頻率不同即可。采用3路典型的信號,分別為線性調(diào)頻(LFM)信號s1(t)、調(diào)相信號s2(t)和環(huán)境噪聲高斯白噪聲s3(t),依次為
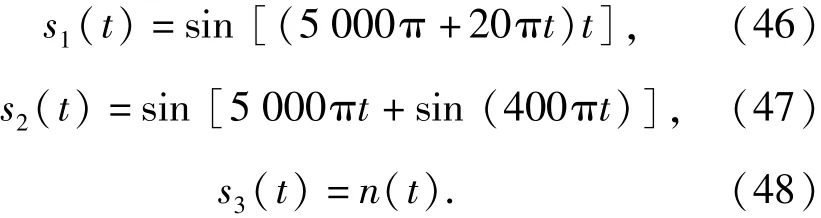
由(46)式~(48)式可知,LFM信號s1(t)的LFM斜率為2π,調(diào)相信號s2(t)的相位調(diào)制函數(shù)為sin(200πt),高斯白噪聲s3(t)服從均值為0、方差為1的標準高斯分布。取信號的時間長度為0. 1 s,三者同時到達,采樣時間為0. 000 1 s,且三者頻域出現(xiàn)混疊。圖2~圖4為上述3路信號的自相關(guān)函數(shù)圖。
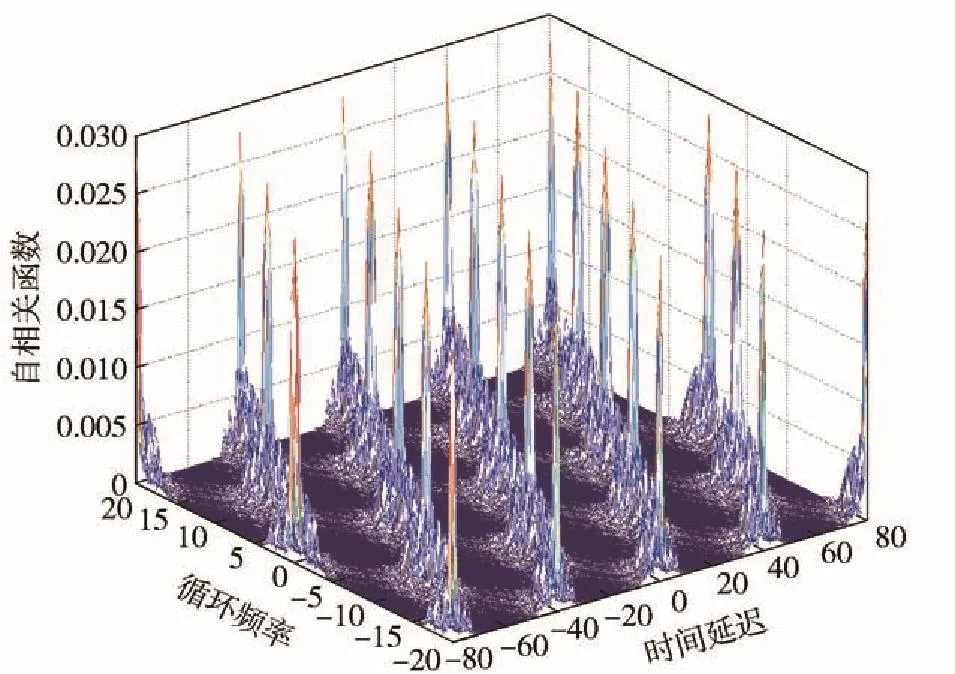
圖2 LFM信號的自相關(guān)與時延-循環(huán)頻率圖Fig. 2 The autocorrelation of LFM signal,time delay and cyclic frequency
由圖2、圖3可以直觀得到,信號的相關(guān)函數(shù)隨著時間差的改變而呈現(xiàn)周期性變化,由此可以得到LFM信號與調(diào)相信號具備循環(huán)平穩(wěn)特性,且周期性有所不同。由圖4可以得到,高斯白噪聲信號的自相關(guān)函數(shù)與時間差無關(guān),并沒有呈現(xiàn)周期性變化趨勢。進一步對自相關(guān)函數(shù)進行傅里葉變換,得到其譜相關(guān)密度函數(shù),如圖5~圖7所示。
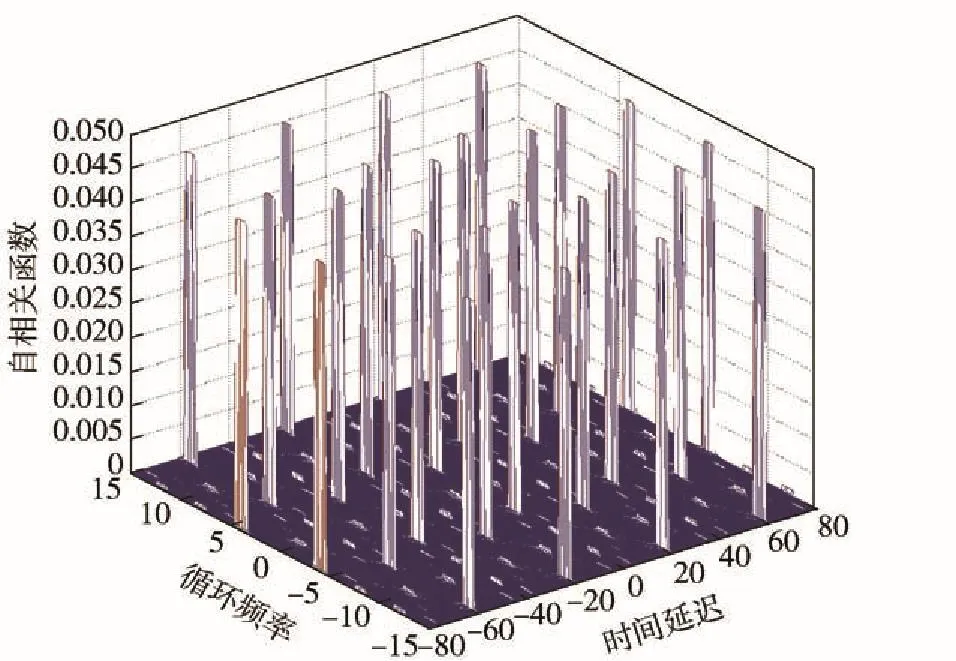
圖3 調(diào)相信號的自相關(guān)與時延-循環(huán)頻率圖Fig. 3 The autocorrelation of phase-modulated signal,time delay and cyclic frequency
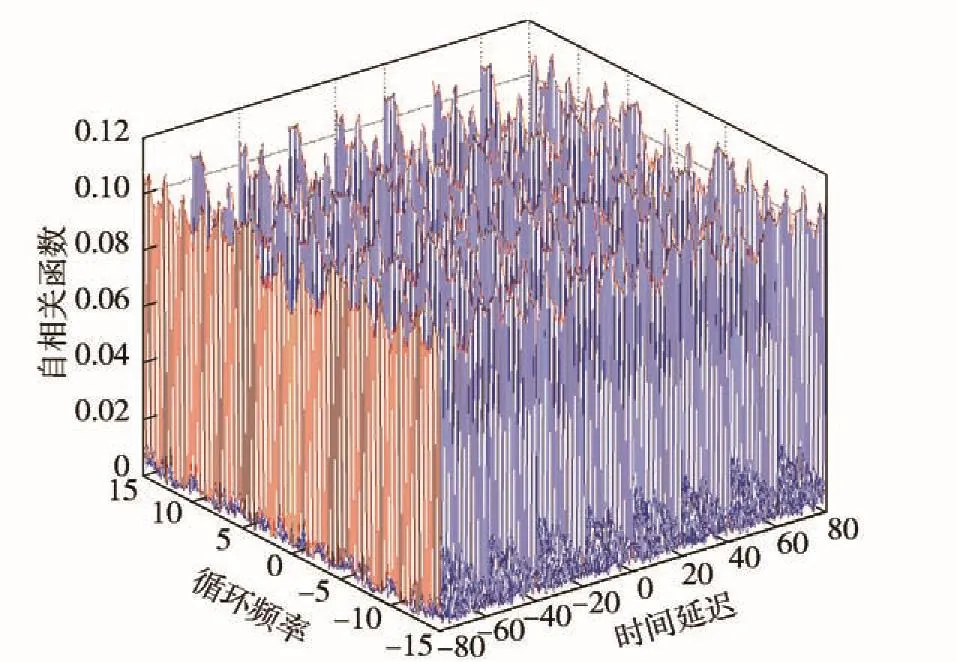
圖4 高斯白噪聲的自相關(guān)與時延-循環(huán)頻率圖Fig. 4 The autocorrelation of Gaussian white signal,time delay and cyclic frequency
從圖5、圖6可以清晰地看出,LFM信號與調(diào)相信號具備明顯的循環(huán)平穩(wěn)頻率,非零循環(huán)頻率不同且比較穩(wěn)定。從圖7中可以得出,高斯白噪聲信號在零頻處的信號功率譜密度函數(shù)值明顯高于其他頻點的數(shù)值。理論上,高斯白噪聲在非零處的循環(huán)平穩(wěn)頻率點應(yīng)為0.但由于仿真無法生成無限長的信號,隨機生成的高斯白噪聲只能體現(xiàn)部分的統(tǒng)計特征,因此在非零區(qū)域呈現(xiàn)出循環(huán)平穩(wěn)頻率。圖7中循環(huán)平穩(wěn)頻率主要集中在零頻處并高于其他點頻處,仿真比較接近真實情況。對比圖5~圖7可以看出,上述3種信號具備不同的循環(huán)平穩(wěn)頻率,且LFM信號與調(diào)相信號具有不同的非零循環(huán)頻率點,可以采用本文的拓展算法實現(xiàn)對信號的提取。
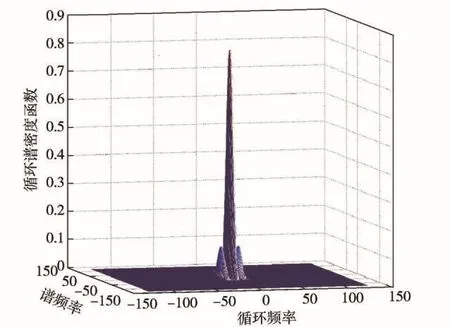
圖5 LFM信號的譜相關(guān)密度函數(shù)Fig. 5 CSD of LFM signal
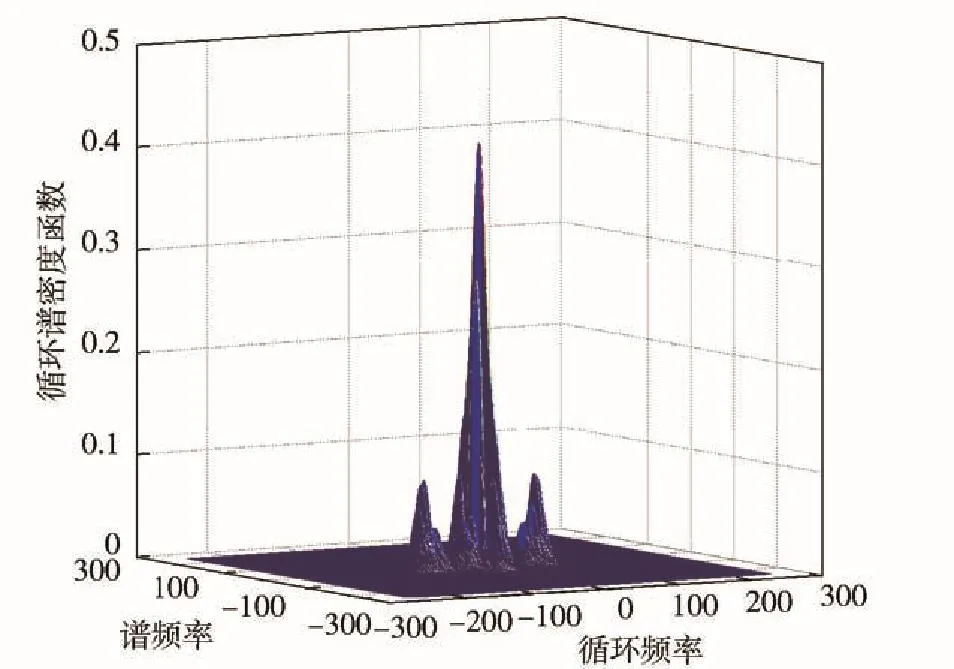
圖6 調(diào)相信號的譜相關(guān)密度函數(shù)Fig. 6 CSD of phase-modulated signal
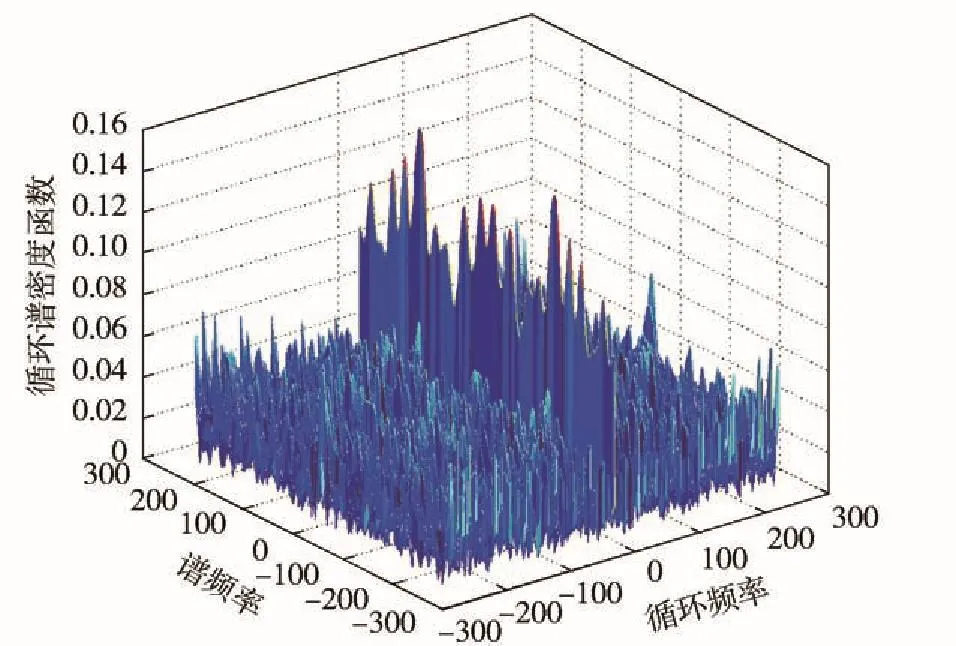
圖7 高斯白噪聲信號的譜相關(guān)密度函數(shù)Fig. 7 CSD of Gaussian white signal
采用本文擴展的DCS準則進行信號的分離與識別,混合矩陣為3×3的隨機高斯矩陣,并取其絕對值,得到的結(jié)果如圖8所示。
各路信號自身的特征較為明顯。當3路信號經(jīng)過隨機高斯矩陣的處理混疊在一起時,每個信號特征便被淹沒在混疊信號中。
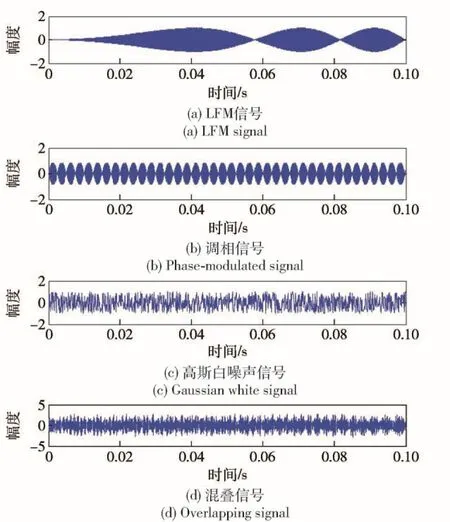
圖8 3種源信號與混疊信號Fig. 8 3 source signals and overlapping signal
進一步得到混疊信號的譜相關(guān)密度函數(shù),如圖9所示。

圖9 混合信號的譜相關(guān)密度函數(shù)Fig. 9 CSD of mixed signal
從圖9可以看出,3種信號在頻率維度上已經(jīng)出現(xiàn)混疊,無法直觀地鑒別出這3種信號。而在循環(huán)頻率維度上,雖然零頻處3種信號已經(jīng)出現(xiàn)混疊,且LFM信號強度較大,已明顯壓制住調(diào)相信號,但混疊信號的譜相關(guān)密度函數(shù)除去零點外還有明顯的強度峰值,進而可以采用本文拓展的算法,利用(15)式構(gòu)造函數(shù),使其強度峰值最大,得到旋轉(zhuǎn)角,用以構(gòu)建分離矩陣,實現(xiàn)對混疊信號的分離。
利用本文所拓展的算法對上述的混疊信號進行分離,得到結(jié)果見圖10.
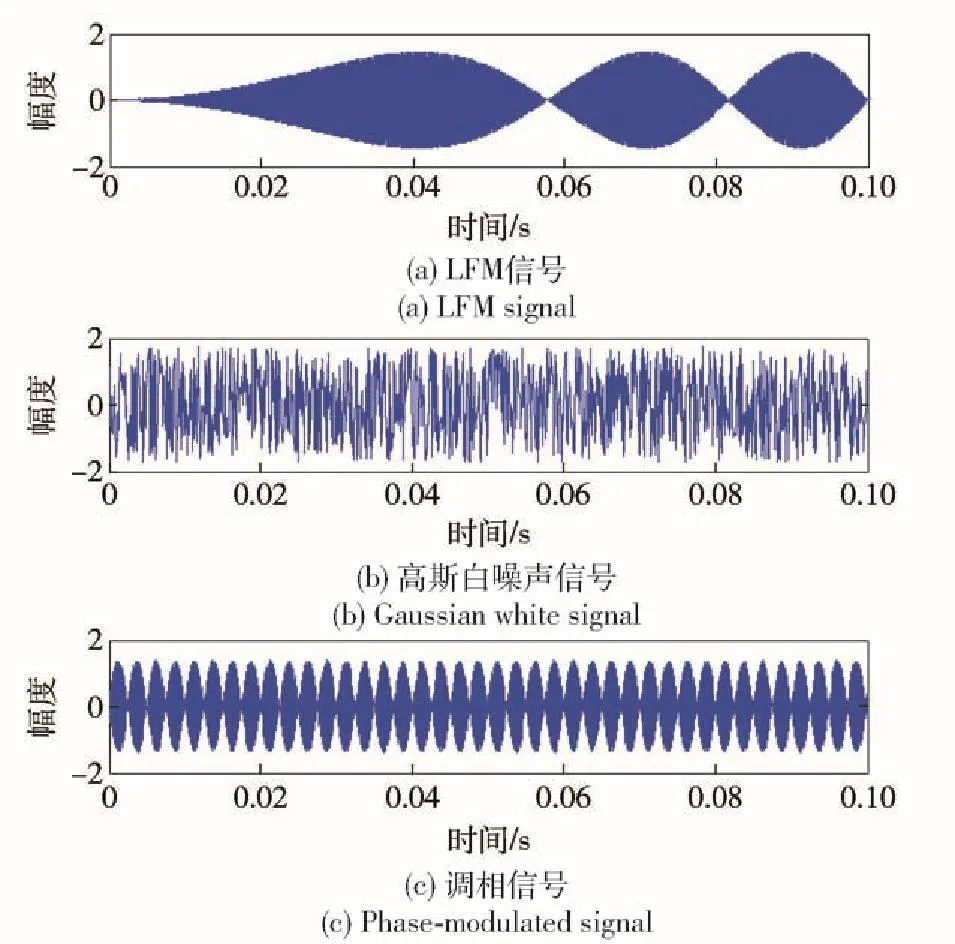
圖10 基于DCS準則的分離結(jié)果Fig. 10 The separating results based on DCS
從圖10中可以直觀看出,基于本算法對雷達信號分離與識別具有良好的效果,對比圖8中的原始信號相似度較大。本文采用分離信號與源信號的相似系數(shù)ξij作為衡量分離效果的性能指標,其定義式[20]為
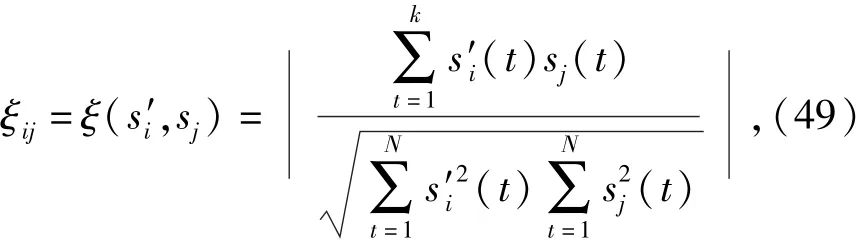
得到相似系數(shù)矩陣為

當相似系數(shù)的值高于0. 99時,可認為信號實現(xiàn)了良好的分離。由相似系數(shù)矩陣可以看出,LFM信號與調(diào)相信號的分離度較高。對高斯白噪聲的分離性能雖然較低,但分離出的信號實際應(yīng)用價值較低,因此可以不予考慮。通過仿真驗證實現(xiàn)了對多路雷達信號的分離,為后續(xù)提取信號的特征奠定了基礎(chǔ)。
2階循環(huán)累積量在計算信號的功率譜和自相關(guān)函數(shù)時只能用于零均值平穩(wěn)高斯過程的確認,對于非高斯過程則無法得到理想結(jié)果;時變高階累積量卻無法抑制非高斯噪聲。然而,本文提出的算法應(yīng)用范圍較廣且適用條件較為寬松,理論上要求源信號的循環(huán)平穩(wěn)頻率不同,即可實現(xiàn)盲源分離。通過上述的推導(dǎo)過程可以看出,本文拓展的算法可以實現(xiàn)欠定條件下的盲信號分離,其應(yīng)用范圍更寬泛。
5 結(jié)論
本文以現(xiàn)有的DCS準則下的盲信號分離理論為基礎(chǔ),通過構(gòu)造Givens矩陣將原始算法從只能分離二路信號向多路拓展,經(jīng)過公式推導(dǎo)論證了理論改進后的可行性,并給出了參數(shù)的確定方法與算法的適用條件。
由于不同雷達信號循環(huán)平穩(wěn)頻率有差異,本文從循環(huán)平穩(wěn)維度提取雷達信號在變換域的特征,實現(xiàn)對沒有先驗信息的雷達信號進行分離。
循環(huán)平穩(wěn)理論與基于高階累積量的盲源分離算法均可以保留系統(tǒng)的相位信息,對系統(tǒng)的辨識和參數(shù)估計極為有利,分離結(jié)果也很可觀。本算法運算量低,并能夠有效地抑制混合信號中的噪聲。本算法簡單,誤差小,實時性好,對于實際應(yīng)用有借鑒意義。
參考文獻(References)
[1] Latombe G,Granger E,Dilkes F A. Fast learning of grammar production probabilities in radar electronic support[J]. IEEE Transactions on Aerospace and Electronic Systems,2010,46(3):1262 -1289.
[2] Yang Z,Wu Z,Yin Z,et al. Hybrid radar emitter recognition based on rough k-means classifier and relevance vector machine. [J]. Sensors,2013,13(13):848 -864.
[3] Bezousek P,Schejbal V. Radar technology in the Czech Republic [J]. IEEE Aerospace and Electronic Systems Magazine,2004,19(8):27 -34.
[4] Yin Z,Yang W,Yang Z,et al. A study on radar emitter recognition based on SPDS neural network[J]. Information Technology Journal,2011,10(4):883 -888.
[5] Swiercz E. Automatic classification of LFM signals for radar emitter recognition using wavelet decomposition and LVQ classifier [J]. Acta Physica Polonica A,2011,119(4):488 -494.
[6] Ren M Q,Cai J Y,Zhu Y Q,et al. Radar emitter signal classification based on mutual information and fuzzy support vector machines[C]∥Proceedings of International Conference on Software Process. Beijing:IEEE,2008:1641 -1646.
[7] 關(guān)欣,孫迎豐,何友.不完備信息系統(tǒng)的輻射源識別方法研究[J].電子科技大學(xué)學(xué)報,2008,37(1):8 -11. GUAN Xin,SUN Ying-feng,HE You. Study on emitter recognition to incomplete information system[J]. Journal of University ofElectronic Science and Technology of China,2008,37(1):8 -11.(in Chinese)
[8] 張葛祥,金煒東,胡來招.基于粗集理論的雷達輻射源信號識別[J].西安交通大學(xué)學(xué)報,2005,39(8):872 -875. ZHANG Ge-xiang,JIN Wei-dong,HU Lai-zhao. Radar emitter signal recognition based on rough set theory[J]. Journal of Xi’an Jiaotong University,2005,39(8):872 -875.(in Chinese)
[9] 林云,司錫才,周若琳,等.改進灰色關(guān)聯(lián)算法在輻射源識別中的應(yīng)用[J].通信學(xué)報,2010,31(8A):166 -171. LIN Yun,SI Xi-cai,ZHOU Ruo-lin,et al. Application of improved grey correlation algorithm on radiation source recognition [J]. Journal on Communications,2010,31(8A):166 - 171.(in Chinese)
[10] He Z,Shen Y,Wang Q,et al. Mitigating end effects of EMD using non-equidistance grey model[J]. Journal of Systems Engineering and Electronics.2012,23(4):603 -611.
[11] 李楠,曲長文,蘇峰,等.雷達輻射源模糊識別算法改進[J].電子科技大學(xué)學(xué)報,2010,39(2):182 -185. LI Nan,QU Chang-wen,SU Feng,et al. Improved radar emitter fuzzy identification algorithm[J]. Journal of University of Electronic Science and Technology of China,2010,39(2):182 -185.(in Chinese)
[12] Wang J G. Emitter target recognition based on multi-sensor data fusion of ESM and IR[C]∥The 9th International Conference on Signal Processing Proceedings. Hefei:Electronic Engineering Institute,2008:1508 -1511.
[13] 周憲英,張懷巍,關(guān)欣.基于灰度量空間的輻射源識別方法[J].計算機與數(shù)字工程,2013,41(2):192 -195. ZHOU Xian-ying,ZHANG Huai-wei,GUAN Xin. A GMS-based emission source identification method[J]. Computer & Digital Engineering,2013,41(2):192 -195.(in Chinese)
[14] 黃知濤,周一宇,姜文利,等.循環(huán)平穩(wěn)信號的處理與應(yīng)用[M].北京:科學(xué)出版社,2006. HUANG Zhi-tao,ZHOU Yi-yu,JIANG Wen-li,et al. Processing and application of cyclostationary signal[M]. Beijing:Science Press,2006.(in Chinese)
[15] 湯輝,王殊.基于去噪盲分離的多個直擴信號參數(shù)估計[J].系統(tǒng)工程與電子技術(shù),2011,33(8):1722 -1726. TANG Hui,WANG Shu. Parameters estimation of DSSS based on denoising source separation[J]. Systems Engineering and Electronics,2011,33(8):1722 -1726.(in Chinese)
[16] 于寧宇,馬紅光,石榮,等.基于二階循環(huán)統(tǒng)計量的BPSK參數(shù)估計[J].系統(tǒng)工程與電子技術(shù),2011,33(9):2117 -2121. YU Ning-yu,MA Hong-guang,SHI Rong,et al. Parameter estimation of BPSK via second-order cyclic statistics[J]. Systems Engineering and Electronics,2011,33(9):2117 - 2121.(in Chinese)
[17] 李燈熬,趙菊敏.循環(huán)平穩(wěn)理論的盲源分離算法[M].北京:國防工業(yè)出版社,2015. LI Deng-ao,ZHAO Ju-min. Blind source separation principles and algorithms based on cyclostationary theory[M]. Beijing:National Defense Industry Press,2015.(in Chinese)
[18] Bi G,Chen J,He J,et al. Application of degree of cyclostationarity in rolling element bearing diagnosis[J]. Key Engineering Materials,2005,293/294:347 -354.
[19] Zhao J M,Li D A,Zhang H Y. Second order blind source separation algorithm[J]. Journal of Computational Systems,2011,7(3):979 -983.
[20] Liu H Y,Zhao J M,Li Deng A. Single guide league ventricular late potentials extraction based on signal correlation[J]. Journal of Information and Computational Science,2013,10(14):4673 -4680.
Multichannel Radar Signal Recognition Algorithm Based on DCS
WANG Hong-wei1,F(xiàn)AN Xiang-yu2,CHEN You2,YANG Yuan-zhi2
(1. School of Electronic and Information,Northwestern Polytechnical University,Xi’an 710072,Shaanxi,China;2. Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi’an 710038,Shaanxi,China)
Abstract:Recognizing the radar signal in complex electromagnetic environment is the necessary prerequisite for electronic countermeasures to play a role. The priori information about signal modulation and signal parameter is limited,which cannot provide enough intelligence support for signal sorting. In addition,the mixture of signals restricts the effectiveness of signal sorting. The issue mentioned above is converted to a blind source separation. A high-order disjunction matrix is established with Givens transform,and the blind source separation algorithm with degree of cyclostationarity(DCS)based on the third-order cyclic statistics which is suitable for two channel signals is expanded to the multichannel signals with different cyclostationarity frequencies. The feasibility of the proposed method is proved by theoretical derivation,and the method for establishing the parameters of Givens matrix is derived. The features of radar signal in cyclostationary domain are extracted with cyclostationarity theory. The method is simulated with DCS separation principles. The simulated results show that the algorithm can realize the effective sorting of multichannel radar signals.
Key words:radar engineering;signal recognition;cyclostationarity frequency;Givens matrix;DCS blind source separation algorithm;multichannel signal
中圖分類號:TN97
文獻標志碼:A
文章編號:1000-1093(2016)04-0661-09
DOI:10. 3969/ j. issn. 1000-1093. 2016. 04. 013
收稿日期:2015-07-16
基金項目:航空科學(xué)基金項目(20145596025、20152096019)
作者簡介:王紅衛(wèi)(1974—),男,副教授,碩士生導(dǎo)師。E-mial:hww0818@163. com;

