卡方分布的性質與應用探討
杜 蒙
(榆林市第一中學,陜西 榆林 719000)
一、卡方分布的理論概述
若n個相互獨立的隨機變量均服從標準正態分布,則這n個均服從標準正態分布的隨機變量的平方和構成一個新的隨機變量,其分布規律稱為卡方分布。其中參數n稱為自由度,自由度不同卡方分布就不同。從以上的定義介紹中我們可以看出,卡方分布實際上是由正態分布構造而成的一個新的分布,這也正說明了正態分布在數理統計中的重要作用。卡方分布是概率論和統計學中重要的一種開率分布。卡方分布常用于假設檢驗和置信區間的計算。
二、卡方分布的性質
1.卡方分布的圖像分布在第一象限,且呈正偏態.
2.卡方分布隨著自由度增加而逐漸趨向于對稱,df很大時接近正態分布,當df趨向于正無窮大時,分布即為正態分布。
3.卡方分布只有一個參數,即自由度n,不同的自由度決定不同的卡方分布,自由度越小,分布越偏斜。
4.卡方分布的均值為自由度n,記作Eχ2=n,這里的符號“E”是表示對隨機變量取平均值的意思;卡方分布的方差為二倍的自由度,即為Dχ2=2n,這里的符號“D”表示對隨機變量求方差。
5.卡方分布具有可加性:如果k個服從卡方分布而且相互獨立的隨機變量,則它們的和仍然服從卡方分布,這個新的卡方分布的自由度為原來的k個卡方分布自由度之和。
6.不管自由度n是多少,卡方分布曲線下的面積都是1.
7.卡方值都是正數。
三、卡方檢驗的應用
1.卡方檢驗的簡單介紹
卡方檢驗的基本步驟是:第一步,建立原假設H0(正常情況下結論,不以否定的)和備擇假設;第二步,根據理論分布或者理論經驗建立期望頻數;第三部,由實際頻數和計算出來的期望頻數來計算樣本的卡方值,卡方檢驗的基本公式是:
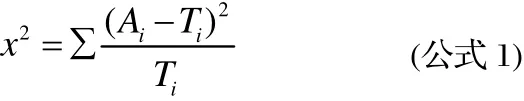
其中,表示實際頻數,表示期望頻數,表示卡方值。在實際應用中,調查資料或者實驗得出的若干個實際頻數與理論頻數之間的差別可以用公式一來表示,如果樣本量足夠大,要是大于40而且理論頻數大于5,則公式一就近似服從卡方分布,樣本來那個越大,近似程度就越好;第四步,根據顯著性水平α和自由度在卡方分布概率表中找出相對應的卡方臨界值,如果卡方臨界值小于運算得出的卡方值,就接受原假設,如果卡方臨界值大于運算得出的卡方值,就拒絕原假設,接受備擇假設。在卡方分布的應用研究中,常用于兩種情況:擬合度檢驗和獨立性檢驗,下面我們就論證了這兩種應用。
2.單一因素的卡方擬合度檢驗
我們都知道,影響一個事物的因素可能是多種多樣的。同樣的,在非參數檢驗過程中,只有一個因素改變的檢驗成為單因素檢驗,多個因素同時改變的檢驗成為多因素檢驗。擬合度檢驗是對已經制作好的預測模型進行檢驗,比較它們的預測結果與實際發生情況之間的吻合度。
2.1 檢驗數據之間有無差異性
檢驗觀測的數據之間的差異性是比較簡單的單因素卡方檢驗,只是簡單的檢驗了分成多項的頻數之間在數量上有無明顯的差異。下面這個例子是這一檢驗在語言研究中的應用。
例為了了解學生學習數學的動機,我們做了一次小范圍的問卷調查,這次問卷分為了5個項目,調查了100名普通高校大一學生,調查問卷的結果如表二所示。現在的問題是,從問卷調查結果分析學生學習數學的動機有無顯著性差異?

表一學生學習英語的動機實際頻數表
上表所給的數據是計數數據而且樣本量不大,比較適合用卡方擬合度檢驗。問題具體分析步驟如下:
(1)建立原始假設和備擇假設。原始假設認為每個學生學習數學的動機之間沒有明顯的差異;備擇假設則認為學生學習英語的動機有明顯的差異。
(2)計算出期望頻數。如果學生學習數學的動機沒有明顯的差異,則100名學生對5個項目的選擇概率應該是相等的,所以期望頻數的公式是:期望頻數=總數/分類的項目數
將表一中的數據代入公式2,得出的結果是:期望頻數=總數/分類的項目數=100/5=20
(3)計算卡方值。
(4)計算自由度。在這個問題中共有5個分類項目,即比較5個分類項目的頻數,但是在實際計算中,最后一個分類項的頻數是由全部頻數減去前面4個頻數所得到的,因此實際上只有4個獨立信息。所以計算這類檢驗的自由度公式是:df=n-1=5-1=4,所以自由度是4.
(5)查表。查表可知,當自由度為4時,顯著性水平位0.05,卡方臨界值是 9.49。
(6)得出結論。由于計算出的卡方值23.9大于12.6,這說明觀測數據之間存在著明顯的差異,因此拒絕原假設接受備擇假設,也就是說學生學習數學的動機是存在著明顯差異的。
2.2 檢驗樣本分布與理論分布模型之間的擬合度
單因素卡方檢驗中的另一個重要的用途是檢驗樣本分布與特定分布模型或者某一理論分布模型是否擬合,下面這個例子是檢驗樣本是否服從孟德爾遺傳定律。
例按照孟德爾的遺傳定律,讓開淡紅色花的豌豆隨機交配,子代可以開出紅花、淡紅花、白花三類,它們的比例是1:2:1,為了驗證這個理論,我們特別安排論了一個實驗,實驗得到的開紅花、淡紅花、白花的豌豆的株數分別是26,,66,28,現在的問題是驗證這些數據與孟德爾遺傳定律是否一致。
如果以分別表示隨機交配的豌豆開紅花、淡紅花、白花這一事件,那么孟德爾遺傳定律認為,
p1=,為了驗證這些數據與孟德爾遺傳定律是否一致,就是要檢驗
現在共進行了n=26+66+28=120次觀測,其中發生的頻數分別是26,66,28,而在原始假設下期望的頻數是30,60,30,所以

查閱卡方分布概率表得,在自由度為2,顯著性水平為0.05時,卡方分布的臨界值是5.991,大于1.267,因此不能拒絕原始假設,即實際數據與孟德爾的理論模型沒有顯著差異。
3.多因素卡方檢驗
卡方檢驗除了能進行擬合度檢驗之外,還能進行分析倆個或多個因素之間有無關聯。下面我們來介紹卡方檢驗在列聯表獨立性檢驗和四個表獨立性檢驗中的應用研究。
3.1 列聯表獨立性檢驗
隨機試驗的結果往往要記錄各個研究對象的兩個或者多個分類屬性。這時樣本中具有各個屬性的頻數統計就需要按照各個屬性的交叉分類進行。特別的,在兩個分類屬性時,往往要用一個矩形表來列出兩個屬性交叉分類下每種組合的頻數,這種表就稱作為列聯表。有一種2×2的列聯表叫做四格表。
3.2 齊一性的卡方檢驗
匯總在兩向列聯表中的數據,在采集的時候可有各種不同的情況。有時候其中兩個屬性不能都看為是隨機的。
例如在流行病的研究中,為了研究得病與否與某個生活習慣的關系,往往預先規定對一定數量的患者與非患者進行觀測。例如,在下表中就是對262名心血管病人和519名(大體上兩倍)無心血管疾病的公民詢問他們是否有吸煙史的調查結果。希望由此來比較在這兩個人群中有吸煙史的比例是不是相同。

?
在上表所示的數據中,被調查的心血管病患者與非心血管病患者的比列是262::519。這個采樣比例是根據研究的需要確定的,但是這個比列并不能反映出整個人群中患病的人與不患病的人的比例。因此在分析這個數據的時候,不應該將患病與否這個屬性作為隨機的。而是應該講這兩個人群分別作為不同的總體,在這兩個總體中比較其吸煙者的比列。
四、結束語
綜上所述,我們主要研究的是卡方分布的八條性質和卡方分布在現實生活中的應用。本文的難點就是在研究列聯表獨立性檢驗和齊一性卡方檢驗時,卡方統計量的推導以及列聯表獨立性檢驗和齊一性卡方檢驗的區別,也就是說不是很明確在什么情況下用列聯表獨立性檢驗,什么時候用齊一性檢驗,雖然最后的卡方統計量的計算公式是一樣的,但是其中的原理確實有很大差異的。

