粒子群算法及其在船舶結構中的優化應用

郭　雷,郭幼丹,余思騫,黃曉恒

(1.集美大學 a.輪機工程學院；b.機械與能源工程學院，福建 廈門 361021；2.中船黃埔文沖船舶有限公司，廣州 510715)

粒子群算法及其在船舶結構中的優化應用

郭雷1a,郭幼丹1b,余思騫1b,黃曉恒2

(1.集美大學 a.輪機工程學院；b.機械與能源工程學院，福建 廈門 361021；2.中船黃埔文沖船舶有限公司，廣州 510715)

摘要：以基于慣性權值改進的離散型粒子群算法為優化方法，使用中部單個艙段重量作為算法的適應度值，選用直接計算法計算各工況下所得板的中面應力和梁的軸向應力均需小于許用應力作為約束條件，對某按規范設計的12 000 DWT油船中部艙段進行優化。結果表明，該方法使船中部艙段鋼料使用量相對初始設計下降了9.26%，實現了減輕船體結構的目標。

關鍵詞：粒子群算法；直接計算法；結構優化；船體艙段

船舶結構的“輕量化”一直是船舶設計的重要問題。同型的船舶較小的船體鋼材用量可能使船舶擁有更大的載重量。我國所設計同等船型船舶大多數空船重量都較日韓歐美等國偏重，這在一定程度上說明我們在船舶輕量化方面明顯存在不足。本文選用一種具有群體智能的粒子群算法[1-2]，并結合船體結構強度的直接計算法對某12 000 DWT油船進行中部艙段結構的優化。

1粒子群算法

1.1算法原理

PSO(particle swarm optimization，PSO)算法將種群中的個體被視為沒有體積和質量的粒子。假設有m個粒子組成的種群，在面臨d維問題時(即目標的搜索空間是d維的)，每個粒子(粒子所處的位置即該問題的一個可能解)在空間中以一定的速度飛行，如粒子i(i=1,2,…,m)在第t次迭代時所在的位置和飛行速度表示為Xi(t)=(Xi1(t),Xi2(t),…,Xid(t))和Vi(t)=(Vi1(t),Vi2(t),…,Vid(t))。則在第t次飛行結束后，粒子i會根據自身以及群體中其他粒子的飛行經驗對自身的飛行位置Xi(t)和速度Vi(t)作出動態調整，速度和位置的更新公式為：

(1)

式中：k為迭代次數；w為慣性權重；c1、c2均是學習因子，但分別與粒子自身歷史最優pik(t)和種群歷史最優pgk(t)有關，即向“自身”或“社會”學習的程度。每個粒子在尋優過程中會根據自身歷史最優值pik(t)和種群的最優值pgk(t)來調整自身速度和位置，最優值由適應度函數來判斷。

1.2算法流程

標準PSO算法流程[3-4]如下：①隨機初始化粒子的位置和速度；②計算每個粒子的適應值；③對每個粒子，將其適應值與個體極值進行比較，如果較優，則更新當前的個體極值，與全局極值進行比較，如果較優，則更新當前的全局極值；④根據式(1)、(2)更新每個粒子的位置和速度；⑤如未達到預先設定的停止準則(通常為最大迭代次數kmax)，則返回步驟②，若達到則停止計算。

2PSO在船舶結構優化中的應用

2.1設計變量

在優化過程中，選取板材的板厚和骨材截面尺寸為設計變量。涉及優化的構件，縱向上為各板材的板厚以及各縱向骨材尺寸；橫向構件主要是肋板、橫艙壁以及橫向強框架。本船初始設計縱骨主要為球扁鋼，保持型材類型不變，通過自建球扁鋼的型材庫，按照截面面積按自然數順序1、2、3,…進行編號。設計變量的取值范圍：板厚以其初始設計厚度為中心，步長為1 mm，每種骨材以其初始編號為中心，步長為1，2者均左右取5步作為取值范圍。最終共有板材設計變量18個，骨材設計變量共5個。

各設計變量所在位置及其編號見圖1，所有設計變量可表示為X=(X1,X2,X3,…,X23)。

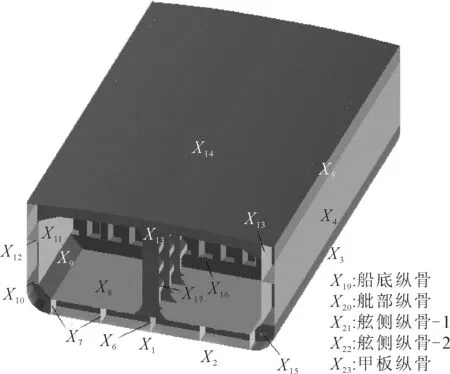
圖1　各設計變量位置及編號

2.2適應度函數

適應度函數為該船中部單個艙段的重量，艙段的質量可表示為

(3)

式中：ρi、Vi為各變量Xi所對應密度和體積。

2.3約束條件

約束條件按規范選取為板的中面應力和梁的軸向應力均需小于許用應力(見表1)，共得12個約束條件，即

(4)

式中：j=1,2,3,…,12。

表1　各結構部位及其強度衡準比[5-6]

2.4優化流程

優化流程見圖2。

圖2　PSO算法在船舶結構中的優化流程

PSO算法優化船舶結構的過程實際上是對各設計變量的組合變換。初始時，算法在各結構的可選位置范圍內隨機產生一群結構組合方案(方案的數量由粒子種群數目決定)，然后結合直接計算法校核，并計算各組合方案的艙段重量，隨后求出組合方案中個體極值和全局極值。根據式(1)、式(2)更新各結構組合方案中然后通過更改各結構組合中下次迭代的尺寸規格、規格更新步長，迭代尋優直到滿足終止條件或達到最大次數位置，輸出最優結構尺寸組合。

3船體直接計算法模型

3.1本船主尺度及結構型式

本船載重量約為12 000 t，全船采用橫向和縱向混合骨架形式，貨油艙區域的上甲板、雙層底、雙殼處采用縱骨架式。總長Loa=134.85 m，型寬B=22.00 m，型深D=10.60 m，設計吃水d=7.50 m，結構吃水ds=7.80 m。按文獻[7]規定，建立1/2+1+1/2貨艙艙段模型。

3.2網格劃分

有限元網格沿橫向和垂向以縱骨間距為一個單元，縱向以肋距為一個單元，橫向為縱骨間距。網格形狀主要為正方形，有極少量三角形單元。在ANSYS中使用的單元類型主要為Shell63和Beam188，網格劃分見圖3。

圖3　艙段模型的網格劃分

3.3計算載荷及邊界條件

計算載荷主要包括：①艙室內貨物壓力；②外部靜水和波浪水動壓力；③端面彎矩。其中①、②按照規范根據實際裝載情況計算，本文為了保證優化結構具有足夠的強度在③中端面彎矩施加選擇該載況下船中處的最大值，其中靜水彎矩Ms按裝載手冊由COMPASS軟件計算(各載況實際數值見圖4)，波浪彎矩Mw按下式計算。

圖4　典型工況下的船體彎矩值

3.4ANSYS中實現的技術要點

優化過程中適應度函數的評價要求在ANSYS軟件中進行，因此需注意以下技術要點。

1) 有限元計算過程是自動進行的。

2) 設計變量的離散化和迭代過程中的更新。

3) 反復自動的建立幾何模型、網格劃分、各工況的載荷加載以及結果后處理中龐大的計算量(以kmax為100，種群數量為10，4種工況為例，就需進行10×100×4=4 000次有限元計算)。

3.5處理方法

1) 直接計算法的各步驟操作全部使用參數化設計語言(ANSYS parametric design language, APDL)完成，并保存成批文件形式；

2) 使用離散型PSO算法，在初始化或者迭代過程中，結構組合方案中板材的厚度和骨材的規格編號(自建型材庫中為連續的自然正整數)均通過MATLAB建立數組并以txt文件保存的文件供ANSYS讀取作為實常數或截面型號。

3) 在建立幾何模型后保存成DB格式的數據文件，迭代計算時在批文件中利用APDL調用DB文件，省去反復建模的步驟[8]；而網格劃分、各工況載荷的處理、結構的后處理通過建立的宏命令自動加載進行；在網格劃分后，對于質量大出初始設計過多的結方案不予繼續有限元計算。

4參數設置及優化結果

本文使用基于慣性權值改進的離散型PSO算法進行優化，其中改進慣性權重w使用線性遞減的方法，該方法在初期w值較大，保證了算法的全局搜索能力；后期w值較小，保證了算法的區域搜索能力[2]，具體計算按式(6)進行。

(6)

式中：w1和w2分別為w的初始值和最終值；CurIter和MaxIter分別為算法的當前代數和最大迭代代數。學習因子c1=c2=2.05，最大迭代次數kmax設置為足夠大，所得結構的最優尺寸組合結果見表2。

結果表明，中部單個艙段重量的優化結果相對于初始設計下降了9.26%。以簡單的對比優化前后壓載狀況下的有限元計算結果發現，優化后的船體von Mises應力有所提高(見圖5)，但提高的幅度并不太大。

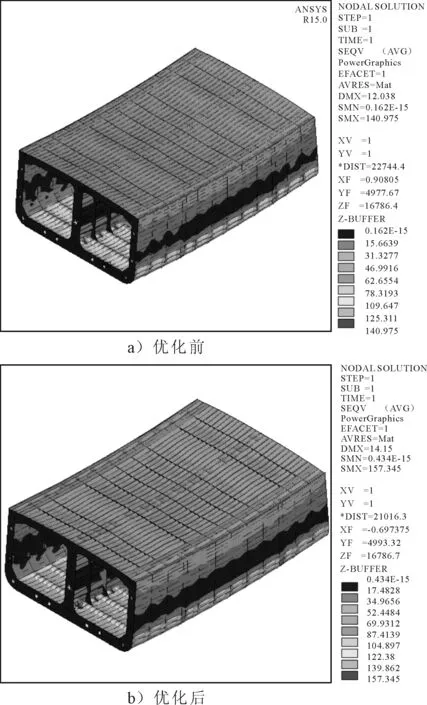
圖5　優化前后von Mises應力對比(壓載出港)

mm

5結論

采用粒子群算法對船舶結構進行優化，優化結果良好。而且使用有限元方法和PSO算法相結合，可以考慮到各工況下結構強度的實際需要。但仍有諸多問題需要解決。

1) 約束條件僅考慮到屈服強度是不夠的，未能需將屈服強度和節點疲勞、規范要求的最小尺寸等一些更加符合實際應用的約束計入。

2) PSO算法與其他智能算法一樣，也是一種概率型算法，有經常陷入局部最優情況的發生。如何設置參數使其更適合與船體結構的優化，還需進一步實驗測試。

3) 本文僅考慮4種典型工況，未來需考慮船舶的營運中其他工況，以及到全船結構的優化。

參考文獻

[1] 江岳文,陳沖,溫步瀛.含風電場的電力系統機組組合問題隨機模擬粒子群算法[J].電工技術學報,2009(6):129-137.

[2] 王翠翠,朱大奇,劉靜.基于粒子群優化卡爾曼濾波的水下機器人信號處理[J].船海工程,2010(1):99-102.

[3] KENNEDY J, EBERHART R C. Swarm intelligence[M]. USA: Academic Press,2001.

[4] 紀震,廖慧連,吳青華.粒子群算法及應用[M].北京：科學出版社,2010.

[5] 楊永謙,肖金生.實用有限元分析技術:ANSYS專題與技巧[M].北京：機械工業出版社,2010

[6] 熊志鑫.船體結構有限元建模與分析[M].上海：上海交通大學出版社,2014.

[7] 中國船級社.油船結構強度直接計算指南2003[M].北京:人民交通出版社,2003.

[8] 林少芬,朱兆一.船體分段吊裝吊碼布置綜合優化研究[J].船舶工程,2014(2):77-80.

Particle Swarm Optimization and Its Application to Ship Structural Optimum

GUO Lei1a, GUO You-dan1b, YU Si-qian1a, HUANG Xiao-heng2

(1a. College of Marine Engineering; 1b. College of Mechanical and Energy Engineering, Jimei University, Xiamen Fujian 361021, China;2. CSSC Huangpu-Wenchong Shipbuilding Co. Ltd., Guangzhou 510715, China)

Abstract:An improved discrete particle swarm optimization (DPSO) is investigated to optimize a 12 000 DWT tanker structure. In the optimization process, the weight of a cabin in midship is chosen as fitness function with the constraint condition of that the stress calculated by direct strength analysis should be less than allowable stress. The optimization results show that last optimum design reduces by 9.26 percent of steel consumption.

Key words:particle swarm optimization; direct strength analysis; structural optimum; block of hull

DOI:10.3963/j.issn.1671-7953.2016.03.014

收稿日期：2015-12-17

基金項目：福建省自然科學基金項目(2014J01200)；福建省科技計劃引導性項目(2016H0023)

第一作者簡介：郭雷(1990—)，男，碩士生 E-mail:jmuguolei@163.com

中圖分類號：U661.4

文獻標志碼：A

文章編號：1671-7953(2016)03-0059-04

修回日期：2016-01-06

研究方向:船體結構設計