蘇里格氣田含水氣藏廢棄地層壓力確定的新方法

鄭臘年，安紅燕，達麗娜，霍明會

（1.中國石油長慶油田分公司蘇里格氣田研究中心氣藏動態研究，陜西西安　710018；2.低滲透油氣田勘探開發國家工程實驗室，陜西西安　710018；3.中國石油長慶油田分公司，陜西西安　710018）

?

蘇里格氣田含水氣藏廢棄地層壓力確定的新方法

鄭臘年1，2，安紅燕1，2，達麗娜3，霍明會1，2

（1.中國石油長慶油田分公司蘇里格氣田研究中心氣藏動態研究，陜西西安710018；
2.低滲透油氣田勘探開發國家工程實驗室，陜西西安710018；3.中國石油長慶油田分公司，陜西西安710018）

摘要：蘇里格氣田是典型的致密砂巖氣藏，儲層不但致密，非均質性強，氣井產量低，且多數產水，氣藏采收率低。廢棄地層壓力是氣藏采收率的關鍵影響因素之一，對于不產水氣藏可以通過單相二項式產能方程結合經濟極限產量綜合確定，但對于產水氣藏廢棄地層壓力的確定國內外研究不多。本文針對蘇里格氣田產水氣藏，以最小攜液速度下的產氣量與產水時經濟極限產氣量相結合共同確定了廢棄產量區間范圍，應用質量守恒原理推導得出氣水兩相產能公式，最終求取含水氣藏廢棄地層壓力的一種新方法，并對影響因素進行分析。本文利用VC編程采用多次迭代計算，提高了計算精度，為產水氣藏廢棄地層壓力的求取及采收率的確定提供了一種新思路。

關鍵詞：含水氣藏；二項式產能方程；廢棄產量；廢棄地層壓力

廢棄地層壓力是計算氣藏采收率或可采儲量的重要參數，也是有關地面工程論證和設計的重要指標和依據。對于不產水氣藏可以通過單相二項式產能方程結合經濟極限產量綜合確定［1-3］，但對于產水氣藏，目前有余貝貝、唐海等［4］提出的以氣井最小攜液速度為約束條件，通過復合半徑模型確定地層產水時氣井的穩定二項式產能方程進行求取，但它存在的問題是復合半徑參數求取的不確定性，以及復合半徑模型不能得出不同水氣比下的傷害程度，給這種方法的應用帶來一定的局限性。

本文根據質量守恒原理推導出來的產水氣井二項式產能方程，以多種集輸條件下的氣井最小攜液流量和產水時經濟極限產量為約束，最終獲得了產水氣井廢棄地層壓力，并對影響廢棄地層壓力因素進行分析。

1　含水氣藏廢棄地層壓力確定方法

1.1廢棄井口壓力

自噴開采井廢棄井口壓力等于最低外輸氣壓力，蘇里格上古井流程外輸壓力為3MPa，下古井流程外輸壓力為6.4MPa。隨著氣田深入開發，在一級增壓以及多級增壓的情況下，氣井的最小集輸井口壓力可低至0.5MPa。

1.2廢棄井口產量

對于產水氣井，隨著地層壓力的下降，氣井最大產氣量不斷降低，當最大產氣量低于最小攜液速度下的產氣量時，此時氣井將不能正常生產，對應產氣量即為廢棄井口產量。

目前，比較常見的臨界攜液流量模型主要有Turner模型、李閩模型和王毅忠模型。對于蘇里格氣田，王毅忠模型與實際生產情況比較接近，故本文采用王毅忠模型來計算廢棄井口壓力下對應的臨界攜液流量即廢棄井口產量：

其中：

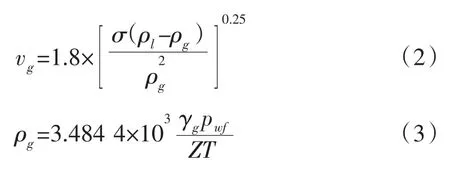
式中：qSC-最小攜液產氣量，m3/d；pwf-井底流動壓力，MPa；vg-氣體流速；A=πd2/4-油管內截面積，m2；d-油管內徑，m；T-氣流溫度，K；Z-天然氣偏差系數；σ-界面張力，對水取60 mN/m；ρl-液體密度，kg/m3，水取1 074 kg/m3；ρg-天然氣密度，kg/m3；γg-天然氣相對密度。

1.3廢棄井底流壓

已知廢棄井口壓力和井口產量，代入到井底流壓計算公式中，便可算出廢棄井底流壓，其公式如下：

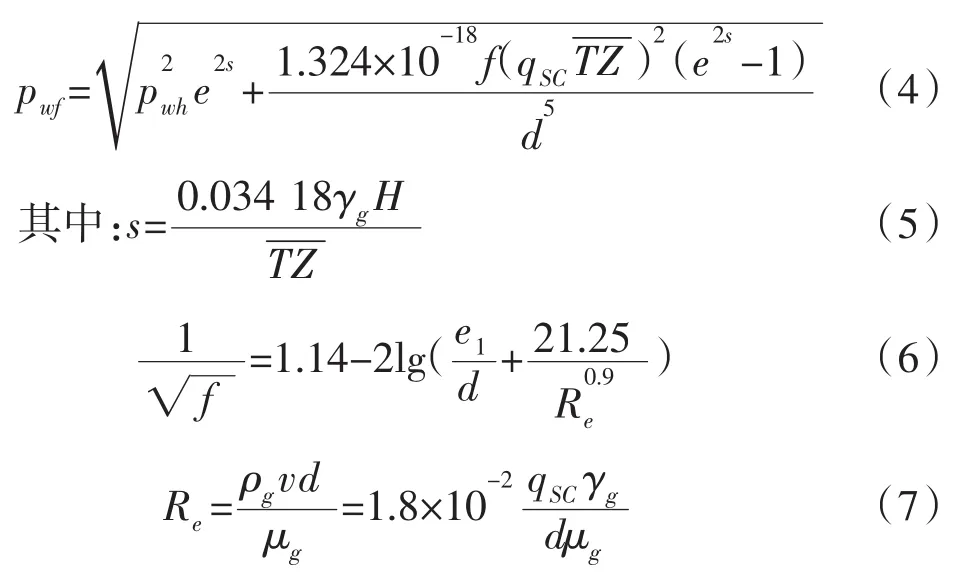
式中：pwh－井口油壓，MPa；H－氣層中深，m；e1－管壁粗糙度，m；μg－一定溫度壓力下的天然氣黏度，mPa·s。

由于垂直段隨著井深的變化井筒的壓力和溫度都會發生變化，從而引起了偏差系數和黏度的變化，為了計算更加準確，本文將垂直井段以每米為單位劃分單元，每個單元計算出相應的平均偏差系數和黏度進行迭代計算。步驟如下：

（1）劃分單元，確定基本參數。

（2）假設下一單元的初始壓力，讓它等于上一單元的壓力。取它們的平均值求出本段相應的壓力。

（3）根據平均壓力和平均溫度計算出擬壓力和擬溫度，進而計算出下一段的偏差系數和黏度等參數。

（4）采用式（4）求出下一段壓力。

（5）用計算出來的壓力跟假設的壓力值作比較，若兩者比較接近時，則計算出來的壓力即為所求，否則將計算出的壓力作為迭代值，重復步驟（2）～（4）繼續計算直到滿足精度為止。

（6）重復上面的步驟，直到計算到井底。

根據上述步驟，利用VC編制相應程序，從而得出氣井垂直井筒壓力分布曲線（見圖1），從圖1中可以看出井筒壓力隨井深呈線性增加。

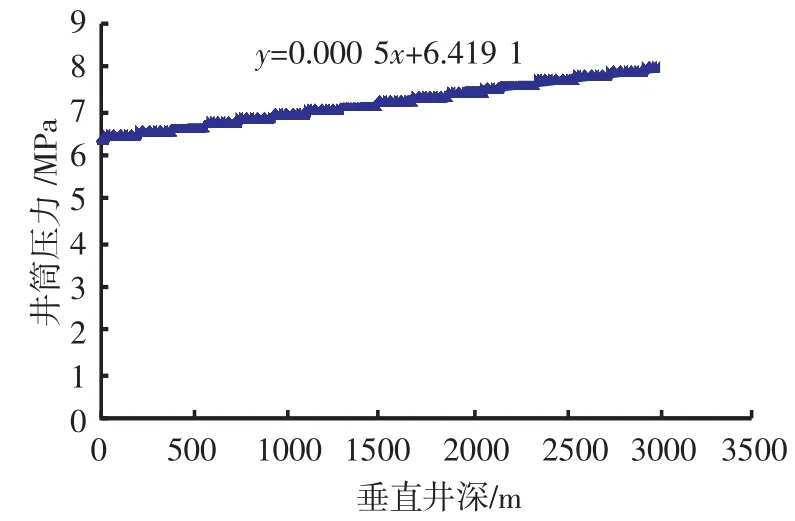
圖1　井筒壓力隨井深變化的關系曲線

1.4廢棄地層壓力確定方法

1.4.1產水氣井產能方程的確定對于產水氣井，引入氣水兩相擬壓力函數。

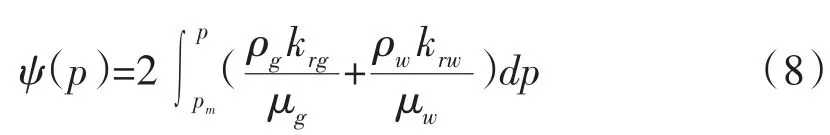
同時考慮表皮系數和高速非達西滲流的影響，推導出產水氣井二項式產能方程，如下式所示：

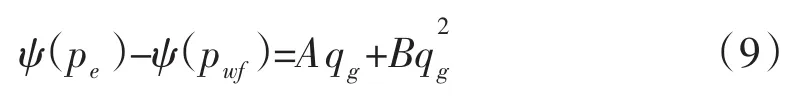
其中：

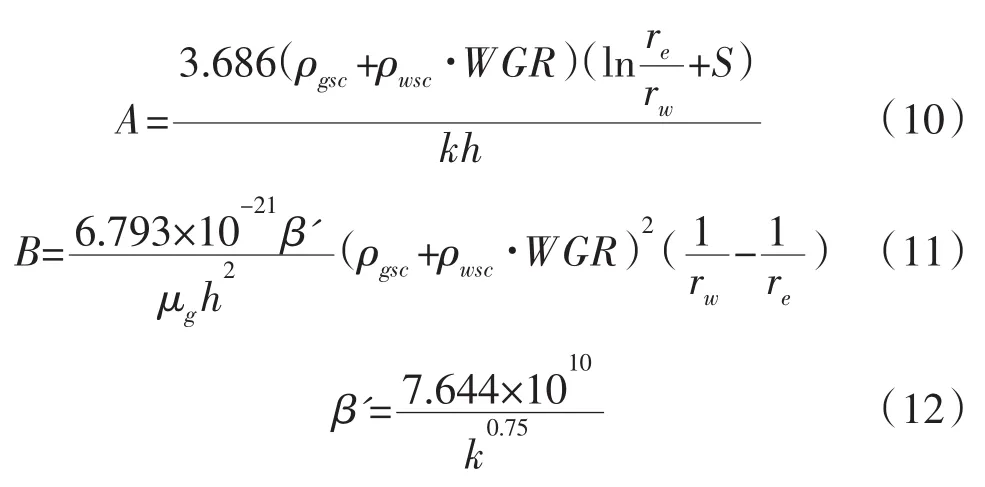
式中：ψ（p）-擬壓力，kg·MPa/（m3·mPa·s）；krg-氣相相對滲透率；krw-水相相對滲透率；μw-一定溫度壓力下的水相黏度，mPa·s；ρgsc-地面標準狀況下氣體密度，kg/m3；ρwsc-地面標準狀況下水密度，kg/m3；WGR-水氣體積流量之比，m3/m3；re-供給半徑，m；rw-井口半徑，m；S-表皮系數；k-儲層滲透率，10-3μm2；h-氣層有效厚度，m。

該產能方程中引入兩相擬壓力公式比用壓力平方計算精度高，此外引入水氣比這個參數，進而可以計算不同水氣比對廢棄地層壓力影響。

1.4.2兩相擬壓力與地層壓力的關系根據儲層巖心氣水相對滲透率曲線，可以得出兩相擬壓力與地層壓力的關系曲線（見圖2），從圖2中可以看出，隨著壓力的增大，氣水兩相擬壓力隨之增大。

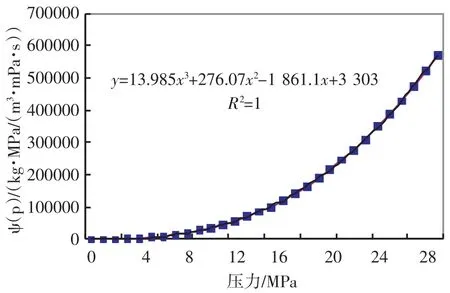
圖2　兩相擬壓力與壓力的關系曲線

1.4.3二項式產能系數與地層壓力的關系從式（10）、（11）中可以看出，在氣井開采過程中假設表皮系數S不變，當地層壓力下降時，二項式系數A值不變，式（11）中的黏度將會發生變化從而影響B值的變化。假設氣井在不同開采階段的二項式產能系數分別為B1和B2且對應的天然氣黏度分別為μg1和μg2，那么根據式（11）有：

根據上式作出二項式系數B隨地層壓力變化的關系曲線（見圖3）。

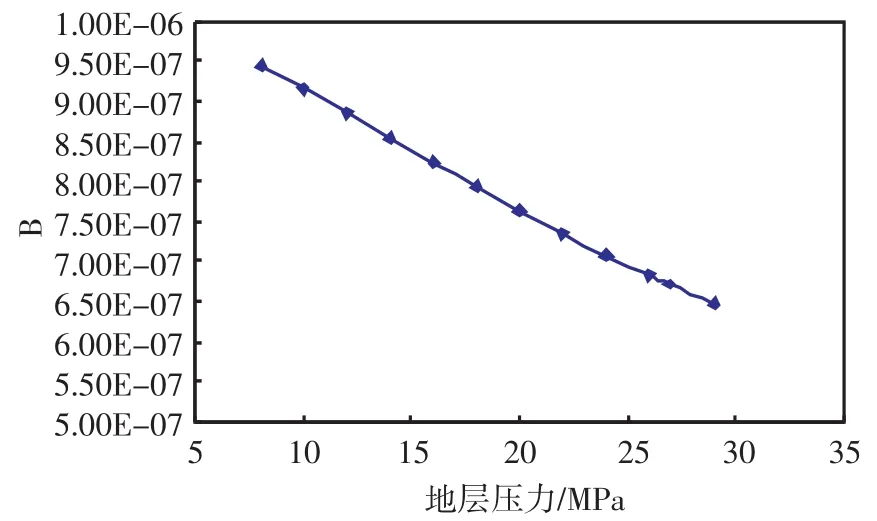
圖3　B值隨地層壓力變化曲線

由圖3知，B值隨地層壓力的降低逐漸增加，因此若始終采用初期建立的穩定產能方程來計算廢棄地層壓力必將帶來誤差。

1.4.4廢棄地層壓力計算由1.2和1.3節確定出廢棄產量和廢棄井底流壓后，代入到二項式產能公式（9）中，從而可以求出對應的廢棄地層壓力。但是具體計算中存在的難點是：在求解二項式系數B時需要先得到廢棄條件下的天然氣黏度，而求解又需要知道廢棄地層壓力，然而氣井的廢棄地層壓力本身就是需要求解的參數，是未知的，因此需要采用迭代計算方法。利用VC編制程序，求解廢棄地層壓力，其具體步驟為：

（1）令廢棄地層壓力p的初始迭代值p0為原始地層壓力；

（3）按式（9）計算ψ（p），根據ψ（p）與p的關系，求出對應的p值；

（4）若計算出來的值p與假定的值p0相差很小，則計算出來的壓力即為所求的廢棄地層壓力；否則，取p0=p，重復（2）～（3）步，直到滿足要求。

2　實例應用

本文以SX區塊為例，該區塊滲透率介于0.06 mD～2.457 mD，平均值為0.510 mD。有效厚度介于2m～22.7m，平均值為8.6m，氣層平均中部埋藏深度3 556m，原始地層壓力31MPa，水氣比平均為0.8m3/104m3。

考慮多種集輸條件下的情況，計算出對應的臨界攜液流量，進而求出廢棄井底流壓，再利用產水氣井二項式產能公式，得到產水氣藏廢棄地層壓力，同時計算出產水經濟極限產量下對應的廢棄地層壓力，其結果（見表1）。

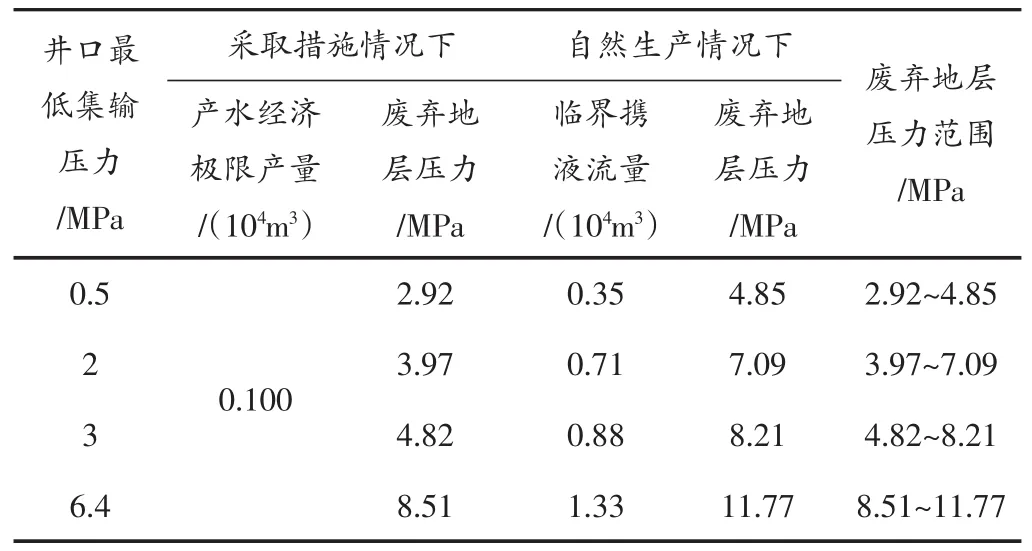
表1　不同集輸條件下廢棄地層壓力情況

從表1中可以看出，不同集輸條件下，廢棄地層壓力差異比較大。在自然生產條件下，其臨界攜液流量即為其極限產量，計算出來的廢棄地層壓力要大于采取措施下的廢棄地層壓力，因此對于產水氣藏廢棄地層壓力最小值為采取措施情況下計算的廢棄地層壓力值，最大值是自然生產遞減到臨界攜液流量時對應的廢棄地層壓力，此壓力范圍對產水氣藏的開發具有實際指導意義。

此外，考慮產水井需采取排水采氣措施，其經營成本有所增加，計算出產水和不產水情況下對應的廢棄地層壓力，其結果（見表2）。

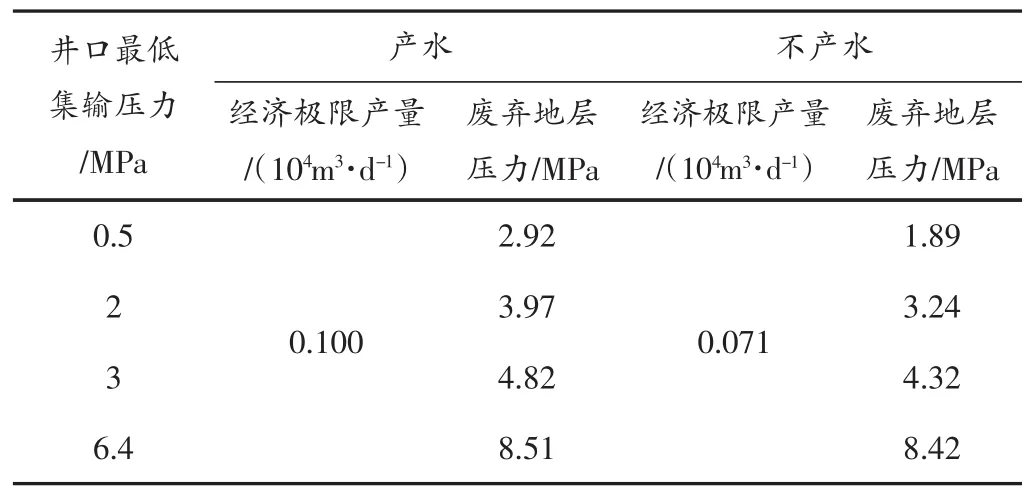
表2　產水和不產水情況下廢棄地層壓力對比表

從表2中可以看出，水的存在會使廢棄地層壓力增加，同時井口集輸壓力越小，水的影響越大，廢棄地層壓力增加的幅度也越大。因此對于產水氣井廢棄地層壓力的計算需要采用產水氣井二項式產能方程，不能用單相產能公式代替。

3　廢棄地層壓力影響因素分析

根據上述理論公式，結合SX區塊各項基本參數，分別作出氣層滲透率、有效厚度、井口最低集輸壓力、水氣比對廢棄地層壓力的影響曲線（見圖4～圖7）。

3.1滲透率的影響

從圖4可以看出，在滲透率較低時，廢棄地層壓力隨滲透率的增加明顯減小，而在滲透率較高時，廢棄地層壓力隨滲透率的增加變化很小，有一明顯分界點，即在滲透率高于0.2 mD后廢棄地層壓力趨于平緩。說明在低滲條件下，廢棄地層壓力對滲透率非常敏感，而在滲透率較高時則影響很小。

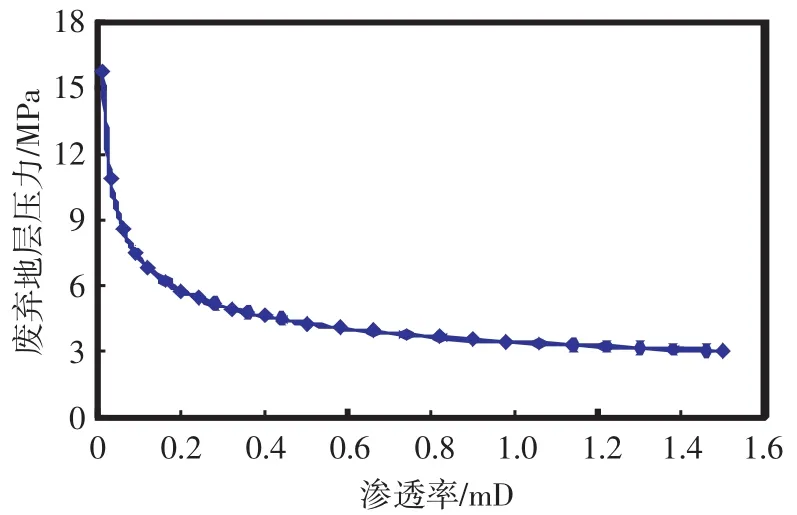
圖4　滲透率對廢棄地層壓力的影響

3.2氣層有效厚度的影響

考慮不同地層滲透率條件下有效厚度變化對廢棄地層壓力的影響，從圖5中可以看出，隨著有效厚度的增加，廢棄地層壓力逐漸降低。此外，當儲層滲透率較低時，隨有效厚度的增加，廢棄地層壓力降低幅度比較大；而在滲透率較高時，廢棄地層壓力降低的幅度較小。說明儲層滲透率較低時，廢棄地層壓力對有效厚度比儲層滲透率高時更敏感。

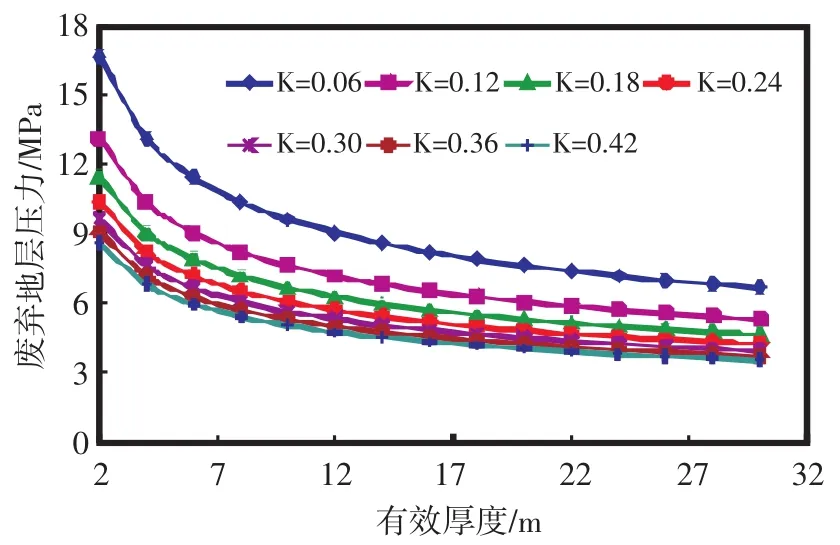
圖5　有效厚度對廢棄地層壓力的影響

3.3井口最低集輸壓力的影響

不同井口最低集輸壓力下廢棄地層壓力隨有效厚度變化的關系曲線，從圖6中可以看出，廢棄地層壓力隨井口最低集輸壓力的增加而增大。

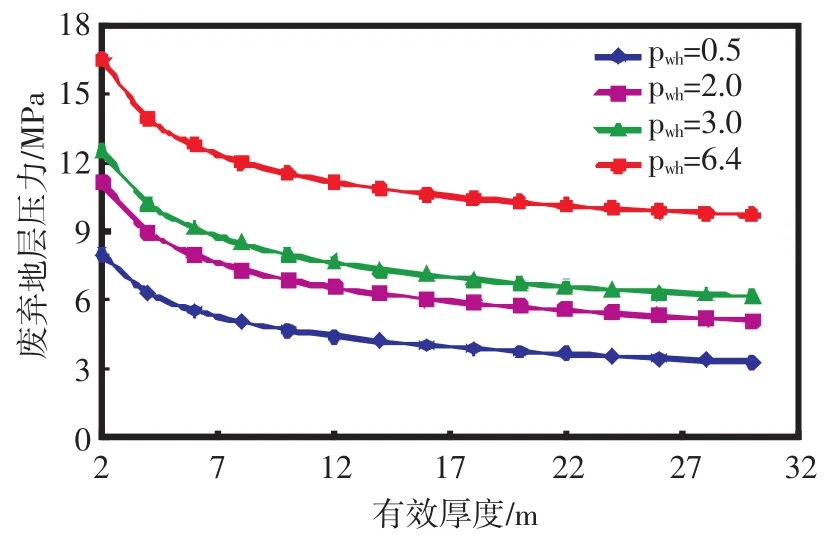
圖6　井口最低集輸壓力對廢棄地層壓力的影響

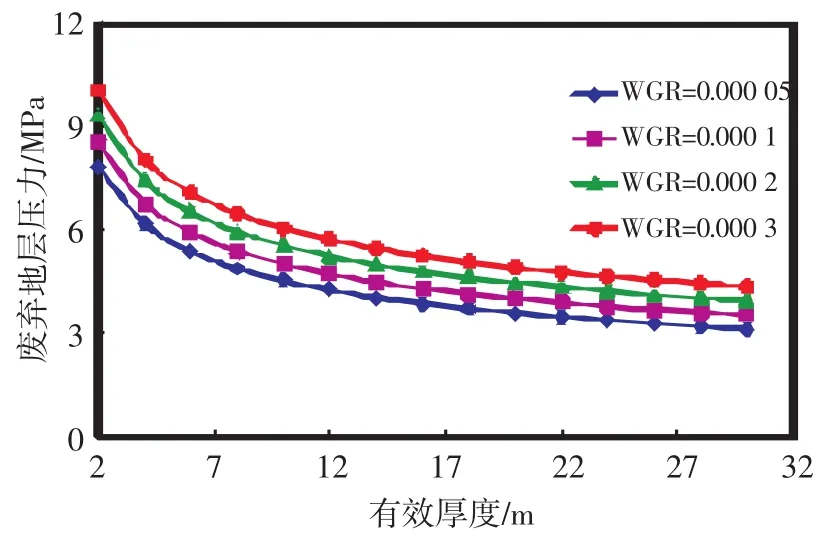
圖7　水氣比對廢棄地層壓力的影響

3.4水氣比的影響

不同水氣比條件下廢棄地層壓力隨有效厚度變化的關系曲線，從圖7中可以看出，廢棄地層壓力隨水氣比的增加而增大。由此可知，水的存在對廢棄地層壓力的影響不容忽視。

4　結論

（1）針對產水區塊，在自然生產情況下，提出了以臨界攜液流量為極限產量，利用產水氣井二項式產能方程評價廢棄地層壓力。該方法計算的結果大于采取措施情況下的廢棄地層壓力，為廢棄地層壓力的上限值，對產水氣藏的開發有實際指導意義。

（2）隨著氣井地層壓力的下降，二項式系數A值不變，B值不斷增加，因此必需用廢棄時的產能方程計算廢棄地層壓力。

（3）廢棄地層壓力隨儲層滲透率的增加逐漸降低，當滲透率小于0.2 mD，滲透率對廢棄地層壓力的影響十分明顯；當滲透率大于0.2 mD，滲透率對廢棄地層壓力的影響不明顯。

（4）廢棄地層壓力隨有效厚度的增加而減小，且儲層滲透率較低時，廢棄地層壓力對有效厚度比儲層滲透率高時更敏感。

（5）隨著井口最低集輸壓力和水氣比的增加，廢棄地層壓力逐漸增大，水的存在對廢棄地層壓力的影響不容忽視。

參考文獻：

［1］郝玉鴻，閻紀輝.確定氣井廢棄地層壓力的新方法［J］．油氣采收率技術，1999，6（4）：77-82．

［2］鄒建波，李閩，代平，等．氣藏廢棄壓力和采收率影響因素［J］.新疆石油地質，2006，27（6）：736-739．

［3］盧濤，蘭義飛，何磊．一種計算氣藏廢棄壓力的方法-二項式產能方程法［J］．天然氣勘探與開發，2009，32（2）：18-20．

［4］余貝貝，唐海，李東林，等．產水氣藏廢棄壓力的確定方法［J］．新疆石油地質，2008，29（5）：641-643.

A new model of determination of abandonment pressure in water bearing gas reservoir in Sulige gasfield

ZHENG Lanian1，2，AN Hongyan1，2，DA Lina3，HUO Minghui1，2
（1.Sulige Gasfield Research Center of PetroChina Changqing Oilfield Company，Xi'an Shanxi 710018，China；2.National Engineering Laboratory for Exploration & Development of Low-Permeability Oil & Gasfield，Xi'an Shanxi 710018，China 3.PetroChina Changqing Oilfield Company，Xi'an Shanxi 710018，China）

Abstract:Sulige gasfield is typical of tight sandstone gas reservoirs. The reservoir not only compact，strong heterogeneity，low gas production，and high water production. The gas reservoir recovery has many factors. Abandonment formation pressure is one of the key factors that influence gas reservoir recovery. For no water gas reservoir can be integrated to determine by single-phase binomial productivity equation combined economic output limit，but for producing water gas reservoir，research of abandonment formation pressure is not much. For Sulige gasfield，this paper proposed a new method for calculating abandonment formation pressure，which used gas water two phase productivity formula derived from principle of mass conservation and combine with abandonment gas production rate range by determined by gas production at the minimum liquid carring rate and economic limit production of waterproduction. To improve accuracy，we use VC programming using multiple iterative calculations. This paper provides a new idea for caculating water gas reservoir abandonment formation pressure and recovery.

Key words：water bearing gas reservoir；binomial deliverability equation；abandonment production rate；abandonment formation pressure

中圖分類號：TE377

文獻標識碼：A

文章編號：1673-5285（2016）06-0075-05

DOI:10.3969/j.issn.1673-5285.2016.06.019

*收稿日期：2016－05-16

作者簡介：鄭臘年（1986-），2013年畢業于西南石油大學油氣田開發工程專業，現在長慶油田蘇里格氣田研究中心工作，從事氣藏工程方面的研究工作，郵箱：zln.0404@163.com。