“探索規律”教學的規律探索

【關鍵詞】推理能力；規律；探索規律；和與積的奇偶性

【中圖分類號】G623.5 【文獻標志碼】A 【文章編號】1005-6009（2016）26-0058-03

【作者簡介】王海峰，江蘇省南通師范學校第二附屬小學（江蘇南通，226001）副校長，一級教師，南通市數學學科帶頭人，江蘇省小學數學基本功大賽一等獎獲得者。

《義務教育數學課程標準（2011年版）》指出：推理能力的發展應貫穿于整個數學學習過程中。推理是數學的基本思維方式，也是人們在學習和生活中經常使用的思維方式。發展小學生的推理能力是小學數學教學的重要任務之一。基于此，各個版本的小學數學教材除了系統編排常規的數學知識外，還精心安排了各種“探索規律”的教學內容，這些內容責無旁貸地成為發展學生推理能力的重要載體。“探索規律”的教學究竟應該關注什么？“探索規律”的教學是否也存在一定的規律？下面，筆者以蘇教版五下《和與積的奇偶性》一課為例，談談自己的教學實踐與思考。

“和與積的奇偶性”是教材基于“因數和倍數”單元的學習，精心安排的探索規律的教學內容，旨在讓學生通過舉例、觀察、比較和歸納，發現和與積的奇偶性規律，積累探索規律的經驗，發展推理能力。從英國科學哲學家邁克爾·波蘭尼的默會認識論的角度來看，對于和與積的奇偶性規律是什么，學生不難發現和歸納，也可以準確地描述和表達，屬于明確知識。而對于為什么會有這樣的規律，以及在探索規律過程中的經驗積累和能力提升，則很難直接而充分地表達，也很難直接傳授和傳播，這些顯然是默會知識。相對于明確知識而言，默會知識的習得對學生思維和行為的影響更大。

因此，探索規律的教學，要讓學生真正實現從“雙基”到“四基”的跨越，就要讓這些默會知識不再繼續沉默。讓學生通過多種方式領悟和與積的奇偶性的內涵，在主動探索規律的過程中感悟探索規律的方法，積累探索規律的經驗，應是本節課的教學重點和難點。基于以上認識，筆者對這節課進行了如下建構，也嘗試著對“探索規律”教學的規律進行了梳理和總結。

一、規律肯定是“藏”起來的

課始，創設懸疑情境：班級圖書角一本新書有一頁被撕掉了，借閱者小杰說他清楚記得被撕掉的那一張正反兩頁的頁碼和是138，他完全沒必要把它撕下來。小杰說謊了嗎？

生1：我覺得不是小杰撕的，他都能背下來頁碼，確實沒有必要再撕下來。（很多學生點頭表示贊同）

生2：我感覺小杰說謊了，他說正反兩頁的頁碼和是138，我算了算，好像沒有兩個連續自然數加起來的和是138。

生3：我也發現了，正反兩頁一個是奇數，一個是偶數，奇數加偶數的和一定是奇數，不可能是偶數。

師：你們能從數學的角度思考這個問題，非常好！兩個自然數的和是奇數還是偶數，其中確實蘊藏著一些規律，今天這節課我們就一起來研究和與積的奇偶性。（板書課題）

規律是事物之間內在的必然聯系，它決定著事物發展的趨向。規律往往“躲藏”在現象背后，需要深入挖掘才會浮現出來。因此，如何讓學生由表及里、自然而然地生發探索規律的欲望，往往是探索規律教學的關鍵。在本節課之前，學生對于加法和乘法算式，更多關注的是和與積的結果，而很少關注和與積的奇偶性，更不會發現和與積的奇偶性存在的規律。課始，通過創設懸疑情境，既激發了學生的學習熱情，又引入本節課的探究，讓學生的注意力很自然地從關注具體結果轉移到關注結果的奇偶性上來。

二、規律首先是“猜”出來的

師：你們覺得，兩個自然數相加的和是奇數還是偶數，與什么有關？

學生通過思考與交流，明確和的奇偶性與兩個加數的奇偶性有關，與兩個加數是質數還是合數或者兩個加數的大小無關。

師：兩個自然數相加，根據加數的奇偶性分類，一共有哪幾種情況？對于每種情況，你能提出你的猜測嗎？

生：我感覺奇數+奇數=偶數，偶數+偶數=偶數，奇數+偶數=奇數。不信的話大家可以舉一些例子進行驗證。

師：舉例驗證的確可以幫助我們很快揭開規律的面紗。下面就請同學們任意列舉一些算式，驗證自己的猜測。

牛頓曾說：沒有大膽的猜想，就做不出偉大的發現。猜想和驗證是很重要的數學研究方法，也是培養學生合情推理能力和初步的演繹推理能力的重要途徑。對于兩個加數和的奇偶性，學生可以借助之前學習所積累的經驗，很輕松地提出自己的猜測，并以一些加法算式為例，初步驗證自己的猜測。在學生充分交流并初步肯定自己的猜測之后，教師帶領學生深入思考和的奇偶性規律背后的道理，邁開了探索規律的第一步。

三、規律應該是“悟”出來的

師：剛才大家通過舉例驗證了和的奇偶性規律。但我們全班總共也就舉了一百多個例子，會不會在某個角落藏著一個算式，是不符合我們發現的規律的？我們能不能想辦法弄清它的內在道理呢？

學生先獨立思考，然后小組討論，教師組織學生交流想法。

生：我覺得不一定要列舉很多算式來證明，假設有兩筐蘋果，一筐有奇數個，一筐有偶數個，現在把兩筐蘋果兩個兩個地用紙包起來，偶數那筐正好包完，奇數那筐包到最后一定還剩一個，所以奇數加偶數的結果是奇數。

師：真聰明，不舉具體的算式了，通過生活中的例子，形象地解釋了奇數加偶數等于奇數。還有不同的想法嗎？

生：我有辦法證明奇數加奇數等于偶數，我從第一個奇數中拿出1給第二個奇數，這樣兩個數都變成了偶數，偶數加偶數結果一定還是偶數。

師：有道理，不過前提是我們要確認偶數加偶數等于偶數是正確的。誰能說服我偶數加偶數一定等于偶數？

生：偶數加偶數等于偶數不需要證明，因為第一個數是2的倍數，第二個數也是2的倍數，我們可以用乘法分配律把公因數2提取出來，所以它們的和一定是2的倍數。

生：我們小組認為，要確認和的奇偶性規律，不需要把所有的加法算式全部列舉出來。其實，一個數是奇數還是偶數是由它個位上的數字決定的，我們只要把0～9這10個數字相加的情況都列舉出來，就能證明所有的情況了。

師：大家覺得有道理嗎？通過大家剛才的交流，我們現在還需要在列舉之后再進行證明嗎？

生（齊答）：不需要！

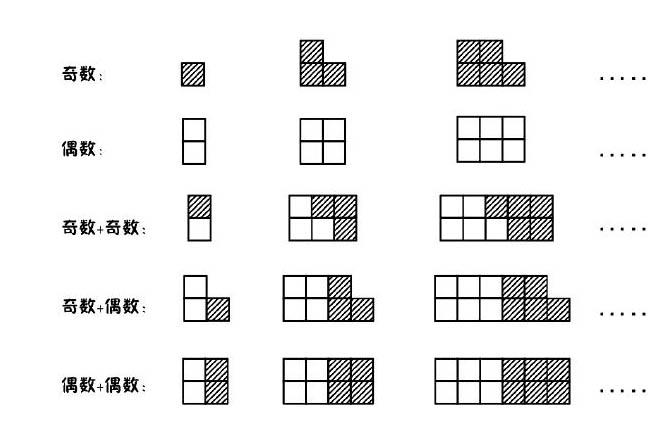
在學生充分交流的基礎上，教師課件呈現下圖，帶領學生通過數形結合再次強化對規律的內涵的理解。

學生并不難發現和的奇偶性規律，但為什么會存在這樣的規律？它的內涵是什么？則需要學生通過多種方式進行領悟，只有真正悟出了規律的內在道理，學生發現的客觀存在的規律才能真正內化為他們思維內在的規律。本環節，先讓學生討論交流，充分體驗用舉例說明、抽象、演繹等方法描述規律的過程，再通過數形結合，直觀感受規律內在的道理，通過多種方式，讓學生真正領悟規律的內涵。

四、規律可以是“用”出來的

教師接著出示：23+16+35，同桌兩人互相說一說，指名匯報。

生1：我們可以算出這3個數相加的結果，從而判斷和的奇偶性。

生2：我覺得可以運用剛才發現的兩個數相加和的奇偶性規律，先判斷出23+16的和是奇數，再判斷“奇數+35”的和是偶數。

師總結：也就是說，三個數相加，也可以通過運用兩次兩個數相加和的奇偶性規律，判斷出三個數相加和的奇偶性。

教師繼續課件出示：68+104+26、171+93+245。

生1：第一題的結果是偶數，因為前兩個偶數相加的和是偶數，第三個數還是偶數，偶數加偶數，結果還是偶數。

生2：我覺得如果再加幾個偶數，結果還是偶數，也就是說不管多少個偶數相加，結果還是偶數。

師：及時發現，及時總結，而且有理有據，真棒！第二個算式呢？

生3：第二題的結果是奇數，因為前兩個奇數相加的和是偶數，第三個數還是奇數，偶數加奇數，結果是奇數。

生4：我估計和偶數類似，不管多少個奇數相加，結果還是奇數。

生5：我不同意，比如第二題再加一個奇數，結果就變成偶數了。

生6：我發現如果一個算式中全部是奇數，關鍵要看奇數的個數，如果有奇數個奇數，結果就是奇數，如果有偶數個奇數，結果就是偶數。

師：這個猜測很大膽，能說說你的理由嗎？

生6：因為奇數個奇數，可以兩個奇數兩個奇數地配對，每一對的結果都是偶數，但最后還會多出來一個奇數，前面若干對奇數的和是偶數，偶數加最后多出來的奇數，結果一定是奇數。

師：很有道理，那偶數個奇數的結果，誰能像他一樣說清楚道理？

生7：偶數個奇數，可以兩個奇數兩個奇數地配對，每一對的和都是偶數，最后正好配完沒有剩余，不管有多少個偶數，相加的結果一定是偶數。

生8：我把他們的發現合并起來又有新的發現，一個加法算式和的奇偶性與加法算式中偶數的個數沒有關系，關鍵看這個算式中奇數的個數，如果有奇數個奇數，和就是奇數，如果有偶數個奇數，和就是偶數。

師：同學們的發現真是太精彩、太到位了！你們已經把和的奇偶性規律全部探索出來了。請大家運用你們發現的規律，判斷1+2+3+……+99+100的和是奇數還是偶數。

探索規律的教學絕不會止步于總結出規律，必須讓學生運用規律解決問題，而在運用規律的過程中，往往會有新的發現，從而豐富原有的規律，發現新的規律。這一環節，教師設計的三個連加算式，看似平淡、隨意，實際上獨具匠心、層層遞進。第一道算式讓學生明白只要掌握了兩個數相加和的奇偶性規律，就可以通過多次運用，判斷多個數相加和的奇偶性規律。第二道算式讓學生自主總結發現，無論多少個偶數相加，和一定是偶數。第三道算式讓學生先由第二道算式產生負遷移，發現錯誤的結論，再通過深入研究得出若干個奇數相加的和的奇偶性規律。在此基礎上，學生很順利地總結出任意個數相加的和的奇偶性規律。學生在用中學，在學中用，教學過程由學生的思維過程推動，規律也在運用的過程中不斷完善和豐富。

五、規律必須是“找”出來的

師：剛才，我們通過觀察、猜測、驗證、解釋和運用，發現了和的奇偶性規律。由此，你還能聯想到什么？

生：減法、乘法和除法的結果是不是也有類似的規律？

師：如果要研究積的奇偶性，你打算怎么研究？

生1：我想像研究和的奇偶性一樣，先寫幾個乘法算式，看看計算結果是奇數還是偶數，然后再尋找積的奇偶性有什么規律。

生2：我覺得規律找出來之后，還要想一想為什么會有這樣的規律。

師：看來你們不僅學會了和的奇偶性規律，還掌握了探索規律的規律，非常棒！下面就請同學們以學習小組為單位，按照剛才兩位同學所說的研究思路，探索積的奇偶性規律。

在課的最后環節，教師不再步步陪同，而是放手讓學生自己去探索積的奇偶性規律。規律只有讓學生自己“找”出來，才真正屬于他們。

數學是研究數量關系和空間形式的科學。可以說，數學學習的過程離不開對數量關系和空間形式的規律的探尋。探索規律的過程是不斷明晰數學思想方法、逼近數學本質的過程，是培養合情推理和演繹推理能力、發展創新意識和品質的過程。探索規律的教學必須首先明確規律的隱蔽性，通過激趣、猜測、驗證、領悟、運用等多個環節的“光合作用”，才能讓規律在學生心中生根、發芽，也才能讓探索規律的過程在學生以后的學習、生活中開花、結果。