臨空高速目標模糊機動檢測的IMM-EKPF算法*

付強，王剛，劉昌云，郭相科

(空軍工程大學 防空反導學院，陜西 西安　710051)

?

探測跟蹤技術

臨空高速目標模糊機動檢測的IMM-EKPF算法*

付強，王剛，劉昌云，郭相科

(空軍工程大學 防空反導學院，陜西 西安710051)

摘要：針對臨空高速目標運動狀態多變，跟蹤困難的問題，將擴展卡爾曼粒子濾波與交互多模算法相結合，提出IMM-EKPF算法，該算法不需要計算雅可比矩陣，能有效求解非線性非高斯環境的機動目標跟蹤問題。在此基礎上，有效結合模糊機動檢測，可以在目標機動和非機動之間轉換跟蹤算法，以提高跟蹤精度，減少計算量。仿真驗證該方法在臨空高速目標運動狀態多變的情況下跟蹤效果較好。

關鍵詞：臨空高速目標；信號融合；交互多模型算法；擴展卡爾曼粒子濾波；模糊機動檢測；目標跟蹤

0引言

臨空高速目標的運動狀態不固定，在機動與非機動之間不確定的變換，對穩定跟蹤技術提出巨大挑戰。擴展卡爾曼濾波(extended Kalman filter, EKF)在接近線性的模型中被經常使用，但在機動目標跟蹤中，系統及觀測模型是非高斯及非線性的，EKF算法效果不令人滿意。粒子濾波(particle filter, PF)思想是用樣本形式來描述先驗及后驗信息[1-2]，隨著樣本的增加，粒子濾波估計接近最優貝葉斯估計，但存在退化現象，一種改進的方法是選擇合理的建議分布函數[3]。在研究建議分布函數構造的基礎上，Freitas提出擴展卡爾曼粒子濾波算法[4](extended Kalman particle filter, EKPF)，可利用EKF算法，使粒子分布接近后驗概率分布，同時減少粒子的使用個數。與濾波模型一樣，機動模型的選擇也是機動目標跟蹤難題，交互多模型(interactive multiple model, IMM)算法使用馬爾可夫過程描述模型之間的切換[5]。

本文將EKPF和IMM算法相結合，提出交互多模型擴展卡爾曼粒子濾波算法(interactive multiple model-extended Kalman particle filter, IMM-EKPF)，由于不需要計算雅可比矩陣，針對非線性非高斯環境的機動目標具有很好的跟蹤效果。IMM-EKPF與EKF相比計算量過大，當臨空高速目標處于非機動時，EKF能夠在保證跟蹤精度的條件下減少計算量。既而提出結合模糊機動檢測，其思想是首先對殘差進行平滑，消除隨機誤差影響，再對平滑殘差及殘差變化值進行模糊化處理，推理目標發生機動的概率。設置機動門限，當機動概率大于門限值時，認定目標發生機動，使用IMM-EKPF，反之，使用EKF。

本文方法能夠在確保跟蹤精度的前提下減少計算量，針對臨空高速目標有很好的適用性。

1EKPF算法

標準的粒子濾波最常見的問題就是粒子退化問題，避免退化的方法主要是重采樣算法[6]。這里采用粒子濾波和擴展卡爾曼結合的算法，即考慮到最近觀測信息的影響。

EKPF依據蒙特卡羅方法，通過使用一定的加權粒子來擬合狀態空間中狀態向量服從的概率密度函數，并且通過貝葉斯理論使用觀測值修正加權粒子的權值，最優狀態估計值為粒子的加權求和，把方差和最優估計值傳給擴展卡爾曼濾波方程完成處理，對濾波精度有整體的提高[7]。

設初始狀態變量x0服從p(x0)分布，EKPF算法流程如下：

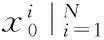
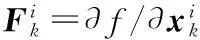
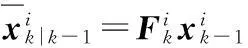
(1)

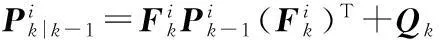
(2)

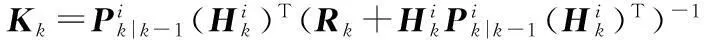
(3)

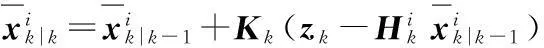
(4)

(5)

Step 3： 根據公式計算N個粒子對應的權值，并且將這些粒子的權值做歸一化處理；

Step 4： 通過重采樣計算得出重采樣后的粒子和權值；

Step 5： 分別計算每個粒子相應的方差矩陣和狀態變量的最優估計；

Step 6： 將Step 4中完成重采樣的粒子及Step 5中計算得出的方差陣代入到Step 2中完成迭代運算。

2IMM-EKPF算法

在機動目標跟蹤算法中，交互多模型算法是一種性能較好的算法，因為多種模型的交互作用，使得目標在做不同形式的運動時，可以更好的符合其真實狀態。將擴展卡爾曼粒子濾波與交互多模算法相結合，可以適應于非線性非高斯環境的機動目標跟蹤。算法循環包括：交互運算、濾波、更新模型概率以及融合輸出等[8]。

(1) 交互運算

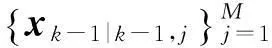
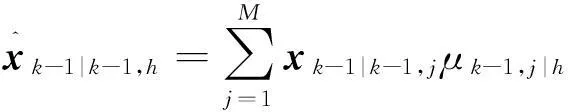
(6)

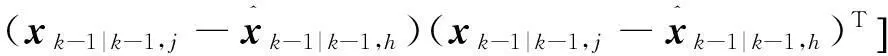
(7)

(2) 濾波

粒子預測

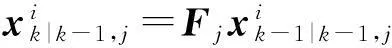
(8)

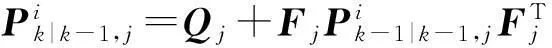
(9)

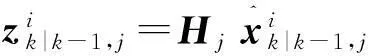
(10)

計算殘差

(11)

(3) 模型概率更新

計算模型的似然函數

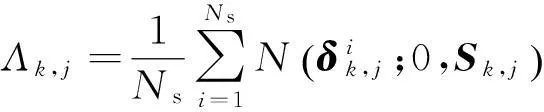
Sk,j=

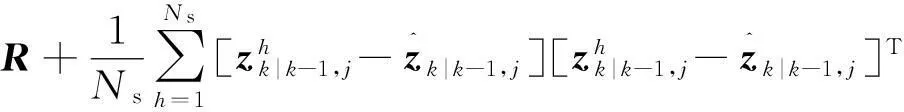
(12)

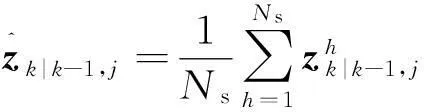
(13)

各模型概率更新

(14)

(4) 融合輸出

(15)

3基于平滑殘差的模糊機動檢測

臨空高速目標實際運動狀態在機動及非機動2種模式之間變化，一般可以用多個機動模型和一個非機動模型來描述，如圖1所示。通常濾波算法的跟蹤性能與使用的模型和實際運動狀態的匹配程度有很大關系。

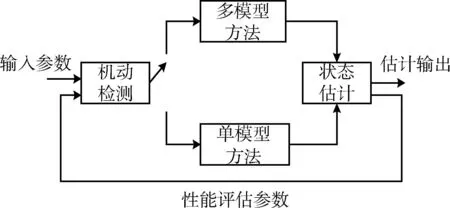
圖1　改進算法示意圖Fig.1　Schematic diagram of improved algorithm

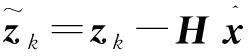
圖2某一機動目標跟蹤中各個時刻的殘差值加權。由于參數及系統噪聲等不確定性因素的影響，使得原始殘差值波動范圍較大，導致機動檢測有很多誤判斷。

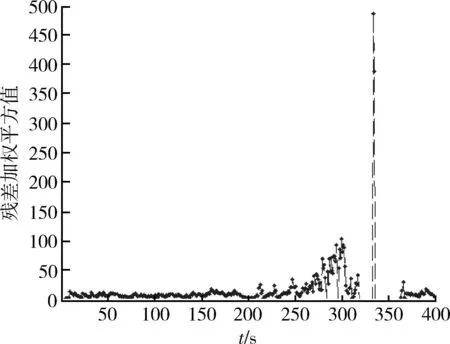
圖2　加權平方后的殘差值Fig.2　Residual value of the weighted square

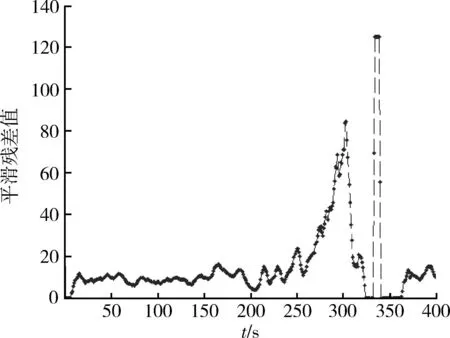
圖3　平滑殘差值Fig.3　Smoothed residuals

圖4為殘差平滑前及平滑后的比較。可見，平滑方法能夠較好的消除了隨機誤差帶來的影響，可以較好的體現機動特性。

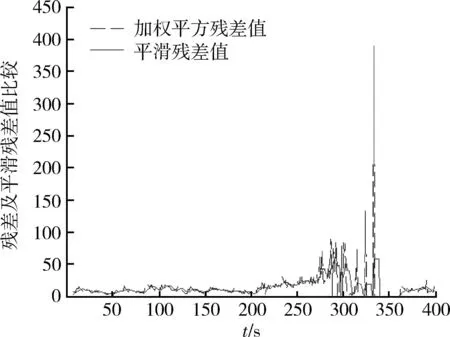
圖4　殘差平滑前后值比較Fig.4　Comparison of residual smoothing

對于平滑殘差，能夠較好避免隨機檢測的錯誤，然而普遍存在比較明顯的滯后效應，即目標發生機動一段時間后，殘差值才超過門限值。這一點影響了跟蹤性能，當目標進行強機動時，較大的延時通常會使丟失目標[11]。

通過平滑殘差曲線能夠看出，目標在發生機動之前，數值較為穩定的隨機波動，當目標機動時，平滑殘差值在不斷增加，直到大于門限。雖然需要一段時間平滑殘差值才能超過門限，但在機動開始后，平滑殘差值是一直增加的且變化規律較為穩定[12]。

若在算法中將此判斷信息引入，對提高機動跟蹤的準確性和實時性有明顯幫助，這一思想可以通過模糊推理過程來實現。

在整個算法中，用模糊推理來進行機動跟蹤，依據當前殘差變化和平滑殘差值，算出該時刻使用IMM-EKPF的概率，當此概率大于設定的門限時，使用IMM-EKPF，否則使用EKF。

3.1模糊化平滑殘差

首先將輸入變量完成模糊化，算法中輸入包括當前平滑殘差ek以及平滑殘差的變化dek。平滑殘差ek可以通過計算移動窗口的平均殘差值得到[13]， dek=ek-ek-1為平滑殘差變化值，dek如圖5所示。將平滑殘差變化值以及平滑殘差做模糊化處理，殘差變化值的模糊集合定義為：負、零、正；平滑殘差值的模糊集合定義為：小，中，大。隸屬度函數為梯形，如圖6所示。

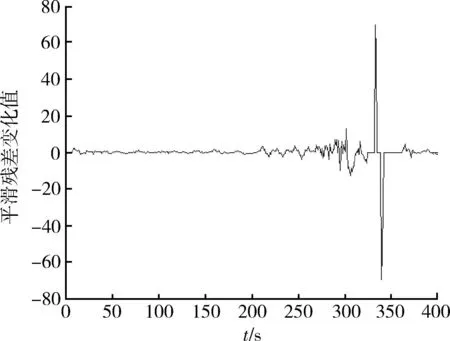
圖5　平滑殘差變化值圖Fig.5　Smoothed residual variation chart

圖6　梯形隸屬度函數Fig.6　Trapezoidal membership function

3.2模糊推理與解模糊

模糊推理采用TS方法，對于2輸入1輸出系統的模糊控制規則，其基本形式為

ifekisAand dekisB,thenp=C

平滑殘差以及殘差變化值的模糊集合分別為A,B，目標機動的概率值為C。

顯而易見，當平滑殘差的模糊變量為“大”并且殘差變化的模糊變量為“正”時，機動的概率最大，可設為1，其他情況可以此邏輯類推。通過輸入的殘差、殘差變化量和隸屬函數可以得到如表1所示的模糊推理規則，P(k)為目標機動的概率。

表1　模糊推理規則

4帶模糊機動檢測的跟蹤算法

使用模糊機動檢測，使得跟蹤算法可以在機動和非機動之間轉換，檢測到機動時，使用IMM-EKPF算法，以提高機動時的跟蹤精度；而非機動時，采用普通的EKF算法，在保證跟蹤精度的情況下，盡量減少計算量。算法的整體流程圖如圖7所示。

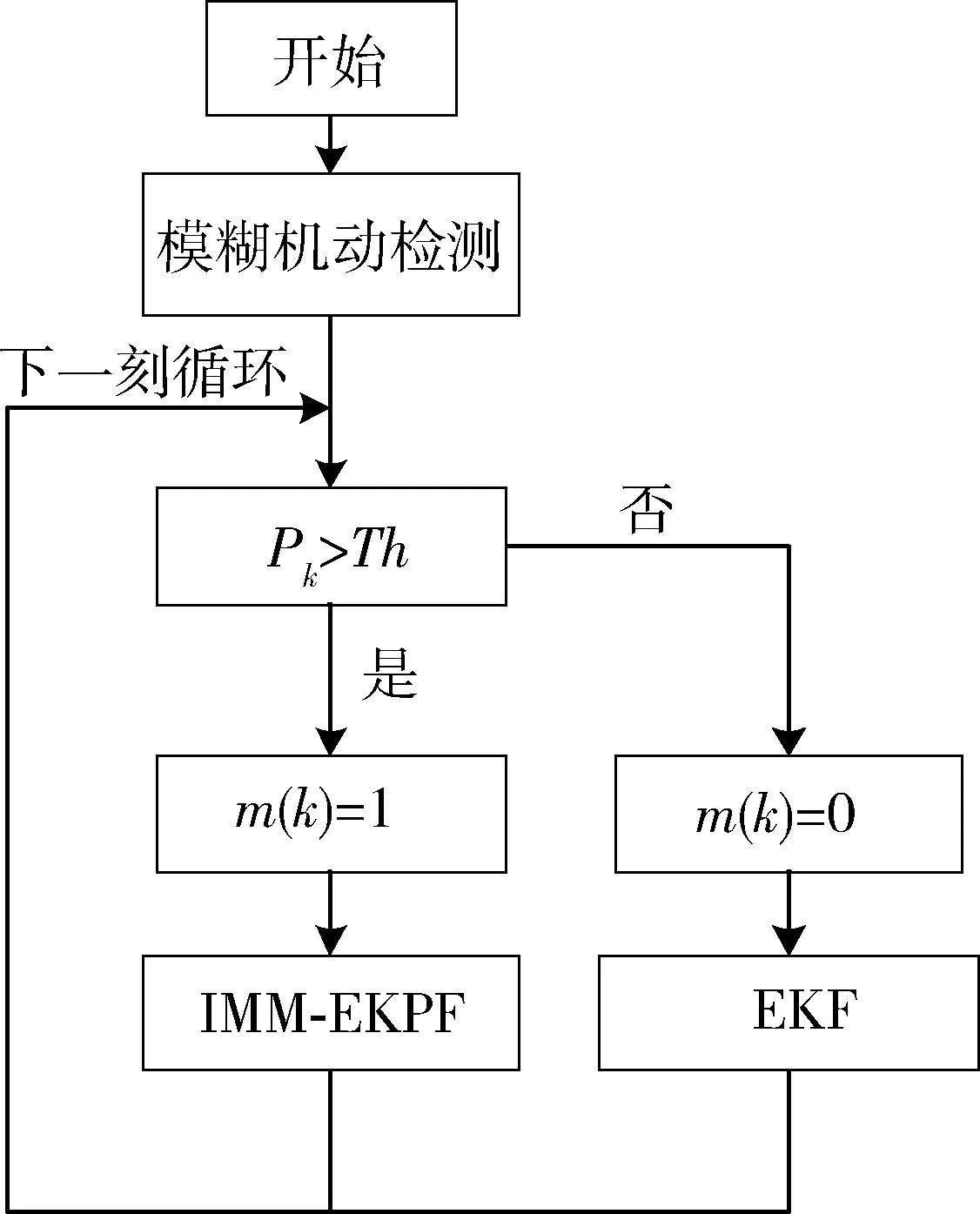
圖7　算法流程圖Fig.7　Algorithm flow chart

為了驗證濾波跟蹤算法的有效性，現使用Matlab對其進行仿真。假設算法中采用的量測方程和狀態方程為

(16)

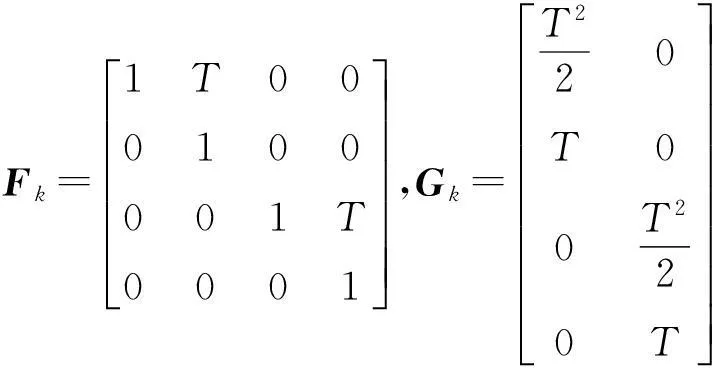
設采樣周期T為2，檢測機動的有效窗口長度為5，門限值Th為0.6[15]，粒子數目為50，進行50次蒙特卡羅仿真。本文的仿真選取弱機動和機動的情況進行仿真實驗。首先假設目標的運動狀態如表2所示。目標的初始位置是(2 000，10 000)，進行勻速運動和勻加速運動的交替運動，速度和加速度都很小，機動性較弱。

由以上假設進行仿真，其中圖8表示目標的真實軌跡與觀測軌跡，圖9表示殘差值、殘差平滑的對比，圖10表示平滑殘差值的變化值，圖11表示每個時刻模糊推理得到的機動概率結果，圖12表示目標真實軌跡與50次濾波軌跡的比較結果。

由目標的運動狀態可知，在采樣時間為200時，目標加速機動，在之后的時間段內，都處于機動狀態，直到時間為330左右，才恢復勻速運動。由模糊機動檢測得到的機動概率值在目標加速時有所體現，但是值不大，表明目標正在進行的是弱機動，由圖11模糊推理結果可知，本文算法得到的機動檢測結果是可信的。

表2　目標真實運動狀態

圖8　真實軌跡與觀測軌跡Fig.8　True trajectory and observation trajectory

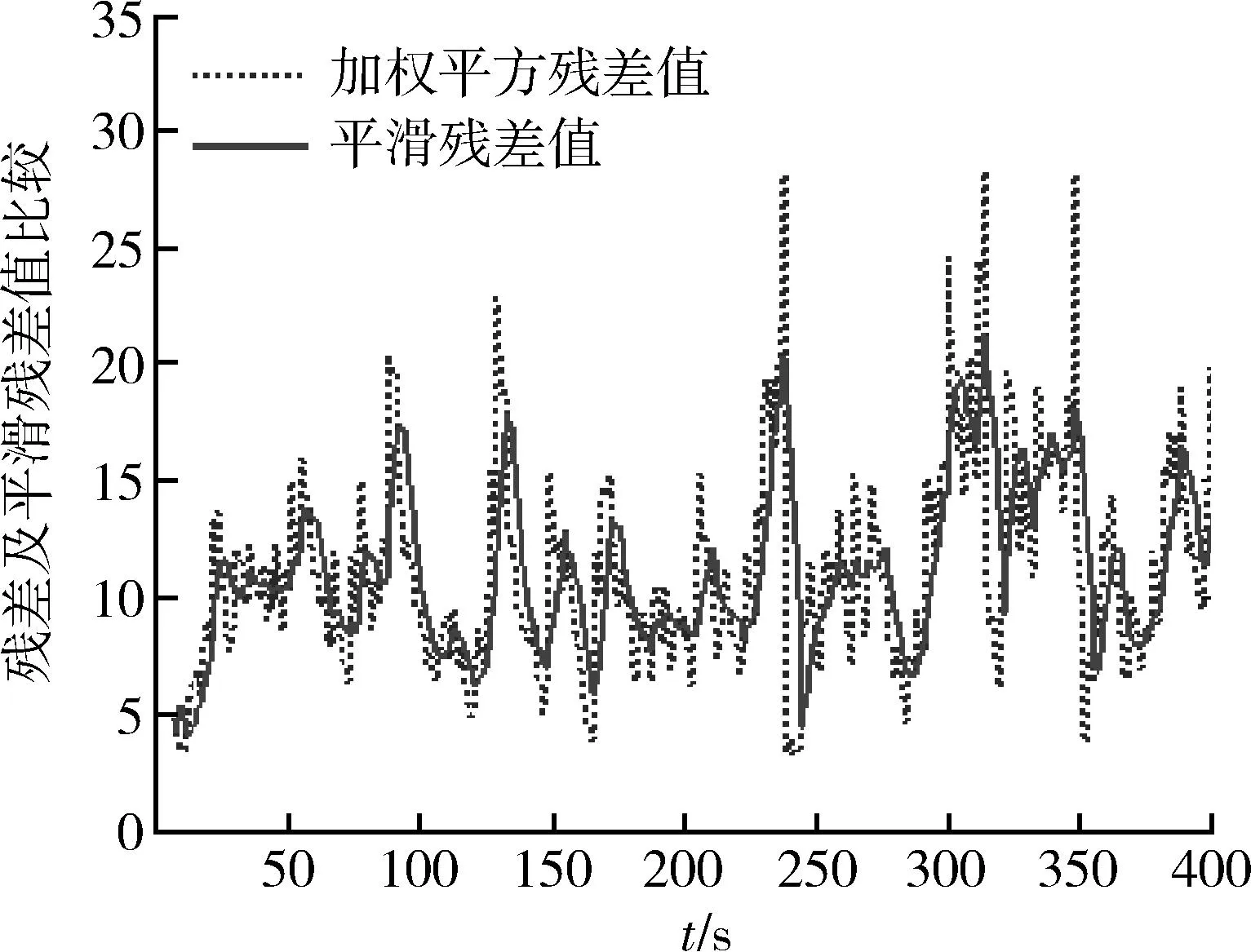
圖9　加權平方殘差及平滑殘差值比較Fig.9　Comparison of weighted squared residuals and smoothed residuals

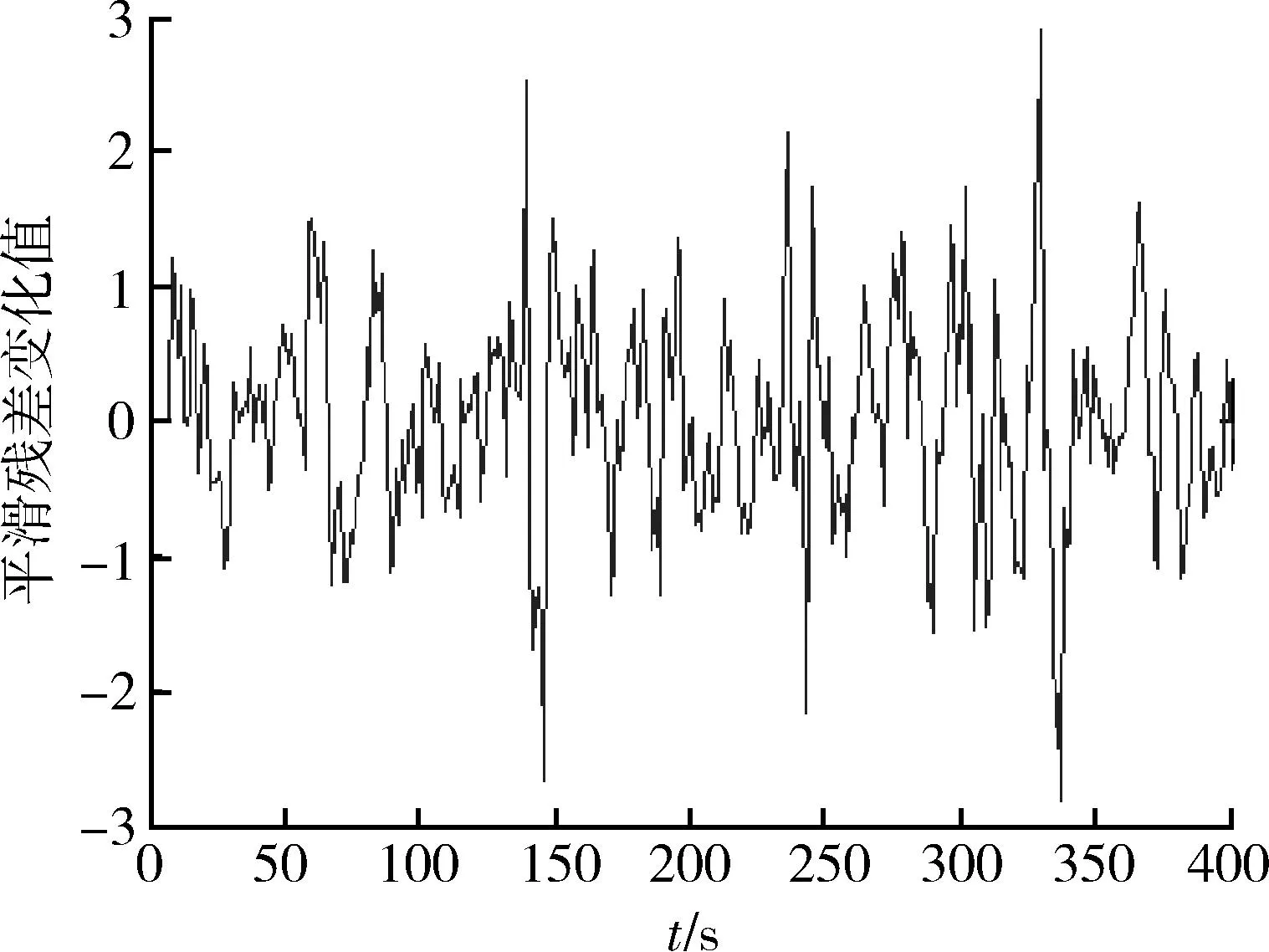
圖10　平滑殘差變化值Fig.10　Smoothed residual variation

圖11　任意時刻模糊推理結果Fig.11　Fuzzy reasoning results at any time

由圖12可以看出本文方法適用性較好，在目標強機動時濾波軌跡會產生一定偏差，但很快就與真實軌跡擬合。

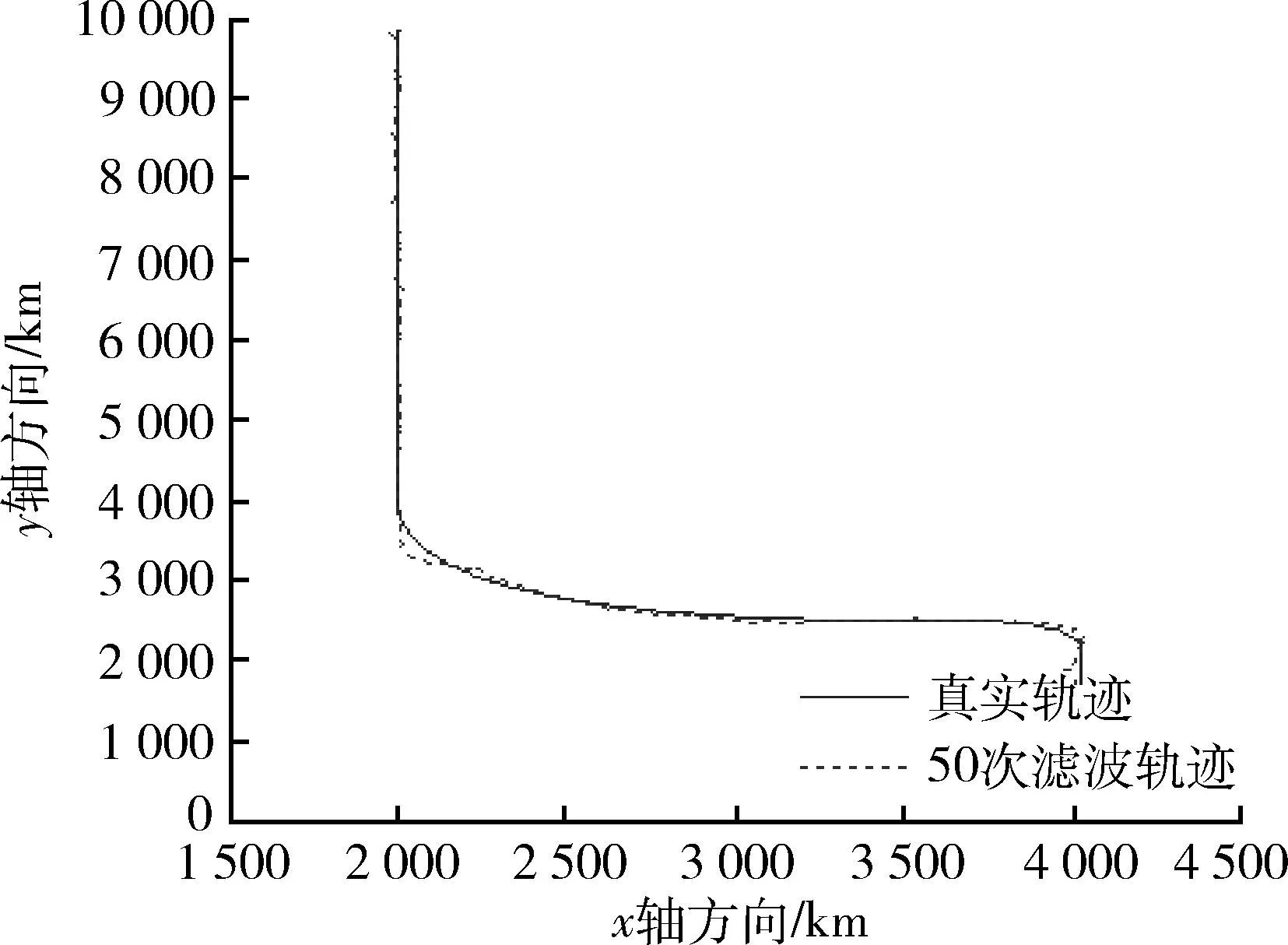
圖12　真實軌跡與濾波軌跡比較Fig.12　Comparison between real and filtered navigation

本文選取做轉彎機動的目標進行對機動情況濾波效果的檢測。假設目標運動狀態如表3所示，進行仿真。本例的目標狀態相對上例，機動性較強。圖13表示殘差值、殘差平滑值，圖14表示平滑殘差值的變化值，圖15表示x和y坐標的濾波誤差均值曲線及標準差曲線，圖16表示真實軌跡與50次濾波軌跡的比較。

表3　目標真實運動狀態

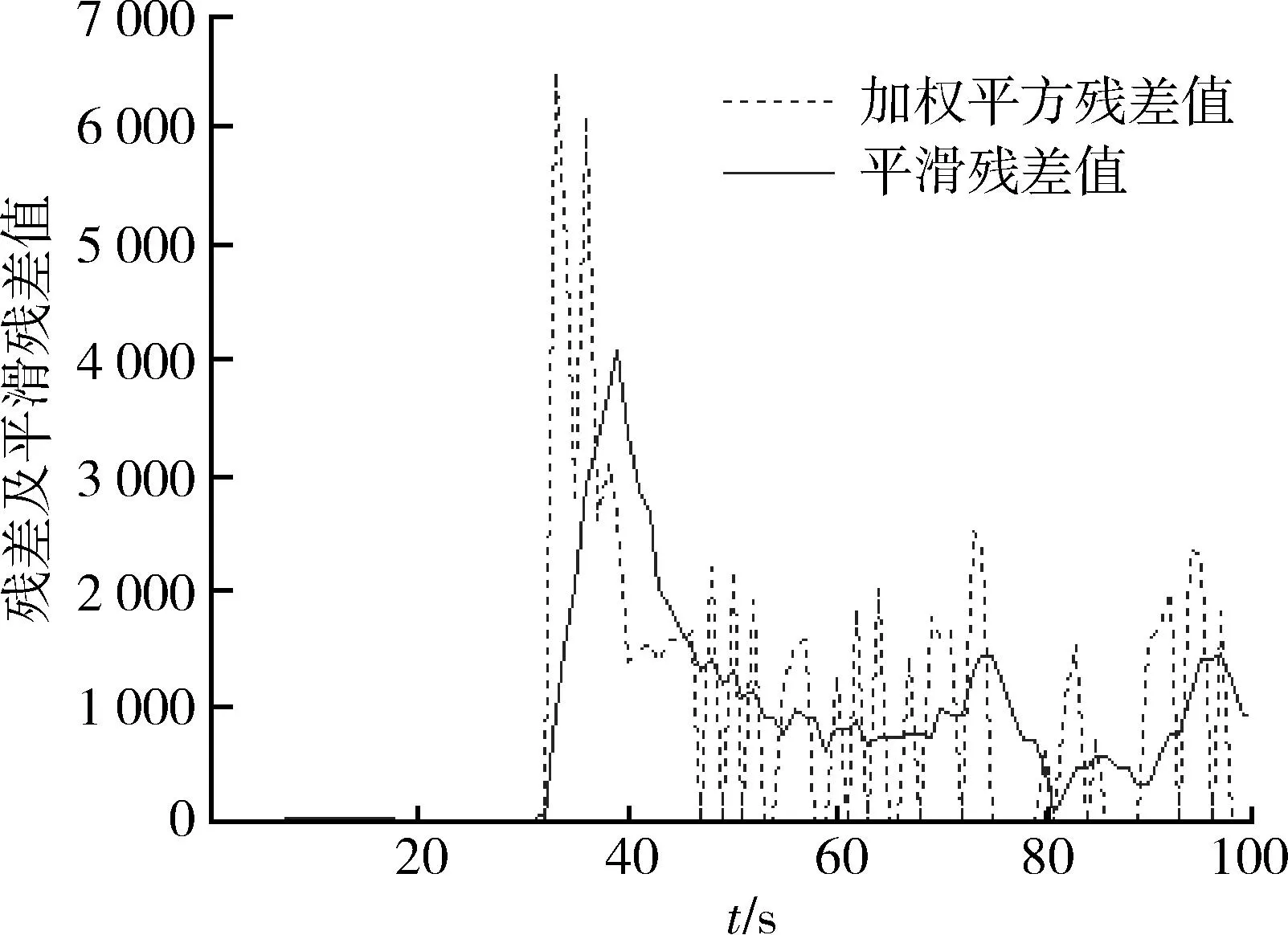
圖13　殘差及平滑殘差值Fig.13　Residuals and smoothed residuals

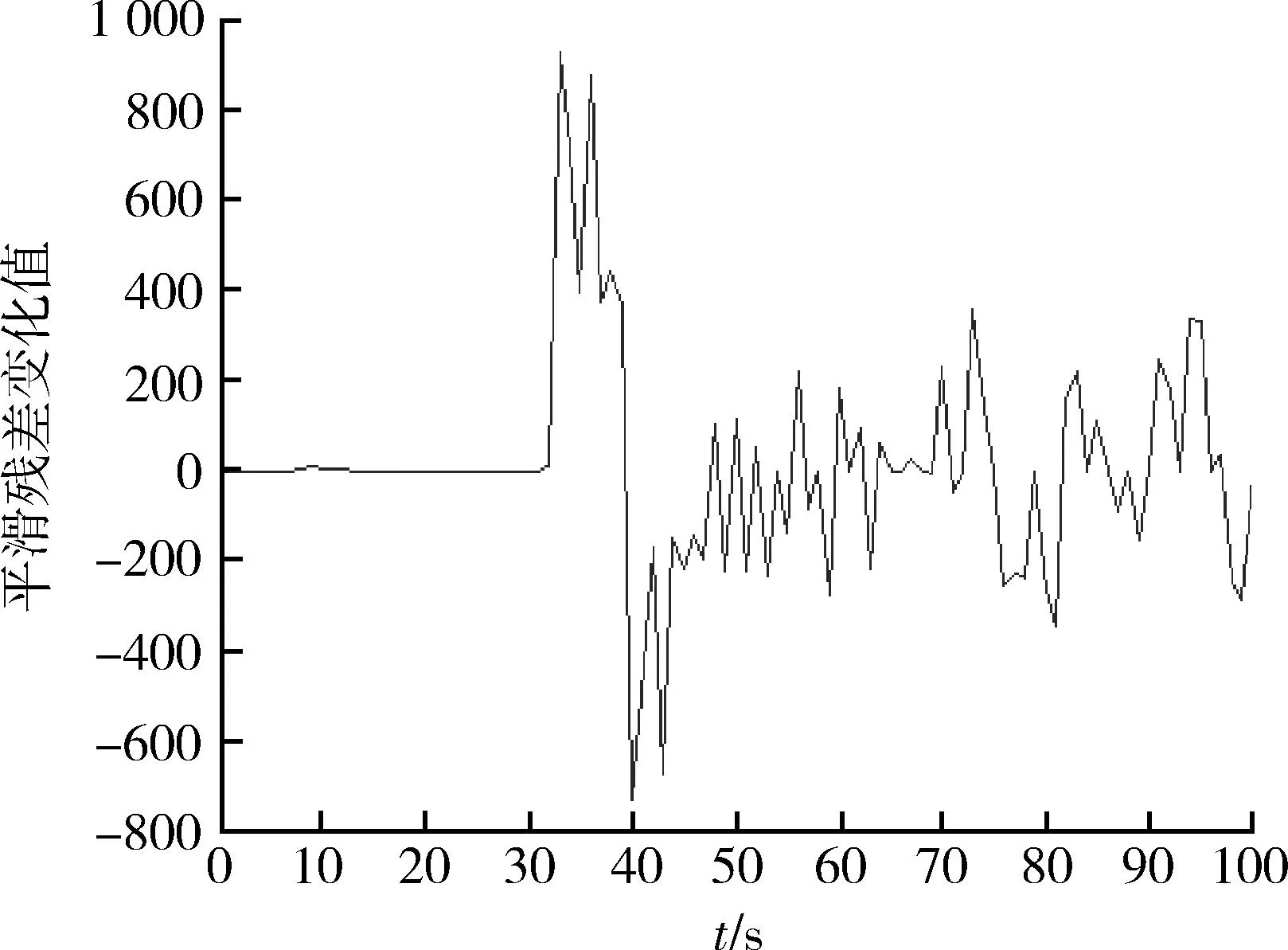
圖14　平滑殘差變化值Fig.14　Smoothed residual variation

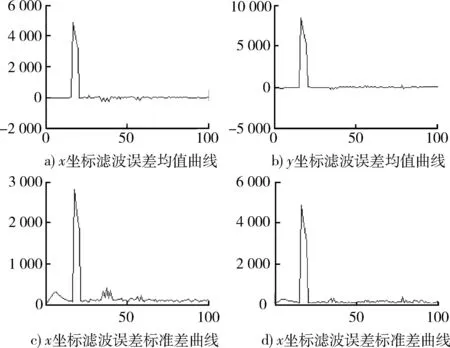
圖15　x和y坐標濾波誤差均值及標準差曲線Fig.15　x and y coordinates of the filter error mean and standard deviation curve

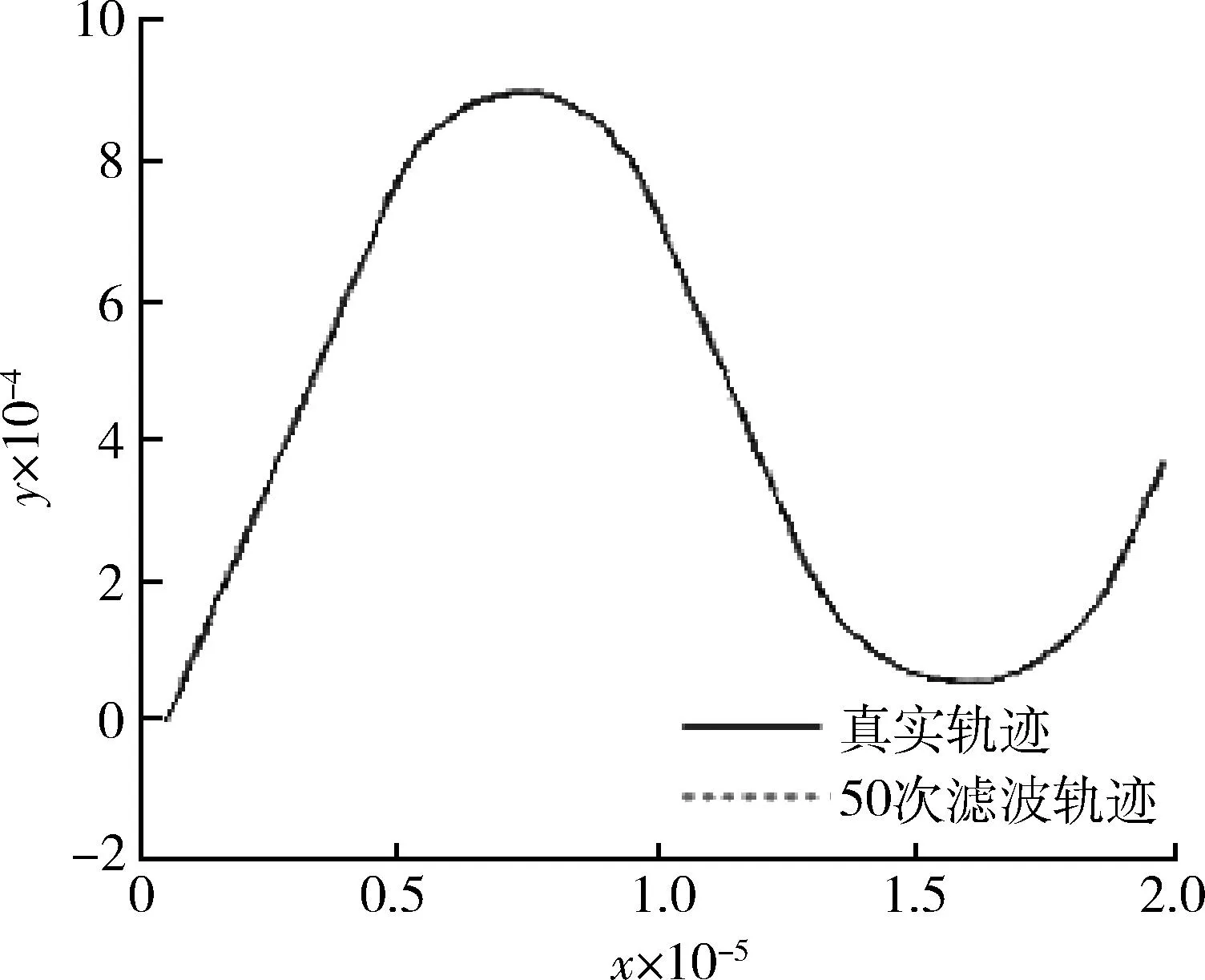
圖16　真實軌跡與濾波軌跡比較Fig.16　Comparison between real trajectory and filter trajectory

由圖16可以看出，經過50次濾波后的軌跡與真實軌跡非常逼近，目標勻速轉彎時能夠穩定跟蹤，有效驗證了結合模糊機動的IMM-EKPF算法在臨空高速目標跟蹤中具有很好的性能。

5結束語

本文首先將平滑殘差進行模糊推理，判定目標是否機動。當目標機動時，提出IMM-EKFP算法，該算法能有效解決非高斯非線性環境下目標跟蹤問題，目標不機動時，運用傳統EKF算法，保證跟蹤性能的前提下減少計算量。最終通過真實航跡與濾波航跡的比較，驗證該方法針對臨空高速目標跟蹤效果顯著。

參考文獻：

[1]WANG X, CHEN J F, SHI Z G, et al. Fuzzy-Control-Based Particle Filter for Maneuvering Target Tracking[J]. Progress In Electromagnetics Research,2011, 118(3): 1-15.

[2]FARAHMAND S, ROUMELIOTIS S I, GIANNAKIS G B. Set-Membership Constrained Particle Filter: Distributed Adaptation for Sensor Networks [J].IEEE Transactions on Signal Processing, 2011, 59(9): 4122-4138.

[3]HUANG Jin-wang，FENG Jiu-chao. Signal Reconstruction in Wireless Sensor Networks Based on a Cubature Kalman Particle Filter[J]. Chinese Physics B, 2014, 36(7): 1213-1216.

[4]李鋒, 解少飛, 畢志獻. 高超聲速飛行器中若干氣動難題的實驗研究[J]. 現代防御技術, 2014, 42(5): 369-375.LI Feng,XIE Shao-feng,BI Zhi-xian. Experimental Study on Aerodynamic Problems of High-Speed Vehicle[J].Modern Defense Technology,2014, 42(5):369-375.

[5]LIAO T, STUTZLE T, de Oca M A M. A Unified Ant Colony Optimization Algorithm for Continuous Optimization[J]. European Journal of Operational Research, 2014, 234(3):597-609.

[6]LI X R, JILKOV V P. A Survey of Maneuvering Target Tracking Part V: Multiple-Model Methods[J].IEEE Trans. on Aerospace and Electronic Systems,2005, 41(4): 1255-1321.

[7]侯靜, 景占榮, 羊彥. 遠距離干擾環境下目標跟蹤的擴展卡爾曼粒子濾波算法[J].電子與信息學報, 2013, 35(7): 1587-1592.

HOU Jing,JING Zhan-rong,YANG Yan. Extended Kalman Particle Filter Algorithm for Target Tracking in Stand-off Jammer[J].Journal of Electronics & Information Technology, 2013, 35(7): 1587-1592.

[8]王華劍. 基于改進擴展卡爾曼粒子濾波的目標跟蹤算法[J].計算機應用研究, 2011, 28(5): 1634-1639.

WANG Hua-jian. Target Tracking Algorithm Based on Improved Extend Kalman Particle Filter[J]. Application Research of Computers, 2013, 35(7): 1587-1592.

[9]江寶安,萬群. 基于UKF-IMM的雙紅外機動目標跟蹤算法[J]. 系統工程與電子技術, 2008, 30(8): 1454-1459.

JIANG Bao-an,WAN Qun. Maneuvering Target Passive Tracking with Dual Inferred Observer Using IMM Algorithm Based on UKF[J]. Systems Engineering and Electronics, 2008, 30(8): 1454-1459.

[10]MOHAMMADI A, ASIF A. Consensus-Based Distributed Unscented Particle Filter[C]∥IEEE Statistical Signal Processing Workshop (SSP), Nice, 2011: 237-240.

[11]YANG W, FU Y W, LI X. Joint Target Tracking and Classification Via RFS-Based Multiple Model Filtering [J].Information Fusion, 2013, 18(3), 101-106.

[12]徐洋, 徐松濤, 羅文濤. 基于虛擬檢測函數下的IMM-UKF機動目標跟蹤[J]. 火力與指揮控制, 2015, 40(1): 37-41.

XU Yang,XU Song-tao,LUO Wen-tao.IMM-UKF Maneuvering Target Tracking Based on Virtual Detection Function[J]. Fire and Command Control, 2015, 40(1): 37-41.

[13]EN F, WEI X X, ZONG X L. Maneuvering Target Tracking Using Fuzzy Logic-Based Recursive Least Squares Filter [J]. EURASIP Journal on Advances in Signal Processing, 2014, 53(1):1-9.

[14]Ahmadreza, Amirzadeh, Ali Karimpour. An Interacting Fuzzy-Fading-Memory-Based Augmented Kalman Filtering Method for Maneuvering Target Tracking[J]. Digital Signal Processing,2013, 23(5): 1678-1685.

[15]DONG L P, YUN F G. Fuzzy-Logic Adaptive Variable Structure Multiple-Model Algorithm for Tracking a High Maneuvering Target[J]. Journal of the Franklin Institute，2013, 21(9)：11-21.

Near Space High-Speed Targets Fuzzy Maneuvering Detection with IMM-EKPF Algorithm

FU Qiang, WANG Gang, LIU Chang-yun, GUO Xiang-ke

(AFEU, Air and Missile Defense College, Shaanxi Xi’an 710051, China)

Abstract:Aiming at the issue that it is difficult to trace variable motion states of near space high-speed targets, the extend Kalman particle filter (EKPF) and interaction multiple model (IMM) are combined to develop an interaction multiple model-extend Kalman particle filter (IMM-EKPF) algorithm. The algorithm needs not to calculate the Jacobi matrix, and it can effectively solve non Gauss and non-linear target trace. On this basis, combined with fuzzy maneuvering detection, rack algorithm is transitioned between maneuvering and non-maneuvering to improve the tracking accuracy and reduce the amount of calculation. Results demonstrate the feasibility of this method.

Key words:near space high-speed target; signal fusion; interaction multiple model; extend Kalman particle filter; fuzzy maneuvering detection; target trace

*收稿日期：2015-04-20；修回日期：2015-07-07

基金項目：國家自然科學基金項目(61272011); 國家自然科學青年基金(61102109)

作者簡介：付強(1988-)，男，陜西西安人。博士生，主要研究方向為智能信息處理。

通信地址：710051陜西省西安市長樂東路空軍工程大學防空反導學院E-mail：fuqiang_66688@163.com

doi:10.3969/j.issn.1009-086x.2016.02.023

中圖分類號：TN957.51；TP391.9

文獻標志碼：A

文章編號：1009-086X(2016)-02-0143-08