循環流化床鍋爐床溫的預估滑模控制

朱紅霞，　沈　炯，　李益國

(1． 東南大學 能源與環境學院， 南京 210096； 2． 南京工程學院 能源與動力工程學院， 南京 211167)

?

循環流化床鍋爐床溫的預估滑模控制

朱紅霞1,2，沈炯1，李益國1

(1． 東南大學 能源與環境學院， 南京 210096； 2． 南京工程學院 能源與動力工程學院， 南京 211167)

摘要：針對大慣性、大滯后熱工過程因負荷、煤種和環境條件的改變以及模型簡化等帶來的不確定性，設計了一種便于運行人員理解和工程實現的預估滑模控制方案.首先基于標稱工況下辨識得到的二階加純滯后(SOPDT)模型，構建一個無遲延輸出預估模型，用于過程輸出值的預測，然后通過合理設計滑模函數和不確定上界自適應估計的滑模控制律，使得具有不確定性的閉環系統能在任何外擾的作用下保持漸進穩定.針對循環流化床鍋爐床溫對象的仿真實驗結果表明：采用該預估滑模控制方案的床溫控制系統調節速度快、超調量小且具有很強的抗干擾能力.

關鍵詞：預估滑模控制； SOPDT模型； 不確定性； 循環流化床； 床溫

由于循環流化床(CFB)鍋爐具有燃燒效率高、燃料適應性廣和低污染等優點[1]，因而近年來在國內外受到廣泛重視，并得到迅速發展.CFB鍋爐在動態特性上不同于煤粉爐和重油爐，主要表現在鍋爐燃燒室內流化層大容量的熱平衡特性.床層溫度是直接影響CFB鍋爐能否安全連續運行的重要控制參數，為保證鍋爐處于最佳燃燒條件，運行時床溫一般控制在850～950 ℃，此時爐內脫硫效率高且NOx的生成量小.目前，工程上CFB鍋爐床溫控制系統大多采用傳統的PID控制方法；理論研究方面，模糊控制[1-2]、自抗擾控制[3]和預測控制[4-5]等先進控制方法已被應用到床溫控制中.

采用CFB鍋爐的機組一般均會直接參與調峰，因而會頻繁變負荷運行.一些電廠在煤炭供應緊張期間，其燃料來源多樣化，導致煤質經常發生變化.運行工況的調整、煤質的變化、環境的改變以及控制系統設計中對模型的簡化和近似等，都不可避免地給系統帶來各種不確定性，而且這些不確定性還會隨著系統動態的演化而改變，從而嚴重影響控制系統的實際性能.應對不確定性的影響，一種可行的控制策略是采用魯棒控制，但目前采用較多的H∞魯棒控制等方法理論性較強，不利于運行人員的理解和工程實現.滑模控制(SMC)是一種特殊的魯棒非線性控制器，由于滑動模態可以進行設計且與對象參數及擾動無關，所以SMC具有響應快速、對參數變化及擾動不靈敏、無需系統在線辨識和物理實現簡單等優點[6-7].鑒于滑模控制在處理不確定性和抗干擾方面的絕對優勢，筆者針對CFB鍋爐床溫等復雜熱工對象，從便于工程實際應用的角度出發，設計了一種簡單而新穎的預估滑模控制方案，并通過仿真實驗驗證了其有效性.

1CFB鍋爐床溫被控對象的動態特性

CFB鍋爐運行過程中影響床溫的因素很多，如給煤量、一次風量、二次風量、石灰石量、排渣量和返料量等.目前，國內的CFB鍋爐主要通過給煤量和一次風量進行床溫調節.仇韜[8]以金陵石化熱電廠的6號爐(220 t/h循環流化床鍋爐)為試驗對象，在不同負荷和不同煤種情況下對其動態特性進行了分析，并給出不同工況下的床溫對象模型.

給煤量-床溫通道的傳遞函數(未考慮給煤的傳輸遲延)為：

(1)

一次風量-床溫通道的傳遞函數為：

(2)

式中：KB和KF均為靜態增益；τB、TB、τF和TF為時間常數，均隨運行工況的不同而變化.

仇韜[8]通過相關性分析和不同工況下的仿真計算，建立了式(1)和式(2)中的各參數與負荷和煤種性能指數之間的關系，利用函數關系可以直接根據負荷和煤質確定出當前工況下CFB鍋爐床溫對象的傳遞函數模型.但其提供的模型未考慮燃料的傳輸遲延.若考慮傳輸遲延，給煤量-床溫通道的動態特性可表示為：

(3)

式中：τ0為給煤量在傳輸環節的遲延時間，s.根據實際經驗，近似估計τ0=30 s.

表1給出了CFB鍋爐在90%、80%和70% 3個不同負荷下分別采用大同煙煤、陽山無煙煤和興隆褐煤時床溫的傳遞函數模型參數.圖1給出了在不同負荷和不同煤種下，給煤量階躍擾動和一次風量階躍擾動下床溫的動態響應特性.

表1　不同負荷下CFB鍋爐采用不同煤種時床溫的傳遞函數模型參數

(a)給煤量階躍增加(b)一次風量階躍增加

圖1不同工況下CFB鍋爐床溫的階躍響應曲線

Fig.1Step response of bed temperature of CFB boiler at different operating points

從圖1可以看出，給煤量階躍增加時，床溫先下降，再逐漸上升到新的平衡狀態.一次風量階躍增加時，床溫在短時間內先上升，再逐漸下降到新的平衡狀態.床溫在初始階段具有逆響應特性，這給控制系統的設計帶來困難.而且負荷的變化會顯著影響CFB鍋爐床溫的動態特性.如低負荷時給煤量-床溫的靜態增益高于高負荷時的靜態增益，并且低負荷時床溫的動態響應時間比高負荷時稍長.低負荷時一次風量-床溫的靜態增益高于高負荷時的靜態增益，并且低負荷時床溫的動態響應時間比高負荷時要短.此外，煤質的變化也會影響床溫的動態特性,如低位發熱量較高的大同煙煤對應的給煤量-床溫靜態增益要高于低位發熱量較低的興隆褐煤對應的給煤量-床溫靜態增益.

2基于SOPDT模型的預估滑模控制方案

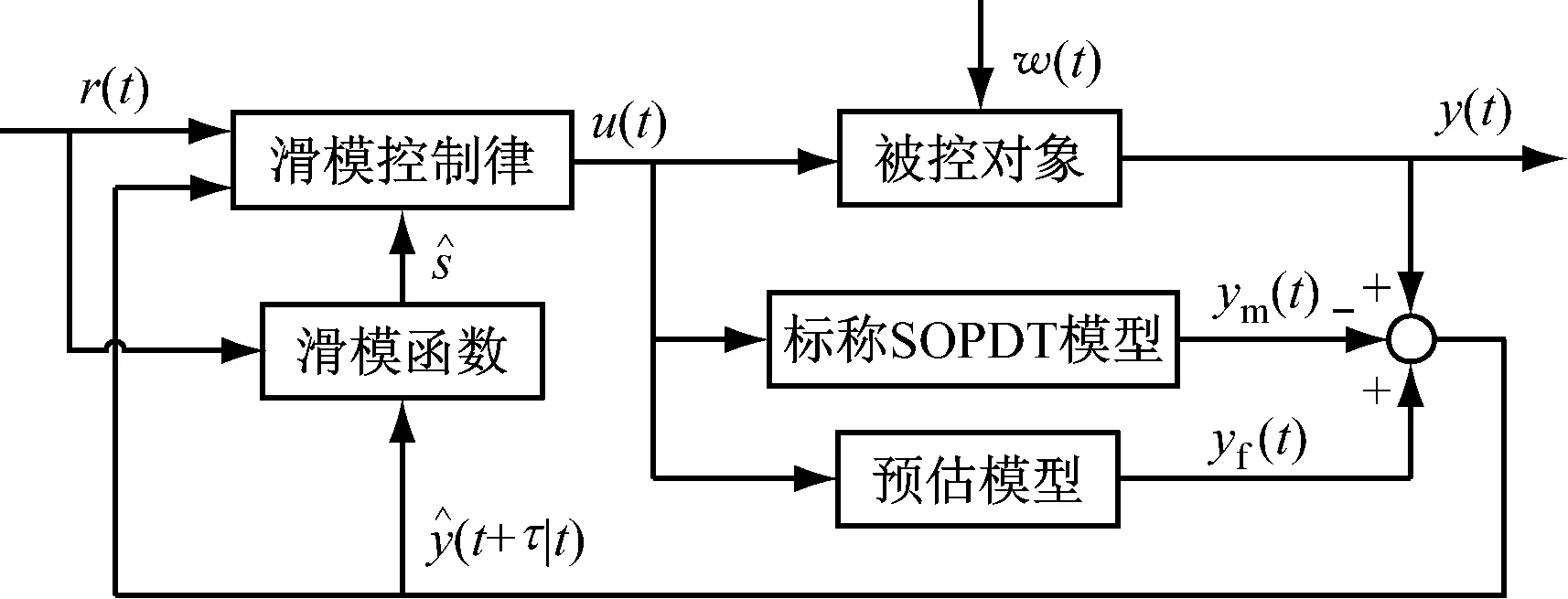
圖2　基于SOPDT模型的預估滑模控制方案

2.1基于SOPDT模型的預估模型

工程上,通常用一階加純滯后(First-order Plus Dead-time，FOPDT)模型或二階加純滯后(SOPDT)模型描述被控對象的動態特性.相比于FOPDT模型，SOPDT模型具有更廣泛的適用性，采用SOPDT模型近似逼近高階對象得到的精度通常很高，足以滿足生產過程中控制器設計對模型精度的要求，因此，筆者基于SOPDT模型設計滑模控制器.

假定在標稱工況下辨識得到被控對象的SOPDT傳遞函數模型為：

(4)式中：K、T、ζ和τ分別為穩態增益、自然振蕩周期、阻尼系數和過程的遲延時間；a1=1/T2，a2=2ζ/T，b1=K/T2.

對應的二階微分方程為：

(5)

式中：u和ym分別表示標稱模型的輸入和輸出.

將遲延時間τ從式(5)中移除，可得無遲延預估模型：

(6)

式中：yf(t)為利用無遲延模型得到的超前一個遲延時間段τ(即t+τ時刻)的輸出估計值.

為了能夠在有建模誤差和未測干擾時提高預測的準確性，實際應用時可通過式(7)對過程輸出預測值進行修正.

(7)

2.2滑模控制器設計

一般的熱工調節問題，要求被控對象的被控變量y(t)能夠跟蹤其期望的設定值信號r(t)，并能抑制各種干擾對系統輸出的影響.因而，控制器設計的目的是使實際輸出能夠跟蹤其設定值或維持在其設定值附近，使得誤差趨近于零.

考慮一個不確定模型：

(8)

式中：d(t)為被控過程總的不確定性，包括參數不確定性和外部干擾.假定d(t)是有界的，|d(t)|≤ρ，ρ>0為不確定性的上界值.

首先，選擇滑模函數(也稱切換函數)為：

(9)

式中：e(t)=r(t)-yf(t)；λ為滑模系數.

因滑模面上s(t)=0，則由式(9)可得到滑模運動方程：

(10)

基于滑模函數式(9)，針對不確定模型式(8)，可設計如下的滑模控制律：

(11)

其中，

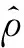
滑模控制器設計一般需要知道不確定性的上界，但這些上界值實際上難以得到.為此，使用自適應技術來對不確定性上界進行估計，式(12)為不確定性上界估計值的自適應更新律.

(12)

式中：γ為自適應增益，γ>0.

當選用式(9)所示的滑模函數，將滑模控制律式(11)作用于不確定模型式(8)時，閉環系統能夠漸進穩定.證明如下：

選擇如下的非負李亞普諾夫Lyapunov函數

(13)

對滑模函數式(9)求微分并代入控制律式(11)，可得：

(14)

(15)

2.3預估滑模控制方案的具體實施

筆者所提出的預估滑模控制方案本質上是一種利用不確定性邊界的方法，閉環系統的性能由滑模函數決定.為了減少不必要的切換，避免產生抖振現象，實際應用時可用式(16)中的飽和函數sat替換式(11)中的符號函數sign.

(16)

式中：β表示邊界層的寬度，β>0.

(17)

式中：αr為濾波系數，0<αr≤1；Ts為采樣周期；參考輸出yr(t)的初值yr(0)=y(0).

(18)

其中滑模函數

若被控對象具有參數不確定性和外部干擾，可以用下面的不確定模型表示：

(b1+Δb1)u(t-τ)+w(t)

(19)

式中：Δa1、Δa2和Δb1為系統參數不確定部分；w(t)為外部干擾.

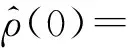
|w(0)|

(20)

預估滑模控制器包含4個參數：α、β、λ和γ.α與閉環系統的性能相關，α越大，系統的響應越快，但此時控制作用較大.引入參數β是為了消除輸入的抖振，通常β的選擇是為了權衡控制精度和輸入抖振程度.滑模函數中系數λ的取值會影響滑模運動軌跡，從而進一步影響系統的性能.自適應增益γ用于調整不確定性上界估計值的收斂速率.

2.4推廣應用于非最小相位過程

對于非最小相位系統，其階躍響應會出現負調，這對實施控制非常不利，如何在克服負調的同時抑制超調并縮短過渡時間是一個控制難題.筆者通過對辨識模型進行簡單處理，將預估滑模控制方案直接推廣應用于控制非最小相位過程.

假定對非最小相位過程進行辨識后得到如下SOPDT模型：

(21)

式中：b2/b1<0，因為非最小相位過程具有不穩定零點(即右半復平面零點).

非最小相位模型式(21)可近似轉化為標準的無零點SOPDT模型：

(22)

根據式(21)中的分子部分b2s+b1，利用指數函數的一階泰勒級數式(23)可近似得到等價遲延時間τeq≈-b2/b1.

(23)

因此，前面基于無零點SOPDT模型的預估滑模控制方法就可以直接處理非最小相位過程.雖然等價遲延時間方法會帶來額外的建模誤差，但這種增加的模型不確定性可以很容易地通過適當提高不確定性上界初始估計值和自適應技術來解決.

3CFB鍋爐床溫的預估滑模控制仿真研究

將所提出的預估滑模控制(Predictive Sliding Mode Control，PSMC)方法應用于CFB鍋爐給煤量-床溫通道的床溫控制.為便于對比，文中利用另外2種具有較強魯棒性的控制方法，即Camacho等[9]提出的基于內模的滑模控制方法(IM-SMCr)和Morari等[10]提出的基于內模思想整定的PID控制方法(IMC-PID)，也分別設計了相應的床溫控制系統.表2列出了3種不同控制系統在90%負荷下采用大同煙煤的給煤量-床溫模型作為標稱模型而設計的控制器參數取值.

表2　3種不同控制系統的控制器參數

試驗1：床溫設定值跟蹤.

假定90%負荷下床溫設定值從887 ℃階躍升高5 K，圖3所示為應用不同控制方法時床溫響應曲線和控制器輸出(即給煤變化量)曲線.從圖3可以看出，采用PSMC方法能獲得更小的超調量和更短的調節時間，控制效果明顯優于IM-SMCr方法和IMC-PID方法.在控制器參數不變的情況下，圖4給出了在80%負荷下床溫設定值從873 ℃階躍升高5 K時的控制效果，由于負荷變化后床溫模型與實際對象特性不匹配，3種控制系統的性能均有所下降，但PSMC方法的性能仍優于其他方法.

試驗2：抗階躍外擾.

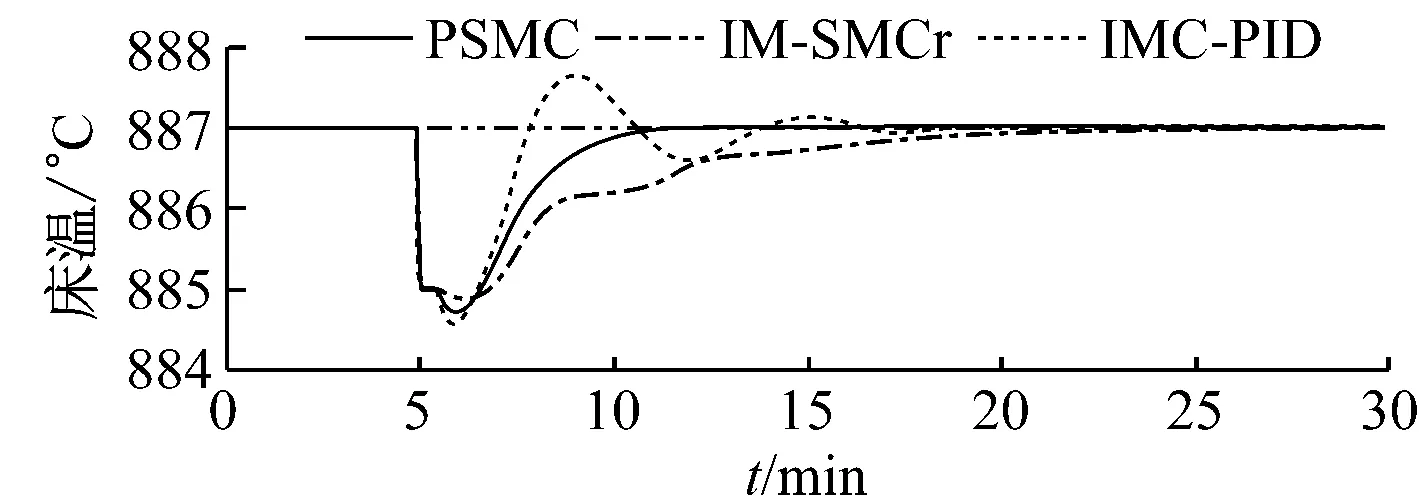
假設由于一次風、二次風配比、石灰石量、排渣量或返料量等因素的影響導致床溫在t=5 min時偏離其設定值2 K.圖5和圖6分別給出了90%和70%負荷下不同床溫控制系統的抗外擾效果.由圖5和圖6可知，在模型與對象匹配的情況下，PSMC方法具有很強的抗外擾能力，能在短時間內抑制住床溫的波動且動態偏差小；在模型與對象不匹配的情況下，雖然控制性能有所下降，但仍能進行有效控制.

試驗3：抗給煤量擾動.

(a)

(b)

(a)

(b)

(a)

(b)

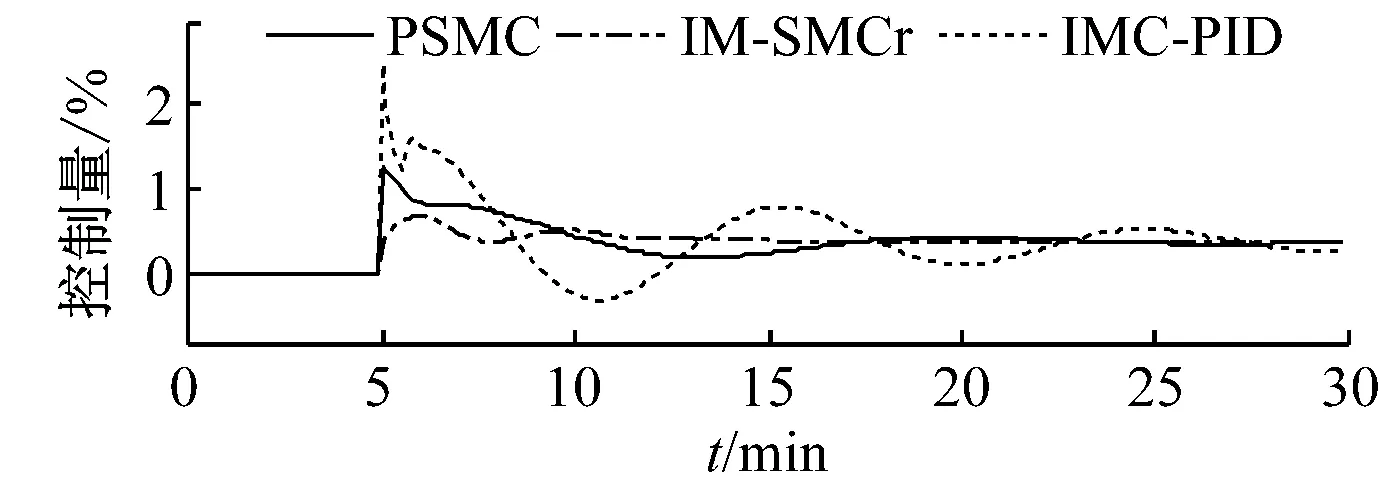
假定給煤量發生自發性擾動，在t=10 min時突然增加0.5%.圖7和圖8分別給出了90%和70%負荷下床溫控制系統的抗內擾性能.由圖7和圖8可知，在模型與對象匹配的情況下，PSMC方法具有很強的抗內擾能力，能在很短時間內抑制床溫的波動且動態偏差小；在模型與對象不匹配的情況下，雖然控制性能有所下降，但仍能進行有效控制.

試驗4：抗煤質擾動.

(a)

(b)

(a)

(b)

(a)

(b)

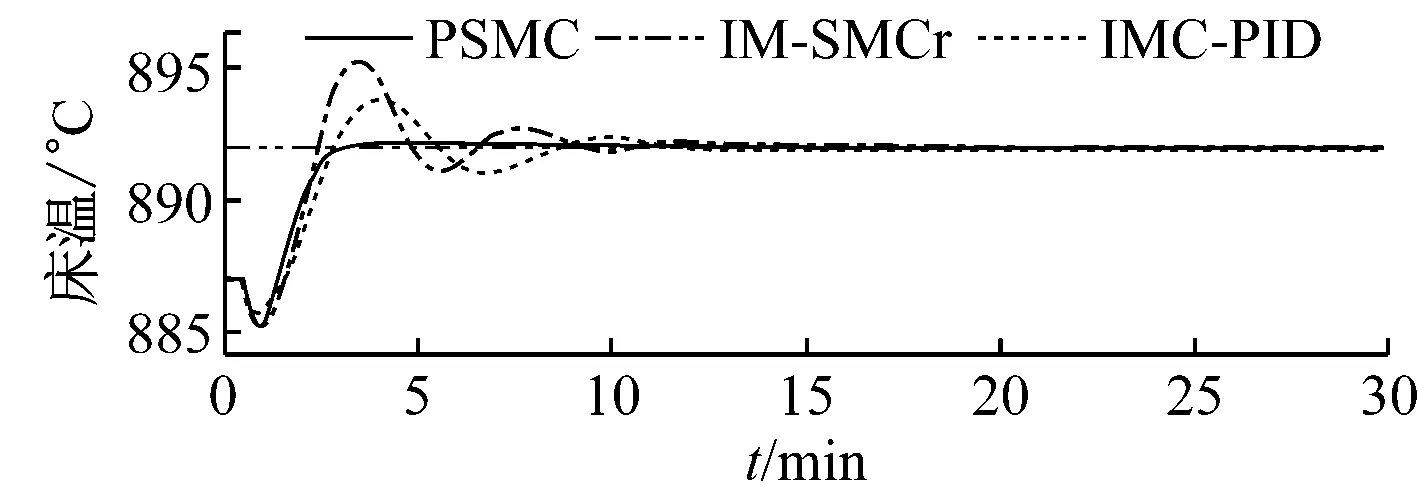
假定90%負荷下床溫穩定在其相對設定值1上，對應控制量相對值為0.268 8，在t=5 min時煤種由原來的大同煙煤變化為陽山無煙煤，煤質變化導致床溫偏離其設定值.3種控制系統的控制效果如圖9所示，在PSMC方法的控制作用下床溫能夠快速地恢復到原來的設定值.圖10給出了70%負荷下煤種發生變化時的控制效果，由于70%負荷下采用陽山無煙煤時床溫動態特性與90%負荷下采用大同煙煤時的特性差異較大，因而3種控制系統的控制效果均有所下降，但總體上PSMC方法的性能仍優于其他2種控制方法.

通過上述4個仿真實驗可以看出，筆者提出的PSMC方法具有良好的設定值跟蹤性能和抗干擾能力以及強魯棒性.

(a)

(b)

(a)

(b)

4結論

針對循環流化床鍋爐床溫等具有大慣性、大滯后的復雜熱工對象因負荷、煤種、環境條件改變以及模型簡化等帶來的不確定性問題，設計了一種簡單而新穎的基于SOPDT模型的預估滑模控制方案.它基于辨識得到的標稱SOPDT模型，構建無遲延預估模型用于過程輸出預測，并通過合理設計滑模函數和不確定上界自適應估計的滑模控制律，使得具有不確定性的閉環系統能在任何外擾下保持漸進穩定.該預估滑模控制方法還可擴展應用于具有逆反應過程的非最小相位系統.針對循環流化床鍋爐床溫對象設計了相應的預估滑模控制系統，仿真結果表明：采用PSMC方法的效果明顯優于基于內模原理設計的一般滑模控制器和PID控制器，具有良好的負荷適應性及抗各種不確定性和干擾的能力.

參考文獻：

[1]于希寧，王慧，王東風，等．模糊控制在循環流化床鍋爐床溫控制中的應用[J]．華北電力大學學報，2005，32(3)：43-46．

YU Xining, WANG Hui, WANG Dongfeng,etal. Application of fuzzy-PID control algorithm in bed temperature control of circulating fluidized bed boiler[J]. Journal of North China Electric Power University, 2005, 32(3): 43-46.

[2]馬寶萍，司鳳琪，徐治皋，等．基于遺傳算法的循環流化床鍋爐床溫模糊控制系統[J]．中國電機工程學報， 2001，21(11)：69-73．

MA Baoping, SI Fengqi, XU Zhigao,etal. Genetic-based fuzzy bed temperature control system of circulating fluidized bed boiler[J]. Proceedings of the CSEE, 2001, 21(11): 69-73.

[3]林永君，管志敏，彭鋼，等．基于自抗擾控制的循環流化床鍋爐床溫系統的研究[J]．熱能動力工程，2010，25(5)：514-516.

LIN Yongjun, GUAN Zhimin, PENG Gang,etal. Study of the bed temperature system for a circulating fluidized bed boiler based on a self disturbance-resistant control[J]. Journal of Engineering for Thermal Energy & Power, 2010, 25(5): 514-516.

[4]張媛媛．神經網絡預測控制在循環流化床鍋爐床溫系統的應用[J]．電力學報，2009，24(2)：121-124．

ZHANG Yuanyuan. NN predictive control of CFB bed temperature system[J]. Journal of Electric Power, 2009, 24(2): 121-124.

[5]董湛波，向文國，王新．基于多模型的循環流化床鍋爐床溫預測控制[J]．動力工程學報，2011，31(3)：181-186．

DONG Zhanbo, XIANG Wenguo, WANG Xin. Predictive control on bed temperature of CFB boilers based on multiple models[J]．Journal of Chinese Society of Power Engineering, 2011, 31(3): 181-186.

[6]劉金昆，孫富春．滑模變結構控制理論及其算法研究與進展[J]．控制理論與應用，2007，24(3)：407-418．

LIU Jinkun, SUN Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory & Applications, 2007, 24(3): 407-418.

[7]陳志梅，貞艷，張井崗．滑模變結構控制理論及應用[M]．北京：電子工業出版社，2012．

[8]仇韜．循環流化床鍋爐在負荷和煤質波動下的控制問題研究[D]．北京：清華大學，2007．

[9]CAMACHO O, ROJAS R, GARCíA-GABíN W. Some long time delay sliding mode control approaches[J]. ISA Transactions, 2007, 46(1): 95-101.

[10]MORARI M, ZAFIRIOU E. Robust process control[M]. New Jersey, USA:Prentice-Hall, Englewood Cliffs, 1989.

Predictive Sliding Mode Control on Bed Temperature of CFB Boilers

ZHUHongxia1,2,SHENJiong1,LIYiguo1

(1. School of Energy and Environment, Southeast University, Nanjing 210096, China; 2. School of Energy and Power Engineering, Nanjing Institute of Technology, Nanjing 211167, China)

Abstract：To tackle the uncertainties caused by variations of load, coal and environmental conditions as well as by model simplification, a predictive sliding mode control strategy, which is easily understandable and applicable in practice, was proposed for the thermal processes with large inertia or time delay. Firstly, a predictive model without output delay was established to estimate the process output by using a second-order plus dead-time (SOPDT) model obtained in nominal case. Secondly, a reasonable sliding function and a sliding mode control law with adaptively estimated uncertain upper bound were designed to asymptotically stabilize the closed-loop system with uncertainties and disturbances. On the basis above, numerical simulations were conducted on bed temperature of a circulating fluidized bed (CFB) boiler. Results show that the control strategy proposed is fast in bed temperature regulation with small overshoot and strong anti-disturbance capability.

Key words：predictive sliding mode control; SOPDT model; uncertainty; circulating fluidized bed; bed temperature

收稿日期：2015-06-29

基金項目：國家自然科學基金資助項目(51476027)； 教育部高等學校博士學科點專項科研基金資助項目(20130092110061)； 南京工程學院青年基金資助項目(QKJA201303)

作者簡介：朱紅霞(1980-)，女，江蘇南通人，副教授，博士研究生，研究方向為先進控制理論在熱工過程中的應用.

文章編號：1674-7607(2016)05-0365-07中圖分類號：P273

文獻標志碼：A學科分類號：470.20

電話(Tel．)：13512535256；E-mail：zhxia@njit.edu.cn.