反比例函數(shù)思想方法

萬(wàn)永良

?

思維訓(xùn)練營(yíng)/思想方法

反比例函數(shù)思想方法

萬(wàn)永良

數(shù)學(xué)思想方法是從數(shù)學(xué)內(nèi)容中提煉出來的數(shù)學(xué)學(xué)科的精髓，是數(shù)學(xué)素養(yǎng)的重要內(nèi)容之一.它揭示了概念、原理、規(guī)律的本質(zhì)，是溝通基礎(chǔ)與能力的橋梁.反比例函數(shù)一章中主要有數(shù)形結(jié)合思想、函數(shù)與方程思想、分類討論思想等.

一、數(shù)形結(jié)合思想

數(shù)形結(jié)合就是把數(shù)量關(guān)系與幾何圖形結(jié)合起來，通過“以形助數(shù)”或“以數(shù)解形”使復(fù)雜問題簡(jiǎn)單化，抽象問題具體化，從而優(yōu)化解題過程.

A.k1＞k2＞k3B.k3＞k2＞k1

C.k2＞k1＞k3D.k3＞k1＞k2

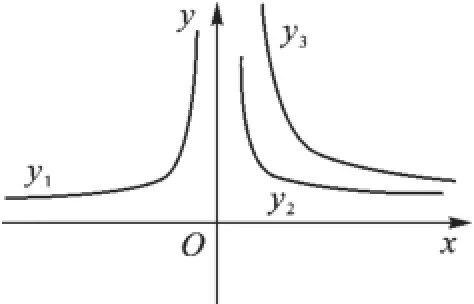
圖1

【解析】先看位置：當(dāng)k＞0時(shí)，兩支雙曲線分別位于一、三象限內(nèi)，當(dāng)k＜0時(shí)，兩支雙曲線分別位于二、四象限內(nèi)，故k1＜0，k2＞ 0，k3＞0；另一方面越小，圖像就越接近坐標(biāo)軸，故k3＞k2.綜合所述，可得k3＞k2＞k1，選B.

【點(diǎn)評(píng)】在解決反比例函數(shù)的問題時(shí)，熟練掌握反比例函數(shù)的圖像與系數(shù)k的關(guān)系，把數(shù)和形結(jié)合起來是解答這類問題的關(guān)鍵.另外，此題還可用特殊值法，也就是用一個(gè)具體數(shù)值代替這個(gè)式子中的字母求解圖像問題.

A.圖像經(jīng)過點(diǎn)（1，-2）

B.x＜0時(shí)，y隨x增大而減小

C.x＞0時(shí)，y隨x增大而增大

D.圖像與直線y=-x有兩個(gè)交點(diǎn)

【解析】選B.

【點(diǎn)評(píng)】畫出函數(shù)示意圖便能輕松獲解.

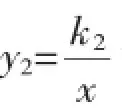
（1）求反比例函數(shù)y1、y2和一次函數(shù)y3的表達(dá)式；

（2）結(jié)合圖像，求出當(dāng)y3＞y2＞y1時(shí)的取值范圍.

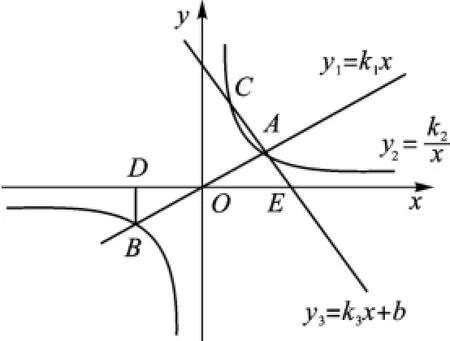
圖2

（2）x＜-4或1＜x＜4.

【點(diǎn)評(píng)】對(duì)于第一問，由k的幾何意義

圖2可得k2=8，從而得到A點(diǎn)的坐標(biāo)，進(jìn)一步求出k1，再由A、E兩點(diǎn)坐標(biāo)用待定系數(shù)法求出k3和b；對(duì)于第二問，一般不用不等式求取值范圍，而用以形助數(shù)手段直接觀察圖像得到.

二、函數(shù)與方程思想

方程思想就是根據(jù)所要解決的問題建立方程模型.

（1）當(dāng)點(diǎn)P1的橫坐標(biāo)逐漸增大時(shí)，△P1OA1的面積將如何變化？

（2）若△P1OA1與△P2A1A2均為等邊三角形，求此反比例函數(shù)的表達(dá)式及A2的坐標(biāo).

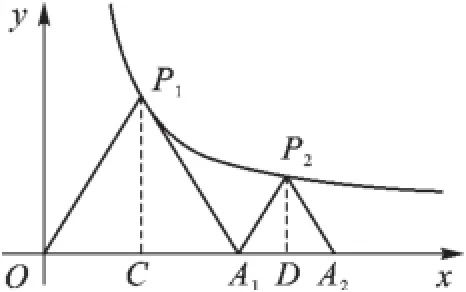
圖3

【解析】（1）△P1OA1的面積將逐漸減小；

【點(diǎn)評(píng)】把兩個(gè)正三角形換成正方形或等腰三角形，仍可列方程求解.

（1）求k的值；

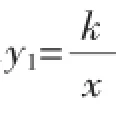
【解析】（1）k=8；

【點(diǎn)評(píng)】此題考查了用待定系數(shù)法求反比例函數(shù)表達(dá)式中k的值，同時(shí)也考查了反比例函數(shù)性質(zhì)與方程思想.

三、分類討論思想

分類討論思想就是當(dāng)我們要解決的問題不能完全確定時(shí)，按問題出現(xiàn)的各種情況進(jìn)行分類，分別作出與各分類相應(yīng)的結(jié)論.

【解析】當(dāng)兩點(diǎn)在同一象限時(shí)，即當(dāng)x1> x2>0或0＞x1>x2時(shí)，由于k>0，所以y隨x的增大而減小.因?yàn)閤1>x2，所以y1＜y2.

當(dāng)兩點(diǎn)不在同一象限時(shí)，即當(dāng)x1>0>x2時(shí)，因?yàn)閗>0，x1>0所以y1>0.同理y2＜0，所以y1>y2.

作者單位：（江蘇省常州市武進(jìn)區(qū)前黃實(shí)驗(yàn)學(xué)校）