一類具記憶項的二階線性發展方程的能量衰減估計
蘭琳琳,蒲志林
(四川師范大學數學與軟件科學學院,四川成都610066)
一類具記憶項的二階線性發展方程的能量衰減估計
蘭琳琳,蒲志林*
(四川師范大學數學與軟件科學學院,四川成都610066)
研究一類具記憶項的線性發展方程的能量衰減估計,通過Lyapunov函數的運用和函數的構造來證明當記憶核在條件α'(s)≤-β(s)α(s)下衰減時,方程的能量按照多項式方式衰減.
線性發展方程;多項式衰減;Lyapunov函數
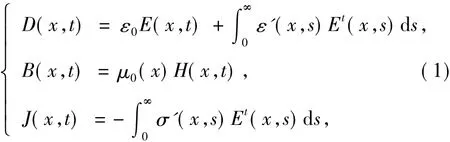
考慮一類具有記憶的導電材料的模型
其中,Et(s)=E(t-s),s≥0,B、E、H、D、J分別表示了磁感應強度、電場、磁場強度、電位移、感應電流密度,ε0是介電常數,μ0是導磁系數,ε'、σ'是記憶核.文獻[1]通過半群方法證明了方程(1)當t→∞時其能量成指數型衰減,由于方程D=ε0E無法用來計算電磁波的吸收和耗散現象,文獻[2]基于方程(1),通過重新對D和E的遺傳性關系的建立,研究了電磁波的吸收和耗散現象,文獻[3]對方程(1)的記憶項進行了推廣,研究了更一般的線性基本方程,文獻[4]證明了方程(1)中當D由E和H的線性函數共同決定時,電磁材料熱力學系統的自由焓的非唯一性成立,并且Clausius-Duhem不等式在有記憶項的系統中作為等式成立,當電磁場很弱時,文獻[5]基于方程(1)運用線性方法構造出下面的基本方程進而對電離層的現象進行了研究

文獻[6]通過將方程(1)進行一些條件限制后代入Maxwell方程中,得到方程
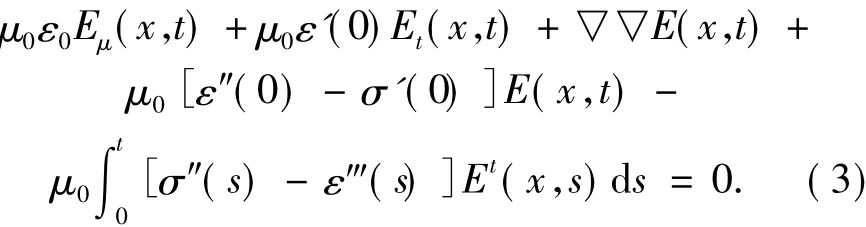
由于沒有自由電荷,即:D=0,得到:E=0(參見文獻[7]),進一步有:E=-ΔE,當ε0=μ0=1且α1=ε'(0)時,形成了嚴格電導體的模型

并對這個新的方程進行了能量衰減估計,證明當記憶核滿足條件

呈指數方式衰減時,其能量按照多項式方式衰減.本文弱化了記憶核α(s)的限制條件,使其結果推廣到更廣泛的情況,這個限制條件是 α:[0,∞)→[0,∞)是局部絕對連續函數,α(s)>0,存在β(s)>0使得下列不等式成立:α'(s) ≤-β(s)α(s),其中β滿足的條件為:β是R+→R+上的非增可微函數,α'(s)≤- β(s)α(s),s≥ 0,,此處的假設條件就包括了下面的幾種情況[8]:同時,此處的假設條件包含了指數方式衰減的條件,最終證明當記憶核在條件α'(s)≤-β(s)α(s)下衰減時,方程(4)的解按照多項式方式衰減.

1 記號與引理
令Ω?R3為一個具有Lipschitz邊界的有界區域,并且在Ω中引進L2(Ω)空間,〈·,·〉為L2空間中的內積,‖·‖為L2(Ω)空間中的范數.
對任意的α∈C(R)和E∈W1,2(0,T),定義:

引理 1.1 對任意的 α∈ C(R)和 E∈W1,2(0,T)有

證明 運用* 和◇的定義可以得證.
引理 1.2 對任意的 α∈ C1(R)和 E∈W1,2(0,T)有

證明

等式右邊為

因為

等式右邊為

等于等式左邊,得證.
引理1.3[9-10]當L(t)為Lyapunov函數,滿足

則存在常數C>0,使得

特別地,當r=0時有

2 主要結論及證明
我們規定方程(4)滿足當記憶核 α是[0,∞)→[0,∞)上的絕對連續函數且:

存在β(s)≥0使得

且有

定理2.1 當假設α∈C1(R+)∩L1(R+)且E是方程(4)的解,則能量方程可以寫作

并且有

定理2.1的證明 對方程(4)兩邊關于Et在Ω上積分


由引理1.2得:

取

因為

所以

且

定理2.2 當α滿足假設條件(20)~(24)式,則方程(4)的解由指數衰減到0,即存在一個正的常數珘C使得
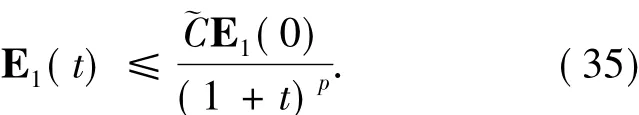
定理2.2的證明 首先定義函數

方程兩邊同時求導

由方程(4)得

代入得

由引理1.1得

對上式的最后一項進行下面的處理,則


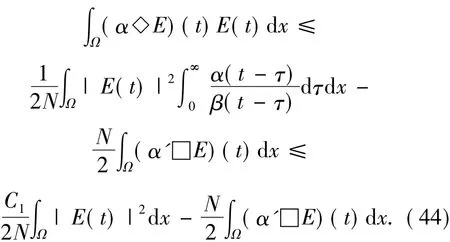
將最后一項由上面的不等式替換得

下面再定義函數

其中N待定且充分大,然后對方程兩邊同時求導

將(32)和(49)式代入

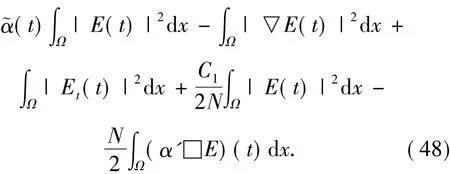
對系數進行整理得到


最后定義函數

由N(t)、E1(t)以及L(t)的表達式可知,存在c0、c1>0,使得:

令

當0≤r<1,p≥2,則有:

令

則有

c3>0,由(54)和(55)式

由(57)和(64)式得


由引理1.3有
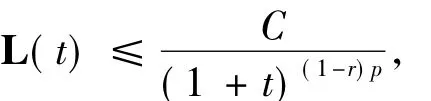
由L(t)和E1(t)的定義,可得到
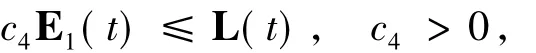
從而有


[1]MARIA GRAZIA N,ELENA V.On the exponential stability of electromagnetic systems with memory[J].Int Math J,2002,1(6):575-590.
[2]HOPKINSON J.Residual charge of the leyden jar dielectric properties of different glasses[J].Philosophical Transactions of the Royal Society of London,1877,167:599-626.
[3]TOUPIN R A,RIVLIN R S.Linear functional electromagnetic constitutive relations and plane waves in a hemihedral isotropic material[J].Archive for Rational Mechanics and Analysis,1960,6(1):188-197.
[4]FABRIZIO M,MORRO A.Dissipativity and irreversibility of electromagnetic system with memory[J].Mathematical Models and Methods in Applied Science,2000,10(2):217-246.
[5]GENTILI G.Thermodynamic potentials for electromagnetic fields in the ionosphere[J].Int J Eng Sci,1995,33(11): 1561-1575.
[6]RIVERA J E M,NASO M G,VUK E.Asymptotic behaviour of the energy for electromagnetic systems with memory[J].Math Meth Appl Sci,2004,27:819-841.
[7]BLOOM F.Ill-posed Problems for Integrodifferential Equations in Mechanics and Electromagnetic Theory[M].2nd.Philadelphia:Society for Industrial and Applied Mathematics,1981.
[8]RIVERA J E M,ANDRADE D.Exponential decay of non-linear wave equation with a viscoelastic boundary condition[J].Mathematical Methods in the Applied Sciences,2000,23(1):41-61.
[9]MOHAMMAD K.Uniform decay of solutions to Cauchy viscoelastic problems with density[J].Electron J Diff Eqns,2011,2011(93):1341-1353.
[10]TEMAN R.Infinite-Demensional Dynamical Systems in Mechanics and Physics[M].New York:Springer-Verlag,1997:167-168.
The Energy Decay Estimates of a Second-order Linear Evolution Equation with Memory
LAN Linlin,PU Zhilin
(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
The paper aims to study the energy decay of a linear evolution equation with memory.We prove that the energy of the equation will decay according to the polynomial approach when the memory decays under the condition of α'(s)≤-β(s)α(s)by employing Lyapunov functional and the structure of the function.
linear evolution equation;polynomial rate of decay;Lyapunov function
O175
A
1001-8395(2016)04-0491-05
10.3969/j.issn.1001-8395.2016.04.005
(編輯 余 毅)
2015-04-10
四川省應用基礎研究項目(2015JY0125)
*通信作者簡介:蒲志林(1963—),男,教授,主要從事無窮維動力系統理論的研究,E-mail:Puzhilin908@sina.com
2010 MSC:47D06

