型A半群的Vagner-Preston表示
郭 茜,喻秉鈞
(1.成都師范學院數學學院,四川成都610041; 2.四川師范大學數學與軟件科學學院,四川成都610066; 3.成都文理學院數學教研室,四川成都610101)
型A半群的Vagner-Preston表示
郭 茜1,喻秉鈞2,3
(1.成都師范學院數學學院,四川成都610041; 2.四川師范大學數學與軟件科學學院,四川成都610066; 3.成都文理學院數學教研室,四川成都610101)
逆半群的著名的Vagner-Preston表示定理是群的經典Cayley表示定理向逆半群的一個推廣.將這個結果進一步推廣到了型A半群上,給出了型A半群的Vagner-Preston表示定理,證明了任一型A半群都是某對稱逆半群的型A子半群,此結論也體現了型A半群在富足半群中的地位正恰如逆半群在正則半群中的地位.通過2個例子說明,既存在不是型A半群的恰當半群S,使?是S的一個表示;也存在不是型A半群的恰當半群S,使?不是一個表示.于是就富足半群類而言,該表示不能推廣.
恰當半群;型A半群;同態;Vagner-Preston表示
1 預備知識
俄國數學家V.V.Vagner[1]和英國數學家G.B.Preston[2]分別于1952和1954年獨立發現,任一非空集X上的1-1部分變換(即X中2個子集合之間的雙射)之全體所成集合I(X)在部分變換的乘積運算下成為一個逆半群,稱為對稱逆半群.他們還證明了以下關于逆半群的著名的 Vagner-Preston表示定理,簡稱為V-P表示.
Vagner-Preston表示定理[3]任一逆半群S都是某對稱逆半群的逆子半群.更準確地說,對任意a∈S定義?a滿足:,且對任意x∈Saa-1有,則,而是從S到I(S)的單同態.
它恰是關于群的Cayley表示定理(任一群G都是某集合上對稱群Sym G的子群)向逆半群的推廣.本文將這個結論進一步推廣到型A半群上,自Green*等價關系的引入,富足半群、恰當半群和型A半群等典型的廣義正則半群,成為了國內外半群學者研究的熱點[4-6].尤其是其中的型A半群,盡管它們一般不正則,但由于冪等元集構成半格,且具有類似于正則半群中冪等元的連通性,使其成為推廣逆半群研究中豐碩成果的最好對象[7-10].本文中一般定義及記號均參見文獻[11-14].
設S為半群.下述二元關系稱為S上的Green*-關系:
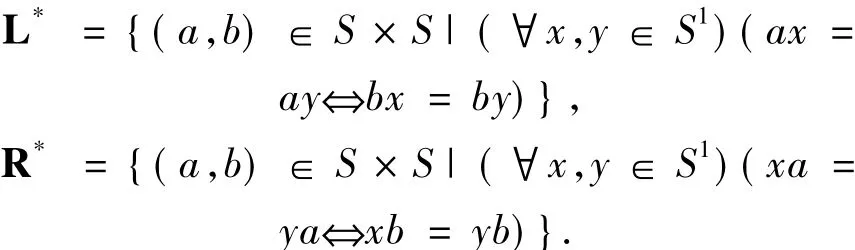
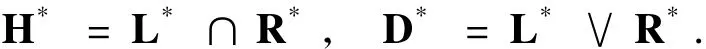
在正則半群中,有K*=K,(K=L,R,H,D).
若半群S的每個L*-和R*-類都含有冪等元,則稱S為富足半群.若富足半群S的冪等元集E(S)是半格(交換冪等元子半群),則稱S是恰當半群.恰當半群S中每個L*-、R*-類恰含一個冪等元,約定把元素a∈S所在的L*-、R*-類中那個惟一的冪等元分別用a*、a+表示有
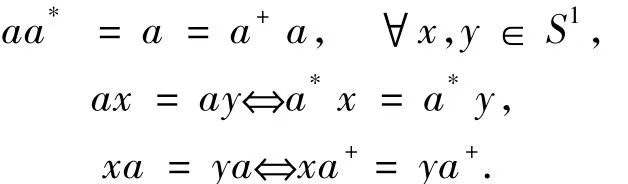
命題1.1[13]設S是恰當半群,冪等元集E是半格,那么a,b∈S有:
2)(ab)*=(a*b)*,(ab)+=(ab+)+;
3)(ab)*≤b*,(ab)+≤a+.這里≤是E上通常意義下的偏序關系.
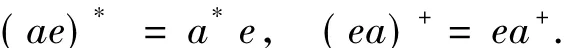
所謂型A半群是一類特殊的恰當半群,定義如下:
定義1.2[14]恰當半群S稱為型A半群,若有

2 型A半群的V-P表示
在文獻[15]中用非空集X上的所有部分變換(即從X的某子集到另一子集的滿射)所成對稱弱逆半群PJ(X)代替I(X),對型A半群證明了類似的表示定理:
定理2.1[15]設S是型-A半群,記X=S作為集合,則存在S到PJ(X)的單同態映射.
發現這個表示,事實上是型A半群S嵌入對稱逆半群I(S)的表示,即有:
定理2.2 任一型A半群S都是某對稱逆半群的型A子半群.更準確地說,對任意a∈S定義滿足:,且對任意x∈Sa+有,則,而是從S到I(S)的單同態.對任意a∈S,(S的像集合)的充要條件是a∈Reg S(S的所有正則元之集);因而特別地,當S是逆半群時,恰為V-P表示.
顯然,?是集合S上的一個部分映射.證明對任意a∈S有?a∈I(S).事實上,對任意
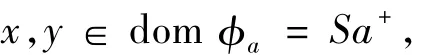
有s,t∈S使
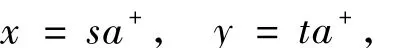
若有
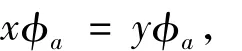
即
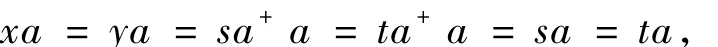
由aR*a+,有sa+=ta+,即x=y.
為證明?單,設?a=?b,a,b∈S,那么
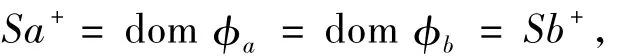
由E(S)是半格立得a+=b+.于是有
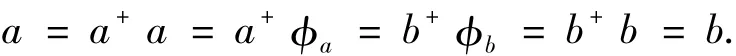
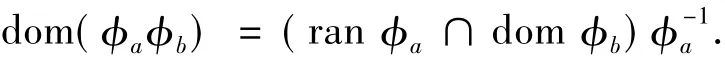
由于R*是左同余和每個R*-類只有一個冪等元,有下述推理

于是,由R*的性質和S是型A的,又有如下推理
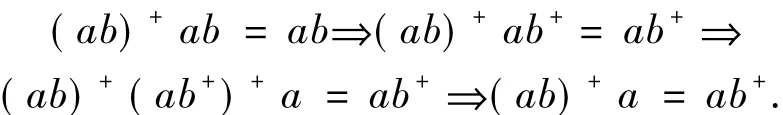
另一方面,由a+a=a有a+ab=ab,故

這說明
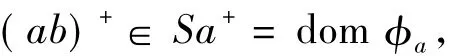
從而
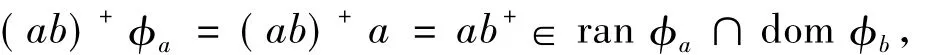
即
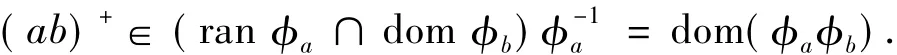
由此立得
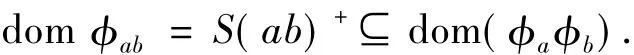
反之,對任意
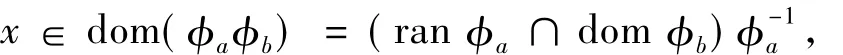
有t,u∈S使得
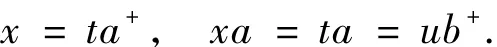
由aa*=a和E(S)是半格有
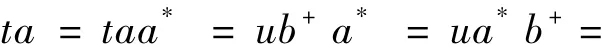
(E(S)是半格)
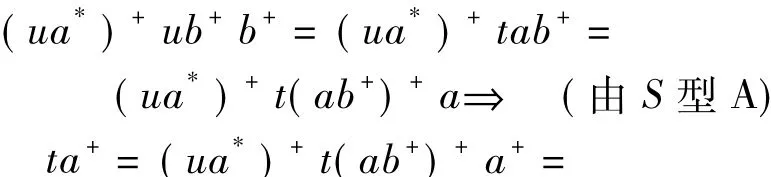
(由aR*a+)
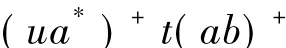
(由(ab+)+=(ab)+=(ab)+a+).
因而
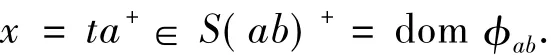
故

顯然,2個有相同定義域的部分變換只要對其定義域中每個元素的作用也相同,則兩者必相等.而
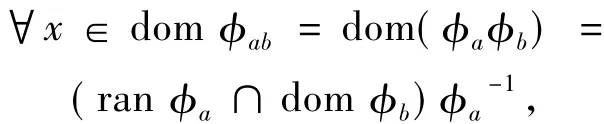
注意到此時有

有
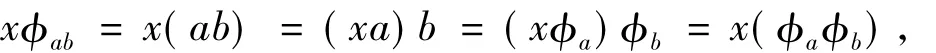
因而得到?ab=?a?b.這就證明了?是同態,從而是S的一個忠實表示.
進而,每個?a是從Sa+到Sa上的雙射.事實上,對任意xa∈Sa,x∈S,由于a+a=a有
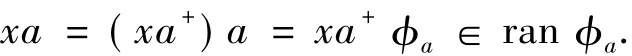

由?是單同態,立得aa'=a+.從而
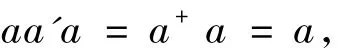
故a∈Reg S.反之,若a∈Reg S,則由Reg S是一個逆半群,有a-1∈S使得aa-1=a+,且(a-1)+= a*La,故得
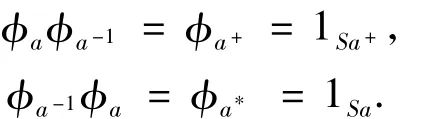
這就得到
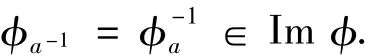
注2.3 以上定理的證明說明,若a是型A半群S的非正則元,盡管也是雙射(因而是I(S)的正則元),但它不是的正則元.
例2.5 設N是自然數集,I=N×N.在S= N∪I上定義運算·如下:
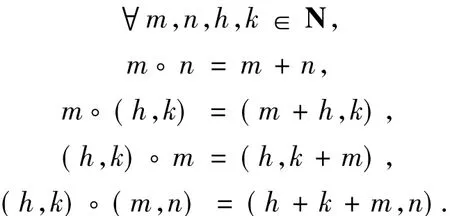
可以驗證S是一個半群.E(S)={0,(0,0)},R*-類為N和I,記J={(m,0):m∈N},則L*-類為J和SJ.可以看出,每個L*-類和每個R*-類都分別含冪等元0和(0,0);且冪等元集E(S)是二元半格.因此S是一個恰當半群.但是對任一非0正整數m有
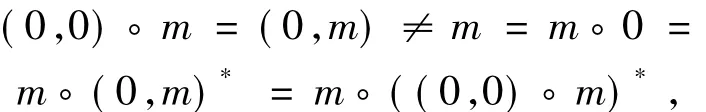
因而S不是型A半群.
該半群“蛋盒圖”如下:
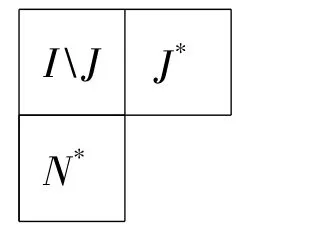
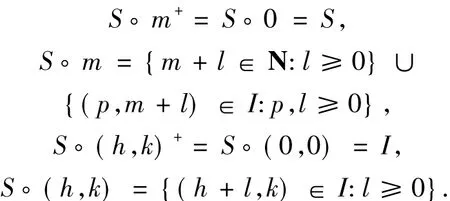
可以驗證?是S的一個表示.
例2.6 設A是生成元為a的無限單演半群,B是生成元為b的無限單演幺半群,其單位元為e.令
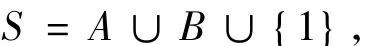
定義S上的乘法使1是S上單位元,這個乘法在A和B上的限制就是A和B自身的乘法,而A中元素與B中元素的乘法由下式定義:
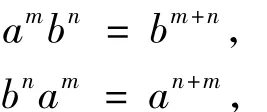
其中,m >0,n≥0,b0=e.
可以驗證S是一個半群.
E(S)={1,e},L*-類為A∪{1}和B,R*-類為A∪B和{1},H*-類為{1}、A、B.可以看出每個L*-類和每個R*-類含冪等元,且冪等元交換,因此S是一個恰當半群,其D*-類的“蛋盒圖”如下:
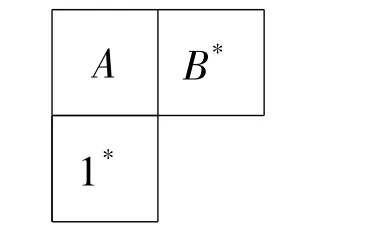
因為b=ab0=ae≠(ae)+a=b+a= ea=b0a=a.
所以S不是型A半群.

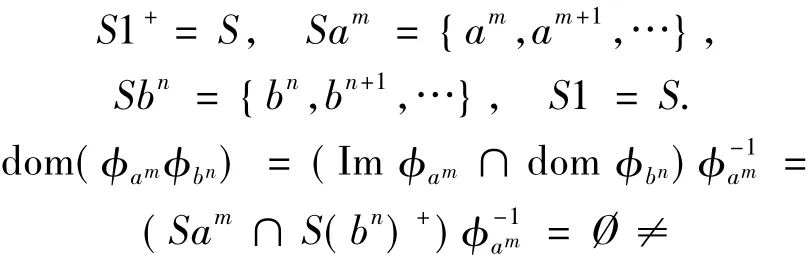
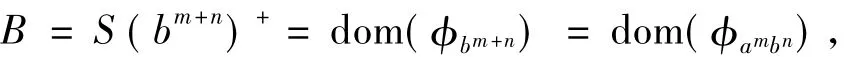
因此
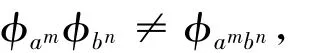
即?不是一個表示.
[1]VAGNER V V.Generalized groups[J].Doklady Akademii Nauk SSSR,1952,84:1119-1122.
[2]PRESTON G B.Inverse semi-groups[J].J London Mathematical Society,1954,29:396-403.
[3]HOWIE J M.Fundamentals of Semigroup Theory[M].London:Calrendox Press,1995:186-186.
[4]MEDGHALCHI A R,POURMAHMOOD-AGHABABA H.Figa-Talamanca-Herz algebras for restricted inverse semigroups and Clifford semigroups[J].J Math Anal Appl,2012,395(2):473-485.
[5]孫燕,任學明,宮春梅.具有左中心冪等元的U-富足半群[J].數學雜志,2015,35(4):833-840.
[6]王春茹,喻秉鈞.強右C-wlpp半群[J].四川師范大學學報(自然科學版),2015,38(2):164-168.
[7]商宇,汪立民.型A ω2-半群[J].數學進展,2015,44(4):519-529.
[8]李勇華,樂文.* -雙單型A半群[J].數學進展,2014,43(3):341-354.
[9]郭茜,喻秉鈞.型A半群在其*-閉子半群的右ω-陪集上的表示[J].四川師范大學學報(自然科學版),2009,32(2): 176-178.
[10]SHANG Y,WANG L M.The isomorphism theorem of* -bisimple type A ω2-semigroups[J].J Math Res Appl,2013,33(2):231-240.
[11]PASTIJN F.A representation of a semigroup by a semigroup of matrices over a group with zero[J].Semigroup Forum,1975,10: 238-249.
[12]FOUNTAIN J B.Aundant semigroups[J].Proc London Math Soc,1982,44:103-129.
[13]FOUNTAIN J B.Adequate semigroups[J].Proc Edinburgh Math Soc,1979,22:113-125.
[14]LAWSON M V.The structure of type-A semigroups[J].Quart J Math Oxford,1986,37(2):279-298.
[15]盧占化,馮秀峰.Type-A半群的表示[J].河南師范大學學報(自然科學版),2007,35(1):40-41.
The Vagner-Preston Representation of a Type-A Semigroup
GUO Qian1,YU Bingjun2,3
(1.College of Mathematics,Chengdu Normal College,Chengdu 610041,Sichuan; 2.College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan; 3.Office of Mathematics and Researching,Chengdu College of Arts and Sciences,Chengdu 610101,Sichuan)
The famous Vagner-Preston representation theorem of inverse semigroups is a generalization of the classical Cayley representation of groups to inverse semigroups.In this paper we generalize further it to type-A semigroups and give the Vagner-Preston representation of type-A semigroups.We prove that any type-A semigroup is a type-A sub-semigroup of the symmetric inverse semigroup.This conclusion also reflects the fact that type-A semigroup in abundant semigroups is as inverse semigroups in regular semigroups.And then,we also give examples to show that,there exist adequate semigroups which are not type-A semigroups,make the mapping a representations;and there also exist adequate semigroups which are not type-A semigroups,do not make the mapping representation.So in the class of abundant semigroups it can not be generalized any more.
adequate semigroup;type-A semigroup;homomorphism;the Vagner-Preston representation
O152.7
A
1001-8395(2016)04-0518-04
10.3969/j.issn.1001-8395.2016.04.010
(編輯 余 毅)
2015-04-21
國家自然科學基金(11371205)
郭 茜(1982—),女,講師,主要從事半群代數理論的研究,E-mail:634672198@qq.com
2010 MSC:20M30

