時標上一類p－Laplacian哈密頓系統周期解的存在性

薛益民，蘇 瑩

(徐州工程學院數學與物理科學學院，江蘇徐州221111)

時標上一類p－Laplacian哈密頓系統周期解的存在性

薛益民，蘇 瑩

(徐州工程學院數學與物理科學學院，江蘇徐州221111)

研究形式如下的時標T上非自治的p－Laplacian哈密頓系統的周期邊值問題，運用鞍點定理，得到該哈密頓系統周期解的存在性定理．作為主要結論的應用，給出了一個例子驗證所得結果．

時標;p－Laplacian哈密頓系統;周期解;鞍點定理

注［1－5］．受文獻［4－6］的啟發，本文主要研究了形

式如下的時標T上非自治的p－Laplacian哈密頓

系統周期邊值問題

其中

且滿足如下假設．

(H0)對任意的x∈Rn，F(t，x)關于t可測，對于△－a．e．t∈［0，T］T，F(t，x)關于x連續可微，且對x∈Rn和△－a．e．t∈［0，T］T，存在a∈C(R+，R+)，b∈L1(［0，T］T，R+)滿足

運用鞍點定理［7］，得到了至少一個周期解的存在性定理，推廣了文獻［6］的相關結果．作為主要結論的應用，給出了一個例子驗證了所得結果．

1 相關定義和引理

為了研究問題的需要，下面給出時標上的一些相關的基本定義，更詳盡的內容可參考文獻［6，8－16］．

定義1 設f(t)=(f1(t)，f2(t)，…，fN(t)):T→RN，t∈T，若

存在，則稱f△(t)為f在t點的△－(或Hilger)導數．若對于所有的t∈T，f△(t)存在，則稱f在T上△－(或Hilger)可微，稱f△(t):Tk→RN為f在Tk上△－導數．

定義2 若f△在Tk2=(Tk)k上可微，且f△2=(f△)△:Tk→RN，

則函數f(t):T→RN的二階導數記為f△2．

定義3 若函數f:T→RN在T每個右稠點連續，且在T左稠點極限(有限)存在，則稱f是rd－連續的．

定義4 假設f(t)=(f1(t)，f2(t)，…，fN(t)): T→RN，A是一△－可測的T的子集，則f在A上可積當且僅當fi(i=1，2，…，N)在A上可積，且

定義 5 對函數 f(t)=(f1(t)，f2(t)，…，fN(t)):［a，b］T→RN，若對，存在δ＞0，使得當是［a，b］T上任意一族互不相交的子區間，且其總長時，恒有

成立，則稱f在［a，b］T上絕對連續或全連續．

絕對連續函數有如下性質［6］:若f，g:［a，b］T→RN為絕對連續函數，則fg在［a，b］T上絕對連續，且有下式成立

設p∈R，p≥1，對空間

賦以范數

其中(．，．)表示 RN上的內積，

定義6 假設p≥1(p∈R)，u:［0，T］T→RN，則當且僅當對T)T，RN)，存在g:［0，T］T→RN使得T)T，RN)，且對，有

其中

為了更加簡潔的證明本文主要結論，下面將介紹一些用于證明p－Laplacian哈密頓系統(1)周期解存在性的相關引理．

引理1［6］如果序列{uk}k∈N在

上弱收斂于u，則{uk}k∈N在

上強收斂于u．

引理5［7］(鞍點定理) 設，其中E是實Banach空間，V≠{0}且為有限維的．假設φ∈C1(E，R)滿足P．S．條件以及

(I1)存在一個常數α和在V中0點的有界鄰域D使得

(I2)存在一個常數β＞α使得φ|X≥β，則φ有一臨界值c*≥β，且c*可表示為

其中，Γ={h∈C(珚D，E)|h=id在D上}．

2 主要結論

運用鞍點定理［7］，得到了至少一個周期解的存在性定理．

定理1 如果滿足(H0)和下面2個條件:

(H1)設，使得

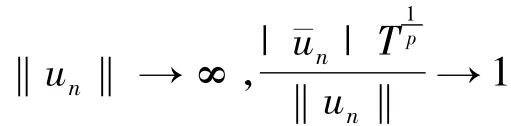
成立;

一致成立，其中

為了證明定理1，下面介紹一個引理．

引理6 設F滿足條件(H0)，且序列

滿足φ'(un)→0和{un}在上有界，則{un}在上有收斂子列．

引理6的證明 由引理2知的嵌入是緊的，因此存在一個子序列(仍記為{un})，假設存在一個點，使得在和上均有un→u0，則由引理1，在［0，T］T上un一致收斂于u0，因此

由引理4和條件(H0)有

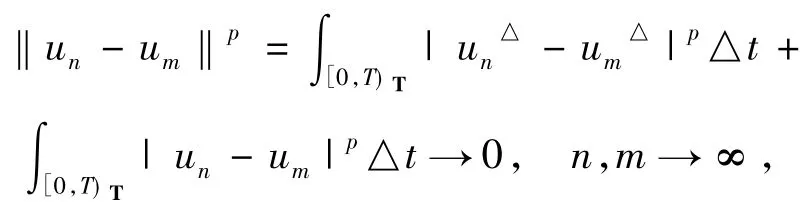
這意味著{un}在上是一個Cauchy列．根據的完備性，可得{un}是Rn)上的收斂子列．

定理1的證明 由φ的定義(3)，證明φ滿足引理5的所有條件．

且存在一個常數c，使得

則{un}在上有界．

反設結論不成立，則存在一個子序列(仍記為{un})是無界的，即

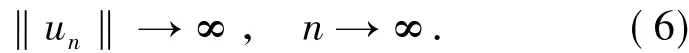
令vn=un/‖un‖，則{vn}在上有界．由引理2知的嵌入是緊的．因此，存在一個點和一個子序列(仍記為{vn})，使得在中，序列{vn}弱收斂于v0，在強收斂于v0．且存在一個函數，使得| vn|≤ω對于△－a．e．t∈［0，T］T．

由(H2)，存在常數0＜ε0＜1/pCp和M＞0，使得對u∈Rn，|u|＞M和△－a．e．t∈［0，T］T，有

成立．此外設

由(H0)，對和△－a．e．t∈［0，T］T，有

由此推斷，對u∈Rn和△－a．e．t∈［0，T］T有

由(5)和(7)式有

另一方面，根據范數的下半連續性，可得

即

由(8)和(9)式有

由引理4和時標上的控制收斂定理有

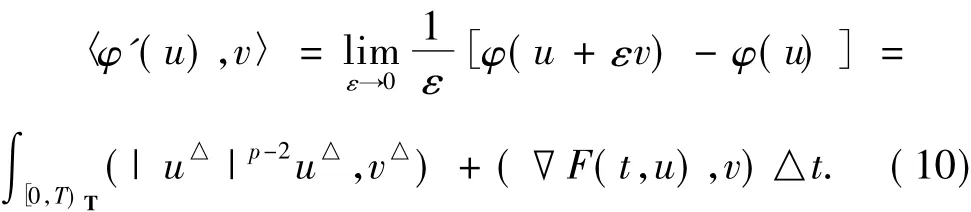
由(5)和(10)式有

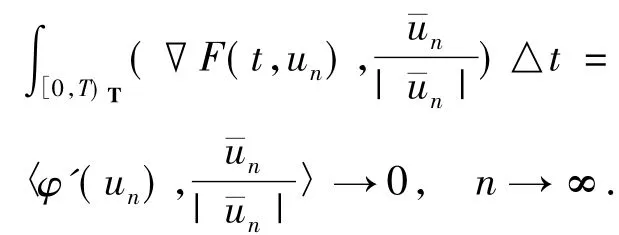
這推出了矛盾，所以假設不成立，即{un}在上有界．根據引理6，{un}在Rn)上有收斂子列，從而φ滿足P．S．條件．

則有

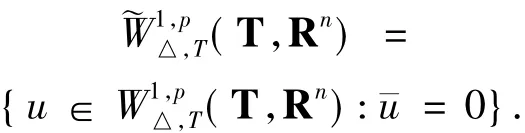
從而

下面將證明φ在Rn上是逆強制的，即

這意味著引理5的條件(I1)被滿足了．

為了得到式子(11)式，需要證明存在δ1＞0，ρ1＞0，使得對x∈Rn且|x|≥ρ1有

假設(11)不成立，則存在序列{xn}?Rn且|xn|→∞，使得下面的不等式成立

這與(H1)矛盾，由于，所以不等式(12)成立．

由(H0)可得

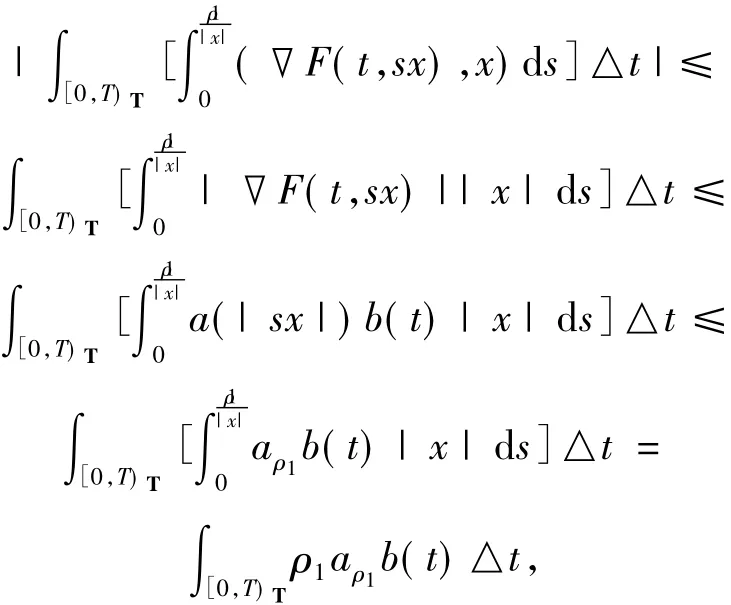
對任意的x∈Rn且|x|＞ρ1有

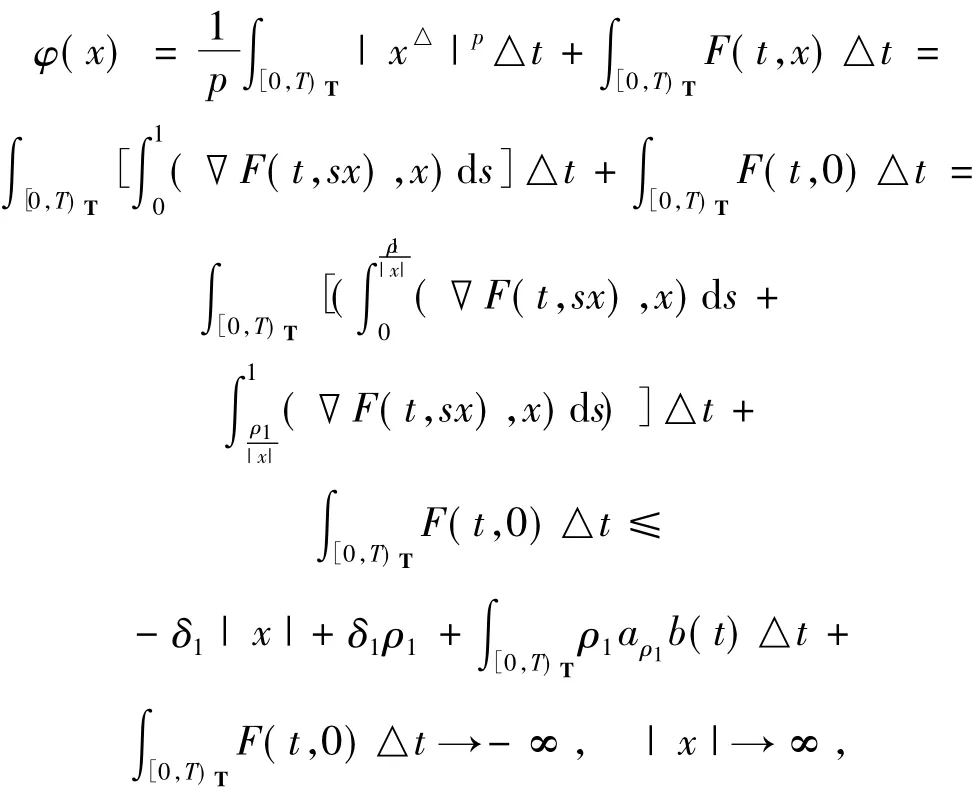
所以φ在Rn上是逆強制的．

這意味著引理5的(I2)成立．

由Cp的定義(4)有

至此，證明了φ滿足引理5的所有條件．所以根據引理5，時標上二階非自治的p－Laplacian哈密頓系統(1)在上至少存在一個解．定理證畢．

3 定理應用舉例

作為主要結論的應用，給出一個例子驗證了所得結果．

例1 設時標

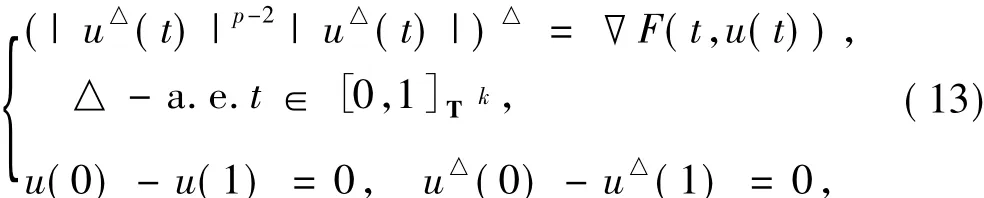
其中n∈N．考慮下面的時標T上的二階p－Laplacian哈密頓系統

其中F(t，u(t))=－λ|u|p－1(0＜λ＜1/pCp)．容易驗證其滿足(H0)和定理1的條件．由定理1推出(13)式至少存在一個解．不過函數F并不滿足文獻［6］當p=2時定理3．4的條件(ii)和定理3．6的條件(iv)．所以，從某種程度上說定理1推廣了文獻［6］的相關研究結果．

致謝 徐州工程學院重點項目(2013102)、徐州工程學院青年項目(XKY2013314)對本文給予了資助，謹致謝意．

［1］SU Y H．Multiple positive pseudo－symmetric solutions of p－Laplacian dynamic equations on time scales［J］．Math Comput Mod，2009，49(7/8):1664－1681．

［2］SU Y H．Existence theory for positive solutions of p－Laplacian multi－point BVPs on time scales［J］．Turk J Math，2011，35(2):219－248．

［3］SU Y H．Arbitrary positive solutions to a multi－point p－Laplacian boundary value problem involving the derivative on time scales［J］．Math Comput Mod，2011，53(9/10):1742－1747．

［4］SU Y H，LI W T．Periodic solutions for non－autonomous second order Hamiltonian systems on time scales［J］．Dynam SystemsAppl，2009，18:621－636．

［5］SU Y H，LI W T．Periodic solutions of second order Hamiltonian systems with a change sign potential on time scales［J］．Discrete Dyn Nat Soc，2009，2009:1－17．

［6］ZHOU J，LI Y．Sobolev’s spaces on time scales and its applications to a class of second order Hamiltonian systems on time scales［J］．Nonlinear Anal，2010，73(5):1375－1388．

［7］RABINOWITZ P H．Minimax Method in Critical Point Theory with Applications to Differential Equations［C］//BMS Regional Conference Series in Mathematics．Providence:Am Math Soc，1986，65:25－29．

［8］LAKSHMIKANTHAM V，Sivasundaram S，Kaymakcalan B．Dynamic Systems on Measure Chains［M］．Boston:Kluwer Academic Publishers，1996．

［9］GUSEINOV G．Integration on time scales［J］．J Math Anal Appl，2003，285(1):107－127．

［10］CABADA A，VIVERO D R．Criterions for absolutely continuity on time scales［J］．J Difference Eqns Appl，2005，11(1): 1013－1028．

［11］AGARWAL R P，ESPINAR V O，PERERA K，et al．Basic properties of Sobolev’s spaces on bounded time scales［J］．Adv Diff Eqns，2006，2006:1－14．

［12］RYNNE B P．Lpspaces and boundary value problems on time－scales［J］．J Math Anal Appl，2007，328(2):1217－1236．

［13］DAVIDSON F A，RYNNE B P．Eigenfunction expansions in Lpspaces for boundary value problems on time－scales［J］．J Math Anal Appl，2007，335(2):1038－1051．

［14］SUN H R，LI W T．Existence theory for positive solutions to one－dimensional p－Laplacian boundary value problems on time scales［J］．Diff Eqns，2007，240(2):217－248．

［15］袁曉紅，周德高，許方，等．非線性項帶導數的p－Laplacian邊值問題解的存在性［J］．徐州工程學院學報(自然科學版)，2010，25(1):1－5．

［16］董寧青，安天慶，艾孜瑪洪．努爾別克．二階非自治(q，p)－Laplacian方程周期解的存在性［J］．四川師范大學學報(自然科學版)，2012，35(5):605－609．

Existence of Periodic Solutions for p-Laplacian Hamiltonian System on Time Scales

XUE Yimin，SU Ying

(School of Mathematics and Physics，Xuzhou Institute of Technology，Xuzhou 221116，Jiangsu)

In this paper，we study a non-autonomous p-Laplacian Hamiltonian system on time scales T of the formThe existence of periodic solutions is proved for this Hamiltonian system by means of the saddle point theorem．As an application，a example is given to illustrate the main results．

time scales;p-Laplacian Hamiltonian system;periodic solutions;saddle point theorem

O175

A

1001－8395(2016)04－0522－06

10．3969/j．issn．1001－8395．2016．04．011時標上的動力方程越來越受到學者們的關

(編輯 陶志寧)

2015－11－03

國家自然科學基金(11501560、11301454)、國家自然科學數學天元基金(11526177)、江蘇省自然科學基金(BK20151160)、江蘇省高校自然科學基金(14KJB110025)和江蘇省六大人才高峰項目(2013－JY－003)

薛益民(1977—)，男，講師，主要從事微分方程及其應用研究，E－mail:xueym@xzit．edu．cn

2010 MSC:34B15;39A10