加權(quán)期望殘差極小化方法求解一類隨機混合變分不等式

沙明娥

(昆明學(xué)院數(shù)學(xué)系，云南昆明650214)

加權(quán)期望殘差極小化方法求解一類隨機混合變分不等式

沙明娥

(昆明學(xué)院數(shù)學(xué)系，云南昆明650214)

考慮有限維空間中的一類隨機混合變分不等式，將求解隨機混合變分不等式轉(zhuǎn)化為加權(quán)期望殘差極小化模型，并在一定條件下，通過擬蒙特卡洛方法得到了加權(quán)期望殘差極小化模型的解．

隨機混合變分不等式;加權(quán)期望殘差極小化模型;擬蒙特卡洛方法

1 預(yù)備知識

有限維空間中的混合變分不等式被廣泛應(yīng)用于實際問題之中．經(jīng)濟數(shù)學(xué)中的某些均衡問題、物理中的彈性力學(xué)問題等都可以在一定條件下轉(zhuǎn)化為混合變分不等式加以研究．就實際問題而言，系統(tǒng)往往會受到隨機因素的干擾，為了更好的描述實際問題，有必要研究隨機混合變分不等式．假定(Ω，F(xiàn)，P)是一概率空間，F(xiàn):Rn×Ω→Rn和f:Rn× Ω→R是兩函數(shù)，K∈Rn是一非空閉凸集．隨機混合變分不等式可以表述為:找x∈K滿足

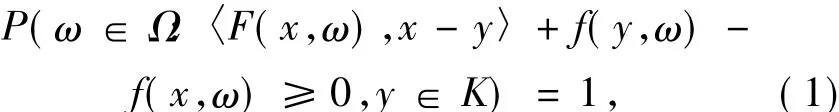
或等價表示為

其中a．s．表示在概率P下幾乎必然成立．

近年來，許多研究者研究了類似的問題，例如，X．J．Chen等［1］研究了隨機線性相補問題，并用期望殘差極小化方法求解了隨機線性相補問題;C．Zhang等［2］用期望殘差極小化方法求解了隨機非線性相補問題;M．J．Luo等［3］將期望殘余極小化方法運用于隨機變分不等式，并用該方法求解了隨機變分不等式問題;H．Q．Ma等［4］研究了隨機擬變分不等式問題，并用期望殘差極小化方法求解了該問題，其他研究工作可參見文獻［5－12］．

另一方面，由于期望殘差極小化模型具有解不穩(wěn)定，可能會出現(xiàn)多解情況等缺點，F(xiàn)．Liu等［13］改進了期望殘差極小化方法，采用加權(quán)期望殘余法求解了隨機變分不等式問題．受以上工作啟發(fā)，本文用加權(quán)期望殘余法求解隨機混合變分不等式問題，并用擬蒙特卡洛方法給出了該問題的解．

假定(Ω，F(xiàn)，P)是一概率空間，記E(·)為在概率P下的期望，‖·‖表示Rn空間的歐幾里得范數(shù)，F(xiàn):Rn×Ω→Rn和f:Rn×Ω→R是兩函數(shù)，K∈Rn是一非空閉凸集．

首先給出本文將用到的一些假設(shè)和引理．

(A)對于x∈K，

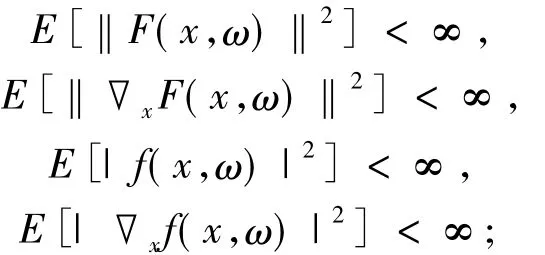
(B)對于ω∈Ω;x，y∈K，

(C)對于ω∈Ω;x，y∈K，

(D)對于ω∈Ω;x，y∈K，

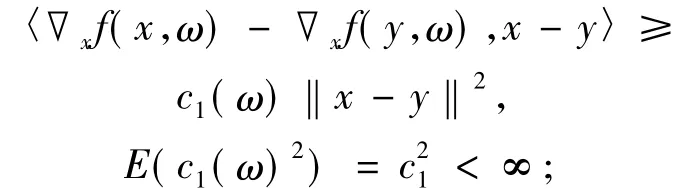
(E)對于ω∈Ω;x，y∈K，

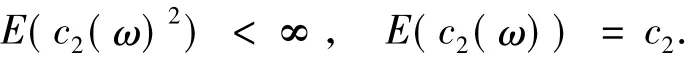
引理1．1［14］如果在Ω上可積，那么

引理1．2［12］若函數(shù) F1:Rn×ω→Rn1×n1，F(xiàn)2: Rn×ω→Rn1，xk∈Rn．當(dāng)k→∞時xk→x*．假設(shè)對于，以下式子成立

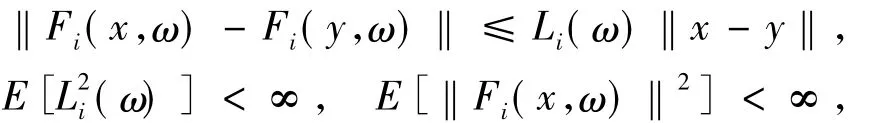
那么以下結(jié)論成立:

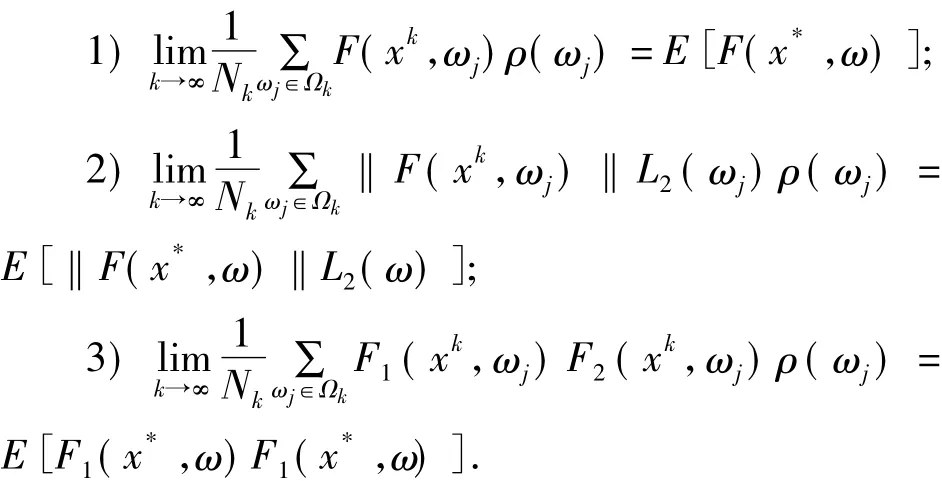
定義

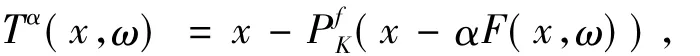
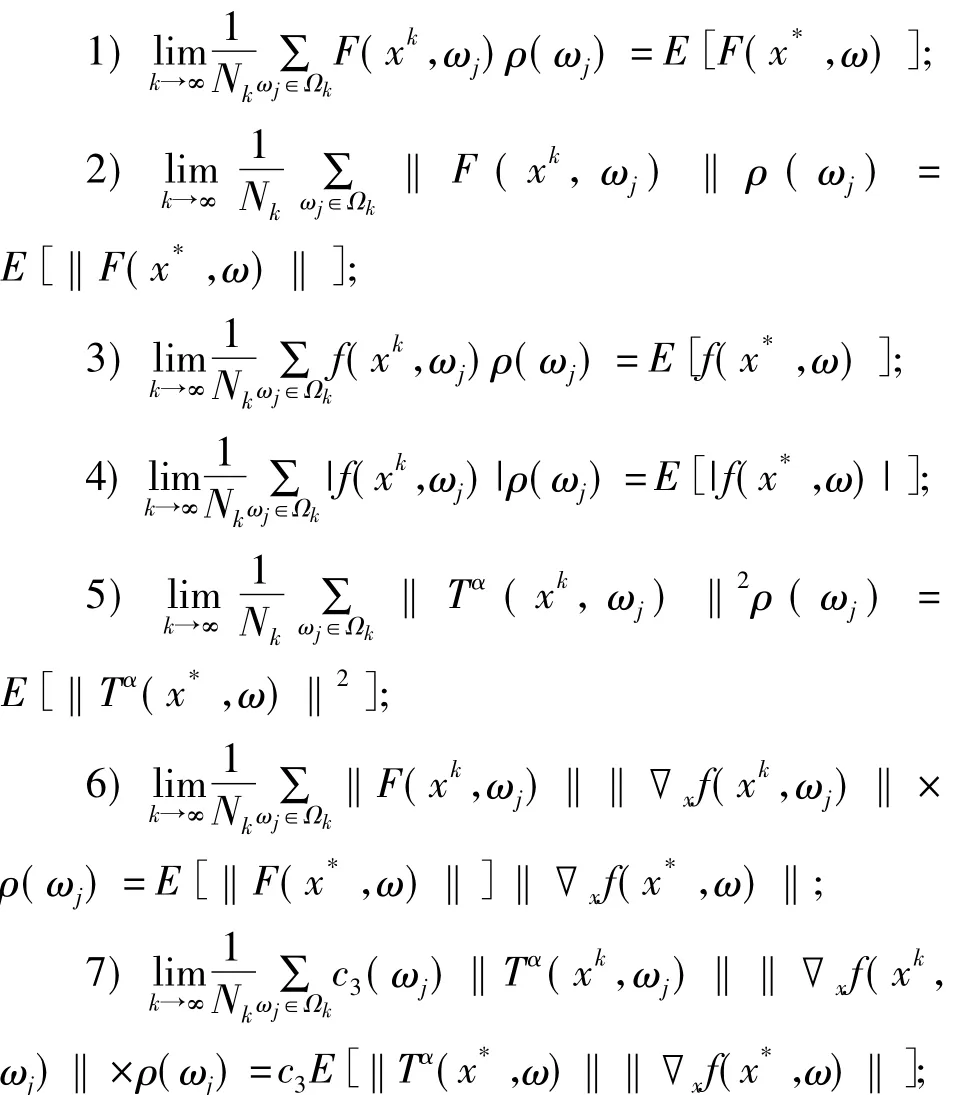
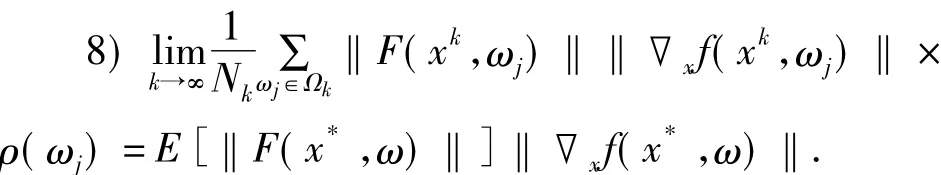
引理1．4［15］假定是非空閉集，是一開子集，f:Rn×U→R是一連續(xù)函數(shù)，其梯度fu(·，·)也是連續(xù)的．如果對于任意給定的u∈

在給出本文的主要結(jié)果之前，首先給出水平集和混合變分不等式MVI(E［F］，E［f］)的定義．對于任意的非負(fù)數(shù)c有:

混合變分不等式MVI(E［F］，E［f］)可以表述為:找x*∈K，滿足

引理1．5 如果F和f滿足假設(shè)(A)～(E)，那么混合變分不等式MVI(E［F］，E［f］)有唯一解x*∈K．

2 主要結(jié)果

定義函數(shù)如下

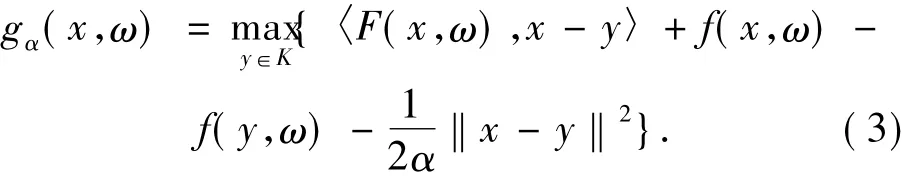
加權(quán)期望殘余極小化法可以表述為求解下面的優(yōu)化問題

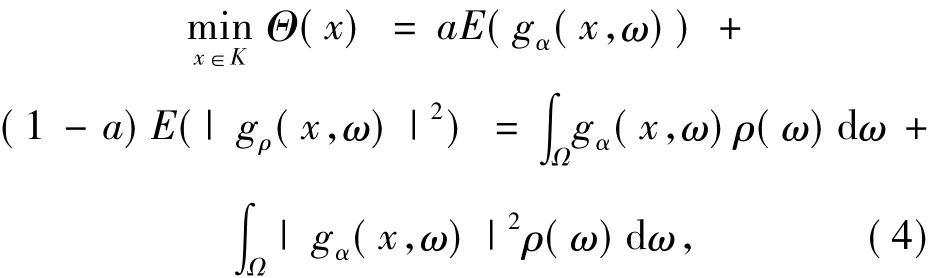
其中，1＞a＞0為權(quán)重，ρ:Ω→［0，∞)是概率密度函數(shù)，并且

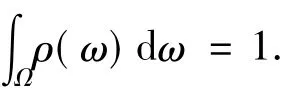
由引理1．4并結(jié)合文獻［12］中的證明方法，很容易驗證下面定理成立．

定理2．1 如果對于任意的Ω∈Ω，F(xiàn)(x，ω)關(guān)于x連續(xù)，f(x，ω)關(guān)于x是連續(xù)可微真凸函數(shù)，那么

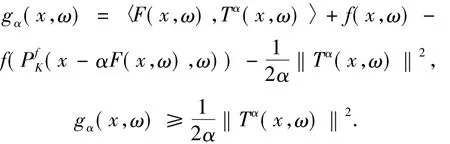
進一步，如果對于任意的Ω∈Ω，F(xiàn)(x，ω)關(guān)于x連續(xù)可微的，那么gα也是連續(xù)可微，并且有

對于問題(4)，將用擬蒙特卡洛法去求解．

令Ωk={ωj|j=1，2，…，Nk}為一列觀測集，并滿足Ωk∈Ω，當(dāng)k→∞時，Nk→∞．對于每一個k，定義

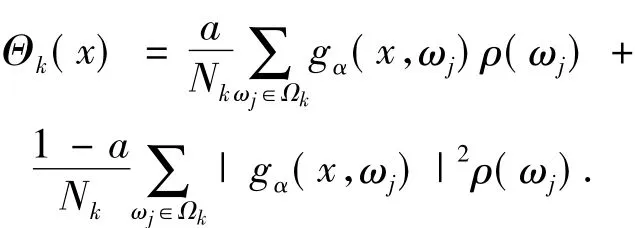
考查下面的優(yōu)化問題

記優(yōu)化問題(4)和(6)的解集為S*和

證明 由引理1．5知存在x*∈K是混合變分不等式MVI(E［F］，E［f］)的解，即滿足

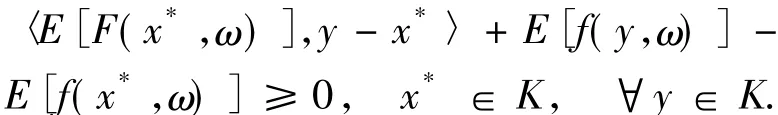
由引理1．1和1．3知

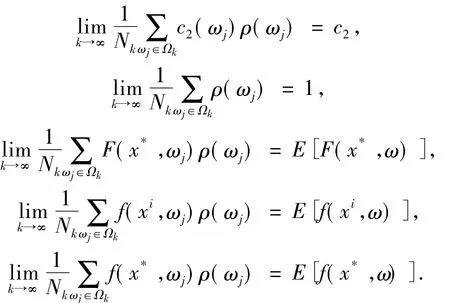
取整數(shù)，那么存在正整數(shù)k0＞0滿足:對于任意的k＞k0有下列式子成立:

現(xiàn)令k＞k0，假定存在 珋c＞0，使得水平集無界，那么存在滿足

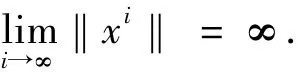
因為

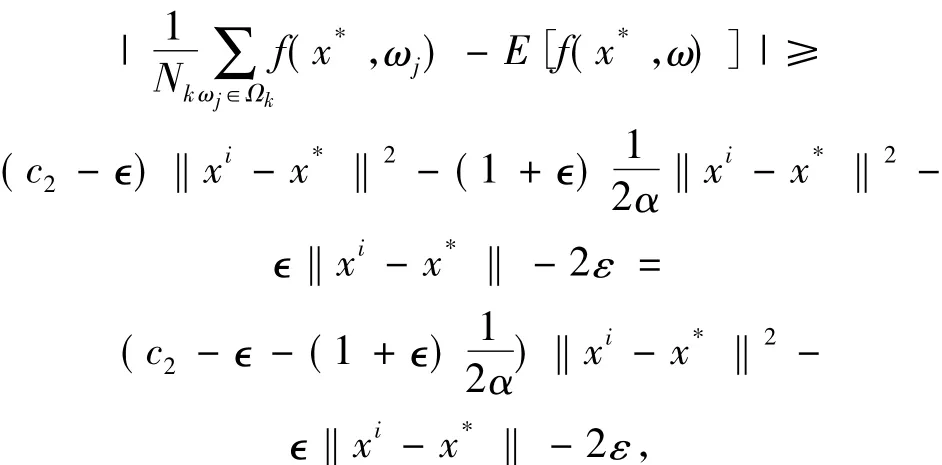
和

所以

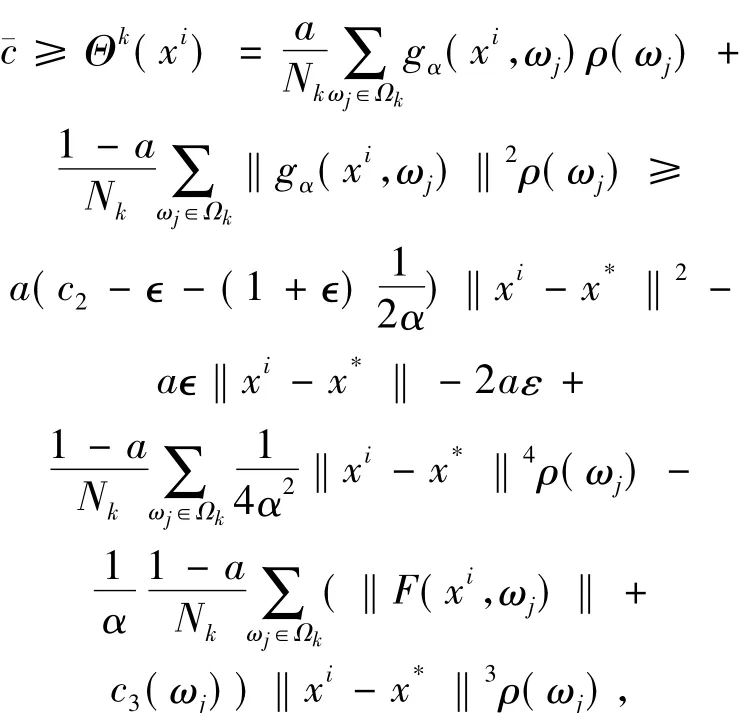
又因為

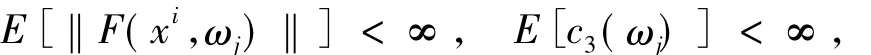
并且當(dāng)i→∞時，‖xi－x*‖∞，所以∞．這與Θk(xi)≤珋c矛盾．對于足夠大的顯然是非空有界的．

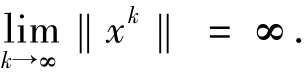
由引理1．5知存在x*∈K，從而有

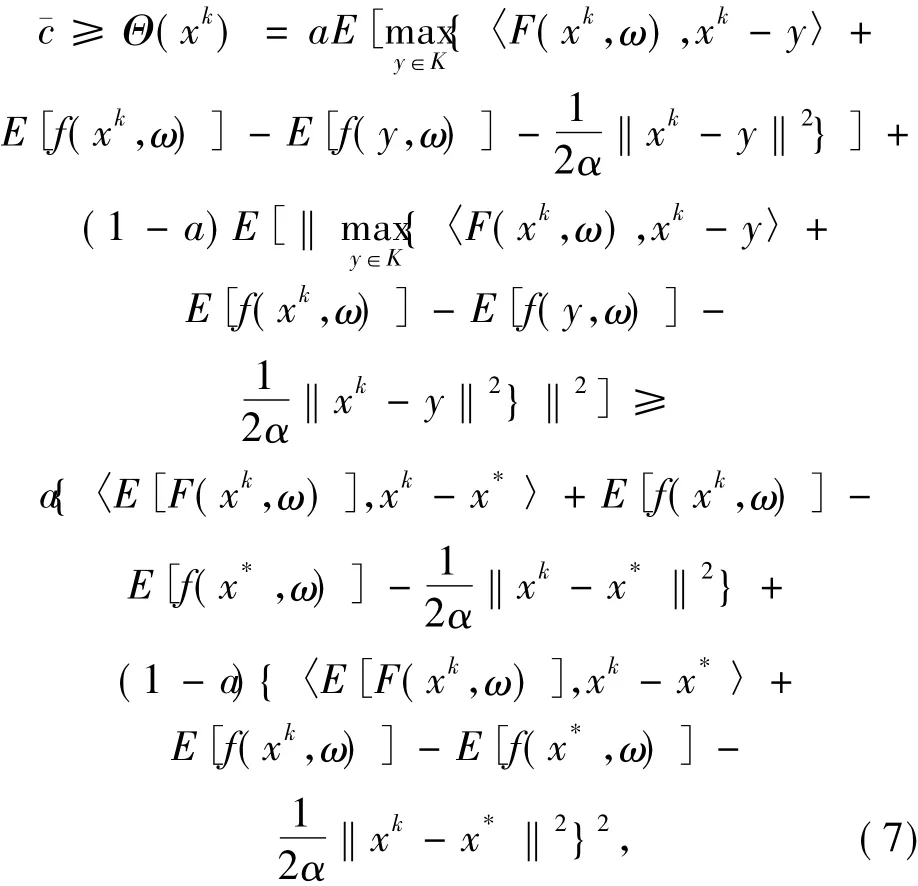
又因為

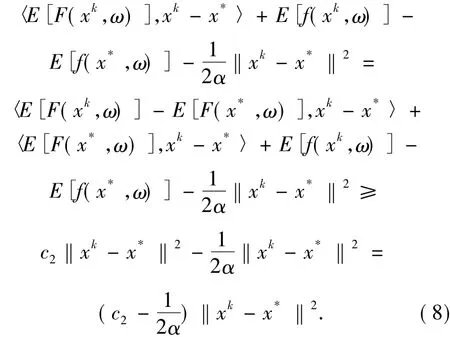
由(7)和(8)式知

因為

所以當(dāng)k→∞時，Θ(xk)→∞，這與的定義相矛盾．所以對于任意的非負(fù)數(shù)有界．

下面的定理表明，最優(yōu)問題(6)的每一個聚點都在S*中．

定理2．4 如果F和f滿足假設(shè)(A)～(E)，對于足夠大的，那么{xk}的每一個聚點都在S*中．

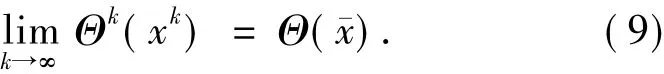
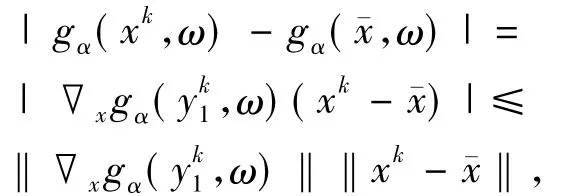
和

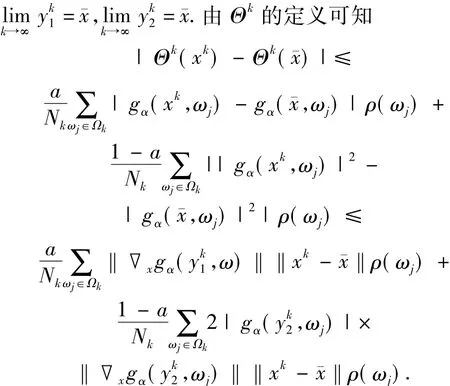
由定理2．1可知，對于任意的x，ω∈Ω有

從而可知

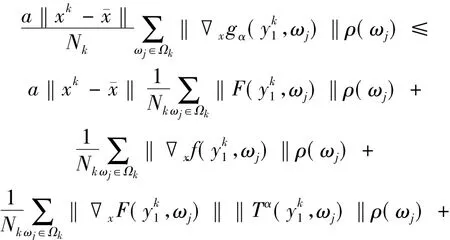
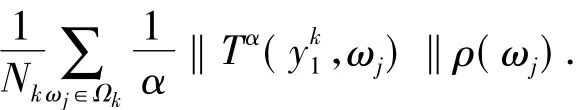
因為xk→珋x，由引理1．3知

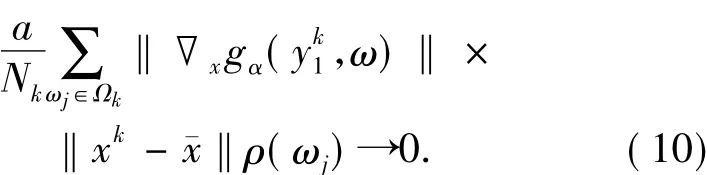
另一方面，由于對于任意的x∈K，ω∈Ω有

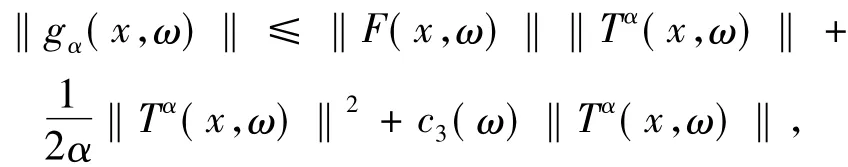
進而可知

由引理1．3知

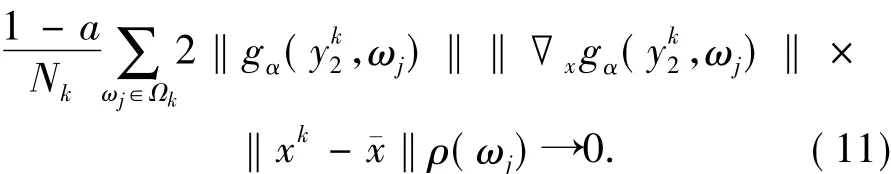
由(10)和(11)式可知

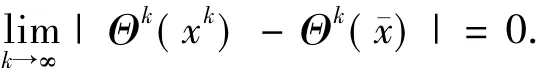
值得注意的是

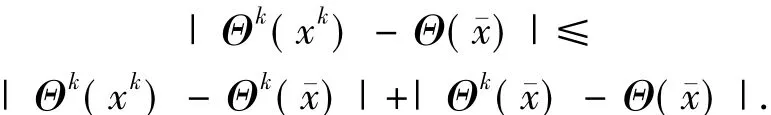
由引理1．1可知

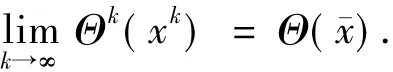
參考文獻

［1］CHEN X J，F(xiàn)UKUSHIMA M．Expected residual minimization method for stochastic linear complementarity problems［J］．Math Operations Research，2005，30:1022－1038．

［2］ ZHANG C，CHEN X J．Stochastic nonlinear complementarity problem and applications to traffic equilibrium under uncertainty［J］．J Optim Theory Appl，2008，137:277－295．

［3］LUO M J，LIN G H．Expectted residual minimization method for stochastic variational inequality problems［J］．J Optim Theory Appl，2009，140:103－116．

［4］MA H Q，HUANG N J．Expected residual minimization method for a class of stochastic quasivariational inequality problens［J］．J Appl Math，2012，2012:doi:10．1155/2012/816528．

［5］CHEN X J，WETS J B，ZHANG Y F．Stochastic variational inequalities:residual minimization smoothing sample average approximations［J］．SIAM J Optim，2012，22:649－673．

［6］FANG H，CHEN X J，F(xiàn)UKUSHIMA M．Stochastic R0matrix linear complementarity problems［J］．SIAM J Optim，2007，18:482－506．

［7］CHEN X J，ZHANG C，F(xiàn)UKUSHIMA M．Robust solution of monotone stochastic linear complementarity problems［J］．Math Programming，2009，117:51－80．

［8］JANG H，XU H．Stochastic approximation approaches to the stochastic variational inequality problems［J］．IEEE Trans Automat Control，2008，53:1462－1475．

［9］LIN G H，F(xiàn)UKUSHIMA M．New reformulations for stochastic nonlinear compelementarity problems［J］．Optim Methods and Software，2006，21:551－564．

［10］LUO M J，LIN G H．Convergence results of the ERM method for nonlinear stochastic variational problems［J］．J Optim Theory Appl，2009，142:569－581．

［11］LUO M J，LIN G H．Stochastic variational inequality problems with additional constraints and their applications in supply chain network equilibria［J］．Pacific J Optim，2011，7:263－279．

［12］MA H Q，WU M，HUANG N J，et al．Expected residual minimization method for stochastic variational inequality problem with nonlinear perturbations［J］．Appl Math Comput，2013，219:6256－6267．

［13］LU F，LI S J．Method of weighted expected residual for solving stochastic variational inequality problems［J］．Appl Math Comput，2015，269:651－663．

［14］PATRICK B．Probability and Measure［M］．New York:Wiley Interscience，1995．

［15］AUSLENDER A．Optimisation Methods Numeriques［M］．Paris:Masson，1976．

［16］MA H Q，HUANG N J，WU M，et al．A new gap function for vector variational inequalities with an application［J］．J Appl Math，2013，2013:doi:10．1155/2013/423040．

Weighted Expected Survival Minimization Method for Solving a Class of Stochastic Mixed Variational Inequality

SHA Ming’e

(Department of Mathematics，Kunming College，Kunming 650214，Yunnan)

In this paper，we consider a class of stochastic mixed variational inequalities in finite dimensional spaces．We solve stochastic mixed variational inequalities by weighted expected survival minimization method．Using the quasi-Monte Carlo method，we give the solution of weighted expected survival minimization method under some suitable conditions．

stochastic mixed variational inequality;weighted expected survival minimization method;quasi-Monte Carlo method

O176．31

A

1001－8395(2016)04－0536－06

10．3969/j．issn．1001－8395．2016．04．014

(編輯 李德華)

2015－12－01

國家自然科學(xué)基金(51402138)

沙明娥(1963—)，女，講師，主要從事數(shù)學(xué)分析與應(yīng)用模型的研究，E－mail:MingE－Sha@126．com

2010 MSC:65K10