一個自動確定信賴域半徑的錐模型信賴域方法

馮 琳，段復建

(1．重慶文理學院數學與財經學院，重慶永川402160; 2．桂林電子科技大學數學與計算科學學院，廣西桂林541004)

一個自動確定信賴域半徑的錐模型信賴域方法

馮 琳1，段復建2

(1．重慶文理學院數學與財經學院，重慶永川402160; 2．桂林電子科技大學數學與計算科學學院，廣西桂林541004)

自適應信賴域算法由于利用了對算法有重大影響的有關當前迭代點的信息，提高了算法的效率，因此對于無約束最優化問題提出一個錐模型自適應信賴域算法．算法中信賴域半徑采用新的自適應修正策略．算法在每步迭代中以R－函數變化的速率、水平向量信息以及當前迭代點的一階導數信息來修正信賴域半徑的大小，使得信賴域半徑的修正依據于問題本身，克服傳統信賴域算法中沒有利用當前迭代點的信息修正信賴域半徑的缺點．在一定的條件下簡潔地給出了算法的全局收斂性分析．算法豐富了已有的自適應信賴域算法．

無約束最優化;信賴域方法;錐模型;自適應;全局收斂性

其中，f(x):Rn→R1是連續可微函數．本文采用如下記號:‖·‖表示Euclidean范數;g(x)∈Rn是f(x)在點x的梯度;H(x)∈Rn×n是f(x)在點x的Hessian矩陣，{xk}是某一算法產生的迭代點列，并記fk=f(xk)，gk=g(xk)，Hk=H(xk);Bk∈Rn×n是對稱矩陣，它是f(x)在點xk的Hessian矩陣或其近似．

信賴域算法和線搜索方法是求解(1)式的兩類主要的數值計算方法．與線搜索方法相比，信賴域算法具有穩定的數值性能、收斂性強、迭代次數少、能有效地解決病態問題，并且不需要子問題的Hessian矩陣是正定的．因此在非線性優化界受到了特別的重視，特別是最近幾年一直是非線性優化界研究的一個熱點．

信賴域算法是一種迭代算法．在每一步迭代，求解信賴域子問題

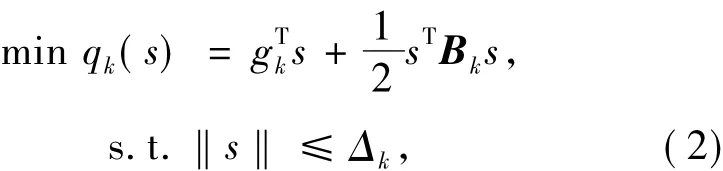
本文考慮無約束最優化問題

其中，s=x－xk，gk=f(xk)，Δk＞0是信賴域半徑．

在當前迭代點xk，設子問題(2)的解是sk，則在點xk處的實際下降量

預估下降量

實際下降量Are sk與預估下降量Pre sk的比值為

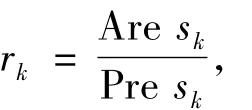
它反映了子問題(2)的解sk令人滿意的程度．rk越大，表明sk越令人滿意．如果sk令人滿意，就接受sk，得到下一個迭代點xk+1，同時增大信賴域半徑Δk;反之，則拒絕sk，同時縮小信賴域半徑Δk，重新求解子問題(2)，直至sk被接受，即

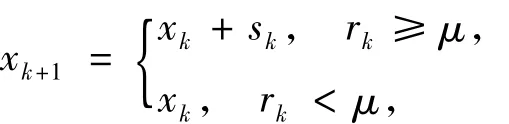
其中，μ∈(0，1)是一個常數，并調節信賴域半徑

其中，0≤μ1＜μ2＜1，0＜c1＜1＜c2是常數．

(3)式表明對信賴域半徑Δk的調節只是根據rk按常數倍放大或縮小初始信賴域半徑，沒有利用對算法有重大影響的gk、Bk等這些有關當前迭代點的信息，這樣降低了算法的效率．基于此，許多自適應信賴域方法被提出．A．Sartenaer［1］研究了初始信賴域半徑的選取對信賴域算法的影響，提出一個自動確定初始信賴域半徑的ITRR方法．J．Y．Fan等［2］提出信賴域半徑收斂到零的方法，其信賴域半徑Δk=μk‖gk‖．李紅等［3］提出一個充分利用rk的信息，利用R－函數變化的速率自動確定信賴域半徑Δk=Rη(t)‖dk－1‖的方法，其中Rη(t)是一個關于rk的R－函數．文獻［4－6］也提出了自適應信賴域方法．

定義1［7］Rη(t)定義在(－∞，+∞)上，參數η∈(0，1)，Rη(t)是一個R－函數當且僅當滿足:

(i)Rη(t)在(－∞，+∞)非減;

(iii)Rη(t)≤1－γ1(t＜η，γ1∈(0，1－β)是一個常數);

(iv)Rη(η)=1+γ2(γ2∈(0，β)是一個常數);

由定義1得到R－函數如下一些性質．

定理1［7］如果Rη(t)(η∈(0，1))是一個R－函數，則有

因此可以把Rμ(rk)作為增大或縮小信賴域半徑的尺度，使信賴域半徑的調節依據于問題本身．

大多數信賴域算法采用二次模型逼近原問題f(x)，但對一些非二次性態強、曲率變化劇烈的函數，采用二次模型逼近原問題效果較差，因此得到的最優點較差．W．C．Davidon［8］首次提出錐模型．錐模型比二次模型更一般，包含的信息和自由度更多，更能充分地逼近原問題f(x)，因而吸引了許多學者對它進行研究．文獻［9－11］研究了錐模型共線調比擬牛頓方法．諸梅芳等［12］提出求解(1)的錐模型信賴域算法;Q．Ni［13］給出錐模型信賴域子問題的最優性條件，為錐模型信賴域子問題的求解提供了更充分、合理的理論基礎，信賴域算法進一步發展．文獻［14－16］提出了錐模型非單調信賴域算法．文獻［17］提出了錐模型回溯過渡信賴域算法．J．H．Fu等［18］將自適應技術引入錐模型信賴域算法，提出錐模型自適應信賴域算法［19－25］;王希云等［26］也提出錐模型自適應信賴域算法，信賴域半徑

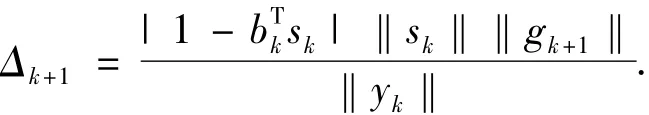
錐模型信賴域算法得到了廣泛的發展，并且數值結果表明對一些函數，特別是對曲率變化劇烈的函數，錐模型信賴域算法比二次模型信賴域算法效果更好．

求解(1)式的一個典型的錐模型信賴域子問題是

其中，bk∈Rn是水平向量，．當bk=0或時，錐模型轉化為二次模型，因此錐模型是二次模型的推廣．

在文獻［2－3，26］工作的基礎上，基于錐模型信賴域子問題(6)，本文提出一類新的自動確定信賴域半徑的信賴域方法．每次迭代，令使得在每次迭代，依據問題本身的信息自動調節信賴域半徑．

1 自動確定信賴域半徑的錐模型信賴域方法

基于錐模型信賴域子問題(6)和新的信賴域半徑(7)，給出一個求解(1)式的自適應信賴域方法．

設(6)式的解為sk，則目標函數f(x)在第k步的實際下降量為

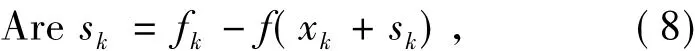
預估下降量為

比值

具體的自動確定信賴域半徑的錐模型信賴域方法實現如下．

算法1 第1步 給出初始點x0∈Rn，Δ0＞0，b0∈Rn×1，ε＞0，0＜μ＜1，0＜β＜1，0＜γ1＜1－β，γ2＞0，M＞1+γ2，B0=I(單位陣)，k:=0．

第2步 計算gk=g(xk)．如果‖gk‖≤ε，則停止計算，x*=xk;否則，轉第3步．

第3步 近似求解(6)式得到sk，并利用(8)～(10)式分別計算Are sk、Pre sk、rk．

第4步 如果rk＜μ，令xk+1=xk;否則，令xk+1=xk+sk．

第5步 修正bk及Bk，產生bk+1及Bk+1，利用(7)式計算Δk+1．令k:=k+1，轉第2步．

注1．1 (i)算法1中，要求‖bk‖Δk＜1，如果‖bk‖Δ≥1，則令，使得‖bk‖Δk＜1．

(ii)算法1第3步中sk的具體求解及第5步中bk和Bk的校正公式可參見文獻［18］．

(iii)若(6)和(7)式中的bk=0，則算法1轉化為相應的自動確定信賴域半徑的二次模型信賴域方法．

(iv)算法1中，利用(3)式調節信賴域半徑，得到傳統的錐模型信賴域算法．

2 算法的收斂性

在一定的條件下證明算法1的全局收斂性．

本文所需假設如下:

(A1)水平集L(x0)={x|f(x)≤f(x0)}有界，f(x)在L(x0)上二階連續可微;

(A2){Bk}、{}、{bk}一致有界，即存在常數δ1，δ2，δ3＞0，使得對k有‖Bk‖≤δ1，‖‖≤δ2，‖bk‖≤δ3;

(A3)g(x)是Lipschitz連續函數，即存在L＞0，滿足

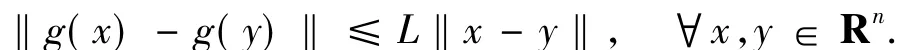
為討論方便，記I={k:rk＜μ}，J={k:rk≥μ}．

引理1 設sk是子問題(6)的解，gk≠0，則有

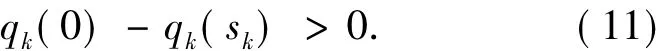
為得到算法的下降性條件，引入Cauchy點

其中

引理2 對Cauchy點pck滿足

證明 分3種情況證明．

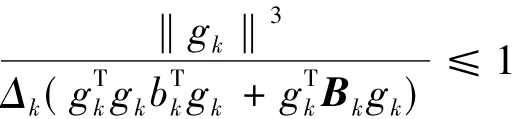
時

則有

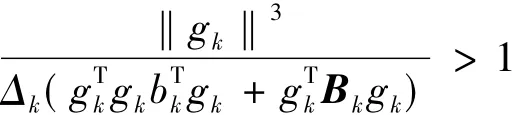
時3

由‖Bk‖Δk＜1知

則有

由(13)～(16)式知

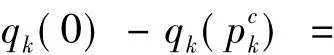
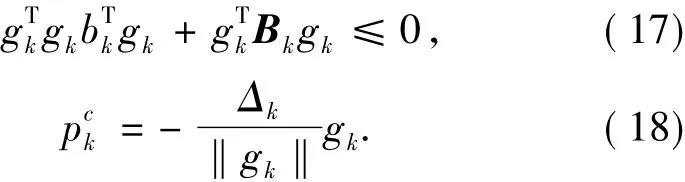
由(17)式知

于是

從而

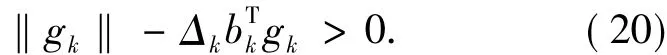
由(17)式知

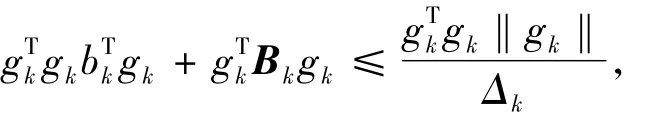
于是

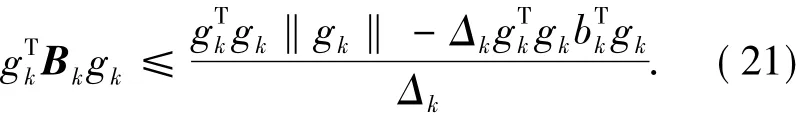
又

由(21)和(22)式知

于是由(18)、(23)式和(ii)的過程，(19)和

(20)式知

證畢．

下面的引理說明子問題(6)的解sk滿足充分下降條件．

引理3 設sk是子問題(6)的解，則有

證明 由引理2知

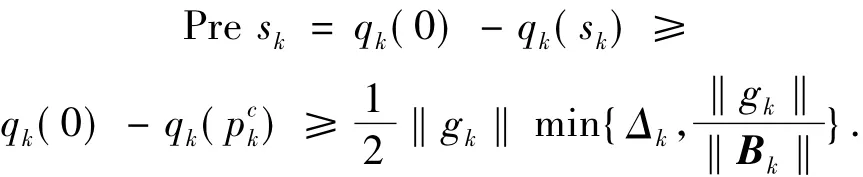
引理4 如果假設(A1)～(A3)成立，則存在常數c＞0，使得

證明 由(5)和(7)式及‖bk‖Δk＜1知

令c=2M，則Δk≤c‖gk‖，從而‖sk‖≤c‖gk‖．

引理5 如果{xk}是由算法1產生的點列，則

證明 用數學歸納法證明．

當k=0時，f(x0)≤f(x0)，則x0∈L(x0)，命題成立．

下證假設xk∈L(x0)時，則有xk+1∈L(x0)．

當xk∈L(x0)時，有f(xk)≤f(x0)．

(i)如果k∈I，則rk＜μ．

由算法1第4步知:xk+1=xk，于是 f(xk+1)= f(xk)．所以f(xk+1)≤f(x0)．

(ii)如果k∈J，則rk≥μ．于是由(11)式知

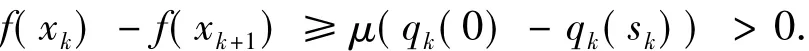
因而f(xk+1)≤f(xk)．所以f(xk+1)≤f(x0)．

由(i)和(ii)知:當xk∈L(x0)時，xk+1∈L(x0)．

由數學歸納法知:結論成立．

算法1中，如果xk+1=xk+sk，則稱xk+1是一個成功的迭代點;如果xk+1=xk，則稱xk+1是一個非成功的迭代點．

引理6 如果假設(A1)～(A3)成立，{xk}是由算法1產生的無窮點列，且對k有‖gk‖＞ε，ε∈(0，1)是常數，則對，存在非負整數p使得xk+p+1是一個成功的迭代點．

證明 假設存在非負整數 k0使得p都有xk0+p+1是一個非成功的迭代點，即

由算法1第4步知

由(4)和(7)式知

于是

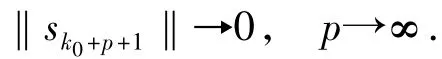
因而對充分大的p有 1

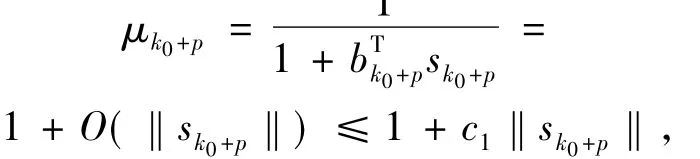
其中c1為某一常數．

于是對充分大的p有

由(24)式知

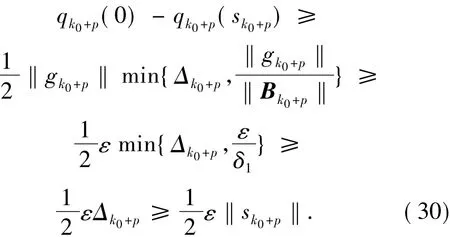
由f(x)是連續可微函數及Taylor展開式知

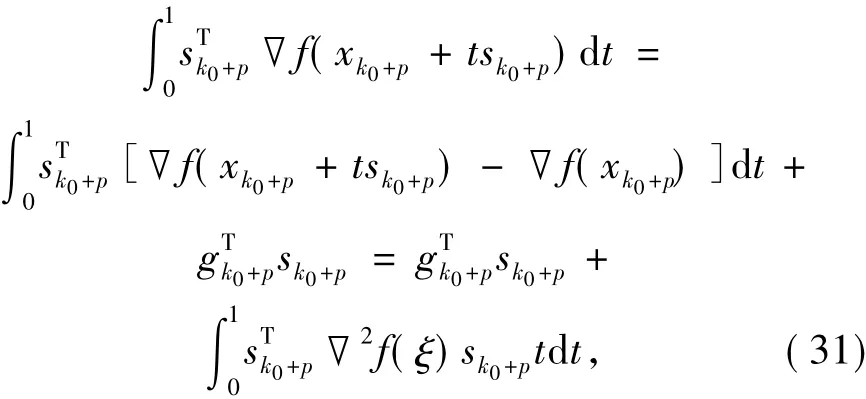
其中

由于f(x)二階連續可微，則對x∈{x|f(x)≤f(x0)，x∈Rn}，α＞0，s．t．‖2f(x)‖≤α．

由(29)～(31)式知

從而當p充分大時

由0＜μ＜1知:當p充分大時，rk0+p≥μ，這與(26)式矛盾．

定理2 如果假設(A1)～(A3)成立，算法1產生無窮點列{xk}，則有

證明 (反證法)假設結論不成立，則存在常數ε＞0，ε∈(0，1)，使得‖gk‖≥ε，k．

下證

由引理6知:當k充分大時，則k∈J，此時有

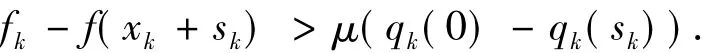
由于{fk}單調遞減有下界，因此{fk}收斂．

于是當k充分大時有

因為‖bk‖Δk＜1;當‖bk‖Δ≥1，則(0＜α＜1)，因此τ＞0，使得‖bk‖Δk≤τ．于是

所以

由(34)式知

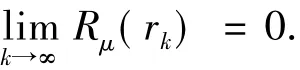
又k∈J時，有rk≥μ，由定義1和定理1知:，使得，這與(33)式矛盾．因此定理成立．

3 結論

對于無約束最優化問題提出了一個基于錐模型的自適應信賴域算法．信賴域半徑采用一個新的自適應修正策略．算法在每步迭代中以R－函數變化的速率、水平向量信息以及當前迭代點的一階導數信息來修正信賴域半徑的大小，使得信賴域半徑的修正依據于問題本身，克服了傳統信賴域算法中沒有利用當前迭代點的信息修正信賴域半徑的缺點．在一定的條件下給出了新算法的全局收斂性分析．

致謝 重慶文理學院校級基金(Y2013SC42)對本文給予了資助，謹致謝意．

［1］SARTENAER A．Automatic determination of an initial trust region in nonlinear programming［J］．SIAM J Scientific Computing，1997，18:1788－1803．

［2］FAN J Y，AI W B，ZHANG Q Y．A line search and trust region algorithm with trust region radius convergence to zero［J］．J Comput Math，2004，22(6):865－872．

［3］李紅，焦寶聰．一類帶線搜索的自適應信賴域算法［J］．運籌學學報，2008，12(2):97－104．

［4］SANG Z Y，SUN Q Y．A self－adaptive trust region method with line search based on a simple subproblem model［J］．J Comput Appl Math，2009，232:514－522．

［5］馮琳，段復建．無約束優化的一個濾子非單調信賴域算法［J］．四川師范大學學報(自然科學版)，2015，38(2):223－229．

［6］朱帥，朱世昕，王希云．基于新錐模型的帶固定步長的非單調自適應信賴域算法［J］．西南民族大學學報(自然科學版)，2012，38(1):44－49．

［7］HEI L．A self－adaptive trust region algorithm［J］．J Comput Math，2003，21:229－236．

［8］DAVIDON W C．Conic approximations and collinear scaling for optimizers［J］．SIAM J Numer Anal，1980，17(2):268－281．

［9］SORENSON D C．The Q－superlinear convergence of a collinear scaling algorithm for unconstrained optimization［J］．SIAM J Numer Anal，1980，17:84－114．

［10］ARIYAWANSA K A．Deriving collinear scaling algorithms as extension of quasi－Newton methods and the local convergence of DFP and BFGS－related collinear scaling algorithms［J］．Math Prog，1990，49:23－48．

［11］SHENG S．Interpolation by conic model for unconstrained optimization［J］．Computing，1995，54:83－98．

［12］諸梅芳，薛毅，張鳳圣．錐模型的擬NEWTON型信賴域方法［J］．高等學校計算數學學報，1995，17(1):36－47．

［13］NI Q．Optimality conditions for trust－region subproblems involving a conic model［J］．SIAM J Optim，2005，15(3):826－837．

［14］QU S J，JIANG S D，ZHU Y．A conic trust－region method and its convergence properties［J］．Comput Math Appl，2009，57: 513－528．

［15］CUI Z C，WU B Y，QU S J．Combining nonmonotone conic trust region and line search techniques for unconstrained optimization［J］．J Comput Appl Math，2011，235:2432－2441．

［16］JI Y，LI Y J，ZHANG K C，et al．A new nonmonotone conic trust－region method of conic model for solving unconstrained optimization［J］．J Comput Appl Math，2010，233:1746－1754．

［17］葛恒武．無約束優化問題的錐模型回溯過濾信賴域算法［J］．蘇州大學學報(自然科學版)，2010，26(2):8－15．

［18］FU J H，SUN W Y，RAIMUNDO J B De Sampaio．An adaptive approach of conic trust－region method for unconstrained optimization problems［J］．Appl Math Comput，2005，19(1/2):165－177．

［19］ZHANG J，ZHANG K，QU S．A nonmonotone adaptive trust region method for unconstrained optimization based on conic model［J］．Appl Math Comput，2010，217(8):4265－4273．

［20］孫文瑜，徐東．解無約束最優化的基于錐模型的過濾集－信賴域方法［J］．中國科學，2012，42(5):527－543．

［21］ZHAO L．Non－monotone adaptive filter conic trust region method for unconstrained optimization［J］．J Math Comput Sci，2012(6):1874－1893．

［22］李小偉，錢慧敏．帶有線搜索的非單調自適應新錐模型信賴域算法［J］．電子科技，2013，26(11):4－6，46．

［23］ZHOU Q，ZHOU F，CAO F．A nonmonotone trust region method based on simple conic models for unconstrained optimization［J］．Appl Math Comput，2013，225(12):295－305．

［24］CUI Z．A nonmonotone adaptive trust region method based on conic model for unconstrained optimization［J］．J Optimization，2014，2014:1－8．

［25］ZHOU Q，ZHANG．An adaptive trust region method based on simple conic models［J］．J Math Modelling Algorithms in Operations Research，2015:1－15．

［26］王希云，王慶．一種基于新錐模型的自適應信賴域算法［J］．應用數學，2010，23(2):307－312．

A Trust Region Method with Automatic Determination of the Trust Region Radius Based on the Conic Model

FENG Lin1，DUAN Fujian2

(1．School of Mathematics and Finance，Chongqing College of Arts and Sciences，Yongchuan 402160，Chongqing; 2．School of Mathematics and Computational Science，Guilin University of Electronic Technology，Guilin 541004，Guangxi)

In this paper，we propose a self-adaptive trust region method based on the conic model for unconstrained optimization problems．The trust region radius is updated with a new self-adaptive strategy．At every iteration，the trust region radius is updated at the variable rate of R-function，the level vector information and the first order derivative information at the current point，thus the updation of the trust region radius is dependent of the problem itself，which overcomes the shortcoming，that the information at the current point in the traditional trust region algorithms is not applied．The global convergence of the new method is briefly analyzed under mild conditions．The method enriches the existing self-adaptive trust region methods．

unconstrained optimization;trust region method;conic model;self-adaptive;global convergence

O224．2

A

1001－8395(2016)04－0542－07

10．3969/j．issn．1001－8395．2016．04．015

(編輯 李德華)

2014－07－03

國家自然科學基金(11061011)和廣西自然科學基金(2011GXNSFA018138)

馮 琳(1973—)，女，講師，主要從事最優化理論與算法的研究，E－mail:fenglin730825@126．com

2010 MSC:90C30;65K10