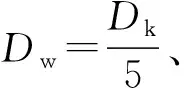七溝道球籠式等速萬向節溝道接觸應力的計算及優化設計
石寶樞,郭靜芬
(1. 浙江眾達傳動股份有限公司,浙江 金華 321025;2. 洛陽軸研科技股份有限公司,河南 洛陽 471039;3.河南省高性能軸承技術重點實驗室,河南 洛陽 471039;4.滾動軸承產業技術創新戰略聯盟,河南 洛陽 471039)
符號說明
dz—— 傳動軸公稱直徑,mm
Dw——鋼球直徑,mm
Dpw—— 球組節圓直徑,mm
Dk——鐘形殼最大外徑,mm
E0——鋼球的彈性模量,MPa
E1——星形套的彈性模量,MPa
E2——鐘形殼的彈性模量,MPa
Ei——星形套的當量彈性模量,MPa
Ee——鐘形殼的當量彈性模量,MPa
Eki——星形套圓弧形溝道與相應鋼球接觸的第二類橢圓積分
Eke——鐘形殼圓弧形溝道與相應鋼球接觸的第二類橢圓積分
fi——星形套圓弧形溝道截面曲率半徑系數
fe——鐘形殼圓弧形溝道截面曲率半徑系數
KD——球組節圓直徑系數
ki——星形套圓弧形溝道與相應鋼球接觸的橢圓系數
ke——鐘形殼圓弧形溝道與相應鋼球接觸的橢圓系數
Li——星形套圓弧形溝道與相應鋼球接觸點距鋼球回轉中心的的距離,mm
Le——鐘形殼圓弧形溝道與相應鋼球接觸點距鋼球回轉中心的的距離,mm
pimax——星形套圓弧形溝道與相應鋼球的最大接觸應力,MPa
pemax——鐘形殼圓弧形溝道與相應鋼球的最大接觸應力,MPa
Qi——星形套圓弧形溝道與相應鋼球的接觸載荷,N
Qe——鐘形殼圓弧形溝道與相應鋼球的接觸載荷,N
Ri——星形套圓弧形溝道截面曲率半徑,mm
Re——鐘形殼圓弧形溝道截面曲率半徑,mm
∑Ri——星形套圓弧形溝道主曲率半徑和,mm
∑Re——鐘形殼圓弧形溝道主曲率半徑和,mm
T——七溝道球籠式等速萬向節所傳遞的轉矩,N·mm
ν0——鋼球材料的泊松比
ν1——星形套材料的泊松比
ν2——鐘形殼材料的泊松比
球籠式等速萬向節傳遞扭矩和旋轉運動,通過位于星形套和鐘形殼若干個素線為圓弧形的溝道和相同數量的一組鋼球共軛接觸而實現。星形套和鐘形殼溝道與相應的鋼球均承受接觸載荷,故接觸應力是決定球籠式等速萬向節可靠性和壽命的重要因素。而星形套和鐘形殼的溝道截面形狀有圓弧、雙偏心圓弧和橢圓等若干種,文中僅探討圓弧形溝道截面。
七溝道球籠式等速萬向節是該類產品技術的重要突破和優化設計的最終選擇[1],但仍需要對星形套和鐘形殼圓弧形溝道與相應鋼球的接觸應力進行系統分析與定量計算,進而對2種圓弧形溝道的結構主參數進行優化,以進一步提高七溝道球籠式等速萬向節的可靠性和壽命。
1 圓弧形溝道的曲率
溝道截面為圓弧形的星形套和鐘形殼與相應鋼球的接觸如圖1所示,O為鋼球的中心,O1為星形套某溝道截面的曲率中心,O2為鐘形殼某溝道截面的曲率中心,O3為星形套與鐘形殼的球組節圓中心(鋼球回轉中心)。溝道截面的曲率半徑與相應的鋼球直徑之比稱為該溝道截面的曲率半徑系數。
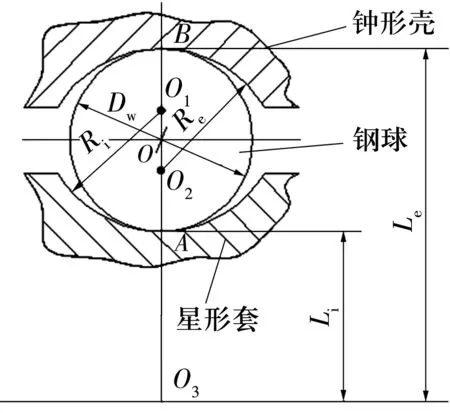
圖1 球籠式等速萬向節的圓弧形溝道
星形套圓弧形溝道截面曲率半徑為
Ri=fiDw,
(1)
鐘形殼圓弧形溝道截面曲率半徑為
Re=feDw。
(2)
由圖1可知,星形套、鐘形殼圓弧形溝道與相應鋼球接觸點(溝道底部)距鋼球回轉中心的距離分別為
(3)
(4)
星形套、鐘形殼圓弧形溝道的主曲率和分別為[2]
(5)
。(6)
2 接觸應力計算
根據Hertz接觸理論,假定理想狀態下作用在每個鋼球上的力均相等,接觸區處于彈性應力狀態,且接觸點的尺寸比接觸點的曲率半徑小。
設七溝道球籠式等速萬向節所傳遞的轉矩為T, 7個均布且直徑相等的鋼球均同時受載。理想狀態下7個鋼球上傳遞力的大小均相等,則作用在星形套圓弧形溝道與相應鋼球接觸點的接觸載荷為
(7)
鐘形殼圓弧形溝道與相應鋼球接觸點的接觸載荷為
(8)
當接觸點的主曲率、法向載荷、彈性模量和材料的泊松比已知時,用Hertz接觸理論可求得接觸橢圓的長、短半軸,進而可求得最大接觸應力[2]。
星形套圓弧形溝道與相應鋼球的最大接觸應力為
(9)
由(7)式、(9)式得星形套圓弧形溝道與相應鋼球的最大接觸應力為
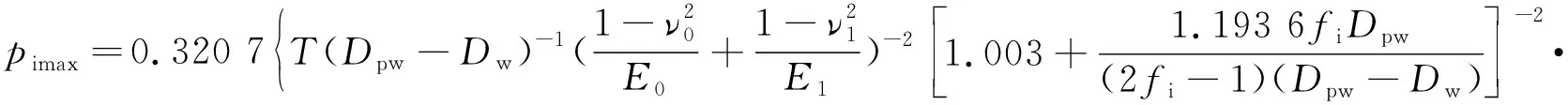
(10)
鐘形殼圓弧形溝道與相應鋼球的最大接觸應力為
(11)
由(8)式、(11)式可得鐘形殼圓弧形溝道與相應鋼球的最大接觸應力為

(12)
3 溝道結構主參數的正交試驗及分析
3.1 正交試驗方案及結果
由(10)式和(12)式可得,七溝道球籠式等速萬向節星形套和鐘形殼圓弧形溝道與相應鋼球的接觸應力(或承載能力)與鋼球直徑Dw、球組節圓直徑Dpw、2種圓弧形溝道截面曲率半徑系數fi(或fe)有關。星形套和鐘形殼圓弧形溝道與相應鋼球的最大接觸應力pimax(或pemax)是以結構主參數Dw,Dpw,fi(或fe)為自變量的多元函數。要探討的是自變量Dw,Dpw,fi(或fe)如何取值,使得pimax(或pemax)最小。為便于分析,分別取1個自變量(另2個自變量均視為常數),分別探討其對最大接觸應力pimax(或pemax)的影響,即分別求pimax(或pemax)的方向導數。因(10)式、(12)式非常復雜,其變化規律難以用方向導數來表達。現參考文獻[3],通過正交試驗探討。
現以鋼球直徑Dw、球組節圓直徑Dpw和溝道截面曲率半徑系數fi(或fe)這3個參數為正交試驗因素,以溝道最大接觸應力值pimax(或pemax)為性能指標進行正交試驗。
設某規格的七溝道球籠式等速萬向節傳遞的最大轉矩(靜態額定轉矩)T=1 887 N·m,Dw=17.463 mm,Dpw=60 mm,星形套和鐘形殼圓弧形溝道截面曲率半徑系數為fi=fe=0.515;鋼球材料為GCr15,E0=206 GPa,ν0=0.29;星形套材料為20CrMnTi,E1=206 GPa,ν1=0.29;鐘形殼材料為55#鋼,E2=206 GPa,ν2=0.30。
每個因素取3種水平,其正交試驗的因素與水平見表1。正交試驗組合方案及計算結果見表2。
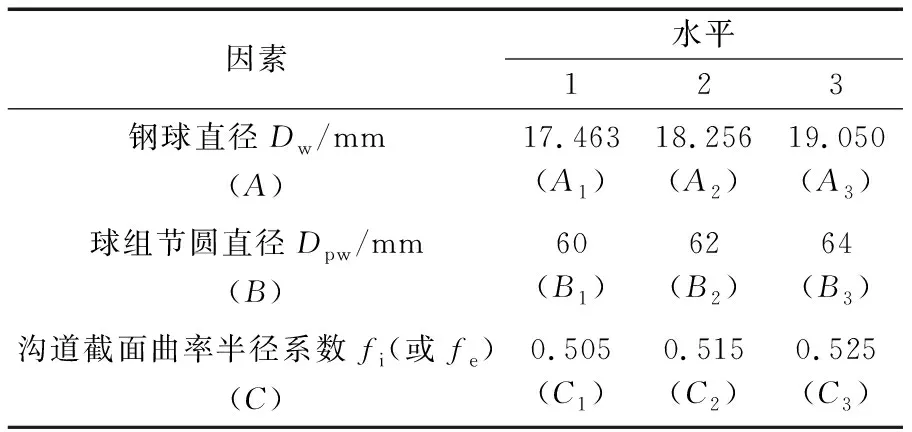
表1 溝道接觸應力正交試驗優化設計因素與水平
由表2的各列因素A,B,C,可分別計算出星形套、鐘形殼溝道接觸應力每種水平試驗值的平均值及極差,結果見表3。
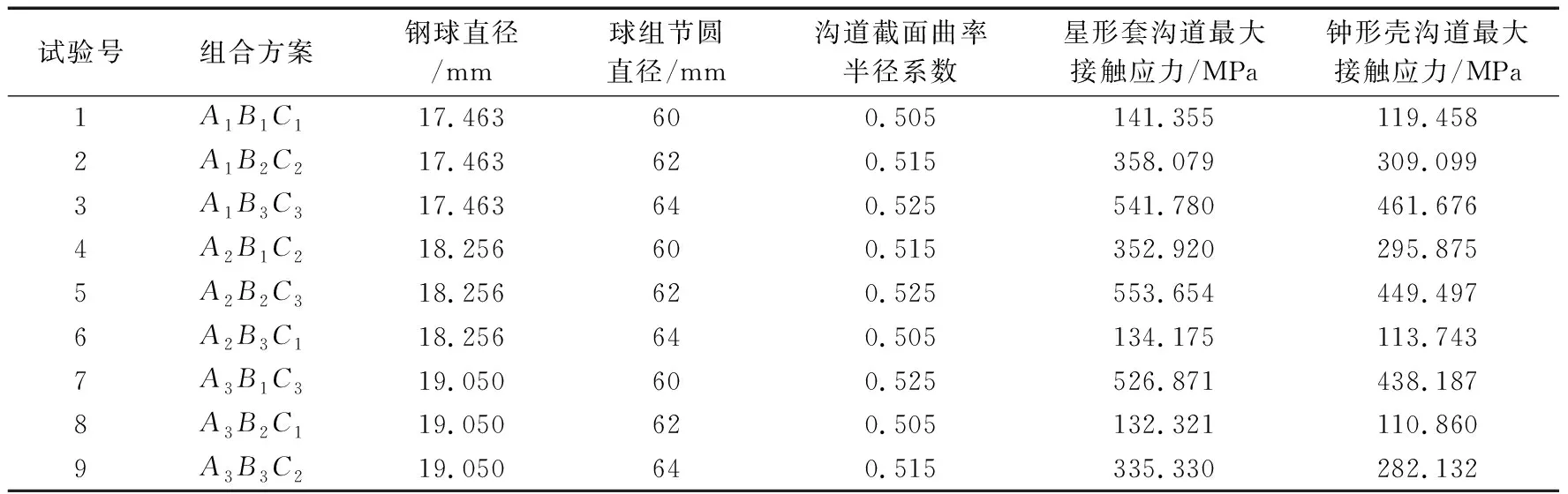
表2 溝道接觸應力正交試驗及計算結果

表3 溝道接觸應力平均值及極差
3.2 極差分析
星形套和鐘形殼溝道截面曲率半徑系數fi(或fe)的極差遠大于鋼球直徑Dw和球組節圓直徑Dpw的極差。由此可見,星形套和鐘形殼溝道截面曲率半徑系數對七溝道球籠式等速萬向節溝道的接觸應力(或承載能力)的影響極其顯著,遠遠大于鋼球直徑和球組節圓直徑的影響。
3.3 試驗分析
接觸應力平均值與主參數的關系如圖2~圖4所示。
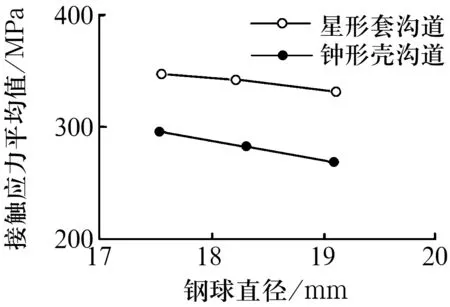
圖2 接觸應力平均值與鋼球直徑的關系
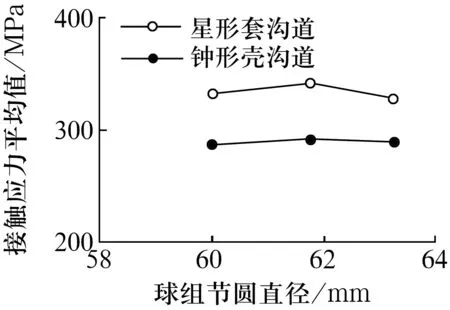
圖3 接觸應力平均值與球組節圓直徑的關系
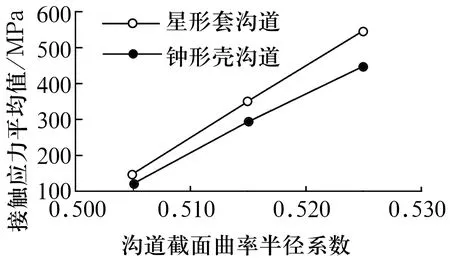
圖4 接觸應力平均值與溝道截面曲率半徑系數的關系
由圖可知,星形套溝道的接觸應力總大于鐘形殼溝道的接觸應力(或承載能力),即鐘形殼的承載能力總大于星形套的承載能力,星形套是薄弱環節。現分別討論3個結構主參數對七溝道球籠式等速萬向節的接觸應力的影響。
3.3.1 鋼球直徑
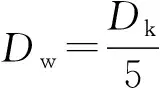
3.3.2 球組節圓直徑
由表2和圖3可知,球組節圓直徑越大,星形套和鐘形殼的接觸應力越小,承載能力越大。但接觸應力和承載能力的變化幅度較小,若球組節圓直徑增加5%,承載能力約提高1.5%。顯然,適當增大球組節圓直徑能提高七溝道球籠式等速萬向節承載能力和壽命。同樣球組節圓直徑Dpw不宜過大,經計算Dpw=KD(Dk+dZ)(KD=0.54~0.55),或者Dpw=3.5Dw為最優。
3.3.3 溝道截面曲率半徑系數
由表2和圖4可知,星形套和鐘形殼溝道截面曲率半徑系數越小,星形套和鐘形殼的接觸應力越小,承載能力越大,且接觸應力和承載能力的變化幅度大,若星形套和鐘形殼溝道曲率半徑系數減小1%,承載能力約提高60%。由此可見,適當減小星形套和鐘形殼溝道截面曲率半徑系數,可顯著地提高七溝道球籠式等速萬向節的承載能力。星形套和鐘形殼溝道曲率半徑系數為0.505是七溝道球籠式等速萬向節優化設計的結果。
4 結論
1)七溝道球籠式等速萬向節的承載能力和壽命與鋼球直徑、球組節圓直徑、星形套和鐘形殼溝道截面曲率半徑系數均有關。
2)七溝道球籠式等速萬向節星形套溝道的接觸應力總是大于鐘形殼的接觸應力,即鐘形殼承載能力大于星形套的承載能力。