高職數學教學中遷移理論的應用

孫豫　楊青駐馬店職業技術學院　（駐馬店463000）

?

高職數學教學中遷移理論的應用

孫豫楊青
駐馬店職業技術學院（駐馬店463000）

摘要高職數學教學中遷移理論的應用，應從認知結構、學生智力分析上探討遷移理論的影響因素，并從學科特點激發學生的學習潛力，增強學生對數學思想及數學方法的應用能力。

關鍵詞高職；數學教學；遷移理論；認知結構；教學應用中圖分類號：G40-01

文獻標識碼：A

文章編號：1003-3319（2016）01-00053-02

“高等數學”是培養學生數學思維、邏輯思維、計算能力和創新意思的重要學科，遷移理論在高職數學教學中的應用，可以更好地促進學生數學素養的完成。

1　遷移理論在高數中的應用價值

學習是一個連續的過程，對于學習者來說，原有知識、結構、技能和態度的整合，正是遷移理論形成的關鍵［1］。一般將遷移分為正遷移、負遷移兩類。正遷移對學生的學習具有積極的促進作用，而負遷移反而影響了學生對知識的正確認知，不足以解決問題。現代遷移理論研究發現，對于學生認知結構的影響因素較多，而有意義的學習最為關鍵。奧蘇貝爾在解釋遷移理論時提出“遷移不是孤立地建立在A、B之間，對于學習A后的最新經驗，并非是對課題B之間的直接刺激，而是間接影響學生對新知識的學習和理解”［2］。

2　高職階段學生身心發展特點

高職教育重在提升學生的職業能力，而全面探究高職學生的身心發展特點，對于貼近教學需求，改進教學方法意義重大。總的來看，其特點表現在四個方面。

2.1年齡智力特點

高職生年齡段介于18—22歲，其智力模式達到成熟期，機械記憶能力達到高峰，注意力也獲得較快發展；心理認知上自閉性與交往欲相抗衡，求知欲與識別欲不成正比，在追求理想中忽視現實；知識積累上具備一定理解和分析能力，但對實物的抽象思維及創造力不足；自我意識相對強烈。

2.2生源質量特點

從高職生的來源主要有普高、單招學生組成，生源質量總體不高，且參加不齊，一部分學生基礎不扎實，學習自信不夠；一部分學生學習習慣不好，缺乏自控力；一部分學生愛好廣泛，但缺乏鉆研精神。

2.3學習觀、就業觀特點

高職教育作為培養社會技能型人才的重要載體，對畢業、就業具有較強的方向性；在知識學習及能力培養上更傾向于職業崗位要求。

2.4對高等數學認知上的特點

從數學認知上來看，高職學生的數學知識及數學能力相對較弱，對數學學科學習積極性普遍不高，特別是對于數學理論、數學概念、數學命題缺乏深刻理解，解題易出錯；在數學知識層次上，對數學知識的關聯度、解決數學問題的積極性不夠；缺乏對數學知識的深入思考，對數學知識的理解以聽懂為主，對數學應用問題，特別是數學思維能力的應用缺乏信心。

3　影響高職學生數學學習正遷移的因素分析

遷移理論中的正遷移是促進學生學習習慣的有效動力，針對當前高職階段數學教學現狀，影響高職學生數學學習正遷移的因素主要表現在客觀及主觀兩個方面。

3.1客觀方面的因素

心理學研究發現，對于學生在數學知識的學習中，如果所選用的教材與學生過去所學知識具有相似性，則有助于增強學生的學習興趣。奧蘇貝爾認知結構遷移理論也提出“先行組織者”教學，就是將學習任務與新舊知識的銜接來構成學習的層次性，促進學生正向遷移。再者，對于課堂教學環境，民主、和諧、平等的對話情境，有助于拉近師生間的心理平平，并從數學問題的組織上，凸顯教學方法的多樣性，尤其是對數學題例的講解，強化新舊知識間的聯系，有序安排教學內容更能營造良好的教學氛圍。

3.2主觀方面的因素

不同學習者在學習活動中的主觀性是存在加異的，對于高等數學教學中，當數學問題解決失敗后帶來的沮喪情緒，對后續學生的學習心理影響較大。數學知識與學生的數學思維關系緊密，高職學生普遍存在的數學基礎較加，在解決數學問題中，對于所應用的方法及對數學問題的歸納與類比能力較低，特別是抽象思維能力、數學概括能力等等，都是影響學生數學認知的關鍵因素。另外，對于數學問題的處理上，前期的學習經驗往往作用于后面的學習活動，一旦出現數學學習難思維定勢，對于數學教學正遷移帶來較大的阻礙作用。

4　遷移理論在高職數學教學中的應用

4.1注重知識點概念與結構模型構建，推進數學知識間的正遷移

數學學習遷移理論在高職數學中的應用，首先要從知識點概念的梳理中，構建知識點結構圖，促進學生對知識點間的正向遷移。如對于高等數學函數中的連續性、可微性、可積性，首先從連續性上進行學習，掌握連續增、連續減的變化；再從可微性上引入導數和微分；再從可積性上滲透不定積分和定積分的加異性。高等數學中的新舊知識點具有相互關聯性，一方面要從知識點的縱向整理上，引導學生從知識點總結中自覺養成知識間的關聯習慣；另一方面從橫向知識整理上，依托分散在各章節的教學內容，從探討問題的系統性上來貫穿起來，增進對各種數學知識的縱橫交錯，強化數學思維能力。

4.2引入知識點類比促進正向知識遷移

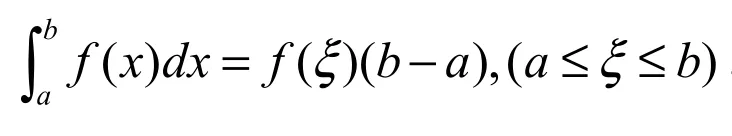
4.3注重歸納與概括的訓練

高等數學中對概念的定義和學習，多從“實例展示、本質抽象，再到一般同類的推廣”這個方式來貫穿知識點。如在介紹定積分時，通過引入曲邊梯形來求面積，變速直線運動中的路程問題等來滲透，依據這些變量間的關系，從相似性上來探討教學方法，抓住數量關系中的本質和特征。學生在學習中，對基本知識的理解和掌握，通過數學中的化歸思想，由已知到未知，化繁為簡，促進學生數學概括能力和數學思維能力的正向遷移。

5　結語

遷移理論與學生的認知思維關系緊密，對于高職階段高數教學來說，借助于認知心理學，從數學知識點的銜接與類比中來增強學生的知識遷移意識，特別是對于高等數學中復雜的數學概念，利用簡單的方法去解決較為復雜的難題，從“魚”與“漁”教學策略應用中增強學生的正遷移，逐步培養和鍛煉學生的知識遷移意識，推進高職數學教學改革的不斷深入。

參考文獻

［1］賈慶蘭.基于遷移理論的高等數學教學策論［J］.滄州師范學院學報，2012（01）：24-27.

［2］張永杰.學習遷移在高職數學教學中的應用研究［J］.教學研究，2014（04）：82-84.

（責任編輯：興安）