基于彈塑性有限元方法的轉盤軸承材料許用接觸應力研究

鄭紅梅，田貴，梁昌文，鄭巖，李庚袁

(合肥工業大學 機械與汽車工程學院，合肥 230009)

轉盤軸承承受的工作載荷大而接觸面小，應力集中明顯，滾道的損壞是其主要失效形式，因此材料應具有良好的力學性能[1-2]和較高的耐磨性[3]，且能承受較高的接觸應力。對于轉盤球軸承，工作中溝道可承受高達4 000 MPa以上的交變接觸應力。GB/T 4662—2012《滾動軸承 額定靜載荷》規定了優質淬硬鋼球軸承的許用接觸應力為4 200 MPa，其相關參數是基于Hertz理論點接觸公式計算的。對于套圈材料為42CrMo和50Mn的非淬透性鋼制大型轉盤軸承，還沒有規定其最大接觸應力，因此有必要對其許用接觸應力進行測定。文獻[4-5]進行了轉盤軸承許用接觸應力的試驗研究，根據試驗所獲數據，通過Hertz理論計算得到接觸應力，對接觸應力和對應的壓坑深度采用回歸分析，測得材料的許用接觸應力。

決定轉盤軸承材料性能的關鍵是熱處理工藝[6]，加工時要對工藝準確把握。許用接觸應力測定試驗的關鍵是壓痕深度的測量，由于轉盤軸承材料良好的力學性能，壓痕一般較小，測量需要借助高精度儀器。

以轉盤軸承材料50Mn為研究對象，對其進行平板與鋼球對壓研究，從彈塑性有限元角度分析得到壓痕深度，結合文獻[4-5]處理接觸應力和壓痕深度方法，對彈塑性有限元分析的數據進行處理，代替試驗測得材料的許用接觸應力。

1 彈塑性有限元法

許用接觸應力測定試驗主要測定卸載后永久壓痕深度，利用彈塑性有限元方法得到簡化模型，通過分析模型得到試驗對應的數據。

轉盤軸承材料表面經過感應淬火，表層會出現明顯的硬化，壓縮屈服強度大大提高，在建立彈塑性有限元模型時需要考慮滾道材料的塑性[7]。為了獲得塑性數據，根據GB/T 7314—2005《金屬材料 室溫壓縮試驗方法》進行了材料的室溫壓縮試驗，得到表面硬度為57 HRC的轉盤軸承材料50Mn的塑性數據，即應力應變關系，見表1。

表1 50Mn材料塑性數據

1.1 彈塑性有限元模型

以平板試樣與鋼球對壓為原型，考慮到模型的對稱性，建立1/4模型，如圖1所示。基于六面體單元的計算精度和網格數量優于四面體單元[8]，全部采用六面體網格，在接觸處局部細化網格并加載。

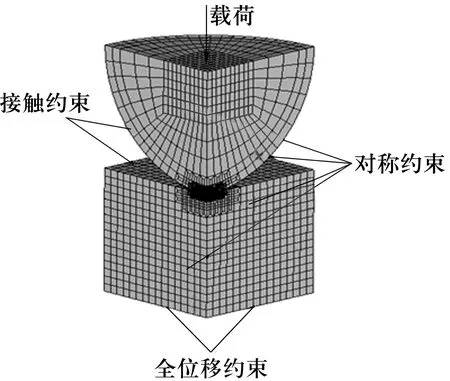
圖1 滾球壓平板邊界條件與載荷加載示意圖

網格模型單元數為60 338，節點數為65 133。鋼球半徑為10 mm，50Mn材料的彈性模量為2.1×105MPa，泊松比為0.3。

1.2 彈塑性有限元分析得到壓痕深度

采用ABAQUS軟件分析，定義材料屬性時將表1數據寫入塑性中，分析時彈性和塑性因素全部考慮。施加載荷，卸載后的等效應力分布如圖2所示，塑性變形如圖3所示，最大Hertz接觸應力和壓痕深度見表2。由圖可知，最大位移出現在鋼球和平板接觸中心處，應力分布和壓痕的形狀都與實際相符，可以準確讀出壓痕深度。

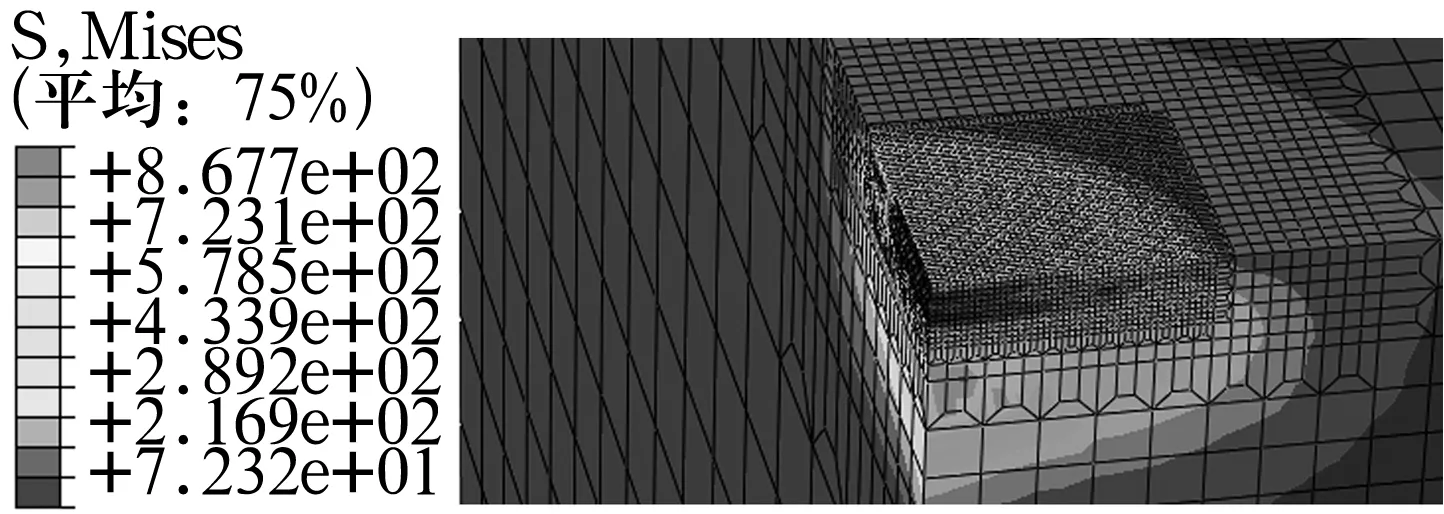
圖2 等效應力云圖

圖3 等效塑性應變圖

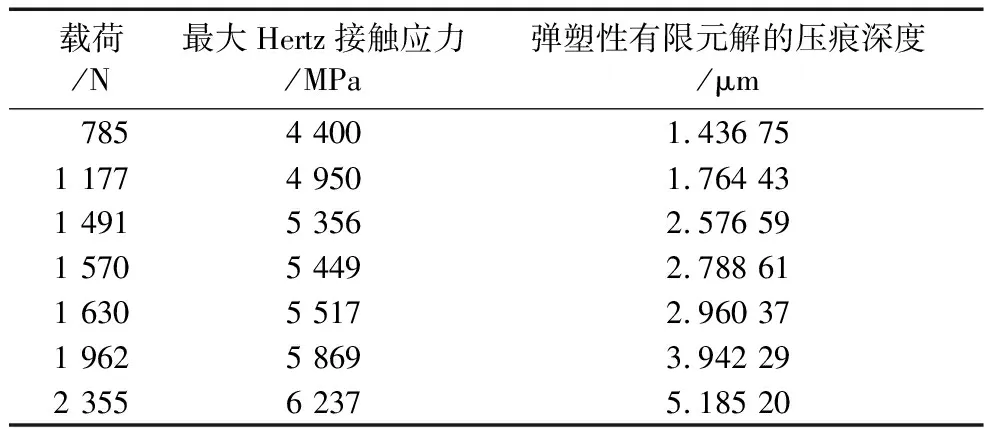
表2 不同載荷下的最大接觸應力和壓痕深度

2 試驗法測量壓痕深度

使用中頻淬火加工試樣(200 mm×50 mm×60 mm)，保證與室溫壓縮試驗試樣的力學性能相同(表面硬度57 HRC)。

利用電子萬能材料試驗機(WDW-100)對試樣進行多次緩慢加載，加載范圍500～5 000 N，達到一定載荷穩定一段時間后卸載，試驗裝置如圖4所示，壓頭夾持裝置上GCr15鋼球的直徑為10 mm。

1—壓力機上砧座；2—墊塊；3—壓頭；4—平板試樣；5—壓力機下砧座

用輪廓儀測量不同載荷下試樣表面冠狀壓痕深度，部分結果見表3。

表3 試驗數據

3 對比分析

3.1 數據處理

3.1.1 彈塑性有限元方法數據

根據Hertz理論，球與平板對壓的最大接觸應力為[6]

(1)

式中:P為載荷；E為材料彈性模量；ν為材料泊松比；∑ρ為綜合曲率，∑ρ=0.4；μ，w為應力分布系數，球與平板接觸情況下μ=w=1。

許用接觸應力測定試驗采用線性回歸法分析接觸應力和壓痕深度。壓痕深度δq與鋼球直徑Dw之比δq/Dw和最大接觸應力σmax的關系為[4-5]

(2)

式中：K為常數；b為指數。

y=a+bx，

(3)

相關系數r為

(4)

將表2的接觸應力和壓痕深度代入上述公式，即采用回歸分析法可得到：a=-17.532 30，b=3.758 226，r=0.942 284。

還原方程得到接觸永久變形與鋼球直徑之比對接觸應力的關系方程為

(5)

由于在試驗中很難找到準確的彈性變形到塑性變形的臨界點，工程上一般以產生0.03%(或0.01%，0.05%)殘余變形的應力作為彈性極限[6]。文獻[9]認為當轉盤軸承滾道的永久變形量為滾子直徑的0.03%時，不會影響轉盤軸承運轉的平穩性和壽命。因此設定溝道塑性變量為鋼球直徑0.03%時的應力為材料的許用接觸應力，故將δq/Dw=0.03%代入(5)式，求得許用接觸應力為5 342 MPa。

3.1.2 試驗數據

同樣用回歸分析法處理試驗數據，用MATLAB軟件進行擬合，擬合曲線如圖5所示。

圖5 試驗數據擬合曲線

根據擬合結果，求得相關系數r=0.964 514，說明σmax與δq/Dw相關。擬合曲線方程為

(6)

由上式求得許用接觸應力為5 517 MPa，即永久變形量為鋼球直徑0.03%時的接觸應力，對應的加載載荷為1 630 N。

3.2 結果對比

試驗得到的許用接觸應力和彈塑性有限元模型分析得到的許用接觸應力分別為5 517 MPa和5 342 MPa，誤差為3.2%，在工程上是可行的。由于彈塑性有限元計算需要大量時間，文中只計算了部分數據，當彈塑性有限元方法分析的數據更多時誤差會更小。將試驗的壓痕深度和彈塑性有限元分析所得深度進行比較，結果見表4,兩者所得結果相近，除個別明顯不合理的試驗數據，大部分誤差在0.05%左右。若塑性特性曲線更加精確，誤差會更小。因此，建立的彈塑性有限元模型可以用來測定轉盤軸承材料的許用接觸應力。

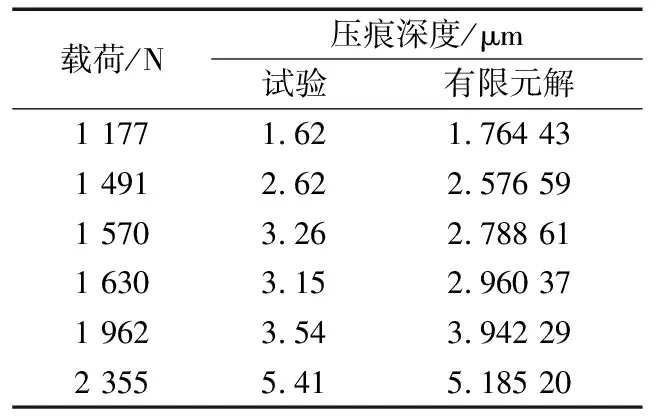
表4 壓痕深度對比

4 結束語

建立了50Mn轉盤軸承材料接觸永久變形與鋼球直徑之比對接觸應力的關系方程，測得了當δq/Dw=0.03%時，轉盤軸承材料50Mn與鋼球對壓試驗的許用接觸應力值，提出了許用接觸應力測定的彈塑性有限元方法，經試驗對比證明，該方法可以替代試驗法用于測定轉盤軸承材料的許用接觸應力。