基于SVD-LCD與1.5維譜的滾動軸承故障診斷
崔偉成, 李偉, 孟凡磊,劉林密
(海軍航空工程學院 飛行器工程系,山東 煙臺 264001)
滾動軸承發生故障時,其振動信號具有故障特征微弱,非平穩、非線性等特征,準確地進行故障診斷較為困難。因此,最大限度的提高測量信號的信噪比,并研究適用于非平穩信號的時頻分析及故障特征提取方法具有重要的工程意義。
奇異值分解( Singular Value Decomposition,SVD) 降噪是一種非線性濾波方法,具有良好的穩定性和不變性,可以有效降低信號中的噪聲,提高信噪比[1-2]。為準確分解信號,得到分量的局部特征,眾多學者開展了時頻分析技術的研究[3-5],并在本征時間尺度分解的基礎上創造性的提出了局部特征尺度分解(Local Characteristic-Scale Decomposition,LCD)[6-8]。LCD在保證分解所得分量物理意義清晰的基礎上,具有計算時間短、端點效應不明顯等優勢,開拓了自適應時頻分析方法的新思路[9]。1.5維譜是一種降維的高階累積量譜,對高斯噪聲不敏感,理論上可以完全抑制高斯噪聲和非高斯的有色噪聲,同時又能保持非線性系統的相位信息[10-13]。
為了準確得到軸承故障振動信號內含的故障特征信息,首先采用SVD降噪技術提高信號的信噪比,然后對降噪信號進行LCD,并將分解后的內稟尺度分量(Intrinsic Scale Components,ISC)進行Hilbert變換求包絡信號,最后應用1.5維譜技術提取故障特征,給出診斷結果。
1 基本理論
1.1 奇異值分解降噪
SVD 降噪的原理基于相空間重構,利用信號與噪聲的能量可分性,對含噪信號構成的矩陣進行分解,僅保留信號特征奇異值,達到去除噪聲目的[1-2]。
1.1.1 嵌入
設原始信號為X=[x1,x2,…,xN],利用相空間重構理論重構的吸引子軌跡矩陣為
,(1)
式中:A為m×n階的Hankel矩陣;τ為延遲步長;n=N-(m-1);m為嵌入維數。
1.1.2 奇異值分解
對(1)式進行其奇異值分解得
(2)
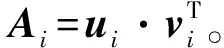
1.1.3 分組
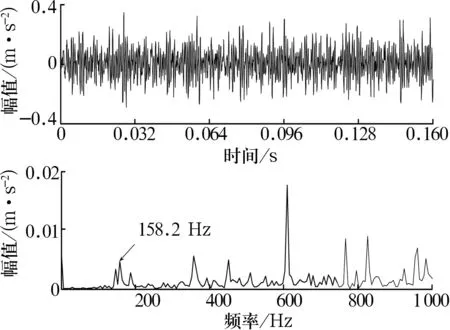
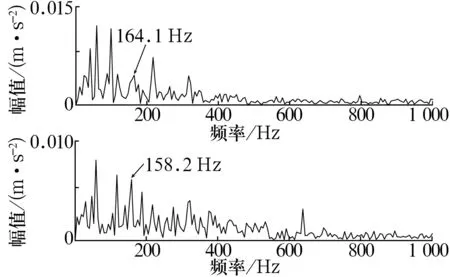
對于分解得到的奇異值,認為前r(r 1.1.4 對角平均化 對角平均化的目的是將上述分組得到的信號矩陣轉化成長度為N的序列,即由信號分量重構信號。 1.2.1 內稟尺度分量 LCD方法假設任何復雜信號均由不同的ISC組成,并且各ISC之間相互獨立。 LCD實質就是將任意信號x(t)分解成若干個ISC之和,從而達到對信號分解的目的。每個ISC必須滿足2個條件: 1)在整個數據段內,任意2個相鄰的極值點符號互異。 2)在整個數據段內,設所有的極值點為Xk,對應的時刻為τk(k= 1,2,…,M;其中M為極值點的個數)。取任意2個相鄰的極大(小)值點(τk,Xk)和(τk+2,Xk+2)可構成τk+1時刻的一個函數值,即 (3) 則Ak+1與其對應的極大(小)值Xk+1的比值關系不變,即 aAk+1+(1-a)Xk+1=0, (4) 式中:a∈(0,1),為一常量,典型地a=0.5。 這2個條件保證了相鄰極值點之間的單調性,即波形的單一性;同時保證了所獲得ISC波形的光滑性和對稱性。從而使每個ISC在任意的極大值和極小值之間具有單一的模態,可以局部地與正弦曲線相吻合,使得瞬時頻率具有了相應的物理意義。 1.2.2 分解過程 根據ISC的定義,對任意實信號x(t)進行LCD的過程為: 1)確定信號x(t)的所有極值點Xk及對應的時刻τk(k= 1,2,…,M)。對2個時間序列進行延拓,延拓方式為兩端各增加一個極值點,即 (5) (6) 延拓后的時間序列分別為Xk,τk(k= 0,1,…,M+1)。 2)設置參數a的值,基線控制點計算式為 Lk+1=aAk+1+(1-a)Xk+1= 3)計算基線信號段 (8) 式中:Hk(t)為對原始信號的第k個區間進行線性變換得到的基線信號段。 4)由Hk(t)依次連接成基線信號H1(t),并將H1(t)從原始信號中分離,即 h1(t)=x(t)-H1(t)。 (9) 若h1(t)是ISC,輸出I1(t)=h1(t)。否則將h1(t)作為原始信號將步驟1~4重復循環k-1次,得到I1(t)=h1k(t)。 5)將I1(t)從信號x(t)中分離,可得新的剩余信號 r1(t)=x(t)-I1(t)。 (10) 6)將r1(t)視為原始數據,將步驟1~5重復循環n-1次,直至rn(t)單調或者為一常數。這樣就將x(t)分解為n個ISC和1個剩余信號之和,即 (11) 1.5維譜定義為3階累積量對角切片的Fourier變換[10]。對于零均值平穩隨機過程x(t),其三階累積量定義為 c3x(τ1,τ2)=E[x(t)x(t+τ1)x(t+τ2)], (12) 式中:E為數學期望;τ1,τ2為不同的時間延遲。 令τ1=τ2=τ,得到三階累積量的主對角切片為 c(τ)=c3x(τ,τ)=E[x(t)x(t+τ)x(t+τ)]。 (13) 對c(τ)進行一維Fourier變換可得x(t)的1.5維譜,即 (14) 由上述定義可看出,1.5 維譜為雙譜在一維頻率空間上的投影。由于零均值高斯噪聲的三階累積量值為零,1.5 維譜相對于雙譜不僅計算量減小,還保留了雙譜對隨機噪聲的抑制作用和非二次相位耦合諧波的剔除能力。 基于SVD-LCD與1.5維譜的滾動軸承故障診斷方法基本流程如圖1所示。首先,結合相空間重構技術構造振動信號的Hankel矩陣,對Hankel矩陣進行SVD降噪,確定奇異值有效階次并將原始信號分成信號分量和噪聲分量,對信號分量重構得到降噪信號;然后,對降噪后的信號進行LCD,得到若干ISC,將分解后的ISC進行Hilbert變換得到包絡信號;最后,求取包絡信號的1.5維譜,進行故障特征提取。 圖1 故障診斷流程圖 SVD降噪的關鍵參數有Hankel矩陣的構造參數及奇異值有效秩階次。 1)Hankel矩陣的構造涉及2個重要參數:延遲步長τ和嵌入維數m,在此選取τ=1,m=N/2[1]。 2)奇異值有效秩階次采用奇異值均值法確定,即將所有低于奇異值平均值的奇異值置零[2]。 1)標準LCD算法采用分段線性方法,由基線控制點計算基線信號。為了得到更光滑的ISC,采用三次樣條方法替代分段線性方法。 2)ISC判據采用標準偏差判據[6-9]。 3)終止條件選用剩余信號能量判據[6-9]。 試驗數據來自美國凱斯西儲大學電氣工程實驗室[14]。試驗軸承為6205-2RS型深溝球軸承,該軸承的尺寸參數見表1。 表1 6205-2RS的尺寸參數 試驗中采用加速度傳感器采集振動信號,采樣頻率fs=12 kHz,采樣點數取N=2 048。使用電火花加工技術在該軸承內圈上布置了單點故障,故障直徑為0.177 8 mm,該軸承用于支承電機軸,電動機轉速為1 772 r/min,計算得軸承內圈點蝕故障特征頻率為159.96 Hz。 原始信號的時域波形和頻譜如圖2所示(為清晰展現故障特征,只給出0~1 000 Hz頻段的頻譜)。從圖中可以看出:時域波形的信號比較雜亂,不易發現周期成分;頻譜上隱約可以看見158.2 Hz處存在譜線,考慮到計算誤差,可近似認為158.2 Hz即為軸承內圈故障特征頻率,但特征很不明顯。 圖2 原始信號的時域波形及頻譜 直接對原始采樣信號進行LCD,得到2個ISC分量和1個剩余信號。2個分量的時域波形如圖3所示,從圖中可以看出:2個分量的頻率段沒有明顯差別,分解產生了明顯的模態混疊;而且未發現低頻分量,分解不夠徹底。 圖3 原始信號LCD后的ISC時域波形 應用Hilbert變換求取各ISC的包絡譜,其低頻段如圖4所示。從圖中可以看出:1)分量1在164.1 Hz處存在譜線,但不夠突出;2)分量2在158.2 Hz處存在較為清晰的譜線,但不是最大譜峰;3)在2個分量包絡譜中,特征頻率倍頻處未發現明顯的譜線,不易給出是否軸承內圈故障的結論。 圖4 ISC的包絡譜 對原始采樣信號進行SVD降噪處理并進行LCD,得到4個ISC和1個剩余信號。4個ISC的時域波形如圖5所示,從圖中可以看出:LCD類似于自適應的濾波器,4個ISC所包含的頻率段逐漸降低,模態混疊現象得到了明顯的抑制;而且分量4的幅值明顯小于原始信號,從能量的角度來看,分解較為徹底。 圖5 原始信號SVD-LCD后的ISC時域波形 求取各個ISC的Hilbert包絡譜,其低頻部分如圖6所示。從圖中可以看出:1)在分量1的包絡譜中,158.2 Hz處存在較為清晰的譜線,雖不是最大譜峰,但其特征比原始信號LCD的分量1包絡譜明顯;2)在分量2的包絡譜中,158.2 Hz處的譜線存在明顯的譜峰,并且在特征頻率2倍頻(316.4 Hz)處的譜峰也清晰可見;3)在分量3的包絡譜中,158.2 Hz處的譜線是全譜最大峰值,故障特征明顯;4)在分量4的包絡譜中,164.1 Hz處的譜線也相對清晰。將4個譜圖相互印證,可得出內圈故障的結論,與事實吻合。可見,SVD降噪可以降低LCD的模態混疊效應,使分解更徹底,得到的分量更能體現信號的特征,是一種有效的LCD預處理方法。 圖6 原始信號SVD-LCD后的ISC包絡譜 對4個ISC的包絡信號取1.5維譜,其低頻部分如圖7所示。從圖中可以看出:1)在分量2的1.5維譜中的158.2和319.3 Hz處,以及分量3的1.5維譜中的161.1 Hz處均存在清晰譜峰,并且比包絡譜清晰;2)分量4的1.5維譜中,164.1 Hz譜線是全譜最大峰值;3)1.5維譜的噪聲能量遠遠小于包絡譜;4)1.5維譜的計算過程中會引入誤差,可能會使特征頻率及其倍頻發生偏移,在使用時要引起注意。 因此,包絡譜體現的故障特征均可由1.5維譜體現,并且1.5維譜體現的故障特征更明顯,抗噪能力更強。可見1.5維譜是一種有效的LCD后處理方法。 圖7 原始信號SVD-LCD后ISC的1.5維譜 以局部特征尺度分解為基礎,考慮噪聲的影響,提出了一種新的滾動軸承故障診斷方法。該方法通過奇異值分解降噪預處理,提高LCD的質量和準確性,通過1.5維譜后處理,進一步抑制噪聲,突出故障特征。以滾動軸承內圈點蝕故障振動信號為對象,驗證了該方法提取故障信號的有效性,該方法也可推廣至齒輪等旋轉機械故障診斷領域,具有一定的工程應用價值。1.2 局部特征尺度分解
1.3 1.5維譜

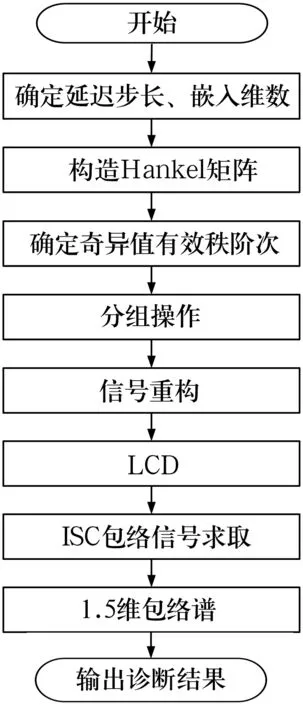
2 基于SVD-LCD與1.5維譜的滾動軸承故障診斷
2.1 SVD降噪參數
2.2 LCD算法
3 試驗分析





4 結束語

