探究高中物理常用三角函數及余弦定理模型
王松志(重慶市璧山縣來鳳中學,重慶 402763)
?
探究高中物理常用三角函數及余弦定理模型
王松志
(重慶市璧山縣來鳳中學,重慶402763)
摘要:本論文探討了在高中物理教學過程中,針對本校高中學生初中基礎較差的實際情況,結合高考對數學能力的要求,對三角函數、余弦定理的應用做一個初步的總結。大致從三個方面來闡述三角函數及余弦定理在物理中的應用:1、三角函數的基本應用;2、運用三角函數求極值;3、運用三角函數探究物理量的變化情況;4、余弦定理的基本應用。從本文的闡述中,促進大家的交流,解決目前高中物理教學的難題。
關鍵詞:高中物理;三角函數
高中物理對數學的應用模型可以簡單地概括為函數模型、三角模型、圖像模型、不等式模型等。三角及余弦函數普遍應用于解決物理問題。
一、三角函數的基本應用

表1 三角函數基本應用表
例題1如圖1所示,質量為m的小球靜止于斜面與豎直擋板之間,斜面傾角為θ,求小球對擋板和對斜面的壓力大小分別是多少?[2]
解析:小球受到的重力產生的效果是壓緊擋板和使球壓緊斜面,重力的分解如圖2所示。


二、三角函數求物理極值
(一)利用輔助角三角函數公式求物理極值。
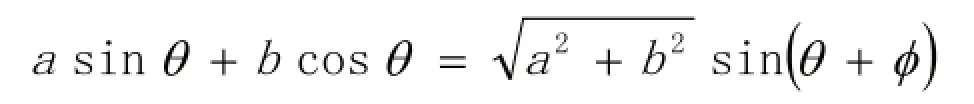
在力學部分求極值或討論物理量的變化規(guī)律時,這兩個公式經常用到。所求物理量的表達式為我們可以通過和差角公式轉化為
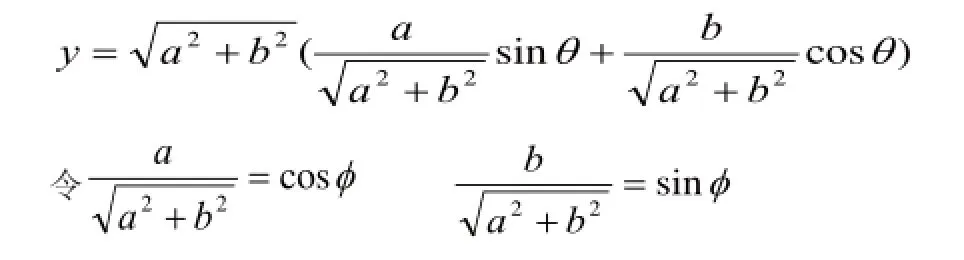
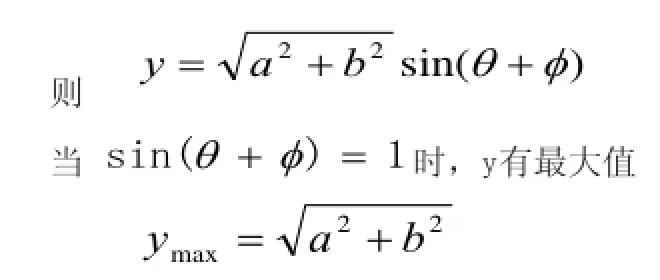
例題2如圖3所示,某同學在地面上拉著一個質量為m=30kg的箱子勻速前進,已知箱與地面間的動摩擦因數為μ=0.5,拉力F1與地面水平夾角為θ=45°.g=10m/s2,求:
(1)繩子的拉力F大小;
(2)該同學能否用比F小的力拉著箱子勻速前進?如果能,請求出拉力的最小值,若不能,請說明理由.[4]
解析:(1)箱子勻速前進,屬于平衡狀態(tài),合外力為零.以箱子為研究對象,進行受力分析,其受重力、地面支持力、地面摩擦力、外界拉力,以水平、豎直方向為坐標軸的方向建立坐標系,利用正交分解法可得

圖3
(2)設拉力與水平方向的夾角為θ,利用正交分解法,將水平、豎直兩個方向的平衡方程整理有
三、利用三角函數求物理量變化情況
利用三角函數探究物理量變化情況常出現在力學中的動態(tài)平衡問題上。這一類問題有兩種方法解決:一是圖解法,二是解析法即找出自變量與因變量之間的函數關系來解答。(例題略)
小結
物理試題的求解過程就是一個將物理問題轉化為數學問題經過求解還原為物理結論的過程。因此在進行高考物理復習的同時,要特別注意數學模型在物理問題中的應用。
中圖分類號:G633
文獻標識碼:A
文章編號:1671-864X(2016)07-0257-01
作者簡介:王松志(1986-),男,重慶人,本科,研究方向為物理教育。

