基于范氏氣體的調諧陣列優化設計
楊云磊, 邱本花, 姚青華
(鄭州科技學院 基礎教學部,鄭州 450064)
?
基于范氏氣體的調諧陣列優化設計
楊云磊, 邱本花, 姚青華
(鄭州科技學院基礎教學部,鄭州450064)
摘要:把范氏氣體條件下的單槍壓力子波模型推廣到調諧氣槍陣列中,研究了3槍調諧氣槍陣列的優化模型及算法,通過數值模擬得出平面陣列作為實驗陣列,運用正交優化設計實驗得出較好的陣列設計方案,為多槍、多子陣陣列優化設計提供參考。
關鍵詞:3槍陣列; 正交實驗; 優化設計; 數值模擬
0引言
隨著地震勘探[1]技術的發展,探測水域的地質結構較為復雜,對氣槍陣列組合子波參數的要求很高,實際操作十分困難[2-3]。因此,作者對獲取壓力子波品質較好的陣列組合進行了深入研究,通過正交實驗選取試驗點進行數值模擬,優化設計氣槍組合,分析陣列類型、氣槍排列方式對子波的影響。
在氣槍陣列的研究中,主要有Safar[4]研究了相鄰氣泡之間相互影響的距離;Nooteboom[5]通過分析避免氣泡之間相互影響的最小槍距,提供了臨界距離的經驗公式;Brandsaeter[6]設計出了能探測深部區域的高分辨率氣槍陣列。針對氣槍組合主要有調諧陣列和相干陣列,通過建立模型、數值模擬得到不同陣列與實測子波的誤差;氣槍陣列設計的研究,現階段主要有王建花等[7]提出的適應深水區地震勘探要求的立體陣列組合和交錯排列氣槍組合;李緒宣等[8]進一步提出立體多陣列和將大容量氣槍放置在中間位置交錯排列的兩種品質較好的陣列設計。
作者在立體陣列組合和交錯排列大容量氣槍組合的基礎上,建立了3槍調諧陣列優化的數學模型,利用正交實驗的方法選取多因素多水平試驗的試驗點,通過數值模擬,得出模擬子波品質較好的三種陣列組合參數設計,為多槍、多子陣氣槍組合參數設計提供參考。
1調諧陣列優化模型及求解
1.1模型建立
建立3槍調諧陣列的優化模型時,要考慮的問題主要有:槍與槍之間的距離;槍的數目;每支單槍的參數,如沉放深度、容量和工作壓力。
1.1.1模型假設
只考慮調諧陣列,對影響壓力子波的參數只考慮工作壓力、容量、沉放深度和槍距,陣列由3槍組成。
模型中陣列中第i支氣槍工作壓力Pi(i=1,2,3),陣列中第i支氣槍容量Vi(i=1,2,3),陣列中第i支氣槍深度Di(i=1,2,3),陣列中槍與槍之間的距離L,考慮的指標參數fi(i=1,2,3,4)。
壓力脈沖峰峰值:
f1(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)=
K1(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)/K1
氣泡脈沖峰峰值:
f2(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)=
K2(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)/K2
初泡比:
f3(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)=
K3(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)/K3
氣泡周期:
f4(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)=
K4(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)/K4
其中:K1為壓力脈沖峰峰值的理論值;K2為氣泡脈沖峰峰值的理論值;K3為初泡比的理論值;K4為氣泡周期的理論值。
1.1.2約束條件
1)調諧陣列中,給出氣槍陣列的一組參數變量指標Pi、Vi、Di(i=1,2,3),有Pig=Pi,Vig=Vi,Pi0=ρgDi。Pig表示第i支氣槍的工作壓力,Vig表示第i支氣槍的初始氣體容量,Pi0表示第i支氣槍沉放位置處靜水壓力;陣列中第i支氣槍的壓力子波Pi(t)可以通過基于范氏氣體的單槍壓力子波模型[9]求解:
(1)
(2)
(3)
(5)
2)給定變量指標L(L表示槍與槍之間的距離),當L取值滿足使得槍與槍之間彼此不受影響時,陣列的壓力子波P(t)就可以通過調諧陣列壓力子波模型求解:
(6)
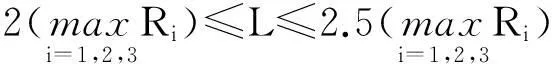
對于固定的陣列組合,對應一組指標fi(i=1,2,3,4),其中:
K1(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)
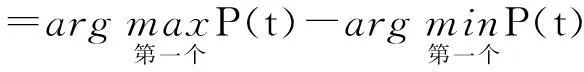
K2(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)
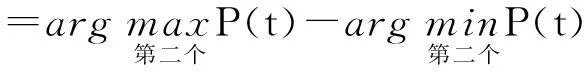
K3(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)
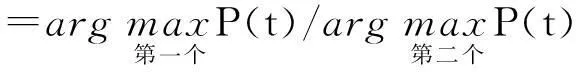
K4(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)
=t3-t1
1.1.3優化模型
目標函數:
maxF(P1,P2,P3,V1,V2,V3,D1,D2,D3,L)
使得
1.2模型求解
1)通過數值模擬比較平面陣列與立體陣列子波參數,選擇平面陣列進行實驗。
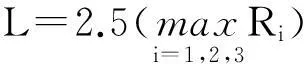
3)通過優化模型進行數值模擬。在對壓力子波參數進行歸一化處理時,由于陣列壓力子波參數沒有一般經驗公式,根據地震勘探對子波參數的要求,選擇:
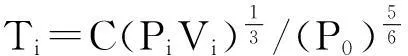
2優化實驗
2.1陣列類型優化實驗
3槍單子陣列實驗時,選擇3支氣槍的容量有大有小,容量較大的槍排在兩個容量較小的槍之間,3支槍在一條直線上,總容量430in3,槍與槍之間的關系為調諧,選擇3 000 psi作為陣列的工作壓力。表1和表2表示兩種情況下陣列中各槍參數設置。
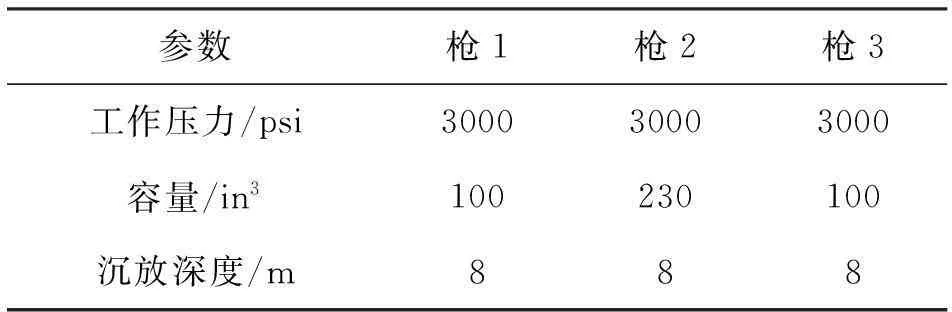
表1 方案一各槍參數選擇
表2方案二各槍參數選擇
Tab.2Parameters of each gun in the second case
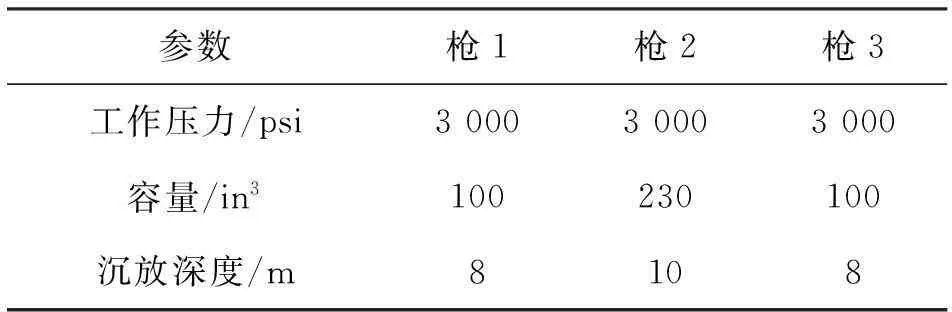
參數槍1槍2槍3工作壓力/psi300030003000容量/in3100230100沉放深度/m8108
表1所示的第一種情況,陣列類型為平面陣列,表2所示的第二種情況,陣列類型為立體陣列。過數值模擬,得出兩種情況下陣列壓力子波及頻譜見圖1~圖4。
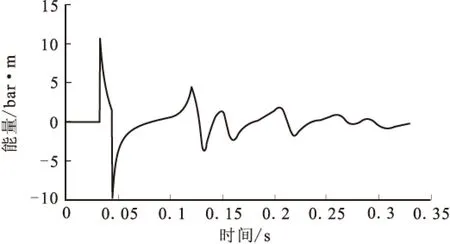
圖1 方案一壓力子波圖Fig.1 Results of the signature in the first case
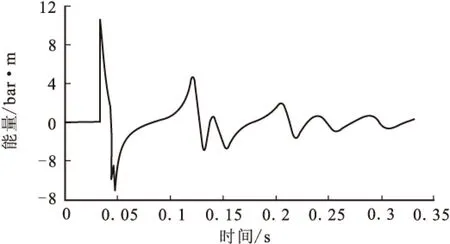
圖2 方案二壓力子波圖Fig.2 Results of the signature in the second case

圖3 方案一壓力子波頻譜圖Fig.3 Wavelet spectrum in the first case
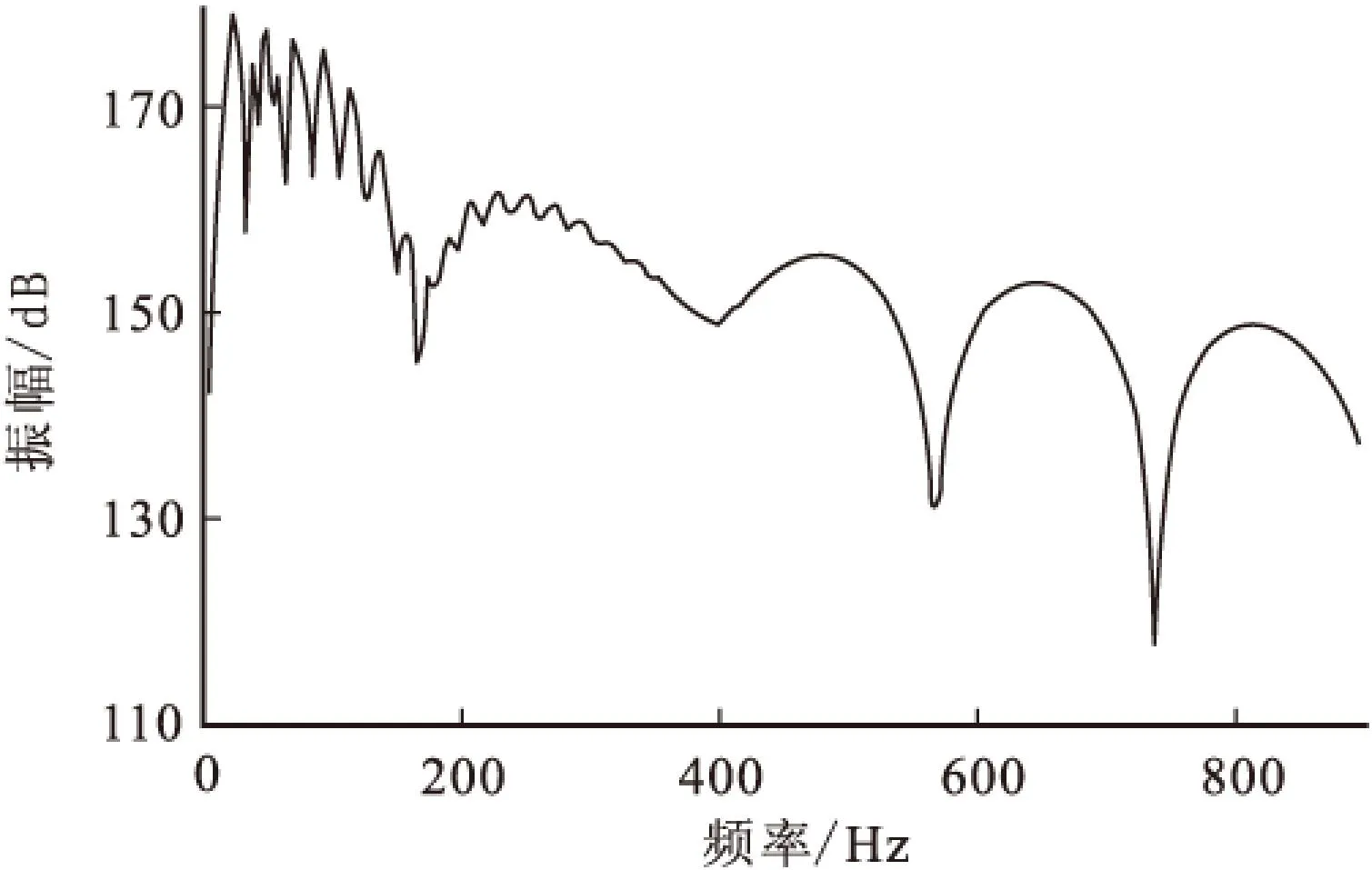
圖4 方案二壓力子波頻譜圖Fig.4 Wavelet spectrum in the second case
通過表3不同方案子波指標對比結果發現,平面陣列輸出能量較高,目標函數值較大,選擇平面陣列進行優化設計。

表3 不同方案子波指標對比
2.2正交優化實驗
在平面陣列的基礎上,選擇氣槍沉放深度為8m,槍距2.5倍最大氣泡半徑。選擇氣槍容量和工作壓力作為試驗因素(表4),對3槍單子陣列進行正交試驗,獲得使得目標函數值最大的陣列設計方案。
在3槍單子陣列優選試驗中,用C表示陣列中的單槍,有C1、C2、C3三個水平,全部試驗方案如表5所示。
由表5中全面試驗方案可知,陣列中每支單槍有4個水平,把每支單槍看作一個因素,這是一個3因素4水平的正交試驗,全面實驗需要進行64次試驗。根據正交試驗設計的代表性和綜合可比性,選擇部分試驗代替全部試驗,這里選擇16個試驗點(表6),進一步選出最優設計方案。
其中:用1表示A1B1;用2表示A1B2;用3表示A2B1;用4表示A2B2。
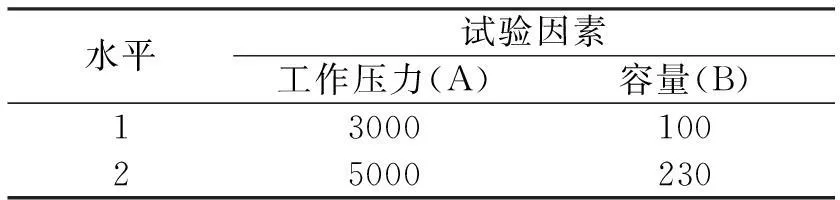
表4 試驗因素水平表

表5 全面試驗方案
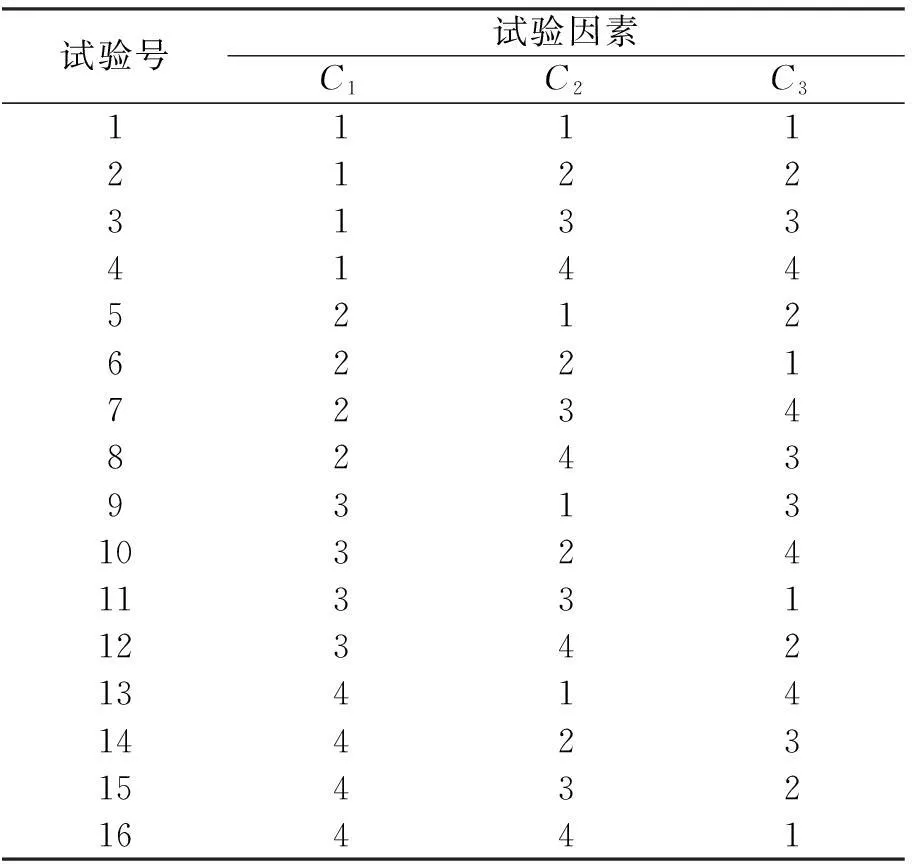
表6 優選試驗點
根據表6中的試驗點,通過優化模型對陣列壓力子波進行數值模擬和頻譜分析,得出每個試驗點的子波指標和第一個陷波點頻率,試驗結果如表7所示。
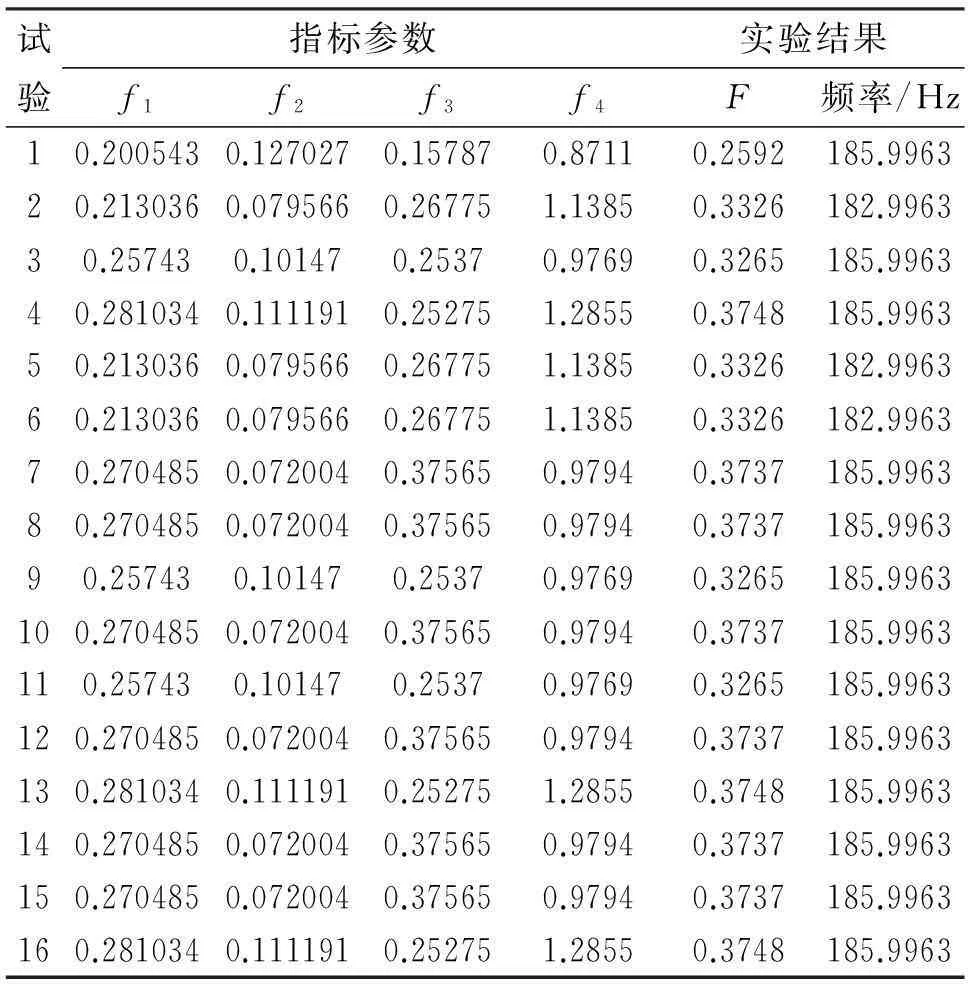
表7 試驗結果
從表7中的實驗結果來看,使得目標函數值最優、第一個陷波點頻率較大的試驗號是4、13、16。這三次試驗槍陣設計如表8所示,圖5和圖6表示試驗號4的壓力子波圖及子波頻譜圖。
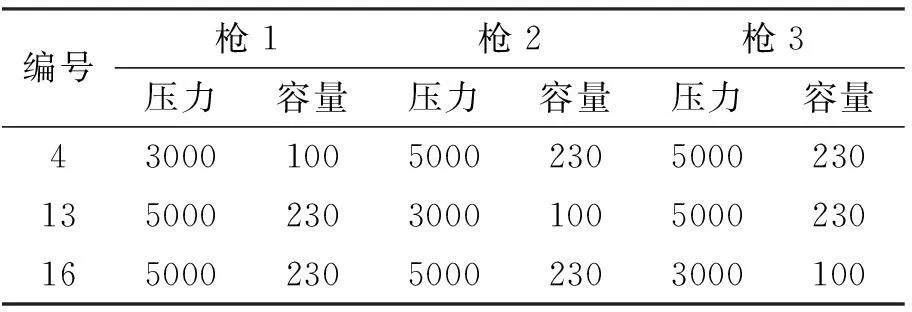
表8 優化的設計方案
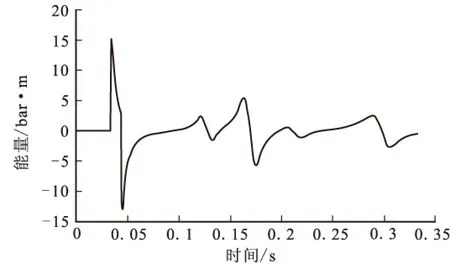
圖5 實驗編號4壓力子波圖Fig.5 Signature of the fourth experiment
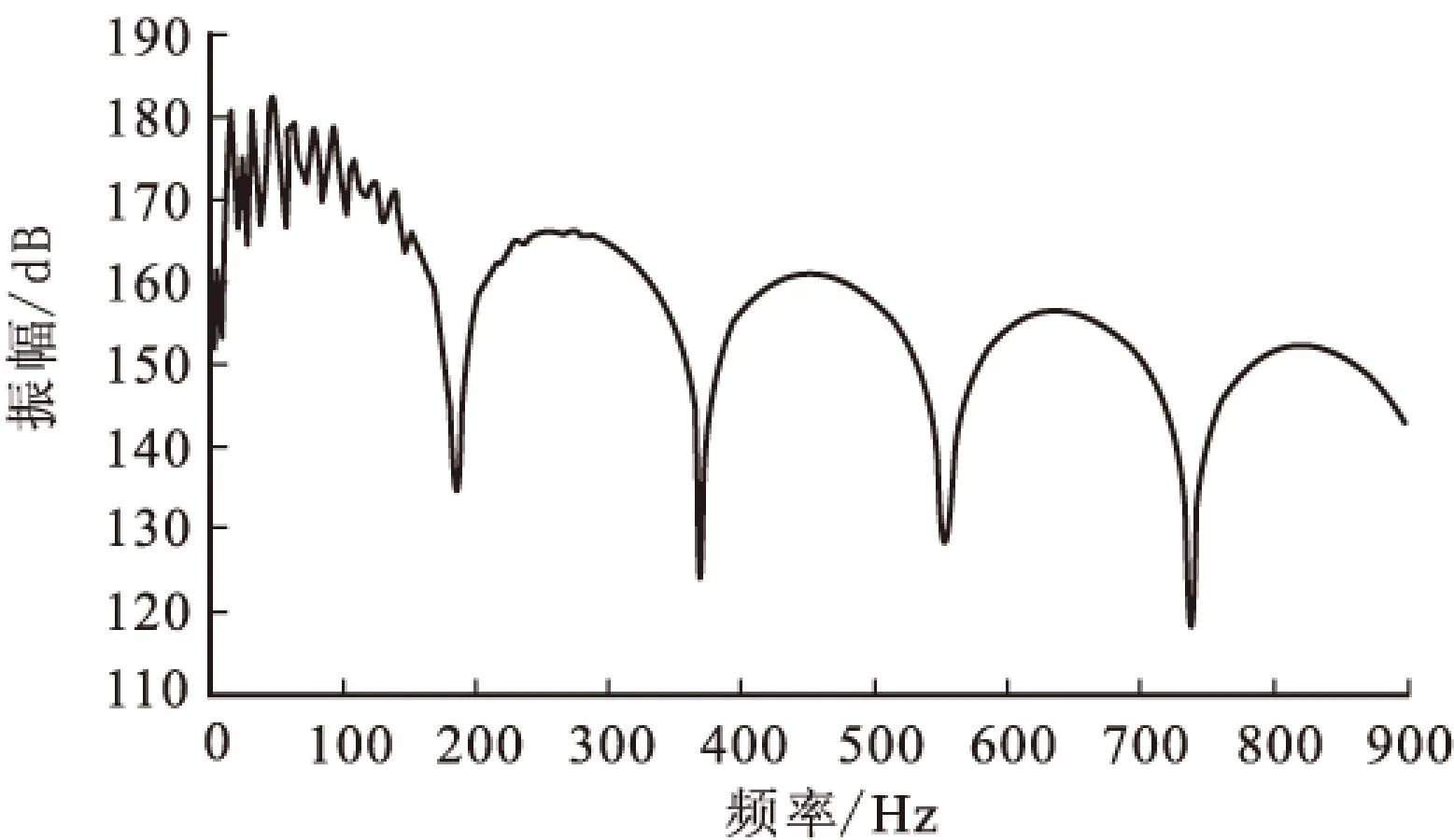
圖6 實驗編號4壓力子波頻譜圖Fig.6 Wavelet spectrum of the fourth experiment
通過表8優化的陣列設計方案表明,在槍陣設計實驗中,通過正交實驗的方法對3因素4水平的槍陣設計進行優化組合,可以選出優化的陣列設計方案,實驗結果具有科學性。因此,可以把通過正交實驗的方法選擇出來的陣列組合設計作為優化的槍陣組合方案,為實際測量槍陣設計提供方法。
3結束語
本次研究主要是在基于范氏氣體的氣槍調諧陣列子波模擬基礎上,建立調諧氣槍陣列的優化模型并給出了模型的求解。由于模型的特殊性,不能通過數值計算找出模型的最優解,作者采用正交實驗的方法找出模型的優化解。通過實驗表明,采用正交實驗尋求陣列組合的優選方案是可行的,從而為多槍、多子陣列設計氣槍參數選擇提供參考。
參考文獻:
[1]余壽朋.高分辨率地震勘探[M].北京:石油工業出版社,1993.
YU S P. High resolution seismic Exploration[M].Beijing: Petroleum Industry Press, 1993.(In Chinese)
[2]陳浩林,全海燕, 於國平,等.氣槍震源理論與技術綜述(上)[J].物探裝備,2008,18(4):211-217.
CHEN H L, QUAN H Y, YU G P, et al.. Summary
of air-gun source theory and technology(1)[J]. Equipment for Geophysical Prospecting, 2008, 18(4): 211-217.(In Chinese)
[3]陳浩林,全海燕,於國平,等.氣槍震源理論與技術綜述(下)[J].物探裝備,2008,18(5):300-308.
CHEN H L, QUAN H Y, YU G P ,et al.. Summary of air-gun source theory and technology(2)[J]. Equipment for Geophysical Prospecting, 2008,18(5):300-308.(In Chinese)
[4]SAFAR M. H. Efficient design of air-gun arrays[J]. Geophysical Prospecting,1976, 24:773-787.
[5]NOOTEBOOM J. J. Signature and amplitude of linear air-gun-arrays[J].GeophysicalProspecting,1978,26:194-201.
[6]BRANDSAETER H., FARESTVEIT A., URSIN B. A new high-resolution or deep penetration air gun array[J]. Geophysics,1979,44:865-879.
[7]王建花,李緒宣,顧漢明. 海上多子陣立體組合氣槍震源優化設計[J]. 地質科技情報 2012,31(2):133-138.
WANG J H, LI X X, GU H M. The optimal design of 3D air-gun arrays combination in marine seismic explotation[J]. Geological Science and Technology Information.2012,31(2):133-138.(In Chinese)
[8]李緒宣,王建花,張金淼,等. 海上氣槍震源陣列優化組合設計與應用[J].石油學報 2012,33(zl):142-148.
LI X X, WANG J H, ZHANG J M ,et al. Design and application of air-gun arrys in marine seismic exploration[J]. ACTA PETROLEI SINICA,2012,33(zl):142-148.(In Chinese)
[9]張雪陽,袁修貴,朱世華.范氏氣體準靜態開放式系統與氣槍子波模擬[J].物探化探計算技術,2014,37(4):458-461.
ZHANG X Y, YUAN X G,ZHO S H. The open quasistatic thermodynamic system in the condition of Vander Waals gas and simulation of air-gun signature[J]. Computing Techniques for Geophysical and Geochemical Exploration,2014,37(4):458-461.(In Chinese)
收稿日期:2015-04-01改回日期:2015-05-19
基金項目:河南省科技廳科技攻關項目(142102210512);河南省鄭州市科技局軟科學研究計劃項目(20141153)
作者簡介:楊云磊(1988-),女,碩士,主要從事氣槍陣列震源模擬與優化方向的研究,E-mail:2813788080@qq.com。
文章編號:1001-1749(2016)03-0410-05
中圖分類號:P 631.4
文獻標志碼:A
DOI:10.3969/j.issn.1001-1749.2016.03.18
Optimization of the tuned arrays in conditions of Van der Waals Gas
YANG Yun-lei, QIU Ben-hua, YAO Qing-hua
(Department of Basic Teaching, Zhengzhou Institute of Science and Technology,Zhengzou450064,China)
Abstract:Based on the single gun wavelet model of Van der Waals Gas, the theoretical model of tuned air gun arrays is established. On three gun array, and the optimization model and numerical simulation is discussed. By the experiment of the planar array is selected. The best design scheme is found through orthogonal experiment,It can provide a reference for multiple air-gun or multiple sub-array.
Key words:three gun array; orthogonal experiment; optimization; numerical simulation

