中子脈沖信號重構算法研究*

王　銀　賀愛玉

(1.安徽理工大學計算機科學與工程學院　淮南　232001)(2.重慶大學光電工程學院　重慶　404100)

?

中子脈沖信號重構算法研究*

王銀1賀愛玉2

(1.安徽理工大學計算機科學與工程學院淮南232001)(2.重慶大學光電工程學院重慶404100)

摘要論文以中子脈沖數據為研究對象,結合壓縮感知算法,模擬仿真中子實驗數據,分別用匹配追蹤算法和壓縮采樣匹配追蹤算法在Mlaltba上實現對中子脈沖信號重構試驗研究。通過改變測量次數和信號稀疏度并利用信噪比SNR、峰值信噪比PSNR、均方誤差SME、均方根誤差RSME等多個參數對重構信號進行分析和比較,以此探究壓縮感知框架下中子脈沖信號的重構。

關鍵詞壓縮感知; 匹配追蹤; 重構算法; 中子脈沖信號; 質量參數

Class NumberTP301.6

1引言

隨著人類信息技術的高速發展,在日常生活中,我們每天要和大量的信息打交道,同時人們對信息量的需求也在增加。由奈奎斯特采樣定理知道根據傳統的信號處理辦法,只有當采樣頻率大于信號最高頻率的兩倍時我才能完整地保存原始信號所包含的信息,因此在處理信息量非常大,比如數碼照相機等圖像信息時,需要非常高的采樣率,同時又要完成對大量原始信息的壓縮、存儲和傳輸工作。這樣就造成了資源的浪費,比如數碼相機中數據量大但最終獲得的數據只有幾Kb。然而大多數信號是可壓縮的,壓縮感知理論就是在采樣的同時完成對信號的壓縮。壓縮感知理論并不局限于信號的帶寬,更多的是利用和發掘信號的內容和結構特性,突破了傳統采樣定理的約束,實現了在遠低于采樣頻率的條件下精確重構原始信號并減少了對信號處理過程硬件的要求。

本文研究的脈沖中子信號數據量是非常大的,但是信號是可壓縮的。鑒于此,采用壓縮感知[1～5]能夠大大提高測量速率,減少電腦存儲的數據量,降低了采樣工作難度。

2中子脈沖信號與壓縮感知理論

本文研究的脈沖中子信號是來自于核信號高速測量系統[6]。核信號高速測量系統是一種新型的核監控系統,其測量系統的物理模型如圖1所示。

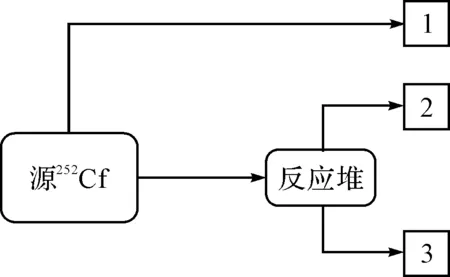
圖1　核信號高速測量系統物理模型

該系統一共有三個通道,252Cf為系統的自發裂變中子源,每自發裂變一次,放射出約四個中子和6個γ射線,它在本系統中起著激發源的作用,也就是系統的驅動中子源。本系統的主要研究對象是堆裂變材料也稱為反應堆。252Cf源產生中子和γ射線后,在堆裂變材料內會產生一系列的裂變中子。第一路為源252Cf快電離室,為被測對象的驅動中子源,并且通過探測器,輸出表示驅動中子源信號。系統所產生的中子脈沖信號在時域內是一串串隨機分布的脈沖,稀疏度相當高,需要經過采集與重構,使得根據這些信息可以對測量系統進行調整分析,如果用傳統采樣方法采集測量到的中子脈沖信號,其計算復雜度和硬件要求是非常高的。

因為核系統是迸發出海量中子信號,傳統的奈奎斯特采樣定理會使得采樣量巨大,而壓縮感知,是通過提取信號特征值來進行數據采集,所以本文通過在Matlab平臺上模擬測量得到的脈沖中子信號,使用壓縮感知理論對信號進行重構是非常有意義的。

3重構算法

3.1MP算法

MP算法[7]作為對信號進行稀疏分解的方法之一,是將信號在完備字典庫上進行分解。假定被表示的信號為y,其長度為n。假定H表示Hilbert空間,在這個空間H里,由一組向量{x1,x2,…,xn}構成字典矩陣D。矩陣D中向量x1,x2,…,xn都可以看為原子(atom),其長度與被表示信號y的長度n相同,同時對這些向量都做歸一化處理,即‖xi‖=1,也就是其單位向量長度為1。MP算法的基本思想是:從完備原子庫即矩陣D中選擇一個與信號y最匹配的原子(也就是其中一組向量xi),構建一個稀疏逼近,并求出信號殘差,然后繼續選擇與信號殘差最匹配的原子,反復進行迭代運算(利用最大相關性準則),最終可以由這些選擇的原子的線性和加上最后的殘差值來表示信號y。當殘差值處在可以忽略的區間內,這些原子的線性組合得到的就是信號y。

接下來分析MP重構算法的缺陷:

max|〈rt-1,θj〉|

(1)

選出與信號殘差最匹配的原子,這里rt-1是信號殘差,θj是矩陣Θ的第j個原子(列向量),t是算法迭代次數,每次迭代后信號殘差可以表示為

rt-1=〈rt-1,θj〉θj+rt

(2)

然后繼續對殘差進行原子匹配,直到滿足迭代停止條件。在MP算法中不能保證新的殘差與已選中的所有原子都正交,如果信號殘差在已選擇的原子進行垂直投影是非正交性的則會使得每次迭代的結果并不是最優的,為使其收斂則需要更多次迭代。

3.2CoSaMP算法

CoSaMP算法[8]是基于正則正交匹配追蹤算法ROMP算法上發展而來,有更高的精確重構理論保證,同時相對于傳統算法匹配追蹤類算法又具有復雜度低的優點,是一種較好的重構算法。但該算法應用時也需要預先知道信號的稀疏度,這一條件則嚴重限制了該算法在很多實際應用方面的實現,算法主要步驟如下:

輸入:原始信號X∈RN,稀疏度K,觀測矩陣Θ∈RM×N,觀測向量y∈RN。

1) 初始化:r0=y、Λ0=[]、t=1。

2) 尋找最匹配的2K個原子的索引J=max{λj=|rt-1,θj|,2K}。

3) 構建候選集C=Λt-1∪J。

4) 求解最小二乘法問題,從C中找出K個最優原子的索引。

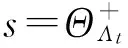
CoSaMP算法流程圖如圖2所示。

圖2　CoSaMP算法流程圖

4基于匹配追蹤類算法重構結果

4.1試驗結果分析

4.1.1CoSaMP算法重構

以Matlab軟件作為試驗平臺,首先在Matlab上模擬脈沖中子信號,然后通過重構程序將信號恢復出來。前面講過要高概率重構原始信號[9],測量次數M需滿足M≥Klog(N/K),所以可以通過改變測量次數和信號稀疏度來探究各種重構方法的重構效果。

1) 信號的稀疏度K=4,測量次數m=100,信號長度n=256。所得到的原始信號及重構信號如圖3所示。

圖3　CoSaMP算法重構

2) 稀疏度K=4,測量次數m=40,信號長度n=256。得到的原始信號與重構信號如圖4所示。

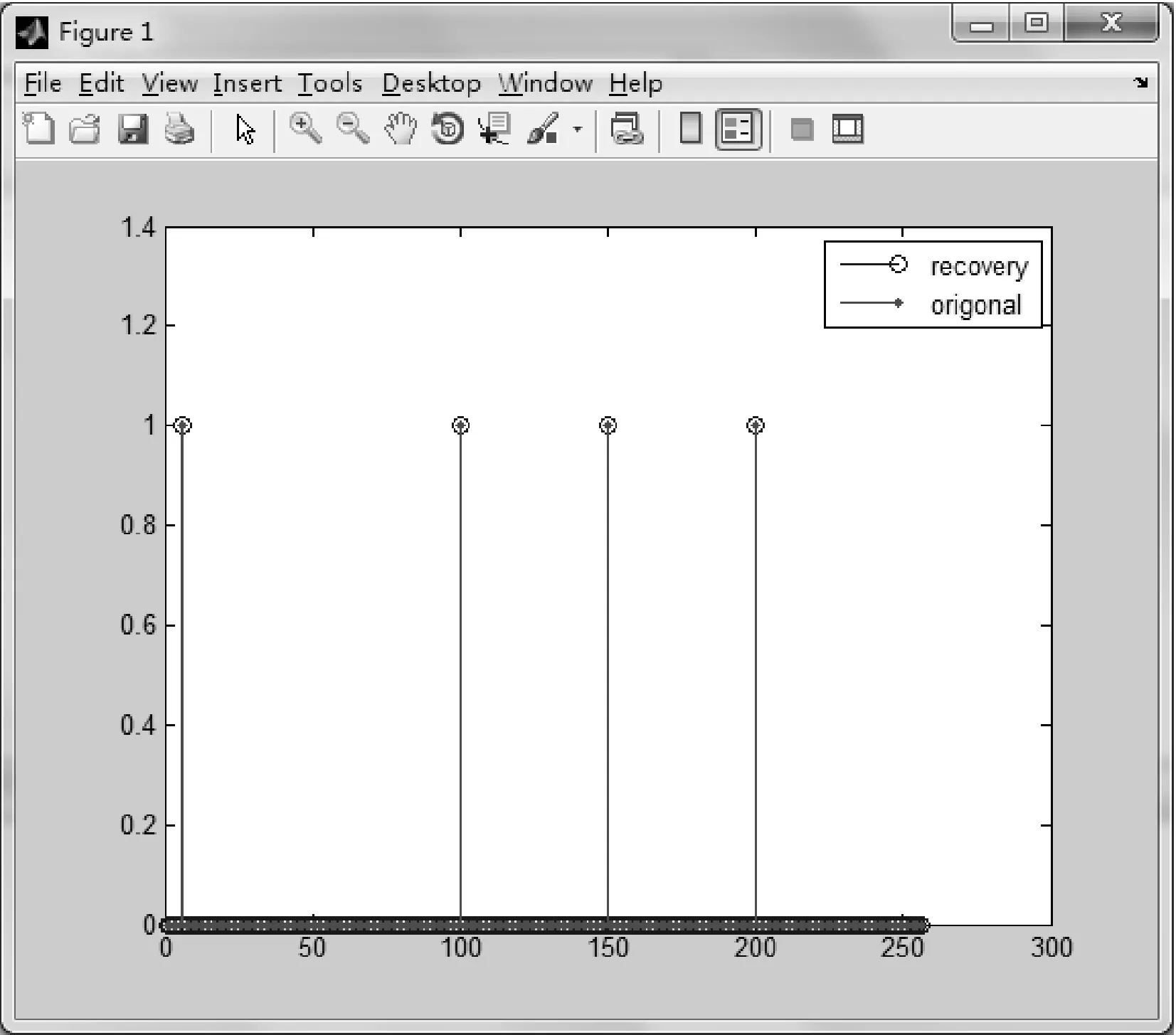
圖4　CoSaMP算法重構

3) 稀疏度K=10,測量次數m=70,信號長度n=1024。原始信號與重構信號對比。

4) 稀疏度K=10,測量次數m=80,信號長度n=1024。試驗結果如圖6所示。

可以看出當稀疏度為4,信號長度為256的時候,測量次數m為40就可以很好重構原始信號。而當信號長度為1024,稀疏度為10,經過多次試驗得出測量次數需達到70才能精確重構原始信號。

圖5　CoSaP算法重構

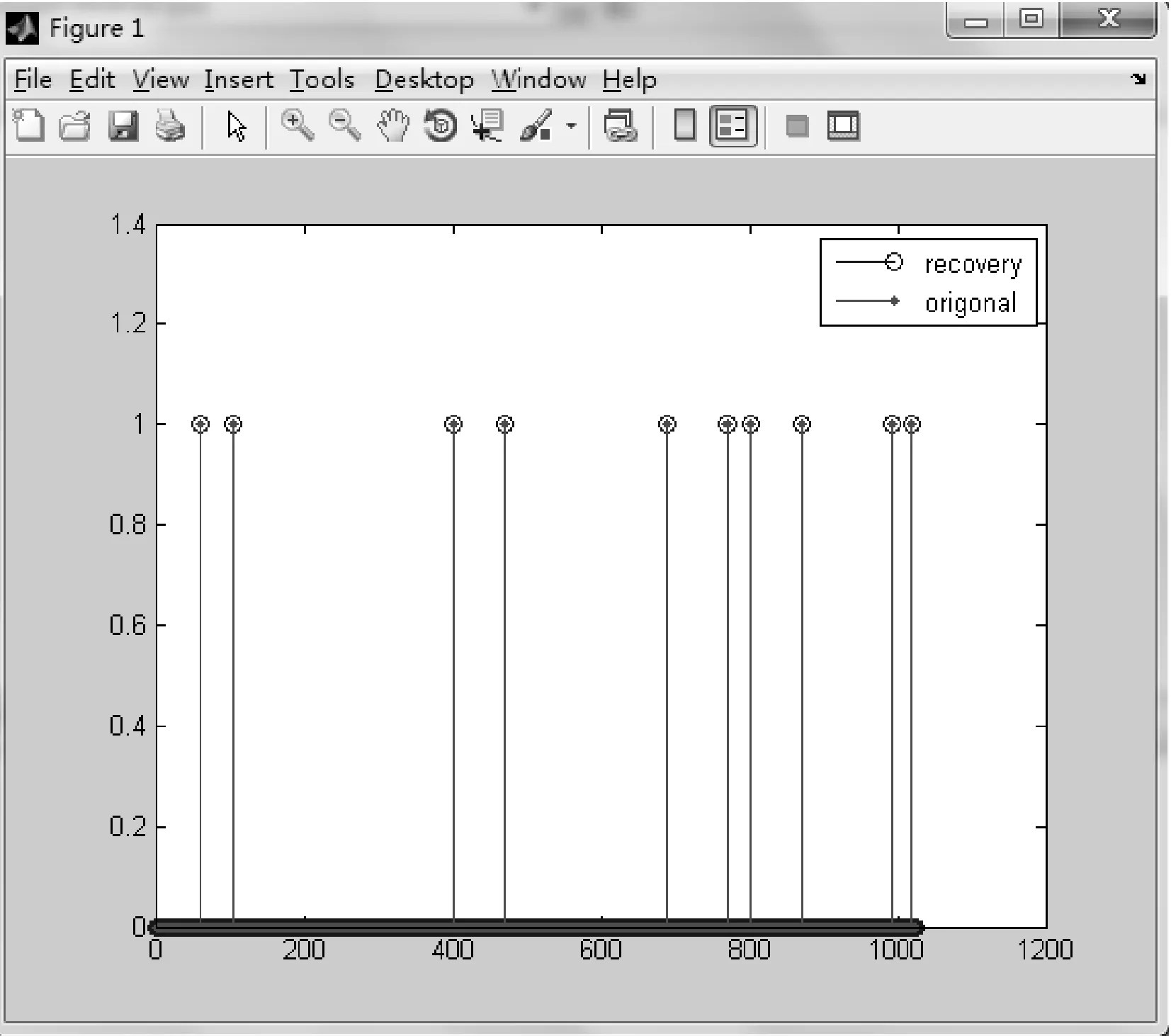
圖6　CoSaMP算法重構

4.1.2MP算法重構

MP算法測量次數m同樣需要滿足M≥Klog(N/K),在相同的稀疏度K與測量次數m條件下,對比CoSaMP重構算法的重構結果。

1) 信號的稀疏度K=4,測量次數m=100,信號長度n=256。所得到的原始信號及重構信號如圖7所示。

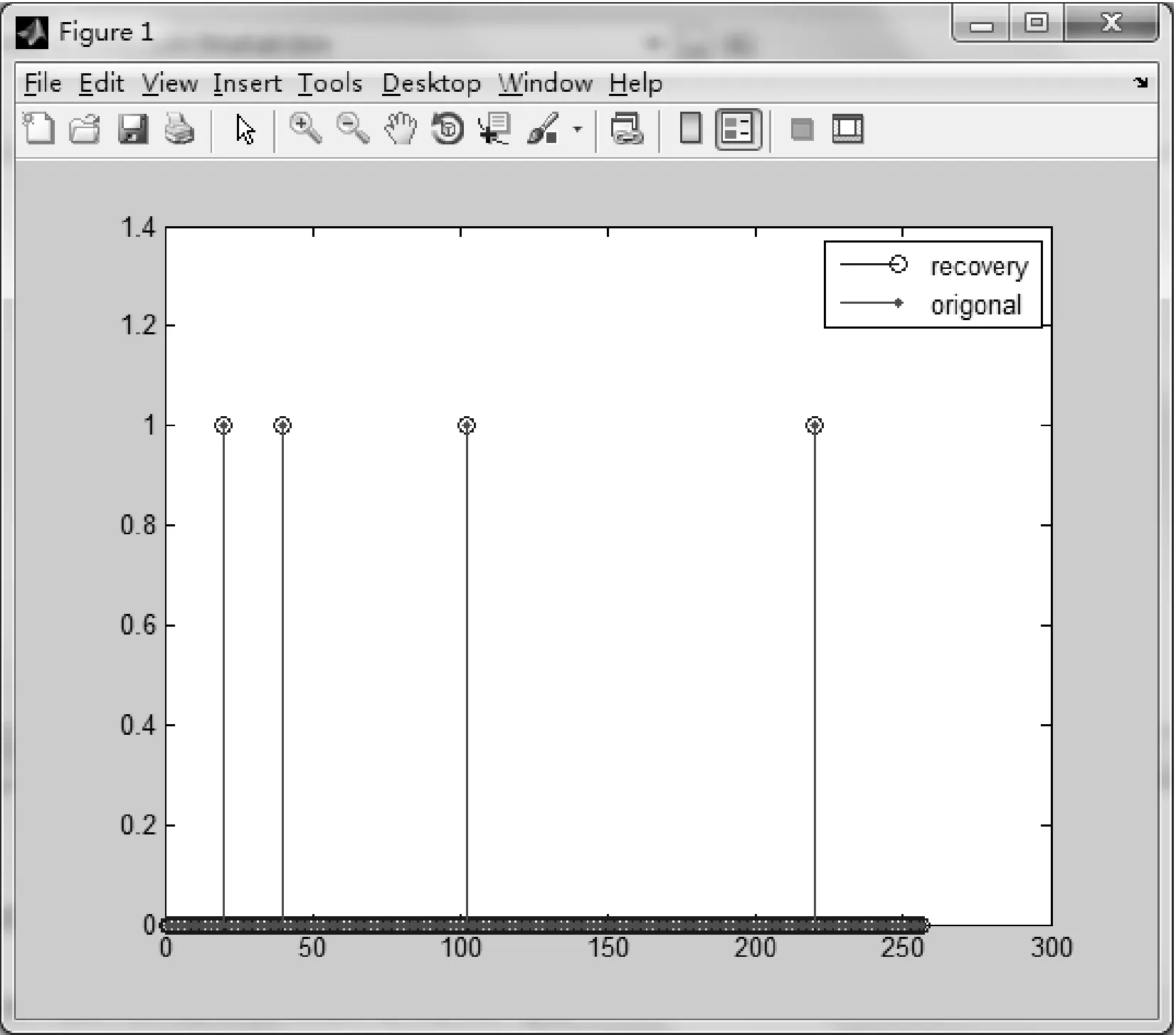
圖7　MP算法重構

2) 稀疏度K=4,測量次數m=40,信號長度n=256。得到的原始信號與重構信號如圖8所示。

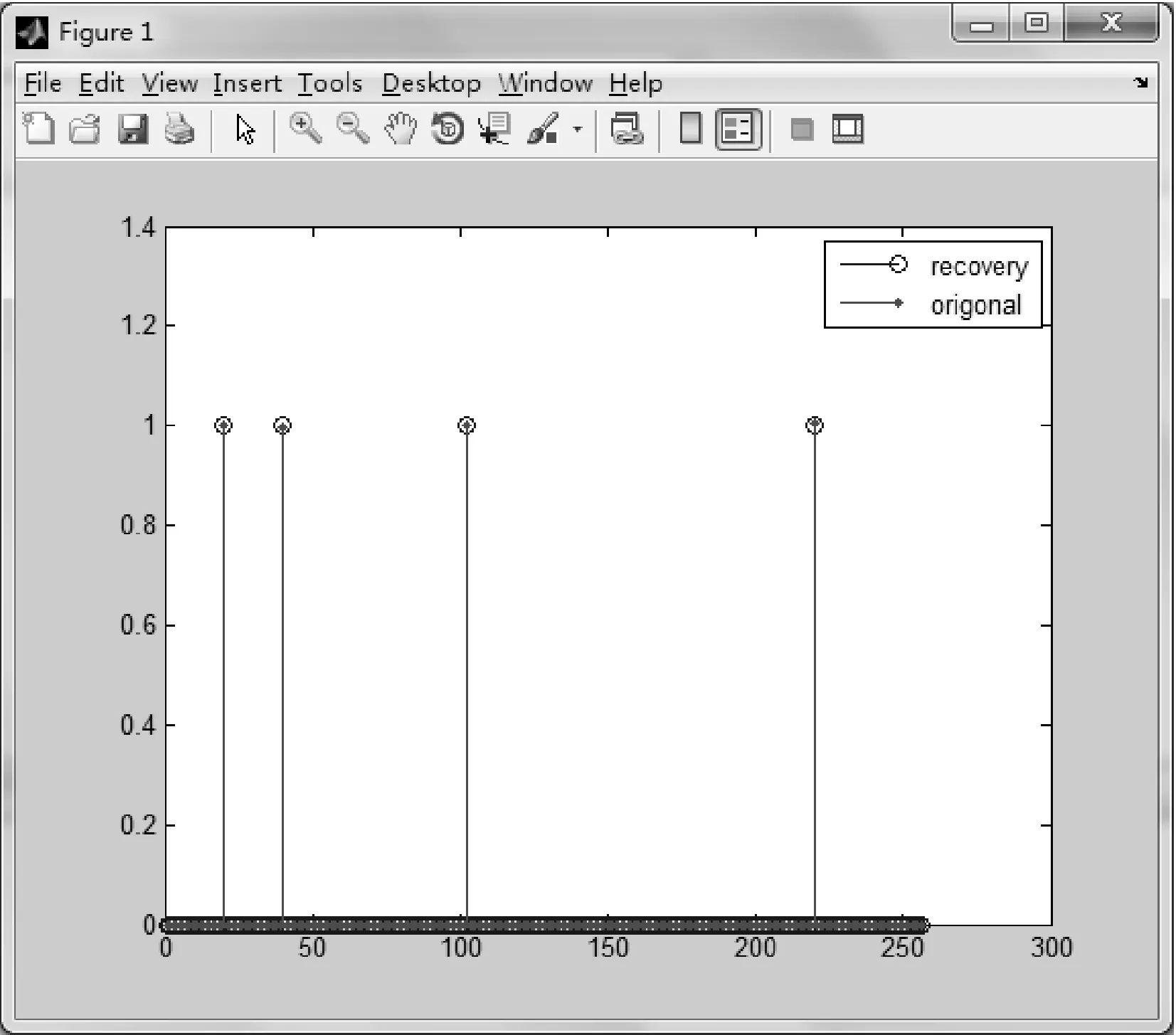
圖8　MP算法重構

可以看到m=40的時候,重構信號與原始信號有明顯偏差,這和重構算法的方法有關,這也證明了本文前面講過MP算法重構結果是次最優的不是最優的,而CoSaMP算法有著更高的精確度,后面將利用重構信號質量參數來評價重構質量。

3) 稀疏度K=10,測量次數m=70,信號長度n=1024。原始信號與重構信號對比如圖9所示。

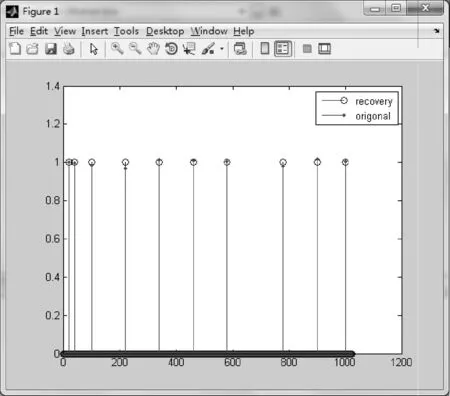
圖9　MP算法重構

4) 當信號長度增加到1024,測量次數為70或80,稀疏度為10的時候,在試驗過程中發現MP算法重構效果并不是很理想,而且不能保證很高的概率精確重構原始信號[10],出錯概率較大。所以需要增加測量次數。但是試驗結果由于受到算法本身限制,總會存在較明顯偏差,但經試驗發現當測量次數在300以上的時候是可以高概率重構出原始信號的,所以選擇測量次數m=500,試驗結果如圖10所示。

圖10　MP算法重構

通過MP算法和CoSaMP算法試驗結果對比,驗證了壓縮采樣匹配追蹤算法相對匹配追蹤算法有著更高的重構精確度,是一種在匹配追蹤算法基礎上改進了的重構算法。而匹配追蹤算法是較早出現的重構算法,有著本身的缺陷,在MP算法中,我們不能保證新的殘差與已選中的所有原子都正交,如果信號殘差在已選擇的原子進行垂直投影是非正交性的這會使得每次迭代的結果并不是最優從而需要多次迭代來進行收斂。

4.2重構質量參數評價

1) CoSaMP重構信號質量參數評價

論文前面對比了CoSaMP算法在不同稀疏度K和測量次數m的條件下其重構信號與原始信號的擬合程度,然而這只是表面上的對比,缺乏嚴謹的數據對比。因此本文在Matlab上模擬重構過程的時候添加了一段求解重構質量參數的程序,下面將從實驗所得到的參數數據來分析對比不同重構算法的重構效果。

(1)稀疏度K=4,信號長度n=256,測量次數m等于40和100的時候,所測得的質量參數值如表1所示。

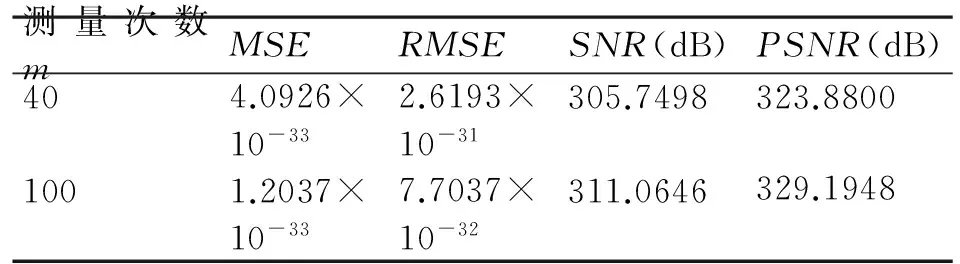
表1　CoSaMP重構信號質量參數

通過以上實驗數據對比,測量次數為100所得到的參數值中,均方誤差(MSE)和均方根誤差(RMSE)都要小于測量次數為40所得到的參數值,而信噪比(SNR)和峰值信噪比(PSNR)都大于測量次數為40所得到的參數值。論文前面講過,均方誤差(MSE)和均方根誤差(RMSE)都是越小越好而信噪比(SNR)和峰值信噪比(PSNR)是越大越好。說明在一定范圍內測量次數越大重構精密度越高,去噪效果更好,重構信號失真度越小。

(2)稀疏度K=10,信號長度n=1024,測量次數分別為70和80時測得的質量參數數據統計如表2所示。

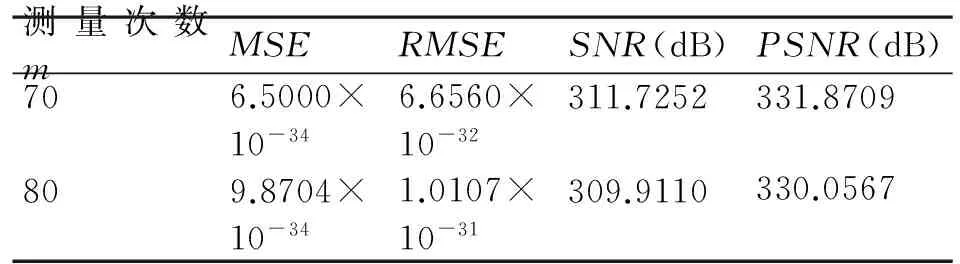
表2　CoSaMP重構信號質量參數

這組數據和前面稀疏度為4測得的數據較接近,其均方誤差和均方根誤差都非常小,信噪比和峰值信噪比比都比較大,說明兩種情況下重構信號質量都非常好。這也說明CoSaMP重構算法是一種精密度很高的重構算法。然而在這組數據中,測量次數m=80得到的均方誤差和均方根誤差都要大于m=70試驗得到的參數值,同時信噪比和峰值信噪比都要小于m=70得到的參數值,這與稀疏度為4測得的結果相反,說明并不是測量次數越高重構信號越好,只是在一定范圍內是隨著測量次數增加重構信號質量越好,超過一定范圍重構信號質量會隨著測量次數增加緩慢下降。

2) MP算法重構信號質量參數評價

下面將通過MP算法的重構質量參數值繼續分析稀疏度和測量次數對重構信號的影響,并對比CoSaMP算法重構信號的質量。

(1)稀疏度K=4,信號長度為256,測量次數分別為100和40所測得的質量參數數據統計如表3所示。

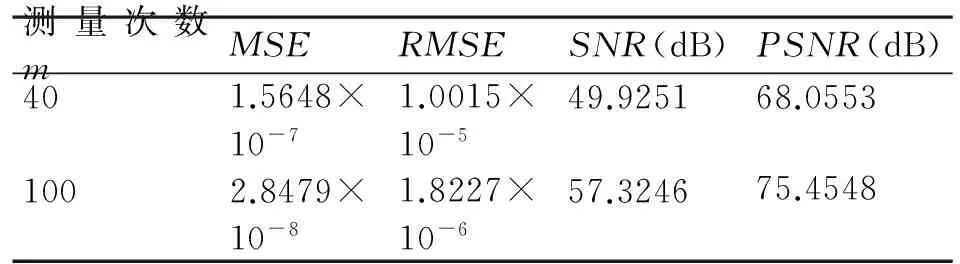
表3　MP重構信號質量參數

由表3中數據可以看出,測量次數為100所得到的參數值中,均方根和均方誤差明顯要小于測量次數為40所得到的參數值,而其信噪比和峰值信噪比都要大于測量次數為40所得到的參數值。這相應符合測量次數在一定范圍內,測量次數越大重構信號質量越高的結論。通過對比CoSaMP算法所測得的參數值,MP算法重構信號的均方和均方根誤差都要明顯大于CoSaMP重構算法,同時其信噪比、峰值信噪比只是CoSaMP算法重構信號的五分之一左右。說明在相同的稀疏度和測量次數條件下,中子脈沖信號使用CoSaMP重構得到重構信號的精密度和失真度都要好于MP重構算法。

(2)稀疏度K=10,信號長度n=1024,測量次數分別為70和500,試驗所測得的質量參數值如表4所示。

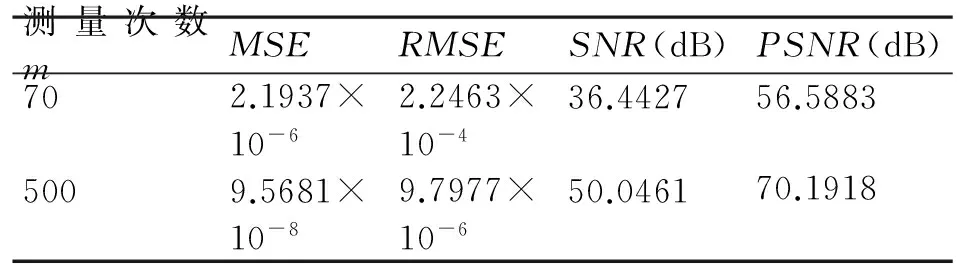
表4　MP重構信號質量參數

經過多次試驗發現稀疏度為10信號長度n=1024的時候,MP算法在測量次數小于200時,重構信號出錯率相當大,測量次數高于200后雖然重構概率比較高但重構信號明顯誤差較大,所以選取m=70時得到的未出錯信號和m=500時得到的重構信號質量參數值。此時得到的參數值同表3中數據值比較接近,但與CoSaMP算法得到的參數值同樣相差非常大。通過對比說明重構信號質量是和重構算法精密聯系的,測量次數只要達到一定值,在相同算法下重構信號比較接近但也有差別。重構信號質量[11]主要還是取決于算法本身方法問題。

5結語

本文主要研究了壓縮感知匹配追蹤類算法,作為最早實現的算法,很多改進了的算法都是基于貪婪匹配追蹤算法的算法思想上改進的。本文是在Matlab上實現MP和CoSaMP算法編程,并對中子脈沖信號實現重構過程。實驗結果表明CoSaMP壓縮采樣匹配追蹤算法是一個非常先進的重構算法,從實驗結果數據可以看出相比MP其重構效果非常好,重構精密度高,失真度小。

參 考 文 獻

[1] Emmanuel Candès. Compressive sampling[C]//Proceedings of International Congress of Mathematics, Madrid, Spain, 2006,3:1433-1452.

[2] Blumensath T, Davies M E. Gradient pursuits[J]. IEEE Transactions on Signal Processing,2008,56(6):2370-2382.

[3] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[4] Candes E. Compressive sampling[C]//Proceedings of In-ternational Congress of Mathematicians. Madrid, Spain: European Mathematical Society Publishing House,2006:1433-1452.

[5] 侯坤.基于壓縮感知的重構算法研究[D].重慶:重慶大學,2013:12-18.

HOU Kun. Research on reconstruction algorithms of compressed sensing[D]. Chongqing: Chongqing University,2013:12-18.

[6] 杜科.核信息系統的隨機核信號頻譜分析研究[D].重慶:重慶大學,2008:11-19.

DU Ke. Research on Nuclear random signal spectrum analysis of INIS[D]. Chongqing: Chongqing University,2008:11-19.

[7] 李樹濤,魏丹.壓縮傳感綜述[J].自動化學報,2009,35(11):1370-1379.

LI Shutao, WEI Dan. Compressed Sensing Survey[J]. Journal of Automation,2009,35(11):1370-1379.

[8] 石光明,劉丹華,高大化等.壓縮感知理論及其研究進展[J].電子學報,2009,37(5):1070-1081.

SHI Guangming, LIU Danhua, GAO Dahua, et al. Compression Theory and Research Progress perception[J]. Journal of Electronics,2009,37(5):1070-1081.

[9] Blumensath T, Davies M E. Stagewise weak gradient pursuits. Part I Fundamentals and numerical studies(Preprint, 2008)[EB/OL]. http://www.dsp.ece.rice.edu/cs.

[10] Blumensath T, Davies M E. Stagewise weak gradient pursuits. Part II Theoretical properties(Preprint, 2008)[EB/OL]. http://www.dsp.ece.rice.edu/cs.

[11] 任勇,米德伶,馮鵬.一種中子脈沖序列信號實時頻譜分析的研究[J].核電子學與探測技術,2009,29(4):876-881.

REN Yong, MI DeLing, FENG Peng. Study of a neutron pulse train signal in real-time spectrum analysis[J]. Nuclear Electronics & Detection Technology,2009,29(4):876-881.

收稿日期:2016年1月5日,修回日期:2016年2月13日

作者簡介:王銀,女,碩士研究生,研究方向:嵌入式、人工智能、物聯網技術。賀愛玉,男,工程師,研究方向:測控技術。

中圖分類號TP301.6

DOI:10.3969/j.issn.1672-9722.2016.07.006

Neutron Pulse Signal Reconstruction Algorithms

WANG Yin1HE Aiyu2

(1. School of Computer Science and Engineering, Anhui University of Science and Technology, Huainan232001)(2. College of Optoelectronic Engineering, Chongqing University, Chongqing404100)

AbstractIn this paper, with a neutron pulse data as the research object, combined with compressed sensing algorithm, neutron experimental data is simulated, matching pursuit algorithm and compressive sampling matching pursuit algorithm are used to reconstruct the neutron pulse signal on Matlab. By changing the measurement times and sparsity of signal, combined with parameters of SME, RMSE, SNR and PSNR etc, the reconstruction of compressed sensing framework neutron pulse signal is analyzed.

Key Wordscompressed sensing, matching pursuit, reconstruction algorithm, neutron pulse signal, quality parameters