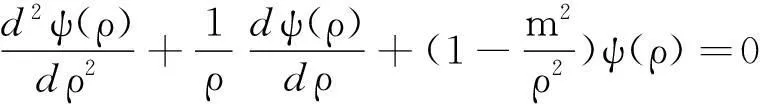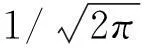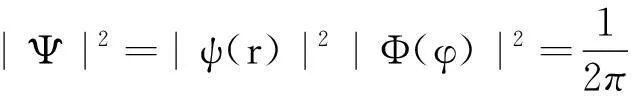有限高量子圍欄中電子的能級和波函數

江俊勤

(廣東第二師范學院 物理與信息工程系， 廣東 廣州 510303)

?

有限高量子圍欄中電子的能級和波函數

江俊勤

(廣東第二師范學院 物理與信息工程系， 廣東 廣州 510303)

摘要:用數值分析的方法對有限高量子圍欄內電子的能級和波函數進行全面的研究，糾正了現有文獻中的一些紕漏. 借助Mathematica強大的計算能力和杰出的數字繪圖功能，給出了能級圖和三維概率分布圖.

關鍵詞:有限高量子圍欄; 修正的貝塞爾函數；能級; 概率分布

1993年，克羅米(M. F. Crommie)等人使用掃描隧道顯微鏡(STM)將48個鐵原子吸附在銅表面上并排列成一個半徑為71.3 ?的圓環，鐵原子的平均間距為9.5 ?，這個原子圓圈能將銅表面上的電子圍住，所以這樣的原子圈被稱為“量子圍欄”或“原子圍欄”，該實驗通過STM觀測到了圍欄內電子概率的駐波圖.

這是人類第一次直接觀測到的電子駐波圖，對于物理學的理論和應用都具有極其重要的意義，因此已有多位作者通過求解定態Schr?dinger方程來解釋圍欄內電子的駐波現象，文獻[1]把問題簡化為無限高圍欄并計算了電子的能級和波函數, 但是無限高圍欄顯然與實際量子圍欄存在差距；文獻[2]和[3]考慮了有限高圍欄，但由于圍欄的外面是無限的自由平面，電子不被圍欄束縛、其能量不能具體確定；文獻[4]討論了高度有限而厚度無限的圍欄模型，這樣的量子圍欄能把能量低于圍欄高度的電子束縛在其內部，電子具有確定的能級和本征波函數，可惜的是文獻[4]沒有對電子的能級和狀態進行全面的研究，而且計算過程存在多處紕漏.

本文借助Mathematica強大的計算能力和杰出的數字繪圖功能，對高度有限而厚度無限的圍欄內的電子態進行全面深入的研究：糾正了文獻[4]的一些紕漏、 討論能級數目與圍欄尺寸的關系、繪制出能級圖和三維概率分布圖.

1 定態Schr?dinger及其貝塞爾函數解

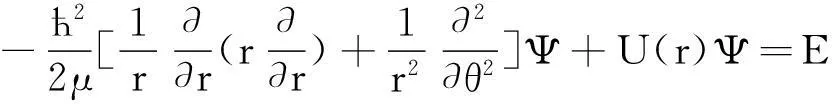
(1)

用分離變量法求解，令Ψ=ψ(r)Φ(φ)，代入(1)式，得

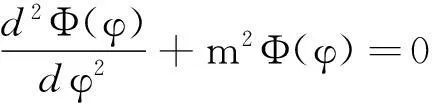
(2)

和

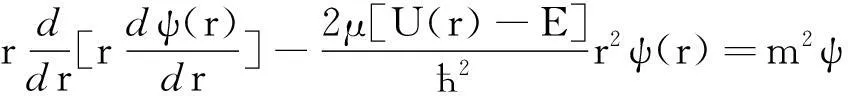
(3)

(2)式的解為

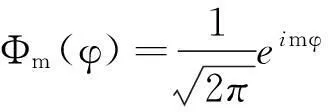
(4)

式中,m為角量子數(決定軌道角動量的大小)，由波函數單值性的要求Φm(φ+2π)=Φm(φ), 可得m=0,±1,±2,…； |m|的最大值由R和U0的大小決定，具體取多少，將在后面進一步討論.

圓內外的勢能不同，(3)式必須分兩個區域求解.

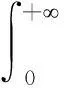
當0≤r

(5)

式(5)是標準的貝塞爾方程，有兩個獨立的解Jm(ρ)和Ym(ρ)，分別為第一類貝塞爾函數和第二類貝塞爾函數.

但是Ym(0)→-，不符合波函數有限性要求(ψ(0)=有限值)，所以符合波函數有限性要求的解為

ψ(ρ)=c1Jm(ρ)(0≤r

當r≥R時, 若令β2=k2(U0-E)，ρ=βr，則

(6)

式(6)也有兩個獨立的解Im(ρ)和Km(ρ)，分別稱為第一類修正的貝塞爾函數和第二類修正的貝塞爾函數.Im(+)→, 不符合波函數要求，所以符合波函數要求的解為ψ(ρ)=c2Km(ρ)(r≥R).

這是關于c1和c2的齊次線性方程組，有非零解的條件是系數行列式值等于0，

這是決定能量本征值的條件，求其數值解就可求得體系的能級. 第一個方程左邊接近于0，會影響計算精確度；第二個方程分母多處為零，會干擾正常計算；第三個方程最優越，令

(7)

則體系的能級為f(E)=0的根. 體系的徑向波函數可寫成

(8)

幾點說明：

(iii) 由于J-m(ρ)=(-1)mJm(ρ),K-m(ρ)=Km(ρ)，從式(7)和式(8)可知-m和m所對應的能級和徑向波函數是相同的，但是每一個能級有兩個角向波函數e±i|m|φ，所以能級是二度簡并的(m=0除外)；由于m的正負不影響能級和概率分布，所以在具體計算時可以只考慮m=0,1,2,….

2能級的數值結果

下面以Mathematica為工具，取圍欄的半徑為R=71.3 ?、圍欄的高度為U0=0.5 eV，對圍欄中電子的能級和波函數進行具體計算，并繪制概率分布圖.

圖1　當R=71.3 ?，U0=0.5 eV,m=0時f(E)的曲線圖

對應于m=0，f(E)的曲線如圖1所示. 在[0, 0.05]內E0初值太接近，可放大該區間再畫另一幅f(E)曲線圖(略)，從而確定E0的8個初值分別為0.004，0.022，0.052，0.09，0.16, 0.23, 0.32和0. 41(曲線在0.5處并未與橫軸相交).

圖2　當R=71.3 ?，U0=0.5 eV時f(E)的曲線實線:m=10；長劃線:m=21；短劃線:m=22

對于m=1,2,…的情況，用同樣的步驟逐一繪制f(E)的曲線圖，結果發現: 對于固定圍欄半徑R和高度U0，隨著m的增大f(E)=0的實根個數逐漸減少；對于R=71.3 ?和U0=0.5 eV，當m=10時只有四個實根(E=0不是本問題的解，不計算在內)，當m=18～21時都只有一個正實根(與橫軸正向只有一個交點)，從m=22開始沒有實根，圖2給出了m=10，21和22時f(E)的曲線. 所以對應于這樣的圍欄參數，角量子數的取值范圍為m=0,±1,±2,…,±21(對應的初值不在這里一一列出).

表1 給出了m=0,1,2,…,21所對應的能級個數(-m與m的能級數相同).

表1　有限高量子圍欄(R=71.3 ?和U0=0.5 eV)的角量子數及其能級個數N

所以當R=71.3 ?和U0=0.5eV時，能級個數為90；圍欄半徑R或者高度U0越大，m的取值范圍就越大. 如果把圍欄高度近似簡化為無限高，則m的取值范圍就是無窮(一切整數)，這就是文[1]的情形.

有了能級的大概值(找根的初值)，就可以尋找當R=71.3 ?和U0=0.5eV時m=0,1,2的能級了.對應于m=0的能級(以eV為單位，下同)分別為: 0.004 016 71, 0.021 154 6, 0.051 947 5, 0.096 326 5, 0.154 16, 0.225 217, 0.309 051和0.404 554；

圖3　前三個角量子數的能級總圖實線,長劃線，短劃線分別對應于m=0,1,2

對應于m=1的能級分別為: 0.010 196, 0.034 158 8, 0.071 757, 0.122 887, 0.187 376, 0.264 909, 0.354 822和0.454 964；

對應于m=2的能級分別為:0.018 3131, 0.049 154 6, 0.093 557 3, 0.151 414, 0.222 503, 0.306 39和0.402 018.把m=0,1,2三種不同角動量的能級畫在一起，得如圖3所示的能級總圖.

對于m=0,1,2三種不同角量子數，能級是很有規律的：從低到高分別是m=0,1,2的三個最低能級(m=0的第一個能級為基態能)，接著是m=0,1,2的三個次低能級(m=0的次低能級略高于m=2的最低能級)，…，最后是m=0的第八個能級及m=1的第八個能級．

如果把m=3,4,…,21的能級也一起排列，情況就復雜了，具體情況有待進一步計算.

3波函數與概率分布的數值結果

把已經得到的能級逐個代入式(8)即可確定每個能級所對應的波函數，借助Mathematica可以自動快速得到波函數，并繪制電子的概率分布圖(立體圖)，對于m=0，R=71.3 ?和U0=0.5eV，如圖4～圖11所示. 對于m=1，只給出第四個能級所對應的電子概率分布圖，如圖12所示；對于m=2，只給出第三個能級所對應的電子概率分布圖，如圖13所示.

以上結果表明：角動量為零 (m=0) 的量子態在圍欄中心(r=0)是概率主峰，角動量不為零 (m≠0) 的量子態在圍欄中心(r=0)是概率低谷(波函數的節點). 此外，不論角量子數m是多少，概率分布圖的波峰個數都與能級E(m,n)的序號n相一致.

最后，研究束縛態的最高能級(m=21, 即能量最接近0.5eV)的量子狀態，數值結果如圖14所示. 電子概率分布主要集中在圍欄邊緣.

圖14m=21的能級(唯一且最高的能級)所對應的概率密度

參考文獻：

[1] 周佩瑤，王萊，陳宜生. 原子圍欄中金屬表面電子的態函數及能級[J]．工科物理，2000，10(4)：9-11.

[2] 戴淇, 蔣平. 量子圍欄的電子結構(英文)[J].復旦學報(自然科學版), 2000, 39(2):132-134.

[3] 塔立, 單崳瓊, 周向仁, 等. 量子圍欄中的表面電子局域態密度及其模擬[J]．云南大學學報(自然科學版)，2009，31(S2)：411-416.

[4] 董建．Mathematica與大學物理計算 [M]．2版. 北京：清華大學出版社，2013：289-296.

收稿日期：2016-01-21

基金項目：廣東省高等學校專業綜合改革試點項目(2014)

作者簡介：江俊勤，男，廣東揭陽人，廣東第二師范學院物理與信息工程系教授.

中圖分類號：O562.1

文獻標識碼：A

文章編號：2095-3798(2016)03-0057-06

Energy Level and Wave Function of Electron inside Finite High Quantum Corral

JIANG Jun-qin

(Department of Physics and Information Engineering, Guangdong University of Education,Guangzhou，Guangdong, 510303, P.R.China)

Abstract:The energy levels and wave functions of the electron in the finite high quantum corral are numerically studied. Some errors in the existing literature are corrected. The energy level diagrams and the three dimensional probability distribution diagrams are given by using MATHEMATICA.

Key words:finite high quantum corral; modified Bessel function; energy level; probability distribution