基于多重非線性管-土耦合模型的管道應變設計方法

劉銘剛，楊秀娟，閆相禎，韓思旻，樊蘇楠

（1.中國石油大學（華東）儲運與建筑工程學院，山東 青島266580；2.中國石油大學（華東）油氣CAE技術研究中心，山東 青島266580）

基于多重非線性管-土耦合模型的管道應變設計方法

劉銘剛1，2，楊秀娟1，2，閆相禎1，2，韓思旻1，2，樊蘇楠1，2

（1.中國石油大學（華東）儲運與建筑工程學院，山東 青島266580；2.中國石油大學（華東）油氣CAE技術研究中心，山東 青島266580）

基于應變的管道設計方法是利用位移控制思想實現管道的極限狀態設計，是管道設計的發展方向。考慮材料非線性和載荷非線性建立管-土耦合模型進行基于應變的管道設計，以設計應變作為可靠度評價指標，建立埋地管道可靠度評價分析模型，通過對不同斷層參數和管道參數的分析，得出定量的管道可靠度結果。結果表明：管道的軸向最大拉伸應變和軸向最大壓縮應變隨斷層錯距與土壤內摩擦角增大而增加；壁厚、徑厚比、埋深對跨斷層埋地管道極限應變狀態影響很大，參數敏感性最大的是徑厚比；敏感性分析的結果可以作為埋地管道完整性評價模型的狀態變量。研究結果可為跨斷層埋地管道完整性評價及管道安全測試方法提供思路參考。

工程力學；管土耦合模型；管道應變設計；完整性；埋地管道

0　引　言

隨著天然氣管道運輸行業的飛速發展，尤其是長距離、埋地和跨斷層長距離輸氣管道日趨增多，這就對管道設計準則或標準提出了更高的要求，使之在經濟有效、節約成本的前提下保證管道安全運作。

管道完整性需從安全性、可靠性進行綜合評價。加拿大管道設計規范CSA Z662——2003最早提出基于應變控制的管道設計規范的系統方法［1］；國內的劉愛文［2］提出了應用數值方法研究埋地管道力學行為的三向土彈簧模型，為有限元方法應用于管道設計提供了思路指引；劉冰等［3］在位移控制載荷下的管道設計方面進行了研究，得到了位移載荷作用下的管道應變規律；有學者等對跨斷層埋地管道應用基于應變控制的選材規范進行了研究，指出由于設計作業區為管道材料的彈塑性段，傳統的基于應力的強度校核方法已經不適用的觀點［4-7］；王海霞等［8-10］提出管道完整性評價方法應將管道強度和失效統計數據作為評價內容。因此，從目前國內外領先的基于應變的管道設計方法出發，考慮此類管道設計中管材參數和載荷的隨機性和復雜性，提出結合有限元軟件Ansys的基于應變設計的管道完整評價方法，旨在通過成熟的結構可靠性理論，借助先進的數值模擬技術，同時考慮材料和載荷雙非線性，建立滿足精度的埋地管道“管-土”載荷-應變可靠性模型，對位移控制載荷作用下的埋地管道安全性和可靠性進行評價，為深入開展埋地管道完整性評價技術研究提供思路。

1　基于應變的管道設計

1.1基于應變的管道設計方法

基于應變的管道設計方法是利用位移控制思想實現管道的極限狀態設計，是管道設計的發展方向。國內現行的各類管道設計標準大多數都是遵循傳統的基于許用應力的設計準則。而在考慮地震、斷層、海底管道敷設等位移控制載荷進行管道設計時，為合理利用管材，保證工作應變超屈服應變時管道的安全運營，應采用基于應變的管道安全校核和設計方法［3］，埋地管道容許應變的計算參照文獻［4-7］中的方法。設計流程圖如圖1所示。

1.2跨斷層埋地管道管-土作用力學模型

考慮管土參數和載荷，采用等效土彈簧法模擬管-土之間相互作用［2］。斷層作用下管道載荷主要有：土對管道的作用載荷、管道內氣體的壓力載荷及遠端管道對分析段管道的約束載荷，力學模型如圖2所示。

選取含斷層載荷作用區域的管段建立有限元分析模型，管道物理模型采用SHELL181單元進行模擬，土體與管道之間的相互作用采用理想彈塑性土彈簧單元COMBIN39模擬，彈簧單元一端設置為管軸方向、水平橫向和垂直方向的土彈簧，并固定約束，另一端與管道模型單元連接。管道延伸段截面施加等效彈簧表模擬無限遠處管道對該段管道的作用力，有限元計算模型如圖3所示。模型采用SWEEP方式進行網格劃分。

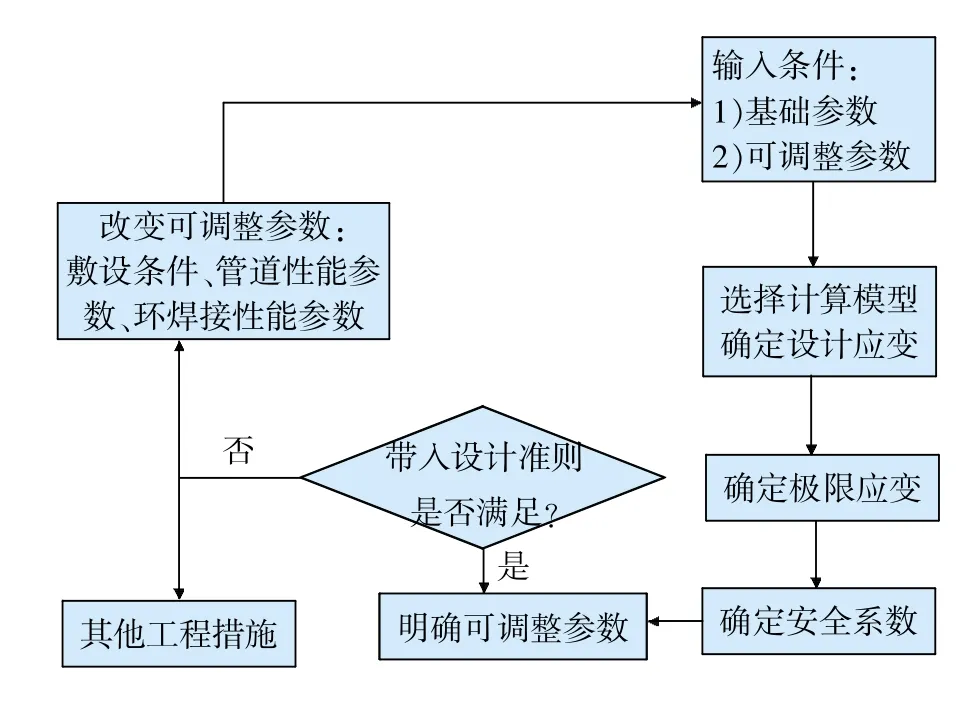
圖1　基于應變設計流程圖

圖2　埋地管道管-土作用力學模型示意圖

圖3　埋地管道管-土作用三維有限元模型

圖4為管道穿越斷層區相對位置示意圖，斷層傾角為φ，管道與斷層相交交角為β，斷層水平位移為δ1，垂直位移為δ2，管道受斷層引起的位移載荷作用，載荷分量有：垂向分量δ2sinφ、軸向分量δ2cosφsinβ+ δ1cosβ、水平向分量δ2cosφcosβ-δ1sinβ。

其中，δ2對正斷層取正值，對逆斷層取負值；δ1對右旋走滑斷層取正值，對左旋走滑斷層取負值。

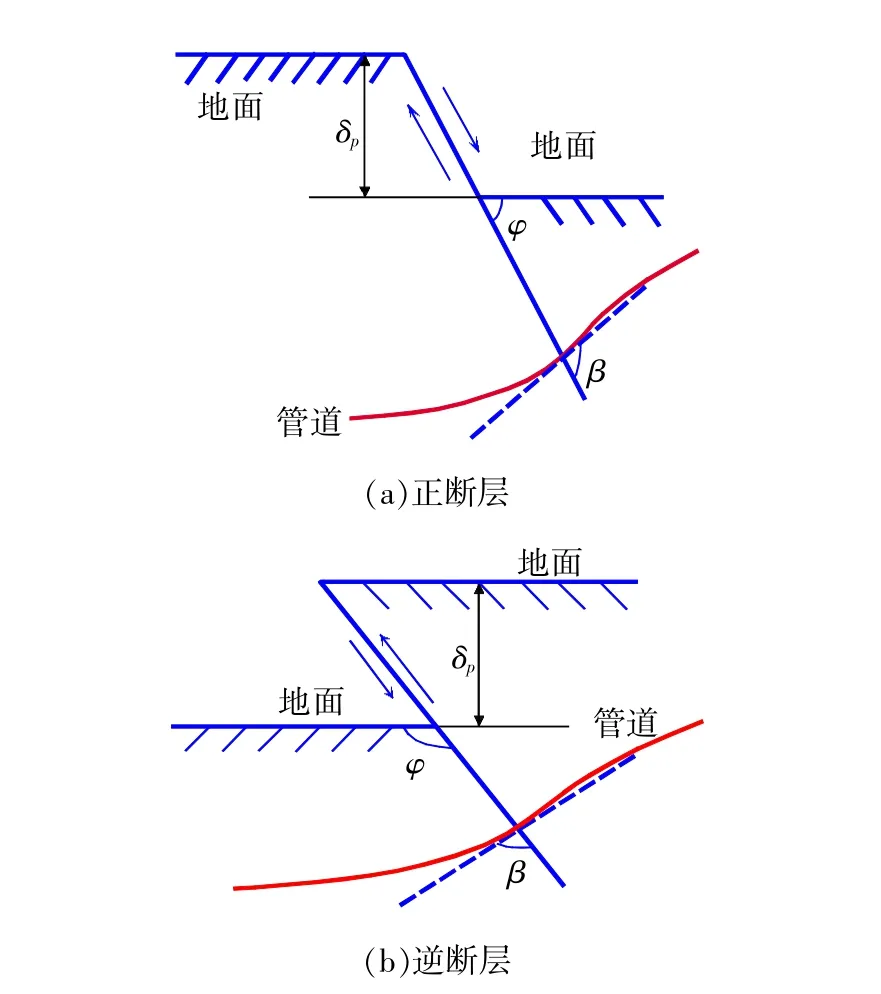
圖4　管道與斷層相交示意圖

2　基于應變設計的管道完整性評價方法

2.1輸氣管道事故原因及完整性

輸氣管道完整性即管道抵抗結構性破壞的能力。據歐美俄中多家輸氣公司數據顯示，油氣運輸管道事故中埋地管道完整性主要受外力損傷、腐蝕、材料缺陷、操作失誤等因素影響，在長距離埋地管道設計中，地震等自然災害引起的斷裂帶位移造成的管道完整性破壞是不可忽略的評價內容［9］，根據美國天然氣協會AGA的統計數據制出現役管道在多年運行過程中每年事故發生的原因統計圖，如圖5所示。

圖5　國外輸氣管道事故原因統計圖（單位：%）

從圖中可以看出，無論是普通管道還是埋地輸氣管道，導致輸氣管道事故發生最多的原因為外載作用，說明地震、土層位移等外載作用是造成管道完整性破壞的重要因素［10］。本文以跨斷層埋地管道所受位移載荷進行分析，從安全性和可靠性兩方面進行管道完整性評價。

2.2基于應變的管道安全性評價

與傳統基于設計應力的設計準則不同，基于應變設計的方法以設計應變作為管道安全的衡量指標，通過選取適當的安全系數進行安全校核，數學表達式如下式所示：

式中：εd——設計應變；

εcr——極限應變，包括極限拉伸應變、極限壓縮應變；

F——安全系數，F≥1，根據加拿大規范CSA Z662［1］附錄C選取。

基于應變設計方法是受位移控制載荷作用下，為保證管道在塑性變形下（應變≥0.5%）能夠滿足特定目標而進行的設計。當管道設計應變大于管道的容許應變能力時，管道校核不通過；當管道設計應變小于管道容許的應變能力時，管道才是安全的。

2.3基于應變設計的管道可靠性評價

根據圖3的埋地管道三維有限元模型，可以方便地求得確定載荷工況下的管道應變和極值。以軸向應變S為校核基準的跨斷層埋地管道可靠性極限狀態方程為

式中：W——管道可靠性的狀態值（正為滿足校核要求，負為不滿足校核要求，零值說明管道不發生失效的極限狀態）；

S0——管道材料的容許應變絕對值，%；

S——確定工況下管道的最大軸向應變絕對值，%。

由于管廠同一批管材容許應變分布規律和分布參數是可確定的，跨斷層埋地管道可靠度可由下式［11-14］求得：

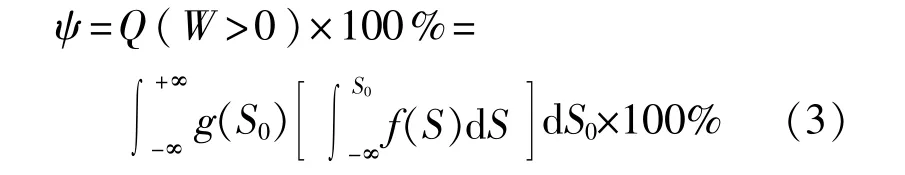
式中：ψ——管道的可靠度，%；

Q（·）——事件概率；

f（·）、g（·）——分別為管道容許應變和計算

應變的概率密度函數。

隨機樣本采用基于Monte-Carlo方法的Latin Hypercube抽樣法［15］。以有內壓工況為例，圖6和圖7分別為對最大軸向壓應變的抽樣過程和均值收斂曲線，模擬次數為1000次。

圖6　最大壓應變抽樣過程

圖7　最大壓應變均值收斂曲線

從圖中可以看出，當模擬次數超過500次后，均值收斂性已非常好，其模擬均值和精確值誤差≤0.002（如圖7），完全可以滿足本文的計算要求，因此本文模擬次數設定為1000次，置信度95%。抽樣完成后通過靈敏度分析確定影響管道可靠性的因素排行，作為管道完整性的隨機因素評價指標。

圖8　無內壓和有內壓跨斷層埋地管道有限元結果應變云圖

表1　土彈簧參數設置值

表2　埋地管道穿越開墾河斷裂帶載荷參數表

3　工程實例

3.1基于應變的跨斷層埋地管道校核及規律研究

某長距離跨斷層埋地管道工程選用1 219mm× 26.4mm HS鋼管，回填土為沙土，根據美國ASCE——2003埋地管道設計規范［16］進行土彈簧參數設置，如表1所示，模型單元總數為180000。

管道埋深1.8m，設計內壓為12MPa。考慮管道穿越典型斷裂帶（以開墾河斷裂帶為例）工況，具體參數見表2和表3。

軸向應變計算結果如圖8和表3所示。從圖表中可以看出，無內壓時，開墾河斷裂帶穿越管道設計應變均小于容許應變，校核通過；有內壓時，設計壓縮應變為1.01%，大于容許應變0.90%，校核不通過，即管道安全完整性被破壞。通過安全性評價可以得到跨斷層埋地管道在確定工況下完整性表現。

埋深選取為2.1m，斷層傾角為60°，斷層與管道交角為90°，研究水平錯距為1m，垂向錯距為0.5，1.0，1.5，2.0，2.5，3.0，3.5，4.0m時管道不同點處軸向應變變化規律，管道軸向最大應變與錯距的關系曲線如圖9所示。可以看出，埋地管道的軸向最大拉伸應變和軸向最大壓縮應變小于容許應變時，軸向最大拉伸應變和軸向最大壓縮應變隨著錯距的增加而增加。

表3　埋地管道穿越開墾河斷裂帶計算結果表

圖9　軸向最大拉伸應變隨錯距變化曲線

土壤的內摩擦角分別取20°，30°，35°，40°，45°，其他采用基本數據。經分析運算，在管道與斷層交角90°的正斷層情況下，管道軸向最大拉伸拉應變和最大壓縮應變的分布如圖10所示。可以看出，在相同斷層錯距的作用下，隨著內摩擦角的增大，埋地管道的軸向最大拉伸應變和軸向最大壓縮應變逐漸增加。

3.2跨斷層管道可靠性分析結果

影響管道完整性還包括跨斷層埋地管道設計中的隨機因素。影響管道失效可靠度的輸入參數及概率分布如表4所示。

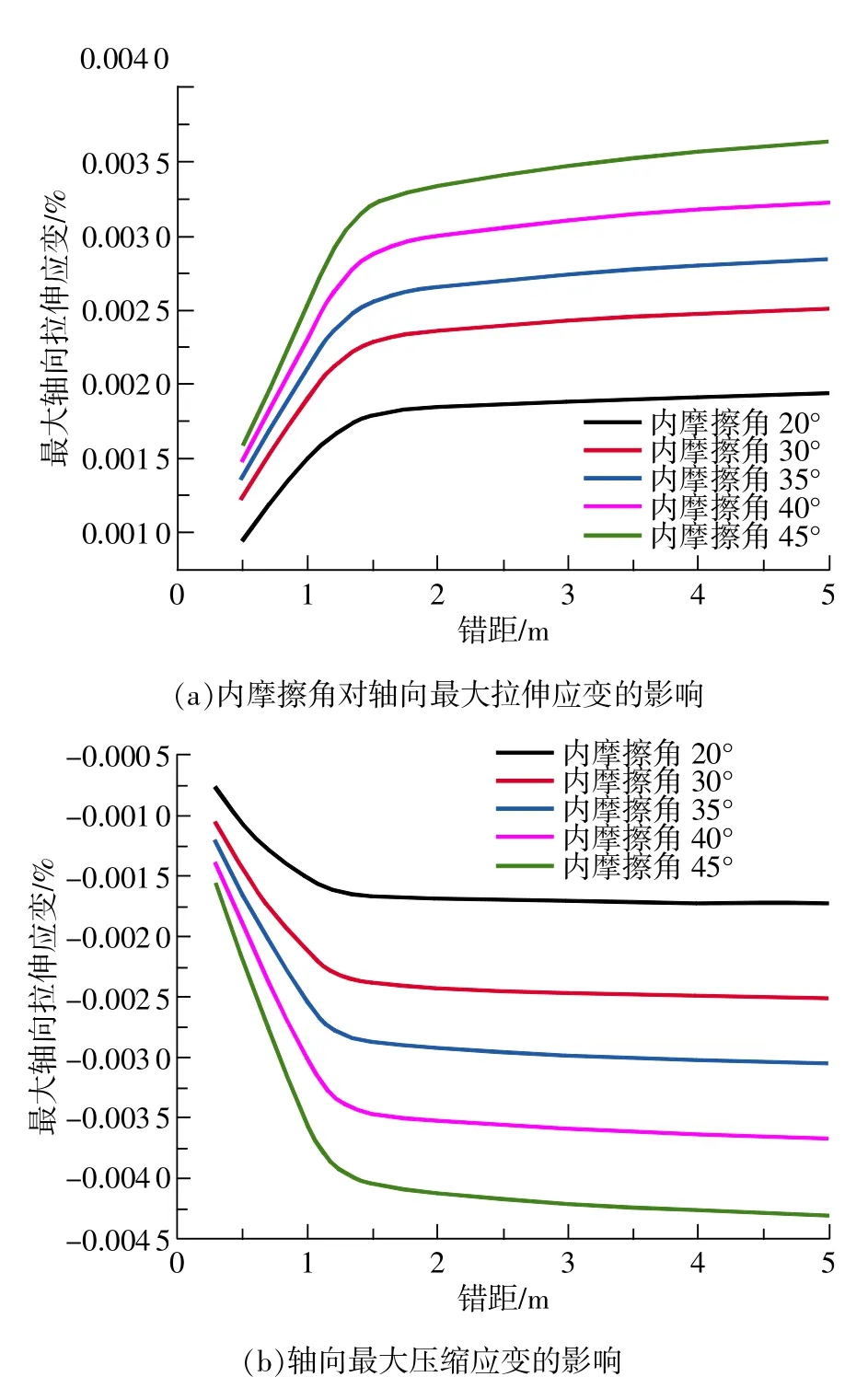
圖10　內摩擦角對軸向最大拉伸應變和軸向最大壓縮應變的影響

表4　輸入參數及概率分布類型

圖11為埋地管道可靠性狀態值W的概率密度柱狀圖。可以看出管道的可靠性函數基本服從正態分布，其可靠度為91.53%。

表5　各因素對套管可靠性的影響情況

圖11　管道可靠性狀態概率密度曲線

表5為跨斷層埋地管道設計中的隨機因素，如位移載荷、內壓、埋深、土壤內摩擦角，以及管材的密度、幾何尺寸和本構關系等，對管道可靠性的影響程度（以置信度95%計算）。表中數值絕對值表示相應因素對埋地管道可靠性影響程度的大小，數值正負表示該因素對套管可靠性的益弊情況。從表中可以看出，管道徑厚比對其可靠性影響程度最大，合理的徑厚比對管道抵抗位移載荷有明顯幫助；當斷層參數基本確定的情況下，壁厚、埋深對跨斷層埋地管道極限應變狀態影響很大。

4　結束語

跨斷層埋地管道完整性評價主要包括管道安全性和可靠性兩部分。考慮此類管道設計中管材參數和載荷的隨機性和復雜性，建立滿足精度的埋地管道“管-土”作用載荷-應變可靠性模型進行管道可靠度分析，對位移控制載荷作用下的埋地管道安全性和可靠性進行評價，得到以下結論：

1）管道的軸向最大拉伸應變和軸向最大壓縮應變隨斷層錯距與土壤內摩擦角增大而增加。

2）壁厚、徑厚比、埋深對跨斷層埋地管道極限應變狀態影響很大，參數敏感性最大的是徑厚比。

3）敏感性分析的結果可以作為埋地管道完整性評價模型的量化參數。

［1］Oil and gaspipeline systems：CSA Z662-2003［S］.Canadian Standards Association，2003.

［2］劉愛文.基于殼模型的埋地管線抗震分析［D］.北京：中國地震局地球物理研究所，2002.

［3］劉冰，劉學杰，張宏.以應變為基礎的管道設計準則及其控制因素［J］.西南石油大學學報（自然科學版），2008，30 （3）：143-147.

［4］劉冰，劉學杰，張宏，等.基于應變的管道設計準+則［J］.天然氣工業，2008，28（2）：129-131.

［5］劉學杰，孫紹平.地下管道穿越斷層的應變設計方法［J］.特種結構，2005，22（2）：81-85.

［6］余志峰，史航，佟雷，等.基于應變設計方法在西氣東輸二線的應用［J］.油氣儲運，2010，29（2）：143-147.

［7］韓冰，王芝銀，吳張中，等.基于應變理論在采空區管道失效分析中的應用 ［J］.中國石油大學學報 （自然科學版），2012，36（4）：134-138.

［8］王海霞，范瑋.在役輸氣管線的完整性評價方法［J］.管道技術與設備，2008（3）：4-5.

［9］付小方.天然氣輸送管道風險評價與完整性評定［D］.廣州：華南理工大學，2011.

［10］錢成文，劉廣文，高穎濤，等.管道的完整性評價技術［J］.油氣儲運，2000（7）：11-15.

［11］孫建宇.輸氣管道完整性管理簡介［J］.石油庫與加油站，2009，18（3）：14-17.

［12］張駿華.結構可靠性設計與分析［M］.北京：宇航出版社，1989.

［13］盛驟，謝式千，潘承毅.概率論與數理統計［M］.北京：高等教育出版社，1989.

［14］劉惟信.機械可靠性設計［M］.北京：清華大學出版社，1996.

［15］Ansys Incorporated.Ansys Release Document［Z］.Ansys Help.

［16］The American Society of Civil Engineers.Guidelines for the design of buried steel Pipe［M］.American Lifelines Alliance，2001：57.

（編輯：劉楊）

Strain design analysis method of buried pipeline based on multiple nonlinear pipe-soil coupling model

LIU Minggang1，2，YANG Xiujuan1，2，YAN Xiangzhen1，2，HAN Simin1，2，FAN Su'nan1，2
（1.College of Pipeline and Civil Engineering，China University of Petroleum，Qingdao 266580，China；2.Oil and Gas CAE Technology Research Center，China University of Petroleum，Qingdao 266580，China）

Strain analysis method for pipeline is a limit state design way base on displacement control theory which can be the new direction of pipeline design.Taking designed strain as reliability evaluation index and considering the material nonlinearity and load nonlinearity and different parameters of the fault and pipe，pipe-soil coupling model based on strained pipeline design is established and quantitative reliability result of pipeline is proposed.The result shows：The maximum axial tensile strain and compressive strain rises as the staggered distance and internal friction angle of soil grows；Wall thickness，radius to thickness ratio and buried depth of the pipe have great influence on the strain of buried pipeline at crossing-fault and the radius to thickness ratio has the greatest parameter sensitivity；The results of sensitivity analysis can be used as the state variables of the integrity assessment of pipeline.The studying conclusions can provide ideas and reference for the integrity assessment of crossing-fault buried pipeline.

engineering mechanics；pipe-soil coupling model；pipeline strain design；integrity；buried pipe

A

1674-5124（2016）07-0009-06

10.11857/j.issn.1674-5124.2016.07.002

2015-11-22；

2016-01-07

國家自然科學基金項目（51274231，51374228）；國家自然科學基金-石化聯合基金項目（U1262208）；CNPC重點實驗室課題（2014A-4214）；中央高校基本科研業務費專項資金（15CX06067A）

劉銘剛（1990-），男，博士研究生，研究方向為油氣工程力學、機械強度及可靠性。