變分貝葉斯獨立分量分析在諧波狀態估計中的應用

韓　斐，楊洪耕，王佳興，王　澤（四川大學電氣信息學院，成都　610065）

變分貝葉斯獨立分量分析在諧波狀態估計中的應用

韓斐，楊洪耕，王佳興，王澤
（四川大學電氣信息學院，成都610065）

針對實際電網中諧波阻抗難以準確獲取，且量測噪聲不可避免的問題，提出利用變分貝葉斯獨立分量分析VBICA（variational Bayesian independent component analysis）進行配網諧波狀態估計。該方法將諧波阻抗和量測噪聲作為未知參數，利用變分貝葉斯理論計算獨立分量分析模型中未知參數和潛在諧波電流的后驗概率分布，通過迭代學習提取不受噪聲干擾的諧波電流最優值。再結合負荷等效導納遠小于系統等效導納的特點，推導出幅值比例系數，計算諧波電流幅值。利用IEEE 33節點配網系統對該方法進行驗證，并將該方法與傳統獨立分量分析法進行對比，結果表明該方法具有更高的估計精度和更強的抗干擾能力。

諧波狀態估計；變分貝葉斯；獨立分量分析；未知諧波阻抗；噪聲干擾

DOI：10.3969/j.issn.1003-8930.2016.04.012

分布式發電的快速發展和非線性負載的大量增加，加重了配電網的諧波污染［1-2］。為有效治理諧波并節約成本，預先了解該地區電網的諧波分布和狀態具有重要意義［3］。

諧波狀態估計可根據有限節點的諧波量測估計全網諧波分布和狀態，其最終目的是估計電網中諧波源位置和諧波電流幅值［4-7］。文獻［3］首次提出諧波狀態估計技術進行諧波源識別，并指出諧波源識別的判據。文獻［5］利用電網中諧波源數量較少的特點，將節點分為可疑諧波源節點和非諧波源節點，利用有限量測量估計諧波狀態。文獻［6］利用加權最小二乘法求解量測方程，得到諧波狀態最優解。文獻［7］基于諧波源分布的空間稀疏性，利用稀疏表示法進行諧波狀態估計。

諧波狀態估計技術需要精確的諧波阻抗和網絡拓撲，但由于電網運行受隨機因素影響，以及元件參數的分散性［8］，精確的諧波阻抗和網絡拓撲難以獲取［9］，網絡參數的缺失會嚴重影響估計精度。諧波阻抗和網絡拓撲未知情況下，諧波狀態估計可作為盲源分離問題，通過獨立分量分析ICA（in?dependent component analysis）求解［10］。

ICA在電力系統已得到廣泛應用［9-16］。在諧波分析方向，文獻［9-11］忽略噪聲干擾，采用復值ICA估計諧波電流，得到諧波電流實部和虛部變化曲線，但沒有進一步估計諧波電流幅值。文獻［12-13］利用ICA從電壓量測信號中分離出諧波信號，實現了諧波源辨識。文獻［14］采用含噪ICA進行諧波源定位，從量測數據協方差矩陣中減去噪聲協方差矩陣，以消除噪聲影響，但噪聲大小通常是未知的，且沒有確定諧波電流的幅值。

鑒于此，本文采用變分貝葉斯獨立分量分析VBICA（variational Bayesian independent component analysis）估計諧波電流。將ICA模型中的噪聲、阻抗參數等作為未知變量，將諧波電流作為隱藏變量，利用變分貝葉斯VB（variational Bayesian）對未知量的學習能力，得到不受噪聲干擾的諧波電流最優解。并根據線性負荷導納遠小于系統側導納的特點，忽略線性負荷導納，推導出諧波電流幅值比例系數，確定電流幅值。采用IEEE 33節點配電網絡對該算法進行驗證，結果表明該方法能夠在含噪情況下準確估計諧波電流幅值，驗證了該方法的有效性。

1　VBICA原理

存在噪聲干擾的ICA數學模型為

式中：Xt為M維觀測信號；A為M×N維混合矩陣；St為N維源信號；ε為M維零均值高斯噪聲信號，t= 1，2，…，T為樣本點數。

將該ICA模型運用于VB框架中，給出觀測信號和未知參數的先驗概率分布。觀測信號X（t）的條件概率分布為

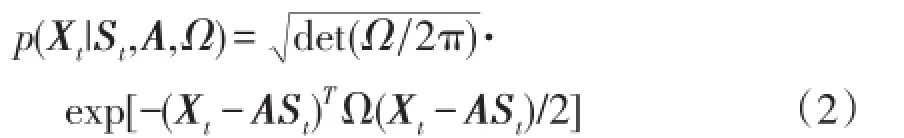
式中：Ω為高斯噪聲協方差；det表示求矩陣行列式；exp表示以自然常數e為底的指數函數。觀測矩陣X的條件概率分布為

源信號S后驗概率分布計算式為

式中：W為某一具體模型，須選擇符合源信號特性且易于計算的模型；p（S|X，W）為源信號S的后驗概率；p（X|S，W）為觀測信號X的后驗概率；p（S|W）為信號源模型［17］；p（X|W）為規范因子，通常為模型W的邊際概率。

由中心極限定理，ICA模型中的非高斯源信號混合后接近高斯分布，因此選用高斯混合MOG（mix?ture of Gaussians）模型表示源信號的概率分布，即

式中：ν為M維源信號S的參數，ν=［σ，e，α］；σ為混合比例系數；e和α分別為源信號矩陣中每個元素的期望值和精度；i為源信號編號；t為第i個源信號的第t個成分。

參數ν的先驗概率分布為

式中：p（ν）定義為Dirichlets分布的乘積；p（σ）定義為混合比例系數的先驗分布概率；p（e）和p（α）分別定義為高斯分布和Gammas分布的乘積。

ICA模型中混合矩陣A的先驗分布定義為高斯分布的乘積，噪聲協方差矩陣的先驗分布定義為Gammas分布的乘積。

給定各參數和觀測值的先驗分布，采用變分近似逼近算法進行VBICA模型的學習。ICA模型中未知參數和潛在變量的后驗概率分布計算式為

式中：θ=｛A，S，Ω，ν｝包括未知參數和潛在變量；p（θ |X，W）表示未知參數和潛在變量的后驗概率分布；p（X|θ，W）表示觀測信號的后驗概率；p（θ|W）表示未知參數和潛在變量的概率。

以損失函數最小化，即負自由能最大化為目標函數：

式中：p′（W）表示模型W的先驗概率的一階導數；H（′（W）表示p′（W）的熵；p（X，θ|W）表示X和θ的聯合分布概率。

忽略θ各成分間的弱相關性，p′（θ|ν）的計算式為

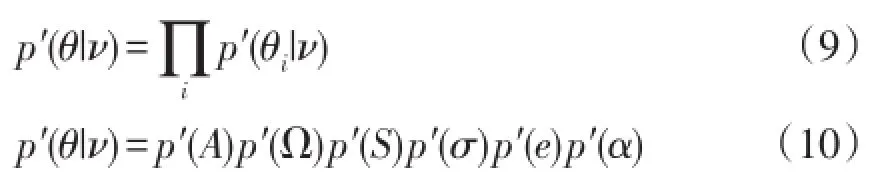
式中，p′（?）表示括號內變量概率的一階導數。

分別求p′（θ|ν）對各參數的偏導數，可得到未知參數的估計值。

由ICA模型中

式中，p（?）表示括號內變量的先驗概率。

將式（10）、（11）代入式（8），可得到源信號的近似后驗概率分布為

類似可推導其他未知變量的后驗分布，并迭代求解直至收斂。

2　VBICA在諧波狀態估計中的應用

2.1ICA與諧波狀態估計

含諧波源網絡的某次諧波節點電壓方程為

式中：h為諧波次數；Vh為節點諧波電壓；Zh為節點阻抗矩陣；Ih為注入諧波電流。為簡化起見，以下省略變量的下標h。

ICA要求源信號為統計獨立的非高斯分布，利用平滑濾波器提取的諧波電流快波動分量之間具有較低的相關性，且為超高斯分布［10］，滿足ICA的要求。平滑濾波器不改變變量間的關系，即

式中：上標f代表快波動分量；上標s代表慢波動分量。

由于電壓電流相量及諧波阻抗均為復值，本文將復值ICA與VB結合來估計諧波電流。復值ICA的目標函數［18］為

式中：w為復數分離向量；上標H表示共軛轉置；x為量測量；E為數學期望；G（y）=asinh y，表示獨立分量的近似負熵；y為待提取的獨立分量，y=wHx。

以量測節點的諧波電壓Vm為量測量，以諧波源電流I為狀態量，利用平滑濾波器提取量測量的快波動分量，建立量測方程為

利用VBICA僅能得到次序和幅值不確定的諧波電流。為準確估計諧波電流，須消除這種不確定性。

2.2消除不確定

確定諧波電流次序：將各支路的導納值設為1，建立象征導納矩陣［13］Ysym，求逆得到阻抗矩陣Zsym，將Zsym和混合矩陣A的各列分別進行歸一化得到矩陣Znorm和Anorm，并按下式計算兩個矩陣中匹配度最高的列，得到確定次序的諧波電流Iseq和混合矩陣Aseq。

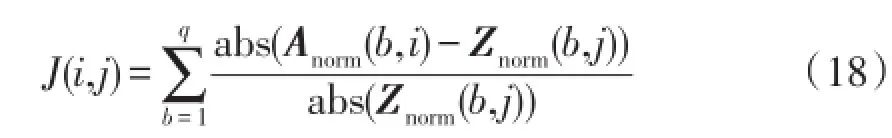
式中，abs表示絕對值運算。

確定諧波電流幅值：設節點1為配電網的根節點，在根節點處配置量測裝置，由此可得到根節點處系統短路電抗xk為

式中：h為諧波次數；V1m根節點電壓量測量；S1為根節點所在電壓等級對應的系統短路容量；j為虛數單位。

在公共連接點處，由于系統短路容量遠大于負荷容量，線性負荷導納遠小于系統等效導納，可忽略線性負荷導納，得到近似的節點導納矩陣為

式中：n為節點總數；Ypp），且Ypm=Ymp。

可證明對應阻抗矩陣Z的首行首列元素均為xk，且當Y（i，j）=0時，有

式中，（i，j）表示矩陣第i行、第j列元素。

通過比例系數矩陣d，恢復幅值計算式分別為

式中：Aamp為恢復幅值的混合矩陣；分別為恢復了幅值的諧波電流快波動分量和慢波動分量，將其與快波動分量相加即可得到諧波電流的實際值Iamp。

3　IEEE33節點配電網絡驗證

本文算法采用IEEE 33節點標準配電網絡進行驗證，配電網絡如圖1所示。

圖1　IEEE 33節點配電網絡Fig.1　IEEE 33-bus distribution network

在節點20和27處接入諧波源，諧波源地理和電氣距離均相距較遠，符合電網實際情況［19］。諧波電流采用5次諧波典型曲線［9］。在各電流曲線上添加均值為0，方差為0.002的拉普拉斯分布的隨機變量，模擬注入電網的諧波電流。

在電壓量測量上添加均值為0，方差為0.04的高斯白噪聲，分別采用VBICA算法和傳統ICA算法估計諧波電流，并按本文方法恢復諧波電流的次序和幅值，估計結果如圖2所示。由圖2可看出，在噪聲干擾情況下，傳統ICA的估計結果與真實電流曲線差別較大，而VBICA可有效估計諧波電流，得到準確的諧波電流變化曲線。

圖2　5次諧波電流估計結果Fig.2　Estimated results of the 5thharmonic current

工程中常用平均值和95%概率值表征諧波電流的大小，表1給出了諧波電流統計值。由誤差分析結果可看出，相比于傳統ICA算法，VBICA算法極大的降低了估計誤差，驗證了VBICA算法的有效性。

表1　5次諧波電流統計值Tab.1　Statistical values of the 5thharmonic current

4　結語

傳統獨立分量分析算法的估計結果受噪聲影響較大，本文采用變分貝葉斯獨立分量分析進行配電網諧波狀態估計，利用變分貝葉斯理論計算獨立分量分析模型中的未知參數和潛在變量的后驗概率分布，可直接將諧波電流從含噪聲干擾的量測量中提取出來。再結合負荷側等效導納遠小于系統側等效導納的特點，計算諧波電流的幅值。通過IEEE 33節點配網的仿真結果表明，該算法優于傳統獨立分量分析算法，尤其在受到較大噪聲干擾的情況下，該算法估計誤差明顯低于傳統算法，可準確得到諧波電流的波動情況以及統計值，具有重要的工程應用價值。

［1］陸志剛，王科，董旭柱，等（Lu Zhigang，Wang Ke，Dong Xuzhu，et al）.分布式發電對配電網影響分析（Impact of consumer-side distributed generation on power grid）［J］.電力系統及其自動化學報（Proceedings of the CSUEPSA），2012，24（6）：100-106.

［2］李正明，徐敏，潘天紅，等（Li Zhengming，Xu Min，Pan Tianhong，et al）.基于小波變換和HHT的分布式并網系統諧波檢測方法（A harmonic detection method for distributed connected grid system byusing wavelet transform and HHT）［J］.電力系統保護與控制（Power System Protection and Control），2014，42（4）：34-39.

［3］張哲，陳紅坤（Zhang Zhe，Chen Hongkun）.諧波源辨識研究的現狀和發展（Status and development of harmon?ic source identification）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2005，17（5）：37-41.

［4］Heydt G T.Identification of harmonic sources by a state estimation technique［J］.IEEE Trans on Power Delivery，1989，4（1）：569-576.

［5］Van Long Pham，Kit Po Wong，Watson N，et al.A method of utilising non-source measurements for harmonic state estimation［J］.Electric Power Systems Research，2000，56 （3）：231-241.

［6］吳篤貴，徐政（Wu Dugui，Xu Zheng）.基于相量量測的電力系統諧波狀態估計（I）——理論、模型與求解算法（Power system harmonic state estimation based on phasor measurements（I））［J］.電工技術學報（Transac?tions of China Electrotechnical Society），2004，19（2）：64-68，88.

［7］ Liao Huaiwei.Power system harmonic state estimation and observability analysis via sparsity maximization［J］. IEEE Trans on Power Systems，2007，22（1）：15-23.

［8］ 王文生，王進，王科文（Wang Wensheng，Wang Jin，Wang Kewen）.SOM神經網絡和C-均值法在負荷分類中的應用（Application of SOM neural network and Cmeans method in load classification）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2011，23 （4）：36-39.

［9］Gursoy E，Niebur D.Harmonic load identification using complex independent component analysis［J］.IEEE Trans on Power Delivery，2009，24（1）：285-292.

［10］Liao Huaiwei，Niebur Dagmar.Load profile estimation in electric transmission networks using independent compo?nent analysis［J］.IEEE Trans on Power Systems，2003，18 （2）：707-715.

［11］張晶瑩（Zhang Jingying）.獨立分量分析在電力系統諧波電流估計中的應用（Independent Component Analy?sis Applying to Electric Power Harmonic Current Estima?tion）［D］.哈爾濱：哈爾濱工業大學電氣工程及自動化學院，（Harebin：School of Electrical Engineering and Automation of Harbin Institute of Technology），2010.

［12］鄭東方，陳紅坤，楊志平（Zheng Dongfang，Chen Hong?kun，Yang Zhiping）.獨立分量分析在諧波源辨識中的應用（Application of independent component analysis on harmonic source identification）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2012，24（4）：139-144.

［13］張金霞（Zhang Jinxia）.基于獨立成分分析的諧波檢測（Independent component analysis for harmonic detec?tion）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2007，19（1）：74-78.

［14］楊源，臧天磊，何正友（Yang Yuan，Zang Tianlei，He Zhengyou）.一種諧波阻抗未知條件下的諧波源定位方法（A harmonic source location method under un?known harmonic impedance）［J］.電網技術（Power Sys?tem Technology），2014，38（1）：222-226.

［15］孫斌，姚海濤，李田，等（Sun Bin，Yao Haitao，Li Tian，et al）.基于Fast ICA和改進LSSVM的短期風速預測（Short-term wind speed forecasting based on fast ICA al?gorithm and improved LSSVM model）［J］.電力系統及其自動化學報（Proceedings of the CSU-EPSA），2014，26 （1）：22-27.

［16］李洪，孫云蓮（Li Hong，Sun Yunlian）.基于獨立分量分析的局部放電脈沖信號提取（Extraction of partial dis?charge signals using independent component analysis）［J］.電力系統及其自動化學報（Proceedings of the CSUEPSA），2007，19（2）：78-81，107.

［17］范濤，李志農，盧紀富，等（Fan Tao，Li Zhinong，Lu Jifu，et al）.基于變分貝葉斯獨立分量分析的故障源盲分離（Blind separation of fault sources based on variational Bayesian independent component analysis）［J］.噪聲與振動控制（Noise and Vibration Control），2010（1）：82-85.

［18］Novey M，Adali T.Complex ICA by negentropy maximiza?tion［J］.IEEE Trans on Neural Networks，2008，19（4）：596-609.

［19］惠錦，楊洪耕，葉茂清（Hui Jin，Yang Honggeng，Ye Maoqing）.多諧波源條件下的諧波污染責任劃分研究（Research on the responsibility partition of harmonic pol?lution of multiple harmonic sources）［J］.中國電機工程學報（Proceedings of the CSEE），2011，31（13）：48-54.

Harmonic State Estimation Based on Variational Bayesian Independent Component Analysis

HAN Fei，YANG Honggeng，WANG Jiaxing，WANG Ze
（School of Electrical Engineering and Information，Sichuan University，Chengdu 610065，China）

In order to solve the problems that the harmonic impedance is difficult to be obtained accurately，and the measurement noise is unavoidable in practical power system，a harmonic state estimation method based on variational bayesian independent component analysis（VBICA）is proposed.Regarding the harmonic impedance and measurement noise as unknown variables，the posterior probability distributions of unknown variables and latent harmonic current in independent component analysis are calculated by variational Bayesian，and then the optimal harmonic current can be extracted without noise interference through iterative learning.Considering that the admittance of load side is much less than that of system side，the amplitude ratios are derived，and then the amplitude of harmonic current can be comput?ed.The characteristics of the presented method are verified by utilizing the IEEE 33-bus distribution network，also com?pared with conventional independent component analysis method.Experimental results show that the proposed method has higher estimation precision and stronger anti-noise ability.

harmonic state estimation；variational Bayesian；independent component analysis；unknown harmonic im?pedance；noise interference

TM711

A

1003-8930（2016）04-0068-05

2014-06-07；

2015-05-11

韓斐（1989—），女，碩士研究生，研究方向為電能質量、諧波狀態估計。Email：hanfei_1211@163.com

楊洪耕（1949—），男，博士，教授，研究方向為電能質量、無功電壓控制、智能電網等方面的教學和科研工作。Email：pqlab99@126.com

王佳興（1989—），男，碩士研究生，研究方向為電能質量、電壓暫降狀態估計。Email：953249707@qq.com