確界定義的幾種等價(jià)形式
趙 正 波
(渭南師范學(xué)院 數(shù)理學(xué)院,陜西 渭南 714099)
?
確界定義的幾種等價(jià)形式
趙 正 波
(渭南師范學(xué)院 數(shù)理學(xué)院,陜西 渭南 714099)
摘要:給出了確界定義的一個(gè)新的定義形式,建立了確界的直觀語言性定義和形式化定義之間的關(guān)系,指出了已有定義之間的等價(jià)關(guān)系。通過引入函數(shù)確界和多元函數(shù)的點(diǎn)趨于無窮時(shí)的極限概念和應(yīng)用,把確界概念直接應(yīng)用于函數(shù)最值的討論。這個(gè)定義與代數(shù)中確界概念的定義也是相通的,加強(qiáng)了確界概念的普遍性和應(yīng)用之間的關(guān)系。
關(guān)鍵詞:確界;函數(shù)確界;極值;最值
確界概念是關(guān)于實(shí)數(shù)完備性的基本概念,在數(shù)學(xué)分析中有著廣泛的應(yīng)用[1-3]。但是確界概念和直觀理解之間仍然缺乏有效的聯(lián)系,為此我們針對(duì)概念的幾種等價(jià)形式進(jìn)行討論,有助于對(duì)概念的直觀理解和應(yīng)用[4],并且溝通其與現(xiàn)在相當(dāng)廣泛的偏序集上確界概念的聯(lián)系和共性。我們按照概念的層次重新給出確界及其相關(guān)概念的定義,這些有助于我們把數(shù)學(xué)分析和高等數(shù)學(xué)中的有關(guān)界的概念統(tǒng)一起來。
1 實(shí)數(shù)集上確界的概念
有關(guān)實(shí)數(shù)、極限的概念及其性質(zhì)等這里不再一一敘述,相關(guān)的概念可以參閱文獻(xiàn)[1-2]。我們直接在實(shí)數(shù)集上建立界和確界的相關(guān)概念。先看實(shí)數(shù)集上界的定義。
定義1設(shè)S是非空實(shí)數(shù)集,M,L是實(shí)數(shù),
(1)若S中所有的元素都小于或等于M,即?x∈S,x≤M,則稱M是S的上界;
(2)若S中所有的元素都大于或等于L,即?x∈S,x≥L,則稱L是S的下界;
(3)若S中有元素大于M,即?x∈S,x>M,則稱M不是S的上界;
(4)若S中有元素小于L,即?x∈S,x 顯然,上界和不是上界的概念是對(duì)立的并且是排中的,下界和不是下界的概念也是對(duì)立的并且是排中的。上界和下界統(tǒng)稱為界。接下來我們給出實(shí)數(shù)集有界的概念。 定義2設(shè)S是非空實(shí)數(shù)集, (1)若存在實(shí)數(shù)M是S的上界,即?M∈R滿足:?x∈S,x≤M,則稱S有上界; (2)若存在實(shí)數(shù)L是S的下界,即?L∈R滿足:?x∈S,x≥L,則稱S有下界; (3)若任何實(shí)數(shù)都不是S的上界,即對(duì)?M,?x∈S,x>M,則稱S無上界; (4)若任何實(shí)數(shù)都不是S的下界,即對(duì)?L,?x∈S,x (6)若S無上界或者無下界,則稱S無界。 從實(shí)數(shù)集S有上界的定義可以看出,若實(shí)數(shù)集S有上界,則S有無限多個(gè)上界;若實(shí)數(shù)集S有下界,則S有無限多個(gè)下界。并且有如下引理: 引理1[1]設(shè)S是非空實(shí)數(shù)集,若S有上界,則S有最小上界;若S有下界,則S有最大下界。 我們把S的最小上界稱為S的上確界,把S的最大下界稱為S的下確界。 定義3設(shè)S是非空實(shí)數(shù)集, (1)若實(shí)數(shù)ξ滿足兩條:i)?x∈S,x≤ξ;ii)若M是S的上界,則ξ≤M,則稱ξ是S的上確界,記作ξ=supS; (2)若實(shí)數(shù)η滿足兩條:i)?x∈S,x≥η;ii)若L是S的下界,則L≤η,則稱η是S的下確界,記作η=infS; (3)若S無上界,則稱S的上確界是+,記作supS=+; (4)若S無下界,則稱S的下確界是-,記作infS=-。 定義3′設(shè)S是非空實(shí)數(shù)集, (1)若實(shí)數(shù)ξ滿足兩條:i)?x∈S,x≤ξ;ii)若M<ξ,則存在x∈S使得x>M,則稱ξ是S的上確界,記作ξ=supS; (2)若實(shí)數(shù)η滿足兩條:i)?x∈S,x≥η;ii)若L>η,則存在x∈S使得x (3)若S無上界,則稱S的上確界是+,記作supS=+; (4)若S無下界,則稱S的下確界是-,記作infS=-。 在應(yīng)用中,常常把定義中的M寫成ξ-ε,把定義中L寫成η+ε,其中ε表示任何一個(gè)正數(shù),常常理解為任意小的一個(gè)正數(shù),可以對(duì)ε作適當(dāng)限定。這樣使得定義更加直觀,因而也把定義寫成如下形式。 定義3″設(shè)S是非空實(shí)數(shù)集, (1)若實(shí)數(shù)ξ滿足兩條:i)?x∈S,x≤ξ;ii)?ε>0,存在x∈S使得x>ξ-ε,則稱ξ是S的上確界,記作ξ=supS; (2)若實(shí)數(shù)η滿足兩條:i)?x∈S,x≥η;ii)?ε>0,存在x∈S使得x<η+ε,則稱η是S的下確界,記作η=infS; (3)若S無上界,則稱S的上確界是+,記作supS=+; (4)若S無下界,則稱S的下確界是-,記作infS=-。 定義3°設(shè)S是非空實(shí)數(shù)集, 上確界和下確界統(tǒng)稱為確界。我們對(duì)上述4個(gè)定義中關(guān)于上確界定義的第二個(gè)條件之間的關(guān)系進(jìn)行討論。在定義3和定義3′之間,因?yàn)橛小叭鬗是S的上界,則ξ≤M”等價(jià)于逆否命題“若M<ξ,則M不是S的上界”,再由不是上界的概念等價(jià)于“若M<ξ,則存在x∈S使得x>M”,這就說明了定義3和定義3′的上確界的定義第二條是等價(jià)的,因而定義3和定義3′的上確界的定義是等價(jià)的。又由于任意小于ξ的實(shí)數(shù)M,總可以寫成ξ減去某個(gè)正數(shù)ε,而ξ減去任意正數(shù)ε總可以用小于ξ的正數(shù)M來表示,所以定義3′和定義3″的上確界定義中第二條也是等價(jià)的,因而定義3′和定義3″中上確界的兩個(gè)定義是等價(jià)的。只要把定義3″中的ε看成數(shù)列定義中的任意正數(shù)ε,定義3″和定義3°的上確界中關(guān)于上確界的第二條等價(jià)是顯然的,因而定義3″和定義3°的上確界的定義是等價(jià)的,所以關(guān)于上確界的4個(gè)定義是等價(jià)的。同樣可以證明下確界的4個(gè)定義是等價(jià)的。這就完成了4個(gè)定義等價(jià)的證明。應(yīng)用中可選擇4個(gè)定義之一直接引用。 關(guān)于確界的存在和有界的等價(jià)問題,在一般的高等數(shù)學(xué)和數(shù)學(xué)分析教材中都有引理1,我們不再論證,對(duì)于確界的概念首先遇到的是和最值概念之間的關(guān)系,而確界和最值的區(qū)別是其是否屬于集合。 定理1設(shè)S為非空集,則 (1)supS=ξ∈S?ξ=maxS; (2)infS=η∈S?η=minS。 由確界的概念與極限的概念的獨(dú)立性可知,可以用其中一個(gè)概念去計(jì)算另外一個(gè)概念,給確界的判定和確界概念的應(yīng)用帶來極大方便。而定義3是直觀性和數(shù)學(xué)本質(zhì)之間聯(lián)系的橋梁,也給我們把確界的概念推廣到一般的偏序集上帶來了方便。 由于極限的運(yùn)算法則和確界的概念是獨(dú)立的,利用確界和極限的關(guān)系,應(yīng)用極限的四則運(yùn)算和不等式的性質(zhì)容易得到以下結(jié)論: 定理2設(shè)A,B為非空集,若?x∈A和?y∈B有x≤y,則supA≤infB。 推論1設(shè)A,B為非空集,且S=A∩B非空,則 (1)supS≥max{supA,supB}; (2)infS≤min{infA,infB}。 定理3設(shè)A,B為非空集,S=A∪B,則 (1)supS=max{supA,supB}; (2)infS=min{infA,infB}。 (1)supS-=-infS; (2)infS-=-supS。 (1)sup(A+B)=supA+supB; (2)inf(A+B)=infA+infB。 (1)sup(A·B)=supA·supB; (2)inf(A·B)=infA·infB。 定理7設(shè)函數(shù)y=f(P),P∈D,在D內(nèi)有有限個(gè)極值點(diǎn)f(P1),f(P2),…,f(Pn),邊界點(diǎn)有相同的極限ξ,或無窮遠(yuǎn)處有相同的極限η,則 (1)supf(P)=max{f(P1),f(P2),…,f(Pn),ξ,η}; (2)inff(P)=min{f(P1),f(P2),…,f(Pn),ξ,η}。 例1證明圓的所有外切三角形中,正三角形的面積最小。 例4(水箱設(shè)計(jì)問題)要設(shè)計(jì)一個(gè)容積為V的長方體開口水箱,試問水箱的長寬高各等于多少時(shí),其表面積最小? 在一般的偏序集上,我們同樣可以定義界和確界的相關(guān)概念。例如有界的定義如下[3],其他的概念有類似的定義。 定義4設(shè)(P,≤)為偏序集,S?P是非空集,M,L∈P, (1)若S中所有的元素都小于或等于M,即?x∈S,x≤M,則稱M是S的上界; (2)若S中所有的元素都大于或等于L,即?x∈S,x≥L,則稱L是S的下界; (3)若S中有元素大于M,即?x∈S,有x>M,則稱M不是S的上界; (4)若S中有元素大L,即?x∈S,有x 我們把定義3直接推廣到偏序集上,這樣就得到更一般的偏序集上確界的定義,這樣的定義本質(zhì)上是代數(shù)形式的定義。 定義5設(shè)(P,≤)為偏序集,S?P是非空集,ξ,η∈P, (1)若ξ滿足兩條:i)?x∈S,x≤ξ;ii)若M是S的上界,則ξ≤M,則稱ξ是S的上確界,記作ξ=supS; (2)若η滿足兩條:i)?x∈S,x≥η;ii)若L是S的下界,則L≤η,則稱η是S的下確界,記作η=infS。 確界是數(shù)學(xué)中應(yīng)用非常廣泛的概念之一,我們還可以得到更強(qiáng)條件下確界的判定條件。但是作為等價(jià)形式把這個(gè)概念建立成統(tǒng)一的形式有著積極的意義,其他學(xué)科上的確界概念都是偏序集上確界概念的應(yīng)用,我們把實(shí)數(shù)集的確界概念也歸入這個(gè)形式,并且深化了它的應(yīng)用。 參考文獻(xiàn): [1] 華東師范大學(xué)數(shù)學(xué)系.數(shù)學(xué)分析[M].北京:高等教育出版社,2008. [2] 劉三陽,李廣民.數(shù)學(xué)分析十講[M].北京:科學(xué)出版社,2011. [3] 王國俊.數(shù)理邏輯引論與歸結(jié)原理[M].第2版.北京:科學(xué)出版社,2006. [4] 趙正波.函數(shù)的確界和應(yīng)用[J].渭南師范學(xué)院學(xué)報(bào),2015,30(22):25-27. 【責(zé)任編輯牛懷崗】 中圖分類號(hào):O172.1 文獻(xiàn)標(biāo)志碼:A 文章編號(hào):1009-5128(2016)16-0024-05 收稿日期:2016-04-25 基金項(xiàng)目:渭南師范學(xué)院(省)扶持學(xué)科數(shù)學(xué)學(xué)科基金資助項(xiàng)目:模糊謂詞演算系統(tǒng)的研究(14SXZD006) 作者簡(jiǎn)介:趙正波(1966—),男,陜西渭南人,渭南師范學(xué)院數(shù)理學(xué)院講師,理學(xué)碩士,主要從事非經(jīng)典邏輯研究。 Supremum and Infimum and Its Equivalent Propositions ZHAO Zheng-bo (School of Mathematics and Physics, Weinan Normal University, Weinan 714099, China) Abstract:It has introduced a new proposition of supremum and infimum, which gives the relation between intuition and formalization proposition. It has gotten out directly application on solving maximum and minimum of function by introducing supremum and infimum of function of multivariate function among extrema and limits as point P approaches infinity or borders which is not in domain. It has also given out extensive proposition of supremum and infimum on partially ordered set. Key word:supremum and infimum; supremum and infimum of function; extrema; maximum and minimum 【自然科學(xué)基礎(chǔ)理論研究】
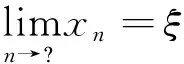
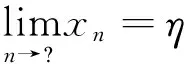
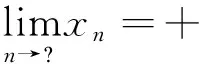
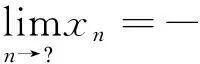
2 實(shí)數(shù)集上確界的性質(zhì)
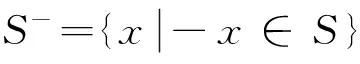
3 函數(shù)的確界及其應(yīng)用
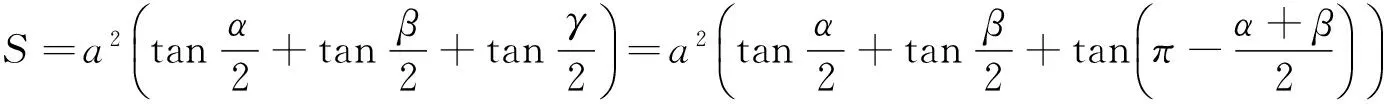
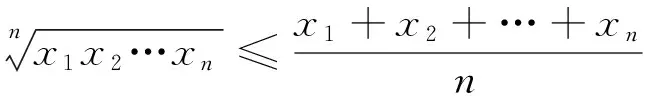
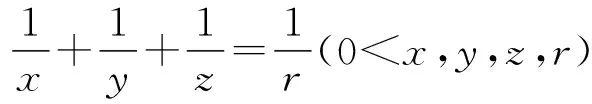
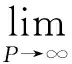
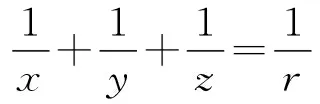
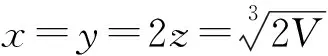
4 有序集上的確界
5 結(jié)語

